Rep:Transition States and Reactivity ZWL115
Introduction
What is a potential energy surface?
A potential energy surface (PES) describes the potential energy of a chemical system in terms of certain parameters such as time and extent of reactions. Each geometry of the atoms in a system has its own unique potential energy due to the varying distances of the different atoms. Two atoms which are very far apart will have no interactions while 2 atoms which are very close together will have strong repulsive forces between them. This results in the creation of a smooth energy landscape such as the one shown in Figure 1. In Figure 1, the vertical coordinate gives the potential energy which varies with the 2 horizontal coordinates which are the bond lengths of atoms AB and atoms BC

What is a transition state?
Minima in a PES are assiociated with the structures of the reactants, products or intermediates of a reaction system. The reaction path is the lowest energy pathway between the reactant minimum and the product minimum which is denoted as a red line in Figure 1. The highest point on the reaction path corresponds to the transition state. A minimum and a transition state are both stationary points as they have zero gradient on the PES. For a stationary point, the Hessian Index, which is the number of negative eigenvalues of a force constant matrix, corresponds to the number of internal degrees of freedom along which that point is a potential energy maximum2. The Hessian Index is also equal to the number of imaginary vibrational frequencies. A minimum and a transition state can be distinguished via this Hessian Index. A minimum will have only positive eigenvalues of the Hessian and have an Hessian Index of 0. Hence, there will be no imaginary frequencies. However, since a transition state is the maximum of the lowest energy pathway, it will have a single negative Hessian eigenvalue and have a Hessian Index of 0. Hence, it will have a single imaginary vibrational frequency.
Nf710 (talk) 10:58, 9 March 2018 (UTC) Good understanding of the Hessian Matrix. The eigenvectors are the normal modes which are linear combination of the degrees of freedom and hne you move along these vectors this is what looks like a vibration.
Quantum Chemical methods used
The semi-empirical PM6 method was used for initial calculations, followed by the more accurate DFT (Density Functional Theory) method B3LYP. The PM6 method was used to speed up initial calculations due to the method replacing some of the two-electron integrals, the Coulomb and the exchange integrals (which are difficult to calculate), used in the Hartree Fock, with empirical parameters.3 The DFT method is a computational method that derives the properties of a molecular system based on the determination of the electron density of the molecule.4 Unlike a wavefunction, which becomes increasingly complex as the number of electrons increase, the determination of electron density is independent of the number of electrons. The B3LYP method is a hybrid method which utilises the useful features from ab initio methods and improves the accuracy of the calculation by DFT mathematics. The 6-31G basis set was chosen as a larger basis set gave a better approximation to the atomic orbitals as they placed fewer restrictions on the wavefunction while the split basis sets allowed for size changes during bonding.5
Nf710 (talk) 10:58, 9 March 2018 (UTC) Good understanding here you have clearly read beyond the script here. Some equations would have been nice to back up your arguements.
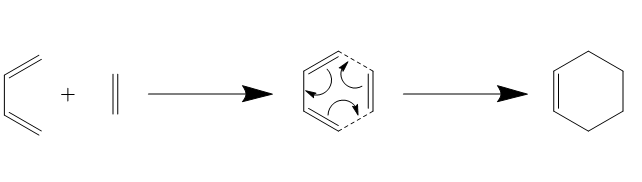
Exercise 1: Reaction of Butadiene and Ethene
(Fv611 (talk) Very good work across the whole exercise. Only hiccups is your discussion of the bond lengths: the VdW distance between two atoms is the sum of their VdW radius, so at the TS the terminal carbons are starting to bond.)
Reaction Scheme
Jmol Files
| Butadiene | Ethene | Transition State | Cyclohexene | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
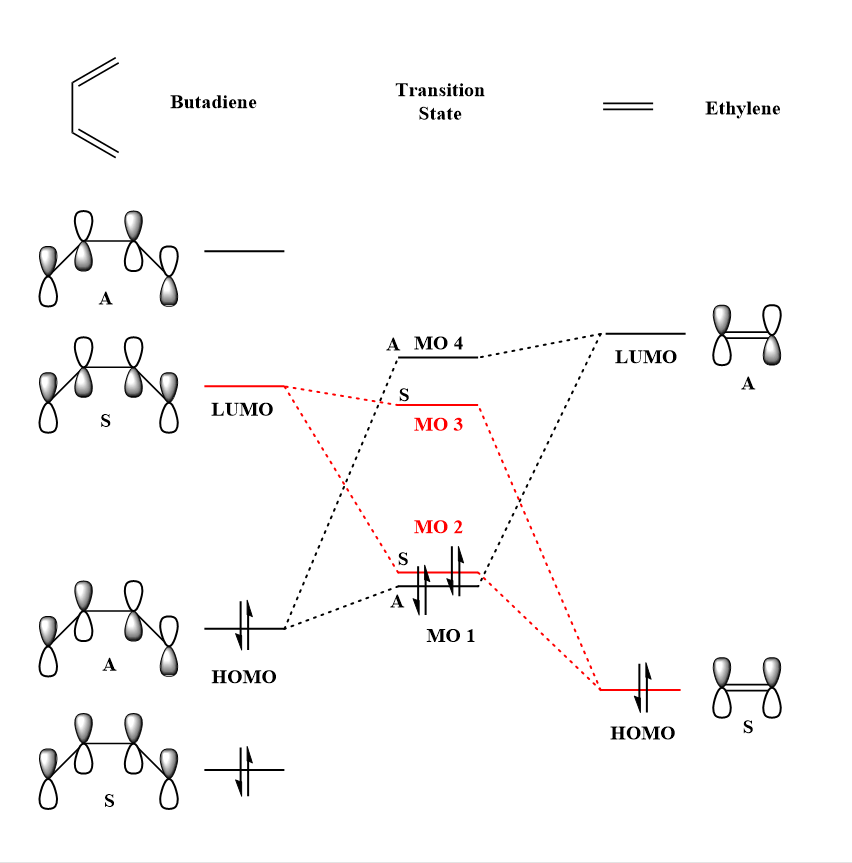
MO Diagram
| Butadiene | MO diagram for the formation of the Butadiene/Ethene transition state | Ethene | ||||
|---|---|---|---|---|---|---|
 |
||||||
| MO 1 | MO 2 | MO 3 | MO 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
Referring to the MO diagram above, the HOMO of butadiene is higher in energy than that of ethene, indicating that this is a normal electron demand cycloaddition. Bonding MOs (MOs 1 and 2) of the transition state formed from the MOs of the reactants are much higher in energy than what is expected for a product. Similarly, the anti-bonding MOs of the transition state are lower in energy than the corresponding MOs of the product. This is due to the fact that the transition state lies at the maximum of the lowest energy pathway and the overlap of orbitals are not as strong as what would be seen in the products of the reaction. This leads to an overall destabilisation of the structure as the electrons are occupying MOs which are higher in energy than that of the reactants.
Symmetry
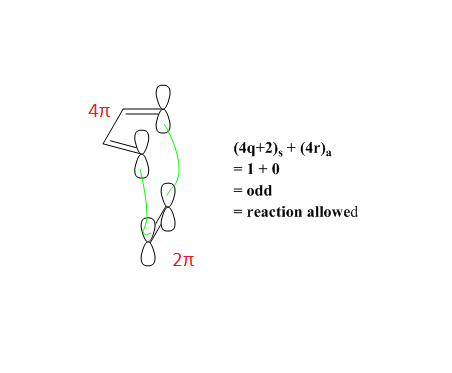
For a thermal pericyclic reaction, whether a reaction is 'allowed' or 'forbidden' depends on the Woodward-Hoffmann rules which states that the total number of (4q+2)s and (4r)a components must be odd.6 The suffix 's' represents suprafacial where the new bonds are formed on the same side at both ends of the component. The suffix 'a' represents antarafacial where the new bonds formed are on opposite sides of both ends of the component. As seen from Figure 2, when both components are suprafacial, it would allow for good orbital overlap and the Woodward-Hoffmann rules are obeyed. This is in agreement with the results obtained for the combination of the Frontier Orbitals of butadiene and ethene in the MO diagram. Reactions are only allowed when the symmetry of the FO of butadiene is the same as that for the FO of ethene as this would lead to a non-zero orbital overlap. Conversely, an overlap between a symmetric FO and an anti-symmetric FO would lead to an orbital overlap integral of 0 and hence, no reaction will occur.
Bond Length Analysis
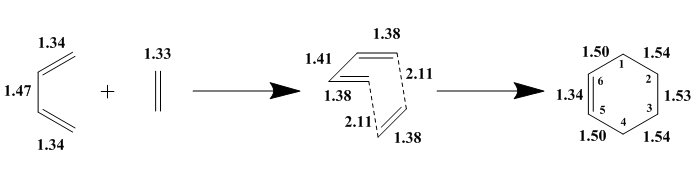
The C-C bond lengths for the reactants, transition state and the products are summarised in the Figure 3. Butadiene has shorter C=C terminal bonds of 1.34 Å and a longer C-C internal bond of 1.47 Å while ethene has a bond length of 1.33 Å. The shorter bond lengths observed in butadiene are due to the overlap between sp2 C atoms which have a typical value of 1.34 Å7 while the longer C-C bonds observed are due to the overlap between sp3 C atoms which have a typical value of 1.54 Å.7 At the transition state, the C=C terminal bonds of butadiene and the C=C bond in ethene lengthen to 1.38 Å, moving towards the value of a bond length observed between sp3 C atoms. This indicates that the bond order has decreased from 2 to a value between 1 and 2. In contrast, the internal bond shortens to 1.41 Å, moving towards the value of a bond length observed between sp2 C atoms and the bond order has increased from 1 to a value between 1 and 2, similar to the bond lengths of the terminal bonds. Finally in the products, the bond lengths continue to change in the same way. C5-C6 which was previously the internal bond of the butadiene has the shortest bond length of 1.34 Å due to the overlap between sp2 C atoms. C1-C2, C2-C3 and C3-C4 have very similar bond lengths of 1.53-1.54 Å which reflects the overlap between sp3 C atoms. C1-C6 and C4-C5 which were previously the terminal bonds of the butadiene have a bond length of 1.50 Å which is slightly shorter than the other single bonds in the molecule. This is due to the sp2-sp3 overlap of the C atoms. The greater s character of the sp2 C atom results in a stronger and shorter sigma bond. The length of the partially formed C-C bonds in the transition state is 2.11 Å which is significantly greater than the Van Der Waals radius of C (1.70 Å).8 This indicates that at the transition state, no new C-C bonds were formed.
Reaction path towards the products from the transition state
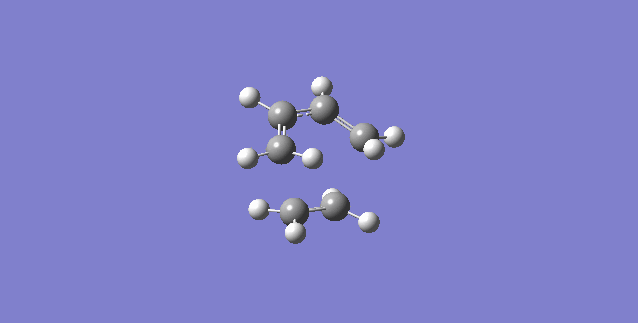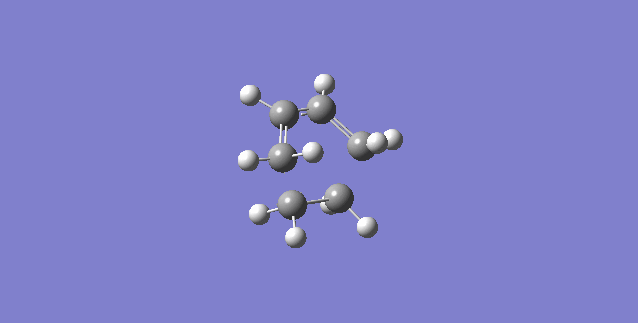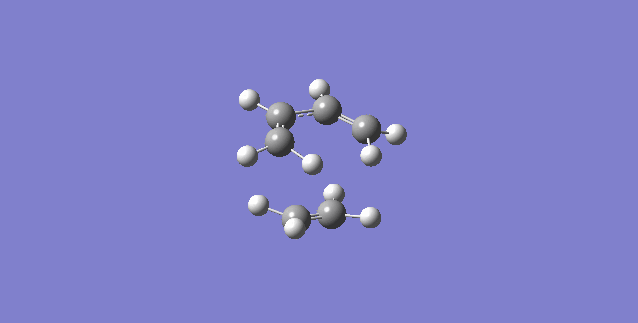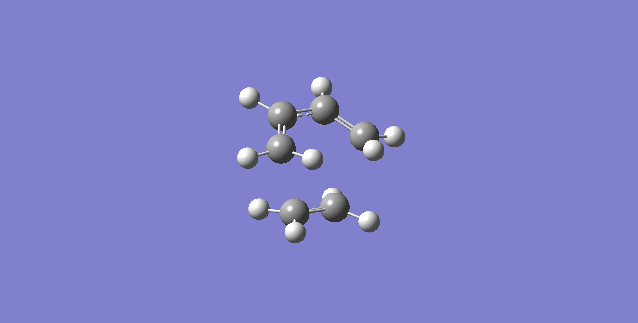
As seen from the illustration showing the vibration corresponding to the transition state, the formation of the 2 bonds is synchronous. The ends of the butadiene and ethene fragments move towards each other in a symmetric fashion showing a concerted mechanism.
Link to Exercise 2
https://wiki.ch.ic.ac.uk/wiki/index.php?title=Transition_States_and_Reactivity_Exercise2_ZWL115
Link to Exercise 3
https://wiki.ch.ic.ac.uk/wiki/index.php?title=Transition_States_and_Reactivity_Exercise3_ZWL115
Conclusion
The use of the semi-empirical method PM6, followed by the DFT method B3LYP has provided the tools required to locate the transition states for several reactions, allowing great insight into the nature of the reactions. Following a successful vibration calculation, an IRC can be carried out to ensure that the minima of the reactants and the products were reached and were connected. In Exercise 1, the energy levels of the individual MOs of the reactants, transition states and the products were obtained, allowing for the construction of the MO diagram which was useful in studying the symmetry of the 'allowed' and 'forbidden' reactions. Exercise 2 involved an inverse electron demand Diels-Alder reaction due to the different ordering of energies of the HOMO and LUMO of the dienophile and the diene as compared to Exercise 1. This allowed for the comparison between the MO diagrams of a normal versus an inverse electron demand Diels-Alder. It was found that the MO diagrams for the 2 reactions had similar relative energy levels for their respective transition states. The study of the reaction thermodynamics in Exercises 2 and 3 confirmed the role of steric clashes and secondary orbital interactions in determining which transition states and products are favourable and vice versa. Steric clashes raised the energy of the compound while secondary orbital interactions helped to lower the energy of the chemical system. Exercise 3 also showed the role of aromaticity in providing stability to a molecule and lowering its energy while anti-aromatic compounds are highly unstable.
References
1. Potential Energy Surface. Encyclopedia of Human thermodynamics.
2. Potential Energy Surfaces. C, David Sherrill. School of Chemistry and Biochemistry Georgia Institute of Technology.
3. Computational Quantum Chemistry. C, David Sherrill.
4. Introduction to Computational Quantum Chemistry: Theory. A, Gilbert. The Australian National University.
5. Introduction to Computational Chemistry. V H¨anninen. University of Helsinki
6. Woodward, R. B.; Hoffmann, R. J. Am. Chem. Soc. 1965, 87(2), 395-397.
7. Bond Length. Wikipedia.
8. Van der Waals radius. Wikipedia.
(Fv611 (talk) Wikipedia IS NOT an acceptable primary source. Any inorganic textbook would have done here.)