Rep:TransitionStates-HYT215

Introduction

The potential energy surface (PES) represents the potential energy of the molecule visualised along two dimensions. The potential energy is a function of 3N-6 independent nuclear coordinates where $E=f(q_1,q_2,q_3,...,q_{3N-6})$. If the energy is plotted only along one dimension, an energy profile is obtained. This can also be obtained by taking a vertical slice of the PES. When the first derivative of the PES is zero $(\frac{\partial E(q_1)}{\partial q_1}=0)$, it corresponds to a minimum, maximum or saddle point. To better understand the nature of these points, the second derivative $(\frac{\partial E^2}{\partial q_1^2})$, corresponding to the frequency is calculated. If this value is positive, it is the minimum of the PES. This typically corresponds to reactant or products. If the value is negative, it could be a saddle point which corresponds to the transition state of a molecule. As the bonds can be approximated to a harmonic oscillator, it obeys Hooke's law where:

Nf710 (talk) 00:22, 17 November 2017 (UTC)This is good bit not quite correct. Minimum all 3n-6 dimensions second derivatives positive. TS - all 3n-6 dimensions second derivatives positive apart from one which is a negative and therefore a maximum which corresponds to the reaction coordinate.

$F=kx$

As the potential energy is work done over distance: $V=\int F\mathrm{d}x$

Therefore: $V=\frac{1}{2}k{x}^2$

$k=\frac{\partial E^2}{\partial q_1^2}$

We can thus solve for the frequency: $\nu =\frac{1}{2\pi }\sqrt{\frac{k}{\mu }}$, where: $\mu =\frac{m_1{m}_2}{m_1+m_2}$

The above calculations are valid due to Born-Oppenheimer approximation, where the electronic distribution of a molecule adjust instantaneously to the movement of a nuclei and that the energy is a function of nuclei positions, where nuclear kinetic energy is not taken into account.

Through Gaussian calculations, the reactants, transition states and products were optimised. All calculations were done at PM6 level except exercise 2 where the optimised PM6 structures were further optimised at B3LYP 6-31G(d) level. From these optimisations, the molecular orbitals, bonds lengths and intrinsic reaction coordinates could be obtained and analysed. The thermodynamic data from Gaussian calculations were also used to support the analysis on competing reactions for Exercise 2, Exercise 3 and the extension.

Nf710 (talk) 00:15, 17 November 2017 (UTC) Great intro. Good understanding of the vibrations. You could have spoke more about the quantum mechanical methods that you have used however.

Exercise 1: Reaction of Butadiene with Ethylene

The Diels-Alder reaction of butadiene with ethylene to give cyclohexene is an example of a Diels-Alder reaction. It is a [4+2] cycloaddition between a conjugated diene (butadiene) and dienophile (ethylene), with the reaction scheme given below.

Reaction scheme of butadiene with ethylene to form cyclohexene

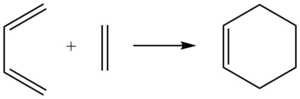
Molecular Orbitals of Transition State

Through computational methods done at PM6 level, the transition states, along with HOMOs and LUMOs of the two reactants were obtained as shown below.

Butadiene		Ethene
Optimised		Optimised
MO 12 (LUMO)		MO 7 (LUMO)
MO 11 (HOMO)		MO 6 (HOMO)

The interaction of the above four MOs during the transition state gave the four MOs below.

Transition State
Optimised	MO 16	MO 17 (HOMO)	MO 18 (LUMO)	MO 19

By observing the interactions of the orbitals and using the relative energy levels found from the calculations, the MO diagram of the transition state is given below. It is also noted that for the orbitals to interact, they must have the same symmetry labels. If not, the reaction would be forbidden.

The antisymmetric HOMO of butadiene (MO 11) interacts with the antisymmetric LUMO of ethylene (MO 7) to give the two antisymmetric MOs, bonding orbital MO 16 and anti-bonding MO 19 of the cyclohexene transition state. The symmetric LUMO of butadiene (MO 12) interacts with the symmetric HOMO of ethylene (MO 6) to give the two symmetric MOs, bonding orbital MO 17 and anti-bonding MO 18 of the cyclohexene transition state.

(Fv611 (talk) Even though your description is right, your MO diagram is wrong! You have drawn the two symmetric orbitals to be a combination of the asymmetric fragment orbitals. A shame because you have drawn the actual MOs correctly and have calculated them well.)

Hence, it is concluded that for a symmetric-symmetric or antisymmetric-antisymmetric interaction, the orbital overlap integral is non-zero. However, a symmetric-antisymmetric interaction would be zero. (Fv611 (talk) Actually the symmetry requirements are a consequence of the value of the orbital overlap rather than viceversa.)

Bond Lengths

	Jmol	Bond Lengths (unit)
Butadiene		C1-C9: 1.33 Å C9-C7: 1.47 Å C7-C4: 1.33 Å
Ethylene		C1-C4: 1.33 Å
Transition State		C1-C9: 1.38 Å C9-C7: 1.41 Å C7-C4: 1.38 Å C4-C14: 2.11 Å C14-C11: 1.38 Å C11-C1: 2.11 Å
Cyclohexene		C3-C4: 1.50 Å C4-C5: 1.34 Å C5-C6: 1.50 Å C6-C1: 1.54 Å C1-C2: 1.53 Å C2-C3: 1.54 Å

The two double bonds of the butadiene increase from 1.33 Å to 1.38 Å in the transition state and then to 1.50 Å in the product. These bonds were initially sp²-sp² C-C double bonds which lengthened to form the sp³-sp² C-C single bonds.

The single bond of butadiene decreased from 1.47 Å to 1.41 Å in the transition state and then to 1.34 Å in the final product. The bond was initially sp²-sp² C-C single bond which shortened to form the sp²-sp² C-C double bond.

The double bond of ethylene increased from 1.33 Å to 1.38 Å in the transition state and then to 1.54 Å in the product. The bond was a sp²-sp² C-C double bond which lengthened to form a sp³-sp³ C-C single bond.

The bond formation between butadiene and ehtylene was reflected in the decrease in the distance of 2.11 Å during the transition state to 1.54 Å in the product, typical of the sp³-sp³ C-C single bond.

It is noted that the lengths of the C-C single bonds are dependent on the amount of s character. The higher the s character of the orbitals, the shorter the bond. The sp³-sp³ C-C single bonds are longer than the are sp³-sp² C-C single bonds, which is also longer than the sp²-sp² C-C single bonds. sp²-sp² carbons with a higher bond order of two has a shorter length than that of one.

The double bonds of butadiene, ethylene and cyclohexene correspond closely to literature values of alkene of 1.34 Å. The sp³-sp² C-C single bond of cyclohexene also corresponds to the literature value of 1.50 Å. The sp²-sp² C-C single bond of butadiene also corresponds to the literature value of 1.47 Å. The sp³-sp³ C-C single bonds of cyclohexene also correspond to the literature value of 1.54 Å. The distance between the two carbons forming the bond of 2.11 Å is smaller than two times the length of the van der Waals radius of carbon (3.4 Å), indicating bond forming or breaking in the transition state.

Reaction Path

The vibration below shows the reaction path at the transition state. As the bond formation between the diene and dienophile took place simultaneously, this bond formation is synchronous.

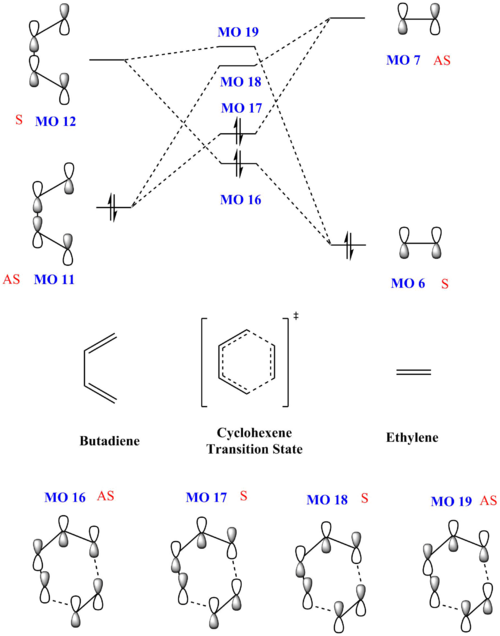
Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Continuing from the previous exercise, this section explores another Diels-Alder between a cyclohexadiene and 1,3-dioxole where dioxole is the dienophile, with the reaction scheme given below. As the dienophile is now substituted, the direction of approach of dioxole would affect the stereochemistry of the product formed, either an endo- or exo- product.

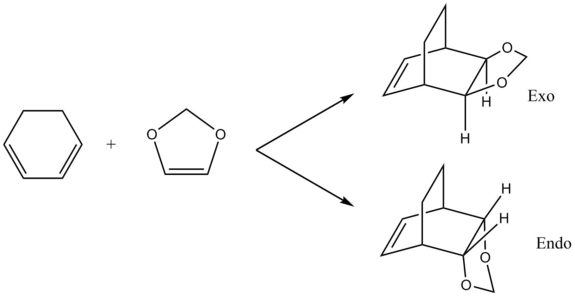
Molecular Orbitals of Transition States

Through computational methods done at B3LYP 6-31G(d) level, the HOMOs and LUMOs of the two reactants were obtained as shown below

1,3-cyclohexadiene		1,3-dioxole
Optimised		Optimised
MO 23 (LUMO)		MO 20 (LUMO)
MO 22 (HOMO)		MO 19 (HOMO)

The interaction of the above four MOs during the transition state for both endo and exo products gave the four MOs below.

Transition States
	Optimised	MO 40	MO 41 (HOMO)	MO 42 (LUMO)	MO 43
Exo
Endo

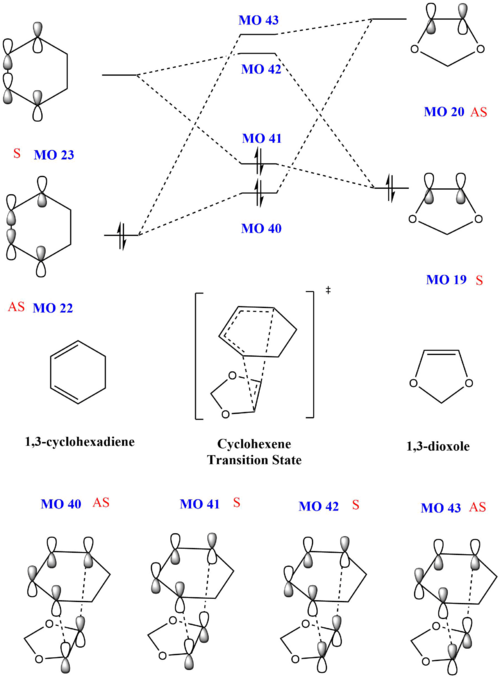
Using the energy levels of MOs derived from the calculations, the following MO diagram was obtained. For a normal Diels-Alder reaction, as shown in exercise 1, the diene is electron rich and has a higher HOMO than the dienophile, which is electron poor. However, in this inverse demand Diels Alder reaction, 1,3-dioxole is an electron rich dienenophile and has a higher HOMO than the cyclohexadiene. This occurs due to the presence of electron rich oxygen atoms adjacent to the C-C double bond on 1,3-dioxole. The electron donating effect of the oxygen atoms lead to 1,3-dioxole having a higher HOMO.

Exo	Endo

Energy Calculations

	Energy/ kJmol-1
1,3-cyclohexadiene	-6.1259 × 105
1,3-dioxole	-7.0119 × 105
Sum of Reactants	-1.3138 × 106

	Energy/ kJmol-1
	Transition State	Product	Reaction Barrier	Reaction Energy
Exo	-1.313614 × 106	-1.313845 × 106	167.71	-63.744
Endo	-1.313621 × 106	-1.313849 × 106	159.88	-67.334

Due to the reaction energy being lower, the endo product is also thermodynamically favoured. Typically, the exo product is thermodynamically preferred as the endo product is likely to have diaxial interactions. However, it is observed that both the exo and endo product have steric clashes.

As the reaction barrier is lower for the endo product, it is kinetically favoured. This is due to secondary interactions between the oxygen atom on the 1,3-dioxole with the 1,3-cyclohexdiene, which will be further elaborated. The HOMO of the transition states were also analysed in greater detail. When the mo cutoff was decrease to 0.01, the interactions for the p-orbitals that were expected from the HOMO (MO 41) of the exo transition state is now clearer as compared to when the isovalue was 0.02 (as seen above). For the HOMO of the endo transition state, there are secondary interactions, further stabilising the transition state, thus lowering its energy. The interactions have now been drawn into the schematic diagram of MO 41 in the table below. These favourable secondary interactions were not observed for the HOMO of the exo transition state. This is probably why the endo product is kinetically favoured over the exo product.

	Exo	Endo
Product
HOMO at isovalue=0.01
Schematic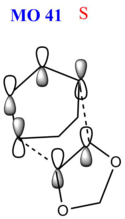

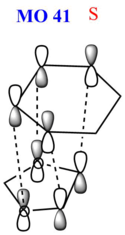Nf710 (talk) 00:21, 17 November 2017 (UTC) Good section. You have explained everything clear and used the diagrams to great effect well done. More understanding of the quantum mechanical methods would have been nice.

Exercise 3: Diels-Alder vs Cheletropic

Similar to exercise 2, the competing reactions between o-xylylene and SO₂ were examined. Firstly, there are two possible Diels-Alder products, endo and exo. Secondly, there is an additional cheletropic reaction that could take place where the sulfur atom forms a five-membered ring with o-xylylene. These products are shown in the scheme below.

Reaction scheme between sulfur dioxide and o-xylylene to give endo and exo Diels Alder as well as cheletropic product

(Oxygen is in the wrong place in the DA products Tam10 (talk) 16:50, 10 November 2017 (UTC))

Optimised Transition States

The transition states were optimised at the PM6 level and are shown below.

	Diels-Alder (Exo)	Diels-Alder (Endo)	Cheletropic
Optimised TS

Energy Calculations and Reaction Profile

The following calculations of the reactants, transition states and products of both exo and endo Diels Alder and chelatropic products were carried out at PM6 level and tabulated below.

	Energy/ kJmol-1
o-Xylylene	469.85
SO2	-311.42
Sum of Reactants	158.43

	Energy/ kJmol-1
	Transition State	Product	Reaction Barrier	Reaction Energy
Exo	241.75	56.330	83.318	-102.10
Endo	237.77	56.976	79.339	-101.46
Cheletropic	260.08	-0.0052510	101.65	-158.44

From the calculations, the reaction profile was derived and plotted on Microsoft Excel.

Reaction profile to of both the endo and exo Diels Alder products and the cheletropic product

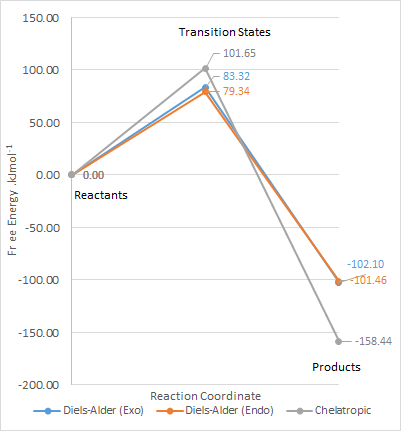
The endo Diels Alder product is kinetically favoured as it has the lowest reaction barrier, probably due favourable seoncdary orbital interactions as discussed above.

The cheletropic product is the most stable and has the lowest reaction energy, and is the thermodynamic product. In the cheletropic form, the molecule is able to adopt a planar configuration, and maximise the distance between the oxygen atoms and the neighbouring hydrogen atoms. It can be seen from the HOMOs below that the Diels Alder products both have some steric clashes, especially with the sulfur the sulfur atom. As sulfur is larger, the anti-bonding interactions of its larger orbitals with surrounding oxygen decreases the stability of the Diels Alder products. There is little favourable bonding bonding interactions. However, the cheletropic HOMO consists of strong bonding interactions between the two pairs of carbons.

	Diels-Alder (Exo)	Diels-Alder (Endo)	Cheletropic
HOMOs of Optimised Products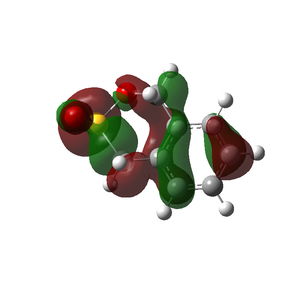

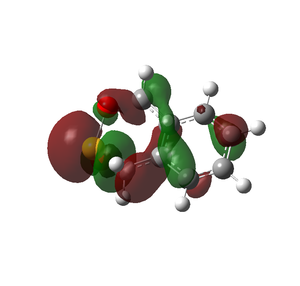
(Nice work. It's quite hard though to draw conclusions from just the HOMO of each, especially at the PM6 level where the MOs have little meaning Tam10 (talk) 16:50, 10 November 2017 (UTC))

IRC

	Diels-Alder (Exo)	Diels-Alder (Endo)	Cheletropic
IRC Coordinates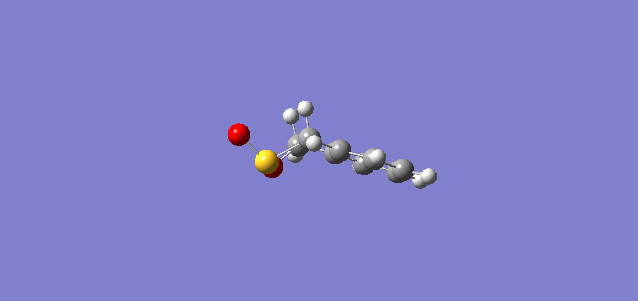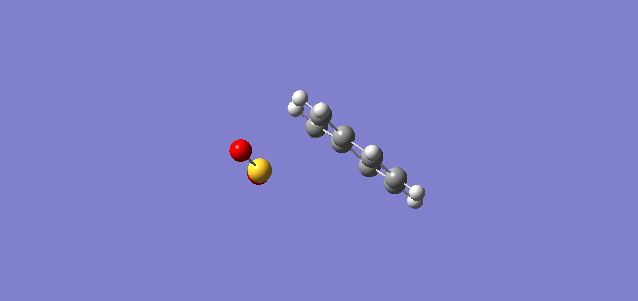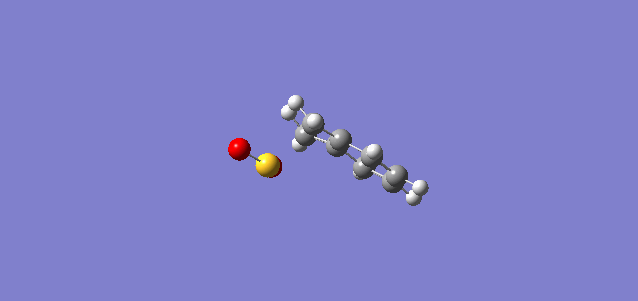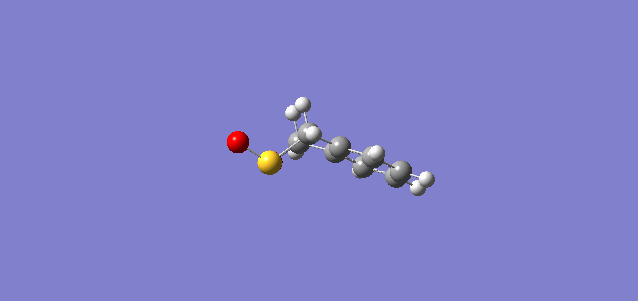
IRC Files	IRC File	IRC File	IRC File

From the IRC shown above, the 6-membered ring of o-xylylene initially consisted of 4 C-C single bonds and 2 C-C double bonds. After the reaction, the 6-membered ring gained stability through aromaticity.

Extension

As o-xylylene contains two diene fragments suitable to undergo a Diels-Alder reaction, this section will move on to explore the reaction profile of this reaction relative to exercise 3. The reaction scheme is shown below.

Reaction scheme of sulfure dioxide undergoing Diels Alder with the second cis-butadiene fragment on o-xylylene

	Diels-Alder (Exo)	Diels-Alder (Endo)
Optimised TS
Optimised Product

(You have the wrong frame for all of these geometries. They are all showing step 14 of the optimisation, not the final geometry Tam10 (talk) 16:51, 10 November 2017 (UTC))

Energy Calculations and Reaction Profile

	Energy/ kJmol-1
o-Xylylene	469.85
SO2	-311.42
Sum of Reactants	158.43

	Energy/ kJmol-1
	Transition State	Product	Reaction Barrier	Reaction Energy
Exo	242.58	176.71	117.39	18.276
Endo	267.98	172.26	109.55	13.829

From the calculations, the reaction profile was derived and plotted on Microsoft Excel.

Reaction profile to of both the endo and exo Diels Alder products of sulfur reacting with the second cis-butadiene fragment

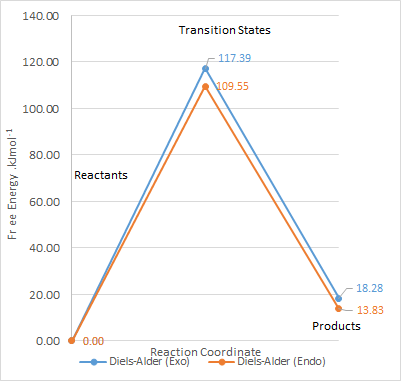
As the activation energy for both the exo and endo product is higher than that of the reaction on the other cis-butadiene fragment site, this site of reaction is less kinetically favourable. The reaction energy is also slightly positive in this case, as compared to negative values in the exercise 3. This shows that the products formed are more unstable than the reactants, and is thermodynamically unstable. By comparing the HOMOs of the products in this exercise to the Diels Alder products of exercise 3, there are even more unfavourable interactions, especially between the carbon atoms. These probably account for the high energy levels of the product.

	Diels-Alder (Exo)	Diels-Alder (Endo)
HOMOs of Optimised Products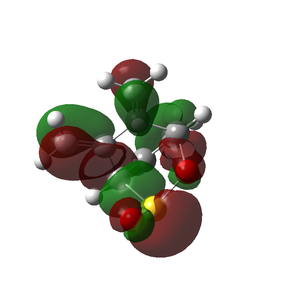

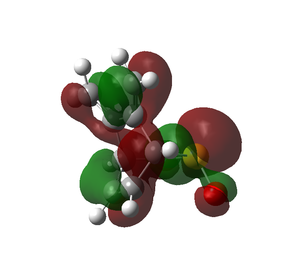
(Nice work. Again, you won't be able to draw too many conclusions from the HOMO of the PM6 calculations Tam10 (talk) 16:52, 10 November 2017 (UTC))

Conclusion

The optimisation and frequency calculations through computational chemistry allowed for the understanding of different reactions. Firstly, the visualisation of MOs of transition state in exercise 1 allowed for the conclusion that interacting MOs must have the same symmetry. The analysis of bond lengths in exercise 1 showed the importance of both hybridisation and bond order. The MO diagram of exercise 2 exemplified an inverse demand Diels Alder reaction, as compared to a normal Diels Alder in exercise 1. In both exercise 2, 3 and the extension, the competing reactions between Diels Alder exo and endo products and cheletropic products were analysed using the energy profile diagram. The importance of sterics and secondary orbital interactions in affecting the kinetic and thermodynamic products were also discussed.