Rep:Tr States:Zm714

Abstract

Computational methods (Semi-Empirical/PM6 and B3LYP/6-31(d)) in Gaussian were used to determine the potential transition state and energies of [4+2] Diels-Alder cycloadditions after optimisation. Reactions between ethene and butadiene, the Endo and Exo reaction energies of 1,3-cyclohexadiene and 1,3-dioxole, and finally comparisons between Diels-Alder and Cheletropic reactions with sulphur dioxide and 5,6-bismethylene-1,3-cyclohexadiene reaction energies and orbitals were investigated.

Introduction

Diels-Alder Reactions

It is well known that [_π4_s+_π2_s] Diels-Alder cycloaddition reactions are fundamental in organic and inorganic chemistry. The symmetry requirements of these reactions have been well researched and their thermodynamic and kinetic reaction dynamics have been well established, particularly in computational methods.

Fig. 1 The orbital interactions of the diene and dienophile.

In order for a successful Diels-Alder reaction to occur, there are strict orbital symmetry rules which must be obeyed. These were explored extensively by Woodward et al and their work in this field led to the development of the Woodward-Hoffmann rules which illustrate whether cycloadditions (amoungst other pericyclic reactions) are thermally allowed. . It therefore possible to initially guess a transition state in computational analysis as to where a diene and dienophile are likely to lie directly before a Diels-Alder reaction takes place in a concerted manner. The interaction of the p orbitals of the dienophile and diene are hence required. Since these p orbitals lie in the same plane, the dienophile will need to approach the diene from the top or bottom face, but is normally the face which is less hindered (Fig.1 - note only the terminal p orbitals are shown in this diagram).

Fig. 2 The reaction profile for an exothermic reaction

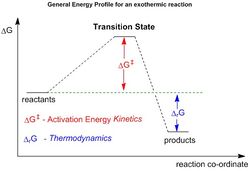
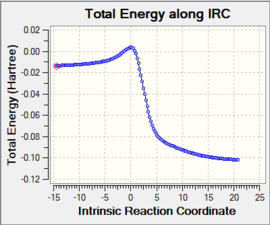
The transition states of the system may be carefully modelled by calculating the vibrations and geometry required by the diene and dienophile for a successful reaction to occur. Here, because the Diels-Alder reaction is concerted, there will only be one maximum in the reaction profile. In this case, the transition state may be defined as the point at which there is maximum energy (Fig. 2). It can hence be seen that the derivative of this point:

• $\frac{\partial \text{G}}{\partial \text{(r. co-ord.)}}=0$ and

• $\frac{{\partial }^2\text{G}}{\partial {\text{(r. co-ord.)}}^2}<0$

The Rate determining step, therefore, is the reactants having enough energy and the correct geometry to reach the transition state. It is also important to remember that the reaction co-ordinate is a 1-dimensional representation of a 3-dimensional system (i.e. a system which has three degrees of freedom).

In many cases, it is also possible to use Hammond's Postulate to predict what the transition state may look like; for example, an early transition state means that that the transition state resembles the reactants more than the product. The inverse may be said about a late transition state.

Nf710 (talk) 14:16, 24 February 2017 (UTC) Not quite, almost correct the reaction co-ordinate is in the normal mode basis which is 3N-6 and a TS is a maximum along one and a minimum along the rest.

Computational methods

All three experiments make use of the semi-empirical PM6 method to calculate reaction co-ordinates and energies for Diels-Alder reactions, at least initially in some cases. The method makes use of data collected from experiments to approximate certain variables. This method is ideal for large molecules which would take long to optimise immediately using DFT or Hartree-Fock. The problem with this method, however, is that since may approximations have been applied, the output may not reflect the system with complete accuracy. Density Functional Theory (DFT) B3LYP is a more advanced method and its basis is the electron density of the system. From this, the energy of the system may be estimated since the energy is a functional (function of a function) of the density. DFT makes use of prior computational methods developed such as Hartree-Fock to build on prior computational methods. For this reason, DFT may be considered a better method to use over PM6. However, comparing answers and outputs of the same chemical system from several different basis sets has no value, since each, although building upon the same principles, will use different Hamiltonian operators in calculations.

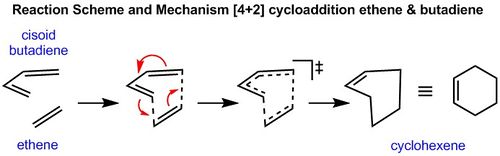
Exercise 1: Reaction of butadiene with ethene

Reaction Scheme

Scheme 1 Ethene and Butadiene

Molecular Orbital Theory and computational analysis

The MO diagram (Fig. 3) of ethene and cisoid butadiene can provide an insight into the fundamental expected orbital-bonding and orbital-antibonding interactions between the two structures in the transition state. Note that the two orbitals which state elsewhere are included to represent all 4 of the configurations of butadiene, but are not included in the frontier transition state orbitals.

Fig. 3 The Molecular Orbital diagram of the Frontier orbitals of ethylene and cisoid butadiene to form the [4+2] transition state.

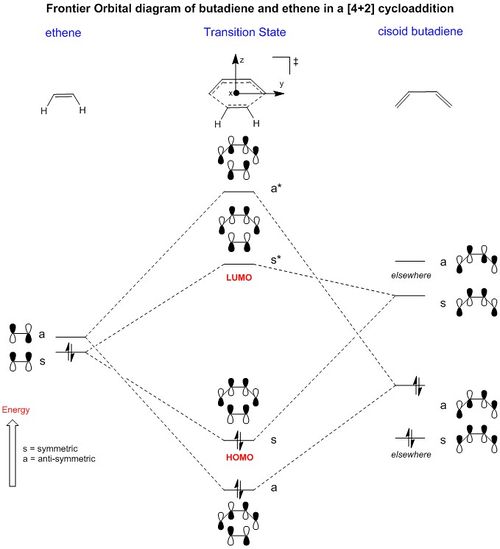
(Fv611 (talk) 12:05, 24 February 2017 (UTC) One of the nicest looking MO diagrams I've seen.)

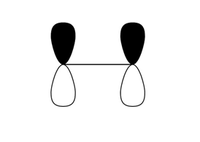
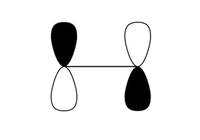
Only orbitals of ethene and butadiene of the same symmetry may interact. The MO diagram shows that there are only 2 possible symmetry allowed fragment orbitals or wave-functions which may form the transition state. The lowest in energy at the transition state is an a-a interaction of the LUMO of ethene and the HOMO of butadiene and the other is an s-s interaction with the HOMO of ethene and LUMO of butadiene. The reason for this is because it has been well established that for any quantum mechanical system involving symmetry:

• $A\times A=S$

• $S\times S=S$,

• $A\times S=A$ and similarly $S\times A=A$

This does not, however, give us an idea of the overlap integrals of each interaction. This can, instead, be explained by taking taking the linear combination of atomic orbitals to produce molecular orbitals, where:

• $⟨{\psi }_A|{\psi }_A⟩=\text{non zero}$

• $⟨{\psi }_S|{\psi }_S⟩=\text{non zero}$

• $⟨{\psi }_A|{\psi }_S⟩=0$ and $⟨{\psi }_S|{\psi }_A⟩=0$

Which shows that only orbitals of the same symmetry may interact with each other. Hence the HOMO of ethene and LUMO of butadiene; LUMO of ethene and HOMO of butadiene fulfil this criteria as the integrals are non zero and can therefore interact with each other, respectively.

(Fv611 (talk) 12:05, 24 February 2017 (UTC) Very good explanation of symmetry/overlap requirements.)

The orbitals produced by Gaussian correspond to the following:

Table 1 The HOMO and LUMO Gaussian generated orbitals of ethene and butadiene at PM6 level

Molecule	Gaussian Projection	MO HOMO	Gaussian HOMO	MO LUMO	Gaussian LUMO
Ethene
s-cis Butadiene

Table 2 Transition State orbital interactions between ethene and butadiene at PM6 level

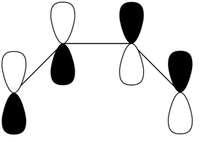
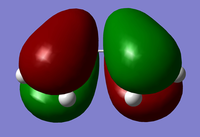
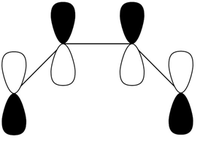
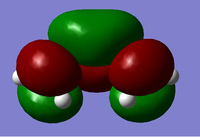Symmetry Label	Gaussian Projection	a	s (HOMO)	s* (LUMO)	a*
Front view
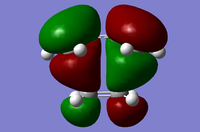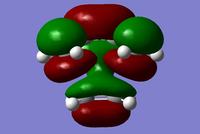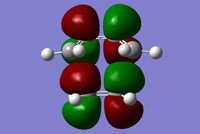Side View

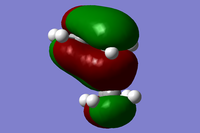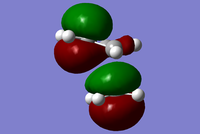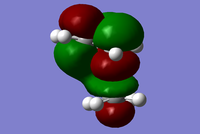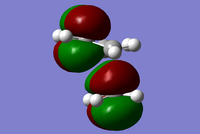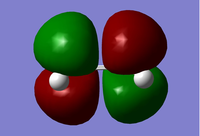
The MO diagrams show the molecular orbitals of the transition state. It is interesting to note that on the a (HOMO) and a* orbitals, there are no orbitals on the terminal carbon atoms. The reason for this may be because of the Semi-empirical/ PM6 method and basis set used. PM6 makes use of several approximations in order to simplify calculations and it may be possible that an over/under approximation may have occurred. There are also some secondary orbital interactions in the s* (LUMO) orbital between ethene and the forming double bond.

Below shows the Hartree-Fock calculated molecular orbitals of the system at the transition state:

MOs of HF calculated frontier orbitals at TS

The frontier orbitals above in the Jmol have been calculated with Hartree-Fock methods, which uses a different Hamiltonian and basis set. The job submitted to Gaussian was:

opt=(calcfc,ts,noeigen) freq hf/sto-3g integral=grid=ultrafine pop=full gfprint

The orbitals for s (HOMO) and a* now appear different and the p orbitals are more visible in this basis set. The orbitals are, however, at an angle and not directly above the terminal carbon atoms as predicted in the MO diagram. The reason for this is because as the transition state is approached, the carbons change from sp² to sp³. This change involves a change in hybridisation and geometry of the orbitals, and this is therefore shown in the generated orbitals.

It is, however, important to remember that these are only approximations. For the a, s* (LUMO) and a* show that the s orbitals on the hydrogen atoms on the ethene molecule are also involved in some way in the transition state. This is something not included in the MO diagram and is purely due to the basis set used and the way the Hamiltonian matrix has been resolved.

(Fv611 (talk) 12:05, 24 February 2017 (UTC) Good job on looking into the MOs more!)

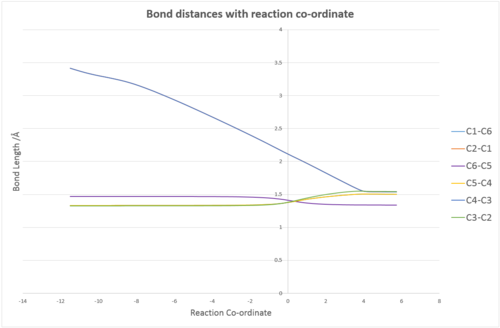
Bond Lengths

The bond lengths of the reaction may be monitored as the reaction progresses.

Fig. 4 How the bond lengths of the Diels-Alder change with reaction co-ordinate

Fig. 5 Refer to Fig. 4 when looking at specific carbon atoms

Animation 1 The reaction dynamics of ethene and butadiene to form cyclohexene

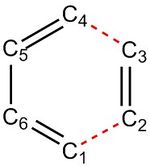
The graph shows four different lines for 6 different C-C bond lengths. The reason for this is because the cyclohexene transition state and product is symmetric and therefore there will be overlay between the C₁-C₆ and C₅-C₄ bond lengths. In addition, the two new sigma bonds at C₄-C₃ and C₂-C₁ will also overlap. This, hence, yields only 4 lines on the graph. From the graph, it is clear that the bond lengths of all the carbon-carbon double bonds at C₆-C₁, C₅-C₄ and C₃-C₂ start to increase in bond length (a pi bond turns into a sigma bond) whilst the C₂-C₁, C₄-C₃ and finally the C₆-C₅ bond lengths all decrease as 2 sigma bonds and 1 pi bond form. Table 3 below shows the bond lengths of the reactants, the transition state and the products. The scripts in brackets show the geometry and bonding in the reaction. For example, at the transition state, a pi bond which is breaking and turning into a sigma bond is denoted (π → σ) and is equivalent to stating that the geometry of the carbon atom is changing from (sp² → sp³) geometry.

Table 3 The changing bond lengths (to 2 d.p.) of the Diels-Alder reaction and bond type/Å.

	C1-C2	C2-C3	C3-C4	C4-C5	C5-C6	C6-C1
Reactants	-	1.33 (π)	-	1.34 (π)	1.47 (σ)	1.34 (π)
Transition State	2.11 (→ σ)	1.38 (π → σ)	2.11 (→ σ)	1.38 (π → σ)	1.41 (σ → π)	1.38 (π → σ)
Products	1.54 (σ)	1.54 (σ)	1.54 (σ)	1.50 (σ)	1.34 (π)	1.50 (σ)

The crystal Van der Waals radius of carbon is 1.70 Å . If 2 carbon atoms are considered to be just touching each other, then the total Van der Waals radius is equal to 3.4 Å (1.7 Å + 1.7 Å). Gaussian software does not take into account when displaying bond lengths the volume of the atom and considers the atom as a point. This means that all bond lengths displayed above in Table 3 are in fact distances from one carbon centre to another. For the sigma bond being formed in the transition state, the bond length was calculated as 2.11 Å. Since 2.11 < 3.4 Å, the bond length falls within the Van der Waals radii and therefore the reaction is likely to proceed down the transition state to produce cyclohexene, rather than reverting back to the reactants.

Vibrations at the Transition State

Animation 2 Vibrations of ethene and butadiene at the transition state

The Transition State vibration vields a negative number in Gaussian (Animation 2). The value of the frequency is 949i cm^-1. Since a Diels-Alder reaction is concerted, it is intuitive that the bond making and breaking must occur simultaneously. This is evident in the vibration below, where the terminal carbon atoms on butadiene move down and ethene move up synchronously. It is also interesting to see that all four of these carbon atoms exhibit more sp³ geometry as they approach each other - an additional indication that this is the correct transition state vibration.

Exercise 2: The reaction of cyclohexadiene and 1,3-dioxol

Reaction Scheme

Scheme 2 1,3-Cyclohexadiene and 1,3-dioxole to form the Exo and Endo products.

MO diagrams and computational analysis

Fig. 7 MO Diagram of cyclohexadiene and 1,3-dioxole

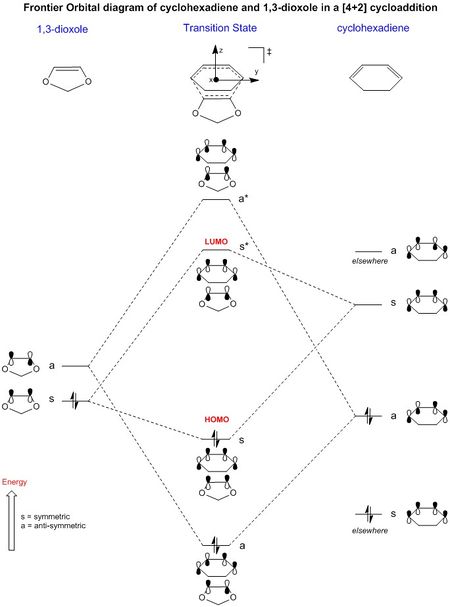
("elsewhere"... A broken line, zigzag or placing the energy levels in a box can be used to indicate their level is unknown or unimportant. Tam10 (talk) 11:09, 21 February 2017 (UTC))

The MO diagram for this reaction shows that this reaction is an inverse electron demand reaction. These reactions also fulfill the symmetry requirements for concerted reactions but the difference is that there is a greater interaction between the HOMO of the dienophile and the LUMO of the diene. This occurs when these two energy levels are close together in energy compared to the LUMO of the dienophile and HOMO of the diene. The inclusion of 2 oxygen atoms adjacent to the alkene in 1,3-dioxole leads to an increase in electron density at the alkene, thus increasing its energy and allowing for a better interaction with the LUMO of the diene.

Table 4 Molecular Orbitals of the transition state for both the Exo and Endo product

Endo Product	Exo Product

(Very nice use of script! Cutoffs have also been tweaked here to highlight the difference in secondary orbital overlap. However, don't use the word "product" Tam10 (talk) 11:09, 21 February 2017 (UTC))

The MOs of the transition state for both Exo and Endo Products are shown above optimised at the B3LYP/6-31(d) level. There are several secondary orbital interactions present in addition to those primary ones which may be predicted from the MO diagram above. In the Endo product, the main secondary orbital interactions are from the p orbitals on the oxygen atoms interacting with the s (LUMO) and a (HOMO) of the diene to produce these interactions in the s (HOMO) and a* (post LUMO) orbitals in the transition state. These p-p interactions do not form new bonds, but their presence does mean that the endo adduct from a [4+2] cycloaddition is the preferred product, hence giving rise to the endo rule. . Since these interactions are strongly present, it follows that the Endo adduct will form first because of a lower energy transition state.

The largest source of steric hindrance is from the two sp³ carbons on the 1,3-cyclohexadiene. These carbons may assist the approach trajectory in some respects since it forces the dienophile to attack from above/ below the plane of the molecule. However, these carbons may also clash with the additional sp³ on the 1,3-dioxole molecule.

Nf710 (talk) 14:29, 24 February 2017 (UTC) Which gives rise to what?

Reaction Energies

Table 5 Free energies of the Diels-Alder Reaction

Product	ΔG‡ / kJmol-1	ΔrG / kJmol-1	TS Frequency/ cm-1
Endo	+ 158.8	- 65.3	521i
Exo	+ 166.7	- 68.9	529i

The reaction energies in Table 5 show that the activation energy (E_a of this reaction at the B3LYP/ 6-31(d) level is calculated as +166.7 kJmol^-1 to form the Exo product and +158.8 kJmol^-1 to yield the Endo product. The difference in E_a between these two transition states is 7.9 kJmol^-1. The Exo product also has an energy of -68.9 kJmol^-1 relative to the reactants, and is lower in energy by 3.6 kJmol^-1 compared to the Endo product whose energy is -65.3 kJmol^-1 relative to the reactants. As a result of these activation ans reaction free energies, the Endo product is the kinetic product and the Exo is the thermodynamic product.

I think you have got your reaction energies mixed up here the endo should be both and your number are pretty much spot on but the wrong way round. Other than that excellent section.

Exercise 3: Diels-Alder v. Cheletropic

Reaction Scheme

Scheme 3 Diels-Alder and Cheletropic reactions

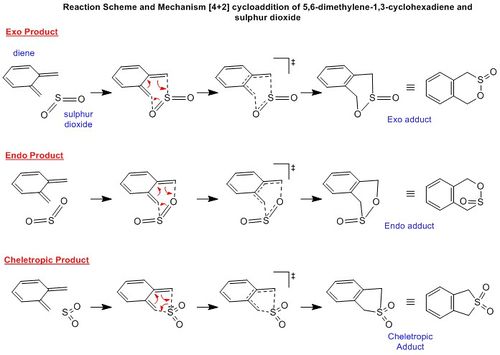
Reaction Energies

The reaction energies of the reaction are shown below, calculated at the Semi-empirical/PM6 level:

Table 6 The reaction of the diene and dienophile and their kinetic and thermodynamic free energies. Energies relative to reactants.

Product	Reaction Co-ordinate	ΔG‡ / kJmol-1	ΔrG / kJmol-1	Reaction Profile from IRC	TS Frequency / cm-1
Endo	alt text	+ 73.0	- 108.2	alt text	333i
Exo	alt text	+ 77.0	- 108.8	alt text	352i
Cheletropic	alt text	+ 95.4	- 165.3	alt text	486i

(Energies are consistently out by ~10 kJ/mol here, which would suggest an issue with the reactants Tam10 (talk) 11:09, 21 February 2017 (UTC))

Fig. 8 The reaction energy diagram of the Diels-Alder and Cheletropic reactions.

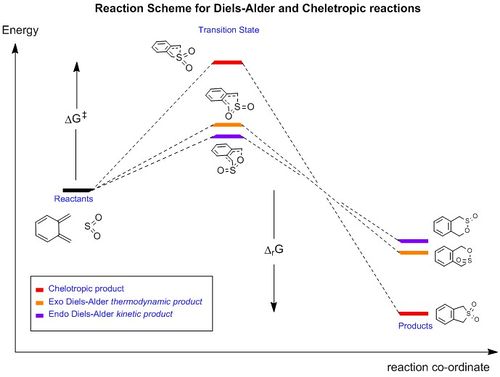
(Inclusion of the values of ΔG of activation and reaction can make the data easier to read Tam10 (talk) 11:09, 21 February 2017 (UTC))

The reaction scheme shows that the thermodynamically favoured product is that from the cheletropic reaction. This is because its products have the lowest energy and is 56.5 kJmol^-1 more stable that the Exo adduct. There is, however, very high activation energy which needs to be overcome and is 18.4 kJmol^-1 higher than the corresponding Exo transition state energy.

The Diels-Alder reactions show that the Endo product is the kinetic product and the Exo the thermodynamic product. A potential reason as to why the cheletropic product is significantly lower in energy compared to the Diels-Alder product is because (by referring to the animations in Table 6), there is some distortion in the 6-membered ring. This is likely to arise due to the 3 different atoms in the ring - carbon, sulphur and oxygen. Carbon and oxygen are in the same period however sulphur is one below. This means that the atomic radius of sulphur is much larger compared to the other atoms and is therefore likely to distort the ring. In the cheletropic product, because it is symmetric, the product does not have this distortion and would therefore be lower in energy compared to the Diels-Alder products.

Xylylene is unstable because the molecule is more stable once it has formed the aromatic benzene inside its structure. Both sp² carbons in the diene first vibrate together in a concerted motion to the oxygen and sulphur. These sp² carbons then turn into sp3 centres and the ring adjacent becomes aromatic. Again, the distorted structure is likely to be because of the reason outlined in the last paragraph.

Conclusion

Semi-empirical/ PM6 and DFT/ B3LYP,6-31(d) were used to investigate three Diels-Alder reactions and 1 cheletropic reaction. The outputs from the computations allowed for visualization of the transition state frequency and strongly supports that [4+2] cycloadditions are concerted subject to symmetry. The analysis of the free energies allowed for the construction of reaction energy profiles; and show that Endo products are kinetically favoured whereas Exo are thermodynamically. Further experimentation could be investigating the energy of a nickel metallacycle (a diene) as used in the trimerisation of alkynes to see how the free energy of the system differs when a metal with ligands is attached to the diene and undergoes a [4+2] cycloaddition with an alkyne.