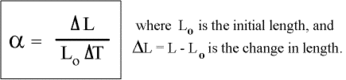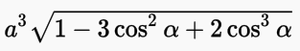Rep:Tmutimermgo

Investigation of the thermal expansion coefficient of magnesium oxide

Introduction

In this experiment the thermal expansion coefficient of magnesium oxide was investigated, by use of GULP and DLVisualise software.

Two different methodologies were used in order to determine a value for the coefficient, and the methods were compared in terms of their effectiveness.

The conventional unit cell of the face centred cubic lattice

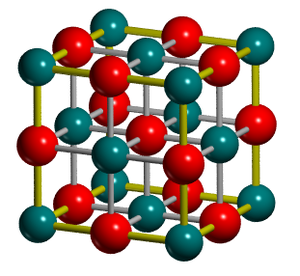
Magnesium oxide has formula MgO and in the solid state has a face centred cubic (fcc) geometry. The symmetry of the lattice means that there is only one lattice parameter, alongside a single angle; 60° for the primitive cell and 90° for the conventional cell. The structure of MgO is common of many other materials due to the high packing efficiency and high coordination number.

Quasi-Harmonic Approximation (QHA)

The first method used is a quasi-harmonic simulation, which optimises the lattice parameter such that the Gibbs free energy is minimised. At each temperature, the system is approximated such that it follows a harmonic potential, one consequence of which being that the equilibrium position of atoms is the same regardless of the vibrational energy level. If the system were simply modelled as one harmonic oscillator for the entire range of temperatures, the lattice parameter would be independent of the energy in the system and therefore independent of the temperature. This would mean that no thermal expansion could be calculated. However, in the Quasi-Harmonic methodology, the equilibrium distance effectively is manually varied.

In this method, the calculations consider k space (reciprocal space) as opposed to real space. A 3D matrix of points in k space is chosen. The matrix encompasses the boundaries of a single Brillouin zone, so the higher the number of points in the matrix, the more closely they are spaced. Because of the reciprocal relationship with real space, this is analogous to accounting for more and more neighbouring Wigner-Seitz cells, and so more and more vibrational modes are possible. The k_x, k_y, and k_z values that correspond to points of symmetry of the Brillouin zone, for example the centre, with coordinates (0,0,0) and label Γ, or the centre of a face or edge, are significant, as the energy levels possible at these points represent the possible vibrational modes a phonon may occupy. As the size of the matrix is increased, a greater number of combinations of k values lie on theses points, which is to say that more vibrational energy levels are possible.

The lattice parameter can be plotted against temperature in order to obtain a value of the thermal expansion coefficient. The type of unit cell that the parameter refers to, be it conventional or primitive, is irrelevant so long as it is consistent, as any ratio between parameters of different unit cells will remain constant if the thermal expansion is entirely symmetrical.

Molecular Dynamics

The second method used is molecular dynamics (MD) simulation. A supercell is constructed, which, in the case of this investigation, consisted of 64 atoms, equivalent to 32 primitive unit cells. The trajectory of each atom is calculated over a given time. The position of the atoms are calculated periodically simply by using equations of motion and integrating over a user-defined time period. In this way the simulation progresses such that the supercell approaches an equilibrium volume. This volume could then be used to determine the density of the bulk material, or, in the case of this experiment, is used to determine the thermal expansion coefficient.

Experimental Considerations

The range and number of temperatures simulated has to be sufficiently large in order to obtain an adequate linear fit, and so obtain an accurate value for the thermal expansion coefficient.

Quasi-Harmonic Approximation

An appropriately sized matrix must to be selected. Larger matrices are desirable as they entail a higher resolution of calculation and in turn, lead to a more accurate result; however, the offsetting consideration is that the larger the matrix, the larger the computational load. So an optimal matrix size will exist wherein the quality of the approximation is adequate but the time taken to calculate the results is still practical.

Molecular Dynamics

The time interval over which each calculation is done determines the effective 'framerate' of the output, but also importantly can affect the quality of the results if the interval is too long. When the sample rate is too low, it can misrepresent the motion of the atoms, as fast changes in velocity will be incorrectly accounted for, resulting in aliasing in the output data.

The number of equilibration frames must be sufficiently high, increasingly so at higher temperatures when a higher degree of expansion needs to be simulated; otherwise the system may not equilibrate within the timeframe.

Results and Discussion

Quasi-Harmonic Approximation

A phonon dispersion curve was calculated and is shown.

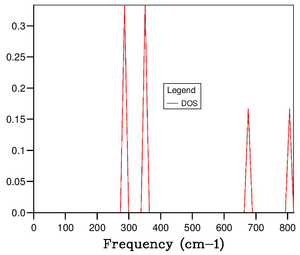
The density of states (DOS) was calculated using different matrix sizes. At the 1x1x1 size there were four peaks each corresponding to an energy level at the L symmetry point; coordinates (1,1,1). So for this particular matrix, the single point it contains corresponds to symmetry point L.

Left: DOS calculated from 1x1x1 matrix; Right: DOS calculated from 50x50x50 matrix

As the matrix size was increased the DOS became a broader and smoother distribution due to the increased number of energy levels available.

The following matrix sizes were selected for comparison, and shown alongside are the resulting calculated free energy values. Plotted is the range of values between matrix size 1x1x1 and 10x10x10.

plot of free energy against the size of matrix

Grid size	Free energy (eV)
1x1x1	-40.930301
2x2x2	-40.926609
3x3x3	-40.926432
4x4x4	-40.926450
5x5x5	-40.926463
6x6x6	-40.926471
7x7x7	-40.926475
8x8x8	-40.926478
9x9x9	-40.926479
10x10x10	-40.926480
20x20x20	-40.926483
50x50x50	-40.926483

At first, increasing the matrix size decreases the magnitude of free energy to a minimum at 3x3x3, then increases slightly to a plateau. At a size of 3x3x3 the value converges to within 0.5 meV of the plateau value and at 5x5x5 it converges to within an error of 0.1 meV. Considering these levels of precision, a 5x5x5 matrix was initially selected as optimal for the further calculations, given the reasonably short calculation times. Given that many other structures have the same fcc lattice, such as calcium oxide, the Brillouin zone is also of the same geometry (bcc), so a 5x5x5 matrix may also be effective with these analogous structures. Many other lattices including most metals, are bcc, meaning that the Brillouin zone is fcc and so has different symmetry points, and so the 5x5x5 matrix may not be appropriate for these cases.

The simulation was run at temperatures between 0 and 1000 K at 100 K intervals. The results are shown.

plot of the Gibbs free energy against temperature using the Quasi-Harmonic Approximation method.

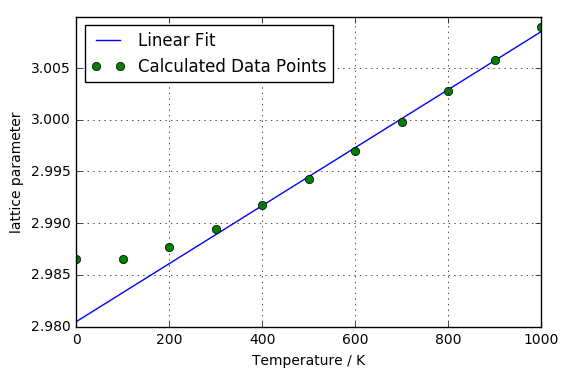
plot of the calculated lattice parameter against temperature using the Quasi-Harmonic Approximation method.

The linear fit shown included points from 300 K to 1000 K. A defined curve in the plot of the residuals for this fitted function shows that, despite the fact the data follows the linear fit reasonably well, in reality the expansion is still non-linear and so a polynomial fitted function would have theoretically been more appropriate.

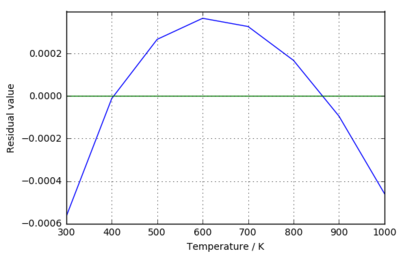
plot of the residual values between the collected data and the linear function that was fitted to it. Although the magnitudes are very small, a clear defined curve is an indication that a square or higher order polynomial fit would have been superior.

By utilising the following formula for the linear expansion coefficient:

Dividing the gradient of the linear plot by the magnitude of the lattice parameter at 300 K yielded a value for the linear expansion coefficient of 9.4e-6 K^-1.

The main approximation in this calculation is that the thermal expansion is linear with temperature, so a linear fit is used rather than using the more accurate, instantaneous gradient yielded by differentiating the curve, i.e. using δT and δL instead. As shown by the residuals plot, this is only ever an approximation as the true system doesn't have any perfectly linear regions. Another approximation is the fact that only limited numbers of k values are used, which doesn't truly represent the real system.

Molecular Dynamics

The molecular dynamics simulation, after some initial testing of the parameters, was run using 0.1 fs intervals and 1000 equilibration and production steps. The temperatures used were 100, 300, 600 and 1000 K.

Comparison of Quasi-Harmonic and MD Methods

The volume of the primitive cell was calculated using the data for the lattice parameter in conjunction with the following formula; volume equalling:

where a is the length lattice parameter and α is the angle lattice parameter.

For the representative temperatures of 100, 300, 600 and 1000 K, the volume of the primitive cell was plotted.

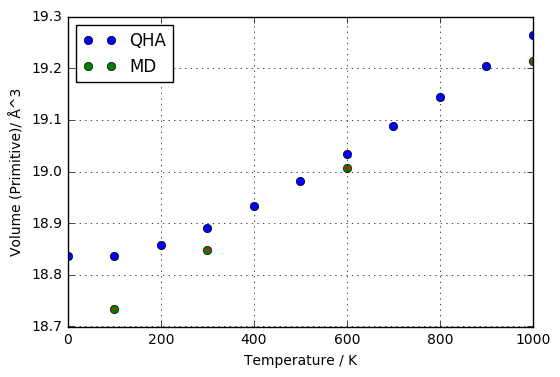
plot of the volume of the primitive cell of MgO against temperature using both QHA and MD respectively

Taking the cube root of the volume data for MD and doing a linear fit just as with the QHA, gave a value for the thermal expansion coefficient of 9.4e-6 K^-1.

The main approximation in this methodology is that a macroscopic crystal structure is being modelled as a crystal of 64 atoms. Each of the surface atoms doesn't have the same number of neighbouring atoms as the bulk, so experiences a different potential environment. This phenomenon is true but negligible in the macroscopic crystal but when using a supercell of relatively few atoms this may affect the quality of the simulation results.

The result yielded by the two methods was the same for the range 300-1000 K, to two significant figures, and both compare reasonably favourably with Haussuehl et al. value of 1.3e-5 K^-1. The two notable differences were that that the MD method gave slightly lower results at all temperatures, and that at temperatures below 300, the Quasi-Harmonic method produced a highly non-linear thermal expansion, and by inspection, a thermal expansion coefficient evaluated around 0 K would likely be very close to zero. The reason for the MD volumes being consistently lower may have been due to the fact that too small a time interval (0.1 fs) was used, or too few equilibration steps were used, which would result in the system not having enough simulated time to expand to equilibrium at each temperature.

Conclusion

Both of the methods for determining the linear expansion coefficient gave agreeing results. However they were much closer to each other than to any literature value. Perhaps the agreement of the two methods is partially coincidental, wherein the two methods were inaccurate to similar degrees, but caused by different sources of error and approximations. Another explanation is that literature values that are achieved empirically rather than computationally are higher due to the imperfect nature of the material that causes the thermal expansion to be greater than for an ideal crystal. This is perhaps due to defects weakening the overall bonding strength of the crystal, so the potential is more shallow, resulting in a greater displacement when the vibrational energy is increased by a given amount.