Rep:Title=Mod:yf1716
Optimizing Molecules Using Quantum Mechanics
This lab focuses on the use of quantum mechanical theory for the purpose of optimizing molecules that are being modeled. Optimization of a molecule means to represent it in a state where it has it's lowest energy. This was previously done using software that relied on force fields. Force fields have been programmed with manually inserted data, whereas Gaussian calculations are carried out with command input, indicating how the calculation should be run.
NH3
A molecule of ammonia |
Optimisation
The first molecule that was optimised is ammonia, NH3. The results of this optimisation are listed below.
| Data | Result |
|---|---|
| Calculation method | RB3LYP |
| Basis set | 6-31g(d.p) |
| Final Energy E(RB3LYP) | -56.5577687 a.u (7dp) |
| RMS gradient | 0.00000485 |
| Point group | C3v |
The table below indicates whether or not the forces have converged. One way that a system can achieve equilibrium is when all of the forces acting on it are balanced. Another way is if there are no forces acting upon it. In this case, we are searching for the latter. Since the values for force in the table are very close to zero, it can be said they have converged.
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Vibrational Analysis
Due to the 3N-6 rule, 6 vibrational modes were expected (3*4-6) and the computational analysis showed exactly that.
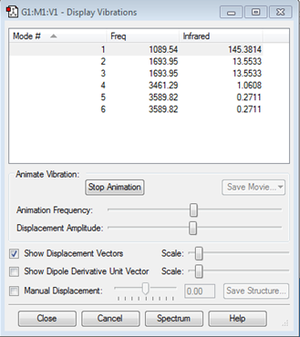
The data shows that modes 2 and 3 are degenerate with an energy of 13.5533 au. Modes 5 and 6 are also degenerate, with an energy of 0.2711 au. From the animation of the vibrations, it was seen that modes 1, 2 and 3 were bending modes whilst 4, 5 and 6 were stretching modes. The movement of atoms in mode 1 looked similar to an 'umbrella', with the central N atom and the attached H atoms moving in opposing vertical directions. Since two pairs of the modes are degenerate, it would be expected that there would be four bands in an experimental spectrum of gaseous ammonia.
Atomic Charges
Nitrogen is more electronegative than hydrogen, thus it would be expected that the central nitrogen atom would carry a negative charge, whilst the three hydrogens would be positive. The higher nuclear charge allows the nitrogen atom to polarise the covalent bonds, drawing higher electron density towards itself.
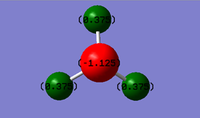
The charge on the nitrogen atom is -1.125 and the charge on all three of the hydrogen atoms is (+)0.375.
N2
A diatomic molecule of nitrogen (note, triple bond) |
Optimisation
The summary data from the optimisation of nitrogen is listed in the table below.
| Data | Result |
|---|---|
| Calculation method | RB3LYP |
| Basis set | 6-31g(d.p) |
| Final Energy E(RB3LYP) | -109.5241287 a.u (7dp) |
| RMS gradient | 0.00000060 |
| Point group | D∞h |
In a similar fashion to the previous optimisation of ammonia, the optimisation of nitrogen was confirmed by looking for force convergence. The table below shows that the optimisation was successful.
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Vibrational Analysis
The analysis showed that there was only one vibrational mode. This is in agreement with the 3N-5 rule for linear molecules (3*2-5). The animation showed that this was a bond stretch vibration. The frequency of this vibration was (+)2457.33 wavenumbers.
H2
A diatomic molecule of hydrogen (note, single bond) |
Optimisation
The summary data from the optimisation of hydrogen is listed in the table below.
| Data | Result |
|---|---|
| Calculation method | RB3LYP |
| Basis set | 6-31g(d.p) |
| Final Energy E(RB3LYP) | -1.1785394 a.u (7dp) |
| RMS Gradient | 0.00000017 |
| Point group | D∞h |
The table below shows that the force had converged, thus the optimisation was successful
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Vibrational Analysis
Similarly to nitrogen, hydrogen is a linear molecule. Therefore, application of the 3N-5 rule predicts that there should be one vibrational mode (3*2-5). This was indeed the case when vibrational analysis was conducted. This single mode was a bond stretch vibration with a frequency of (+)4465.68 wavenumbers.
The Haber-Bosch Process
This is the process by which ammonia is produced from it's constituent elements of nitrogen and hydrogen. The equation for the reaction is given as: N2 + 3H2 -> 2NH3 The energy for this reaction can be calculated by considering a series of steps.
• E(NH3)= -56.55776873 au • 2*E(NH3)= -113.1155375 au • E(N2)= -109.52412868 au • E(H2)= -1.17853936 au • 3*E(H2)= -3.53561809 au • ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 au
Since 1 atomic unit is equivalent to 2625 kJ/mol -0.0557907 au = -146.451 kJ/mol (3dp)
Small Molecule: F2
A diatomic molecule of flourine (note, single bond) |
Optimisation
Given below is the data from the optimisation of the flourine molecule
| Data | Result |
|---|---|
| Calculation method | RB3LYP |
| Basis set | 6-31g(d.p) |
| Final Energy E(RB3LYP) | -199.4982522 a.u (7dp) |
| RMS gradient | 0.00007365 |
| Point group | D∞h |
The table below confirms the convergence.
Item Value Threshold Converged? Maximum Force 0.000128 0.000450 YES RMS Force 0.000128 0.000300 YES Maximum Displacement 0.000156 0.001800 YES RMS Displacement 0.000221 0.001200 YES
Charge Distribution
Using Gaussian, the charges on each molecule were obtained. Given that it is a diatomic molecule and the atoms are identical, the charge on both atoms was zero. This is because the atoms have equal electronegativities, so attract electrons with equal force. Thus, no average polarisation is observed.
Vibrational Analysis
The vibrational analysis showed that there was only one vibrational mode, as predicted by the 3N-5 rule for linear molecules. This was a stretching mode with a frequency of 1065.09 wavenumbers.
Observing Molecular Orbitals

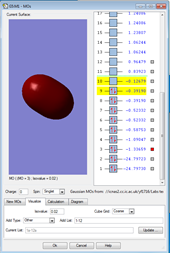
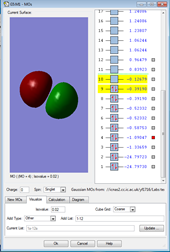
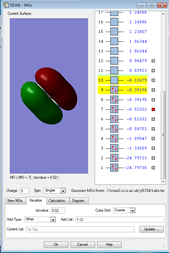

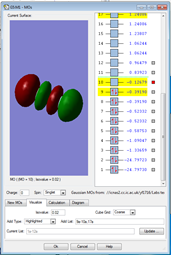

1.
This MO is made up of electrons from the 2s orbitals on each of the fluorine atoms. It is occupied. The MO is a bonding orbital and is deep in energy. Given that it is a bonding orbital, the electrons experience a greater positive charge, so the potential energy is reduced.
2.
This MO is made up of electrons from the 2s orbitals on each of the fluorine atoms. It is occupied and is an antibonding orbital deep in energy, but a higher energy than the bonding MO in image 1. Antibonding orbitals experience less positive charge since they are further away in space, so have a higher potential energy than boding orbitals.
3.
This MO is made up of electrons from the 2p orbitals on each of the fluorine atoms. It is occupied and is a bonding orbital deep in energy. The potential energy is thus lower than the corresponding antibonding orbitals.
4.
This MO is made up of electrons from the 2p orbitals on each of the fluorine atoms. It is occupied and is an antibonding orbital. Also, it is the highest occupied molecular orbital (HOMO) and hence It is the nucleophilic centre of the molecule.
5.
This MO is made up of electrons from the 2p orbitals on each of the fluorine atoms. It is unoccupied and is an antibonding orbital. Furthermore, it is the lowest unoccupied molecular orbital (LUMO) It is the electrophilic centre of the molecule.
