Rep:Title=Mod:sjh115TS
Introduction
In this experiment, Gaussian was used to locate and characterise the stationary points on the potential energy surfaces (PES) of three pericyclic reactions. They were characterised as minima or transition states by conducting frequency calculations in order to get an understanding the reaction profile of each reaction that was studied. These calculations also allowed the determination of the most thermodynamically and kinetically stable stereoisomer (i.e. exo vs endo in a Diels-Alder reaction) by examining the thermochemical information extracted from these calculations.
Potential Energy Surfaces
A Potential Energy Surface (PES) is a multi-dimensional surface plot which depicts the variation of potential energy across two or more reaction coordinates. The number of dimensions of this plot corresponds to the number of degrees of freedom the molecule possesses. This is 3N-6 for non-linear molecules and 3N-5 for linear molecules.
The reactants and products are minima of the PES, whilst the TS (transition state) is a maxima which is passed through to travel between the two. Both a minimum and a TS are stationary points and therefore will have first derivatives of 0 with respect to all degrees of freedom. A minimum point is one where a small fluctuation in any direction will give an increase in energy whereas the TS is a saddle point.
The landscape around a minimum has positive curvature in all directions, so the second derivative with respect to all degrees of freedom is positive at a minimum. As a transition state is a saddle point and therefore has negative curvature with respect to one degree of freedom but positive curvature with respect to all others. Therefore, a saddle point will have a single negative second derivative and positive second derivatives for all other degrees of freedom. This negative curvature for one point gives a negative force constant when calculating vibrational frequency modes of the molecules for the transition state. Using the equation below, the force constant (k) is square-rooted to get the wavenumber () and the square root of a negative number is imaginary, which is why every TS has a single imaginary vibrational frequency. This is a way to report whether the transition state that has been calculated has worked.[1]
[2]
Computational Methods
There were three methods used to get the initial structure of the transition state;
Method 1- A guess of the approximate geometry and optimise from there, this required prior knowledge of the TS.
Method 2- Method 1 was carried out with the interacting atoms were frozen before optimisation.
Method 3- The product was initially optimised and then broken apart into the constitutional components and optimised.
Two methods were used to calculate the optimised geometry of reactants, products and their transition states to varying degrees of freedom for the methods above. These calculations were carried out in a similar way by the computer in a step-wise fashion; first, a single point energy calculation was carried out to solve the Hamiltonian matrix for the molecule in that orientation. The geometry of the molecule was then varied and the single point energy calculation was run again. This cycle repeated until the structure of the molecule with the lowest energy geometries were located. The two methods varied in complexity.
Two computational methods were used when running calculations via GaussView are described below:
PM6- Is a semi-empirical method in which some of the Hamiltonian matrix is pre-set using empirically determined parameters. The accuracy of such calculations is limited due to these approximations.
B3LYP with a 6-31G(d) basis set- This is a DFT-hybrid technique through which the Hamiltonian matrix was solved as a function of electron density without pre-set parameters. This method also uses a Hartree-Fock calculation which accounts for the electron correlation exchange energy by calculating the Hamiltonian as a function of individual electron positions. Two methods (DFT and Hartree-Fock) are used as they complement eachothers shortfalls. This process is more computationally demanding but produces more accurate results.
Nf710 (talk) 17:41, 21 March 2018 (UTC) Nice Intro about the methods these are well explained. it would have been really nice if you could have out in some equations here to back up your discussion
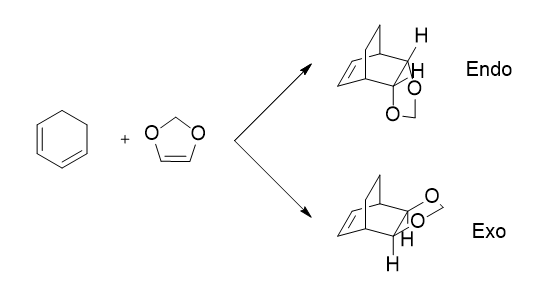
Exercise 1: Reaction of Butadiene with Ethylene
(Fv611 (talk) Good job overall, but you have the unoccupied TS MOs too high in energy in your diagram. As you haven't included the jmols of the reactants it's a bit hard to pinpoint exactly what went wrong.)
In this exercise the Diels-Alder cycloaddition reaction of butadiene and ethylene was explored. This reaction is thermally allowed under the Woodward-Hoffman rules as it involves 4s and 2s components.
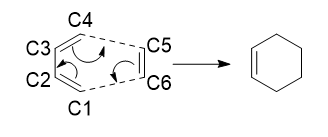
The reactants were first made and optimised to the PM6 level. Frequency analysis was used to confirm that they were optimised correctly; showing that there were no imaginary frequencies. The reactants were then used to locate the transition state via method one, which was then subsequently optimised to the PM6 level. This was confirmed to be the transition state after a frequency analysis yielded one imaginary frequency at -948.43 cm-1 and a further Intrinsic Reaction Coordinate (IRC) calculation also showed that it was the transition state. The IRC showed the reactants on the right to the products on the left and clearly showed that the gradient at each of the three points was zero. To further confirm that the transition state was correct an optimisation was ran on the product to make sure it was the minimum on the PES.

MO Diagram
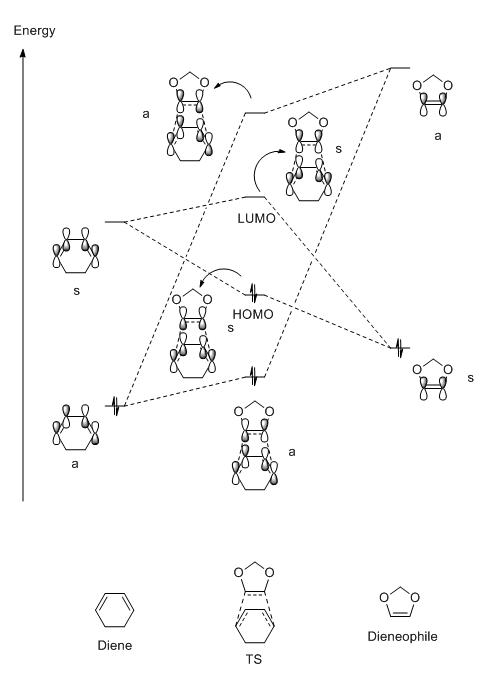
This MO diagram is used as a tool to help discover the origins of the transition state molecular orbitals (MOs) by analysing the interactions of the component MOs. The MO diagram is shown below and was produced by looking at the individual energies of each MO and placing them on the diagram relative to eachother MO energy.
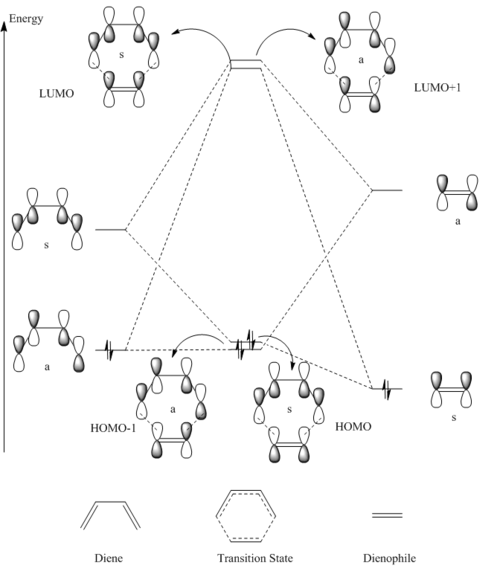
The reactant MOs combine to form the transition state MOs. This occurs via the interactions of the frontier orbitals of the reactants, ie their HOMOs and LUMOs. The HOMO of the butadiene interacts with LUMO of the ethylene to form two transition state MOs. The HOMO of the ethylene and the LUMO of the butadiene interact to form two more transition state MOs. The reactant MOs were further apart in energy than the first two, which means that the splitting was less so these two transition state MOs sit in between the first two that were produced. The MOs of the reactants only interacted with each other when the symmetry was the same between the orbitals, for the first interaction that was spoken about was the interaction of two asymmetric MOs. The second interaction was one between two symmetric MOs. The reason for this is that the the overlap integral between two orbitals that mix of the same symmetry is non-zero, whereas when the orbitals that mix are of different symmetry lead to an overlap integral of zero.
As the largest splitting comes from the asymmetric interaction of the reactant MOs the reaction can be seen to be normal electron demand. As this interaction involves the HOMO of the diene and the LUMO of the dienophile.
All the four transition state MOs formed on this diagram can be visualised below via the Jmols.
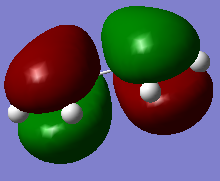 |
 |
 |
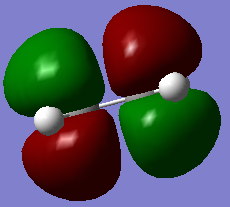 |
|
|
|
|
Bond Length Analysis
| Carbons bond (Å) | Reactants (Å) | Transition state (Å) | Products (Å) |
| C1-C2 | 1.33533 | 1.37976 | 1.50085 |
| C2-C3 | 1.46843 | 1.41104 | 1.33697 |
| C3-C4 | 1.33533 | 1.37980 | 1.50085 |
| C4-C5 | N/A | 2.11481 | 1.53714 |
| C5-C6 | 1.32742 | 1.38177 | 1.53458 |
| C6-C1 | N/A | 2.11481 | 1.53714 |
The typical bond length for a C(sp3)-C(sp3) single bond is 1.54 Angstroms and the typical C(sp2)-C(sp2) double bond length is 1.34 Angstroms.[3]
For the reactants there are three double bonds in total that match well with the 1.34 Angstroms from the literature values. The single bond on the butadiene is shorter than the literature single bond but this can be explained as it is an C(sp2)-C(sp2) single bond, so as theres more s-character the bond would be slightly shortened, as we see here.
As the reaction begins the three double bonds in the reactants elongate as they are becoming single bonds. The reverse process is happening for the C2-C3 in butadiene as the single bond becomes a double bond. As the length between C4-C5 and C6-C1 is 2.11481 Angstroms in the transition state, Which is less than double the Van der Waals radius of carbon (1.7 Angstroms), this suggests that bonds are forming between these carbons.[4] Two new bonds that are shown to formed between C4-C5 and C6-C1 as they have lengths very similar to a C(sp3)-C(sp3) single bond from the literature.
How Do These Bonds Form?
As the animation below depicts the two reactants are coming together without breaking the symmetry. As they move closer simultaneously the bonds that form between C4-C5 and C6-C1 form in a synchronous manner, which matches the theory of Diels-Alder reactions.

Log Files
Exercise 2:Reaction of Cyclohexadiene and 1,3-Dioxole
This exercise was completed differently to exercise 1 as the calculations for the optimisations and the transition states were calculated using the B3LYP level for a 6-31G(d) basis set after an initial minimisation at the PM6 level. The Diels-Alder cycloaddition of cyclohexadiene with 1,3-dioxole was investigated. This reaction also involved a π4s and a π2s component and thus is thermally allowed by the Woodward-Hoffman rules. However, with this reaction there are two trajectories of approach, ie ENDO and EXO, the reactions schemes are shown below. These varying orientations also result in different products so both trajectories were investigated.
MO Diagram
(Fv611 (talk) The MO diagram is good, but you should have discussed or showed the differences between endo and exo conformations in terms of relative energies)
As before the JMOl figures are below to depict the MOs for the transition states. The previous Diels-Alder reaction that was examined in exercise 1 was shown to be normal electron demand. However, this reaction was shown to be inverse electron demand as the diene LUMO-dienophile HOMO gap is smaller than the diene HOMO-dienophile LUMO gap, unlike before. The reason this occurs for this reaction is because of the oxygen atoms present in the 1,3-Dioxole. These atoms have electron donating effects, and hence can donate into the double bond. This raises the energy of both the HOMO and the LUMO for the dienophile component, resulting in inverse electron demand.
Nf710 (talk) 17:45, 21 March 2018 (UTC) Your conclusion is correct, however you have not proved this quantitively by looking at the single point energy.
|
|
|
|
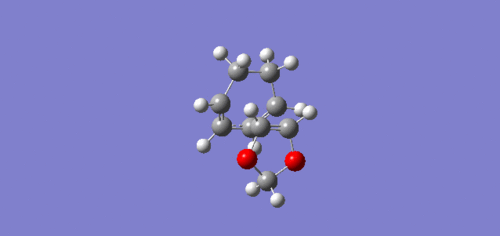
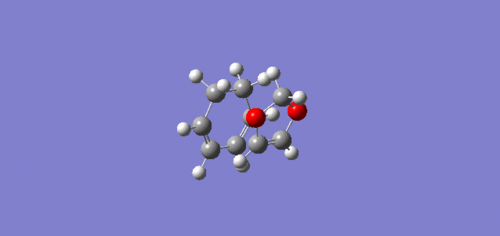
The Endo transition state was lower in energy and hence more stabilised than the Exo trajectory. This can be explained by the endo transition state having a secondary orbital, the lone pairs of electrons in the oxygen p-orbitals are able to interact with the orbitals situated at the back of the diene, which stabilises the transition state, which can be seen above in the endo HOMO JMol.[5]
 |
 |
Thermochemical Analysis
The table below shows the values of the reaction barrier and the reaction energies for both geometries in kJ mol-1. These values were calculated from free energies extracted from the results file under the heading 'Sum of electronic and thermal Free Energies' from the B3LYP optimisation with a 6-31G(d) basis set and converted from Hartrees to kJ mol-1.
| Reaction | Reaction Barrier (kJ mol-1) | Overall Reaction Energy (kJ mol-1) |
| Endo | 159.861 | -67.336 |
| Exo | 167.701 | -63.747 |
From the table above, it is clear to see that the endo reaction produces the kinetically favoured product. As this reaction pathway has the lowest energy transition state and thus it has the smallest reaction barrier. This therefore means that the endo product will be formed more rapidly and if the reaction was irreversible the reaction would be endo selective.
The endo trajectory has a smaller activation energy as a result of stabilising secondary orbital overlap. In the endo transition state, the lone pairs located in the oxygen p-orbitals are able to overlap and interact with the orbitals situated at the back of the diene, which can be seen clearly below. As the p-orbitals are positioned too far away from the back of the diene in the Exo transition state this stabilisation does not occur, hence why it is higher in energy.
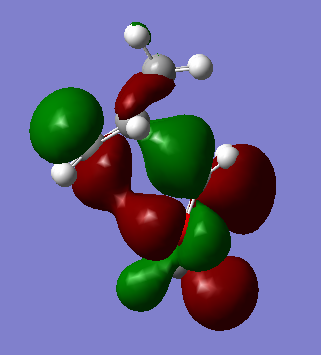
The theory of the thermodynamics of Diels-Alder reactions usually predicts the Exo trajectory to be the thermodynamically favorable pathway due to less sterics. However, in this particular example it is the Endo reaction pathway that has the lower reaction energy and so is the thermodynamically favored product. The reason for the exo adduct being higher in energy is because of an unfavorable steric clash between the hydrogens on the carbon between the oxygens on the 1,3-dioxole ring and the hydrogens on bridging carbons on the cyclohexadiene component.
Nf710 (talk) 17:49, 21 March 2018 (UTC) Good section your energies are correct and you have come to the correct conclusions. You could have gone into more detail in some places. Such as the theory behind the kinetics and the thermodynamics.
Log Files
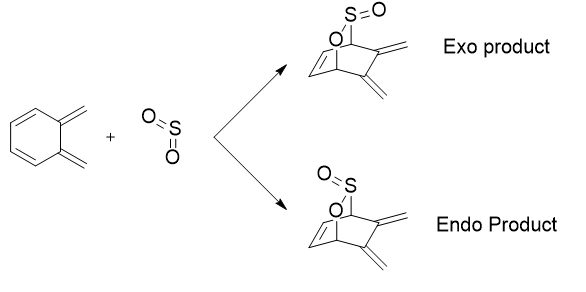
Exercise 3: Diels-Alder vs Cheletropic
The reaction between Xylylene and SO2 was investigated in this exercise. These reactants could react in one of three ways as shown above in the reaction scheme.
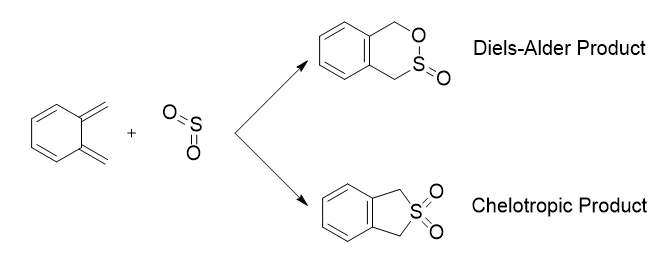
As with exercise one and two, both the endo and exo Diels Alder cycloadditions involve π4s and π2s components and thus are thermally allowed by the Woodward-Hoffman rules.
The cheletropic reaction passes through a cyclic transition state; thus is also classified as a pericyclic reaction. However the two new σ bonds formed terminate at the same single atom to form a five membered ring. This is how this reaction differs from the Diels-Alder cycloadditions.
The transition states for the three different reactions were located using method three and were optimised to a PM6 level. The reactions were confirmed to be at their respective transition state by having only one imaginary frequency as before. The transition states were further confirmed by running IRC calculations.
Reaction at the Exocyclic site
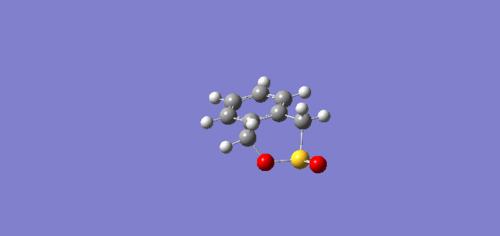 |
 |
 |
From the IRC calculations it can be seen that both types of Diels-Alder reactions (endo and exo) proceed in an asynchronous manner as the resultant bonds are not formed simultaneously. Whereas the chelotropic reaction is shown to be synchronous by the animations of the IRC above. (You may have to click on the animations for them to move as the page takes a while to load.)
Thermochemical Analysis
Using the same method as for exercise 2, the reaction barriers and energies were found for the three pathways in this exercise.
| Reaction | Reaction Barrier (kJ mol-1) | Overall Reaction Energy (kJ mol-1) |
| Exo | 84.665 | -100.761 |
| Endo | 80.755 | -100.121 |
| Chelo | 102.988 | -157.097 |
From the table above, it can be seen that the endo reaction pathway has the smallest reaction barrier so this reaction has the lowest energy transition state. This therefore means that the endo product is the kinetically favoured product and thus will be formed faster in reactions. The endo trajectory benefits in the form of stabilisation from secondary orbital overlap of the π systems in the transition state which lowers the activation energy of this pathway.
However the relative difference between the values of the reaction barrier for the endo and exo is small. This is because the secondary overlap has a smaller effect in the case of this reaction as a consequence of sulphur dioxide being a much smaller dienophile than the dioxole that we saw in the previous exercise. As these values are so close with the PM6 level of calculation used, the actual values could be slightly different, so a further calculation with the B3LYP level for a 6-31G(d) basis set would be useful to differentiate these reaction pathways more thoroughly.
The cheletropic reaction has the lowest energy adduct and so can be deemed as the most thermodynamically favoured product. As the resulting product has enthalpic stabilisation due to the extra S=O bond in its structure compared to the Diels-Alder products. However the reaction barrier is highest of the three reactions. This can be credited to the formation of the five membered ring as this is more unfavourable because of increased strain caused by smaller bond angles than the six membered ring formed in the Diels-Alder reactions. All the reactions experience the stabilisation of the Xylylene reactant by making it aromatic, making all the reactions have such low energy products.
Below is the reaction profile for this exercise, which summaries all the thermochemical values discussed above.
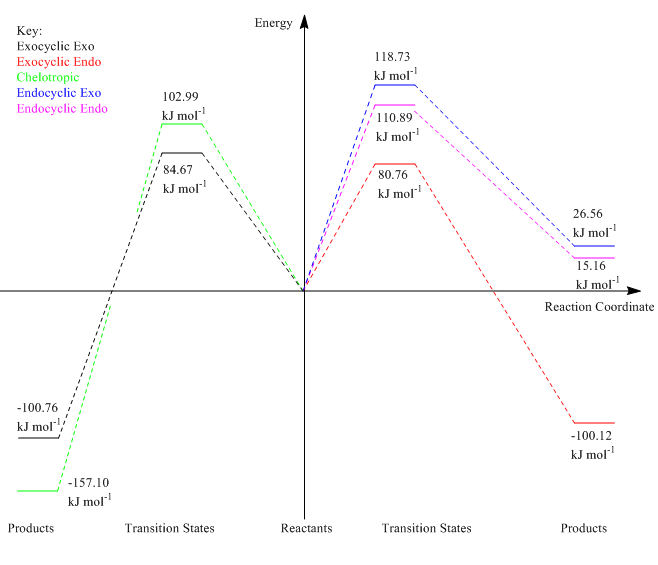
(A slightly random choice for what goes left and what goes right, but the data is clear Tam10 (talk) 12:21, 5 March 2018 (UTC))
Xylylene is very unstable, it readily undergoes rearrangements in order to become more stable. This does not occur in this reaction because the xylene ring becomes aromatic in the product which makes it much more stable. It can be seen that the bonds in the xylene ring all become the same length in the product as it becomes aromatic.
Reaction at the Endocyclic site
Xylylene has a second cis-butadiene fragment in the ring which is also able to undergo Diels-Alder reactions with sulfur dioxide. These reactions are depicted in the scheme below and can be visualised using the IRC animations below. The reactions can occur with two trajectories like before; exo and endo. Both of these reaction trajectories are asynchronous.
 |
 |
Thermochemical Analysis
Using the same method as for exercise 2, the reaction barriers and energies were found for the two alternative trajectories.
| Reaction | Reaction Barrier (kJ mol-1) | Overall Reaction Energy (kJ mol-1) |
| Exo | 118.73 | 26.56 |
| Endo | 110.89 | 15.16 |
Both reactions are endothermic, ie theres a positive reaction energy, so they require an input of energy to proceed. When comparing the endocyclic reaction pathway to the exocyclic reaction pathway it can be see that the endocyclic trajectories are both highly kinetically and thermodynamically unfavourable. The main reason for this is that the formation of the six-membered aromatic ring does not occur in the endocyclic reactions, which was one of the major driving forces in the other reactions. They are also kinetically unfavourable due to the ring strain.
Log Files
Exocyclic Exo Transition State
Exocyclic Endo Transition State
Endocyclic Exo Transition State
Endocyclic Endo Transition State
Extension: Ring Opening of the Cyclopropyl cation
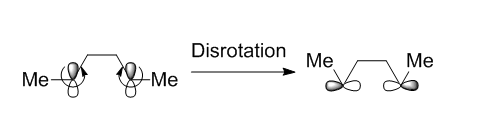
The ring opening of the cyclopropyl cation was completed using method 3 from the introduction and the reaction scheme is shown below. Once the transition state was obtained, the IRC clearly showed disrotation of the methyl groups present.
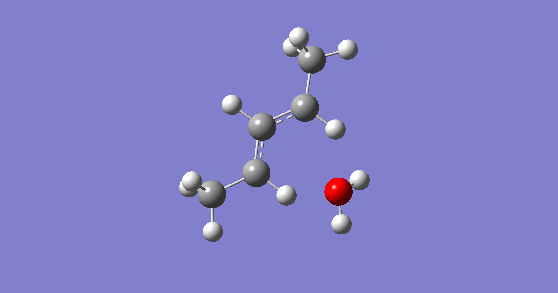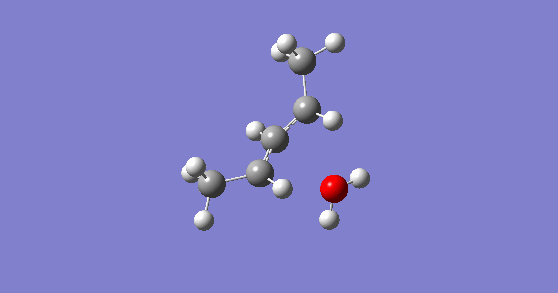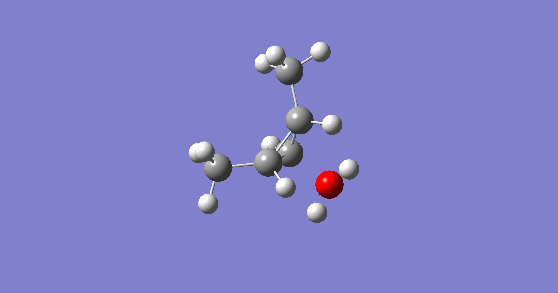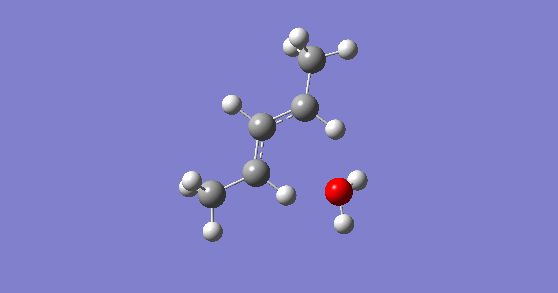
The animation of the IRC above shows the transition from products (ring opened) to reactants (ring closed). Opening of a cyclopropyl cation to an allylic cation is a 2-electron system which is the smallest system capable of undergoing an electrocyclic reaction, the reaction is disrotatory. The removal of the tosylate and the ring opening occur simultaneously, which can be seen in the animation of the IRC below, so this reaction is a solvolytically-assisted pericyclic reaction.
The explanation of why the reaction is distrotatory is as follows; When like phases of the p orbitals are on the same face of the molecule, the two orbitals must rotate in opposite directions, one clockwise and one anticlockwise, in order for the orbitals to overlap to form a σ-bond. The rotations in opposite directions of the orbitals gives this disrotatory effect.[6]
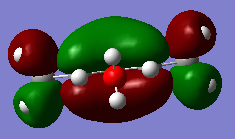 |
 |
Thermochemical Analysis
| Reaction Barrier (kJ mol-1) | Overall Reaction Energy (kJ mol-1) |
| 56.4587 | -104.448 |
The reaction is exothermic as the overall reaction energy is negative. This can be justified as the release of ring strain is favorable to give a less constraint structure. The same reason can lead to the low reaction barrier as the molecule is looking to have a less restricting structure.
Log Files
Conclusion
The practical was successfully performed on all exercise using the PM6 and B3LYP computational methods in the graphical user interface of Gaussian; GaussView. It was shown that these methods could be used to locate the transitions states of even relatively complex reactions, in a reasonable amount of time, aided by chemical intuition. The PM6 level performed quicker but optimised structures to a lower accuracy due to the high degree of approximations used in this theory.
In conclusion, these experiments have shown that the that stabilising secondary orbital overlap between p-orbitals on the dienophile and the orbitals at the back of the diene in the the endo transition state leads to the reaction barrier usually being lower than the exo configuration. However, the exo adduct is usually the more thermodynamically favourable of the two due to less steric hindrance as the molecule is less compact. Exercise two proved that the difference in reaction energies for the two orientations is small enough that sterics can cause an increase in the energy of the exo product making it no longer the thermodynamically favourable adduct.
References
[1] Lewars, E. G. (2011). Computational Chemistry. http://doi.org/10.1007/978-90-481-3862-3
[2] Atkins, P. W., & DePaula, J. (2014). Physcial Chemsitry (Vol. 10th). OUP Oxford.
[3] Craig, N. C., Groner, P., & McKean, D. C. (2006). Equilibrium structures for butadiene and ethylene: Compelling evidence for II-electron delocalization in butadiene. Journal of Physical Chemistry A, 110(23), 7461–7469. http://doi.org/10.1021/jp060695b
[4] Batsanov, S. S. (2001). Van der Waals Radii of Elements. Inorganic Materials Translated from Neorganicheskie Materialy Original Russian Text, 37(9), 871–885. http://doi.org/10.1023/A:1011625728803
[5] Jursic, B. S., & Jursic, B. S. (1997). A Density Functional Theory Study of Secondary Orbital Overlap in Endo Cycloaddition Reactions. An Example of a Diels-Alder Reaction between Butadiene and Cyclopropene. The Journal of Organic Chemistry, 62(10), 3046–3048. http://doi.org/Doi 10.1021/Jo9620223
[6] Claydon, J., Greeves, N., & Warren, S. (2001). Organic Chemistry. OUP Oxford.
