Rep:Title=Mod:SSH214ts

Introduction

[4+2] cycloaddition reactions between diene and dienophile occur via a concerted mechanism. The transition state is cyclic in nature. 2pi bonds are broken to form to new sigma bonds and one new pi bond. Woodward Hoffman rule is applied to check whether the reactions are thermally allowed. Reactions between the HOMO of the diene and the LUMO of the dienophile is known as normal electron demand, whereas when the LUMO of the diene reacts with the HOMO of the dienophile, it is known as inverse electron demand. This experiment shows the effect on orbitals and transition state state energy as electron withdrawing and donationg groups are altered in the reactants, hence effecting the orbital overlaps in the reactions. The activation energy of the reaction is the energy required to overcome the barrier to form products from reactants. It depends on a number of factors and can be estimated using the gaussview program. Once the transition state is optimised, the Intrinsic reaction Coordinate can be used to determine the activation energy of the reaction. As the reaction is concerted in nature, no intermediates are involved that makes the computational analysis much more simpler.

Transition state is known to be the maximum peak in a reaction coordinate graph. For this point, the second derivative is a negative value and the first derivative of the graph equation is 0. On the other hand, potential energy is the function of energy vs reaction coordinates. It has dimensions of 3N-6. All dimensions are found to be positive in Gaussian except the transition state. Hence there is a negative frequency in the results, which is an imaginary frequency due to the negative value of the secondary derivative.

Nf710 (talk) 21:07, 16 April 2017 (BST) There is only one reaction coordinate that is the dimension of the TS which has the negative curavture. THe PES is in the basis of the normal modes which are linearly independant to eact other wrt to energy.

Two methods used are SEMI EMPIRICAL PM6 and DFT/B3LYP. "Both method describes the quantum states of many electrron systems and solves the electronic degrees of freedom, using the born oppenheimer approximation, The Hartree-Fock method assumes that the many-electron wavefunction takes the form of a determinant of single-electron wavefunctions, called a Slater determinant. The problem associated with this, is that a general many-electron wavefunction cannot be stated as a single determinant. Hence, electronic correlation is not incorporated by Hartree-Fock methods and the follow-on energies tend to be too high. If the complete basis of single-electron wavefunctions is found, then the express exact many-electron wavefunction can be expressed as a linear combination of all possible determinants made of these wavefunctions. This is called Configuration interaction.

In density functional theory (DFT), the many-electron wavefunction is completely bypassed in favor of the electron density. Due to to the the Hohenberg-Kohn Theorems, the ground state energy of the system depends uniquely on the electron density, for example the total energy is a functional of the electron density. Therefore, the variational principle can be applied to reduce the energy with respect to the electron density. The problem with this technique is that the energy functional is not known. At the first level of approximation, the local density approximation (LDA) could be used, where it is assumed that the energy depends locally on the density in the same way it does for a uniform electron gas. Modern methods use generalized gradient approximations (GGAs) where the gradient of the density is taken into account to produce a more accurate functional. However, the exact energy function is still unknown and is a big open problem in computational chemistry and condensed matter physics.

Hartree-Fock and its descendants were considered more reliable than DFT, but this has changed recently as DFT techniques have become more refined. Moreover, whereas in Hartree-Fock type calculations, track must be kept of the spatial and spin coordinates of all NN electrons, DFT offers the potential benefit of dealing with only a single function of a single spatial coordinate. For this reason, DFT has been steadily gaining in popularity in recent years."

The method that was used in this experiment involved, starting from products, optimizing the structure, breaking the bonds that were formed in the transition states, freezing the atoms involved in bond forming, optimising the structure again and then carrying out the transition state analysis at semi-empirical PM6 for exercise 1 and 3 and DFT/B3LYP for exercise 2. Exercise 1 is the reaction between butadiene and ethene. Exercise 2 is the reaction between benzoquinine with cyclopentadiene and exercise 3 is the reaction between xylene with sulfur dioxide.

Nf710 (talk) 21:14, 16 April 2017 (BST) Its weird that you quoted that. Its a pretty good summary. If you understand it.

Exercise 1:

The [4+2] cycloaddition reaction between butene and diene is fairly simple for computational analysis. The reactants do not contain any electron withdrawing or electron donating groups, to lower the LUMO of the dienophile or raise the HOMO of the diene. Hence there is a large energy gap and poor orbital overlap between ethene and butadiene and hence poor reactivity. But the approach from any side will produce the same product.

Figure 1: (reaction scheme of exercise 1).

C-C bondlengths

Figure 2: (carbon numbering).

C-C	Bond lengths in reactant (Å)	Type of bond	Bond lengths in TS (Å)	Bond length during reaction	Bond lengths in product (Å)	Type of bond
1,2	1.33345	sp2	1.37975	lengthening	1.50031	sp3
2,3	1.47082	sp3	1.41114	shortening	1.33702	sp2
3,4	1.33344	sp2	1.37975	lengthening	1.50031	sp3
4,5	na	2 x VdW	2.11492	shortening	1.54008	sp3
5,6	1.32755	sp2	1.38178	lengthening	1.54089	sp3
6,1	na	2 x VdW	2.11435	shortening	1.54008	sp3

The table above summarizes the C-C distances as reactants form product. The C-C double bonds are shorter in length than C-C single bonds. Hence C2-C3 decreases in length as it changes from single to double bond. At the same time, the C1-C2 and C3-C4 length increases as it changes from double bond to single bond. The literature value for the vander waals radii of C is 1.70 A and 2 X VDW of C is 3.40 A. C1-C6 and C4-C5 are shorter than this value in the TS which indicates than there is bond formation. sp3 C-C = 1.57 A and sp2 C-C = 1.33 A.

The formation of the two bonds are synchronous as the C1-C6 and C4-C5 have the same length in the TS. Both are forming sp3 bonds. Both sigma bonds are forming at the sane time in this concerted mechanism.

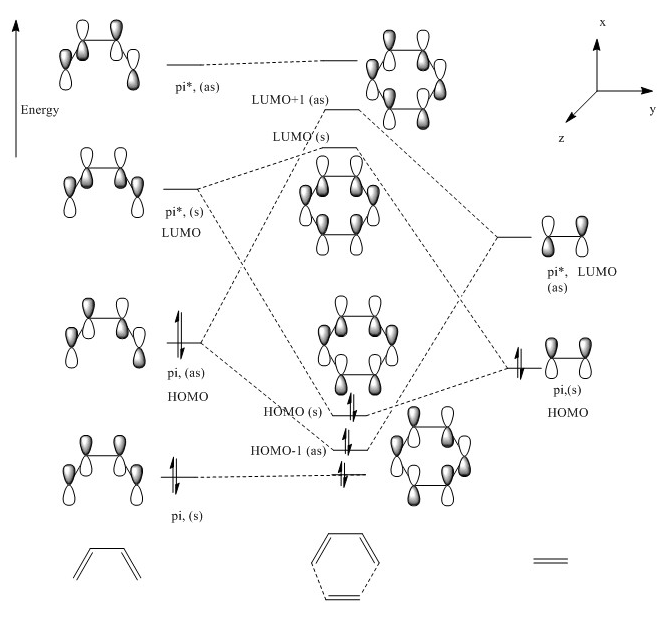
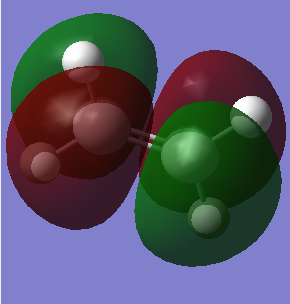
MO of ethene and butadiene and transition states:

Butadiene
HOMO	LUMO
Ethene
HOMO	LUMO

The MOs of the orbitals have assigned symmetry labels 's' for symmetric and 'as' for antisymmetric. Only 's-s' or 'as-as' interactions are allowed and has a non-zero orbital overlap integral. Hence the orbitals that can interact are the HOMO of the butadiene and the LUMO of the ethane being both antisymmetric and the LUMO of the butadiene and the HOMO of the ethene being both symmetric. The other MOs don’t interact because of difference in symmetry labels or too differences in energy gap. For symmetric-antisymmetric interaction, orbital overlap integral is 0, for symmetric-symmetric interaction the integral is nonzero and for an antisymmetric-antisymmetric interaction it is also nonzero, according to the LCAO principle.

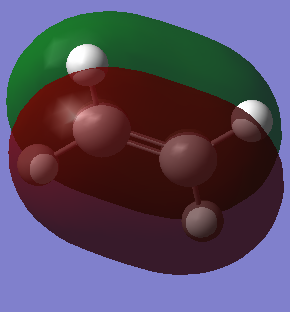
MOs of the TS of the cycloaddition between ethene and butadiene
MOs for the Diels Alder reaction

| |}

negative frequency=-948.81 cm-1

first positive frequency=145.12 cm-1

IRC of exercise 1.

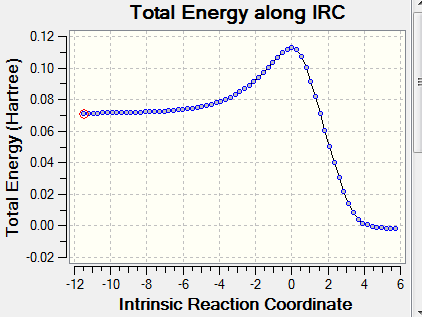
The animation shows the transition state scenario. A single negative frequency in results confirms the transition statte, which is further confirmed by the IRC. The IRC also confirmed that there were no intermediates or any other transition state involved. The activation energy is the height difference between the reactant and the TS. This determines whether the reaction is allowed or forbidden. Woodword Hoffman rules are used to determine the possibility of the reaction.

Exercise 2:

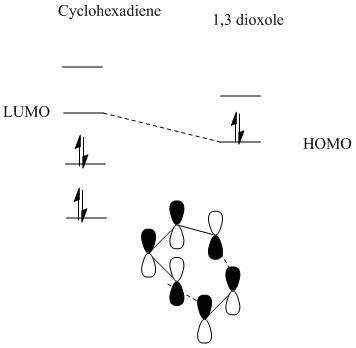
This exercise is less simpler than the previous exercise as the cycloaddition between benzoquinone and dioxole can form two possible products and hence two possible transition states are available now.The two possibilities are exo and endo. There is a difference in activation energy in both the exo and the endo states, as the approach trajectory is different and this leads to differences in orbital interactions.

MOs of reactants and transition states

diene
HOMO	LUMO
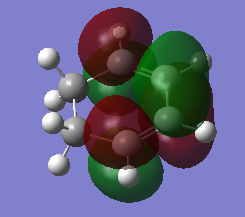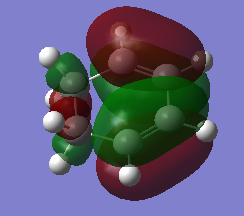
dienophile
HOMO	LUMO

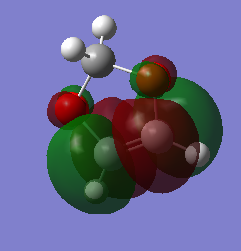(This is an MO correlation diagram, not an MO diagram. You have information about where the TS MOs lie, so you should use that to create a full MO diagram. Also, you haven't labelled the symmetries of any of the orbitals or what they look like. It should be similar to what you have in exercise 1. Tam10 (talk) 11:17, 5 April 2017 (BST))

Frontier MOs for the endo TS

Frontier MOs for the exo TS

In this exercise, the dienophile has electron donating groups that raises the energy of both the HOMO and the LUMOs. On the other hand, the energy of the cyclohexadiene MOs stays fairly the same as there is no electron donating or accepting groups present. The energy gap between the HOMO of the dionophile and the LUMO of the diene is small enough to interact, resulting in an inverse electron demand Diels alder reaction.

Energy

TS	Energy of reactants (kJ/mol)	Energy of TS (kJ/mol)	Energy of the product (kJ/mol)
Endo	0	+158.42	-66.51
Exo	0	+166.89	-62.71

"At room temperature, kinetic reaction control prevailed and the less stable endo isomer was the main reaction product. At higher temperatures and after long reaction times, the chemical equilibrium can assert itself and the thermodynamically more stable exo isomer can be formed. The exo product is more stable by virtue of a lower degree of steric congestion, while the endo product is favoured by orbital overlap in the transition state."

The activation energy was calculated using energy results of reactants and transition states. The Ea of the endo product was found to be 8.47 kJ/mol lower than the exo product due to better orbital interactions in the TS.There is secondary orbital interaction in the endo prodcut that lowers the activation energy of the transition state and hence the endo product is more kinetically favored. The reaction energy of the endo product was more negative compared to the exo product, hence it was the thermodynamically favourable as well.

It can be seen that the HOMOs of the exo TS has mainly primary orbital overlap interactions. On the other hand, the HOMOs of the endo TS has secondary orbital interactions between the diene and the dienophile, that helps to lower the barrier energy.

Nf710 (talk) 21:29, 16 April 2017 (BST) Your energies are correct an you come to the correct conclusions, you could have backed up the arguments with some diagrams.

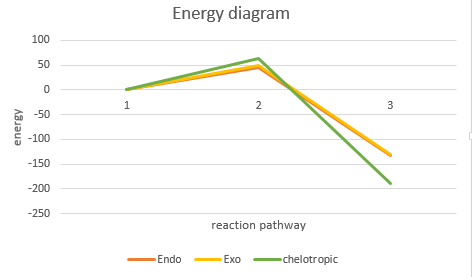
Exercise 3:

In this exercise we examined the reaction between o-xylylene and sulphur dioxide. Three possible products, exo, endo and chelotropic reactions were determined. Presence of one negative frequency confirmed the accuracy of this state. The reaction pathways were concerted but not fully synchronous. The C bonding to the O was seen to be faster than bonding to S since being in period 2, C and O have similar sized orbitals and hence have better overlap. On the other hand, S which is in period 3, is much larger in size and have poorer orbital overlap.

(Don't put too much trust in GaussView's determination of a 'bond'. It uses distance cutoffs to decide whether to put a line between atoms. Tam10 (talk) 11:17, 5 April 2017 (BST))

TS	Energy of reactants (kJ/mol)	Energy of TS (kJ/mol)	Energy of the product (kJ/mol)
Endo	0	+45.61	-132.66
Exo	0	+49.53	-129.86
chelotropic	0	+64.43	-188.67

(These energies don't match any that we have. Unfortunately you haven't given the energies of your stationary points or their log files, so I can't see how you landed on those values Tam10 (talk) 11:17, 5 April 2017 (BST))

Energy path

It can be seen that the endo pathway is favoured as the activation energy involved is the least compared to the exo and chelotropic reactiions. This is for the same reason as better secondary orbital overlap interactions. The chelotropic product is likely to occur at higher temperatures since it has a higher activation energy.

The table below shows the animations of the three reactions and the IRC paths assocated with it.

Chelotropic IRC path
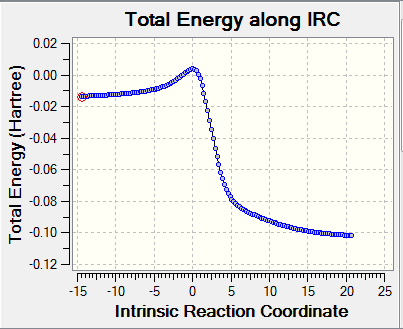
Exo IRC path
Endo IRC path

: (Dimerisation of xylylene).

Xylylene can easily dimerise to form benzocyclobutene as seen in the figure to the left.

Xylylene is highly unstable.The energy of the product drops increasingly as it bonds top the 6 membered ring. This is due to the resonance gained by the delocalisation of the pi system.

Conclusion:

For all the three reactions, the transition states were figured out. The HOMO and the LUMO orbitals were investigated.The IRC confirmed no intermediates present in the reactions. In Exercise 1, the C-C was shorter than the Vander walls radii in the TS, which confirmed the forming of bond. In Exercise 2, the endo product was kinetically and thermodynamically favored over the exo product. In exercise 3, the xylylene can react with SO2 to form 5 different products, three of which were investigated. The chelotropic product was the least likely product to form among the three.

References:

<references> <references>