Rep:Title=Mod:NAS13

EX₃

Optimisation and Frequency

bond lengths and angles

Property	BH3	BBr3	GaBr3
r(E-X)/angstrom	1.19	1.93	2.90
θ(X-E-X)/deg	120.0	120.0	120.0

BH₃

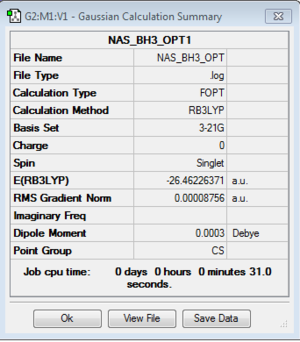
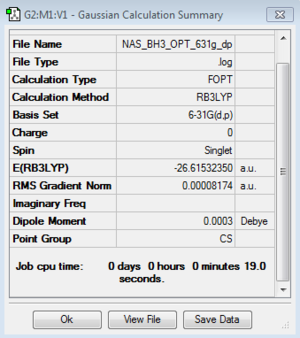
B3LYP/3-21G level

Optimisation log file here

Table showing settings, proof of convergence and optimised molecule

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000217 0.000450 YES RMS Force 0.000105 0.000300 YES Maximum Displacement 0.000900 0.001800 YES RMS Displacement 0.000441 0.001200 YES	optimised BH molecule

B3LYP/6-21G (dp) level

Optimisation log file here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000203 0.000450 YES RMS Force 0.000098 0.000300 YES Maximum Displacement 0.000867 0.001800 YES RMS Displacement 0.000415 0.001200 YES	optimised BH molecule

Frequency log file here

summary data	low modes
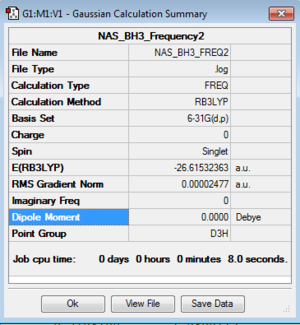
	Low frequencies --- -0.2268 -0.0081 -0.0006 22.1146 22.1157 24.1362 Low frequencies --- 1163.1747 1213.2735 1213.2737

NBO

Energy file DOI:10042/104583

BBr₃

B3LYP/6-31G(d,p)LANL2DZ level

Optimisation log file here or DOI:10042/93114

summary data	convergence	Jmol
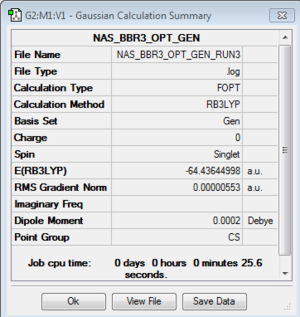
	Item Value Threshold Converged? Maximum Force 0.000011 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000047 0.001800 YES RMS Displacement 0.000031 0.001200 YES	optimised BH molecule

GaBr₃

B3LYP/LanL2DZ Level

Optimisation log file here or DOI:10042/88033

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000203 0.000450 YES RMS Force 0.000098 0.000300 YES Maximum Displacement 0.000867 0.001800 YES RMS Displacement 0.000415 0.001200 YES	optimised GaBr molecule

Frequency log file here or DOI:10042/101735

summary data	low modes
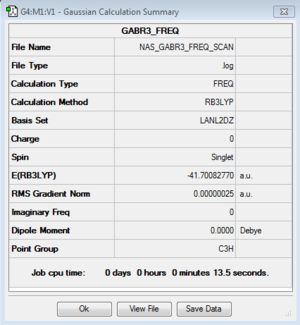
	Low frequencies --- -1.4878 -0.0015 -0.0002 0.0096 0.6540 0.6540 Low frequencies --- 76.3920 76.3924 99.6767

Optimisation Analysis

A bond is formed by the overlap of electron wavefunctions or atomic orbitals (of correct symmetry and similar energies) between atoms which interact to form new molecular orbitals which result in the overall lowering in potential energy of the molecule. Strong bonds arise when there is a significant interaction, and therefore lowering in energy, of AOs which occurs when the AOs are of similar energy and have high density. An example is a homodiatomic covalent bond such as C-C. A medium strength bond could be a heterodiatomic covalent bond of large atoms where there is a difference in energy of the AOs and hence the overlap is less efficient, resulting in a smaller lowering in energy than with the homodiatomic. For example, I-Se bond (mismatch in diffuse orbital’s size). The weakest bonds in this picture are those where there is only transient overlap of AOs, for example hydrogen bonding liquid water where thermal motion is continuously forming and breaking the weak bonds. We will use this basis to comment on our results below. NB: when interpreting bonds in Gaussview we need to remember the caveat that Guassview uses a predefined distance criteria to mark on bonds. (Similarly, most people use some predefinition of their own when drawing bonds with pen and paper- organic chemists draw c-c bonds all the time, but do not always painstakingly mark on hydrogen bonds….) BH3, BBr3 and GaBr3 are all trigonal planar complexes with an electron deficient group 13 element at their core. Naturally the bond length increases as Ga and Br are substituted for B and H respectively, as these heavier elements have larger valance orbitals. B-Br and Ga-Br bonds are formed via overlap of electron wavefunctions, and the sharing of electron density between the atoms contribute to forming a minimum on the potential energy surface. Ga-Br is the combination with the largest valance orbitals and hence we see that the bond equilibrium point occurs at a greater interatomic distance, whereas boron and hydrogen have valance orbitals with primary quantum number=1 and 2 respectively so form the shortest covalent bonds we studied. Additionally the strength of the bond is dependent on the size of the central atom, with the Ga valence orbitals being larger and more diffuse than the B orbitals, any overlap with ligand orbitals is less efficient and hence the stabilisation energy from the interaction is smaller in magnitude. B-Br bonds have a degree of double bond character, whereas B-H are singular in nature. Using a hybrid orbital approach, we consider B to be sp2 hybrid with a vacant pz orbital out of plane with the molecule. In B-H, this orbital remains unaffected by mixing since H does not possess any orbitals low enough in energy and of the correct symmetry to interact with it. However Br has a lone pair occupying the 4pz orbital. The interaction between these pz orbitals leads to a lowering of energy of molecule and forms a MO that smears some of the Br electron density towards the electron deficient B, hence a bond order above 1 is presence. A bond is formed by the overlap of electron wavefunctions or atomic orbitals (of correct symmetry and similar energies) between atoms which interact to form new molecular orbitals which result in the overall lowering in potential energy of the molecule.

Vibrational Analysis

Vibrational Analysis of BH₃

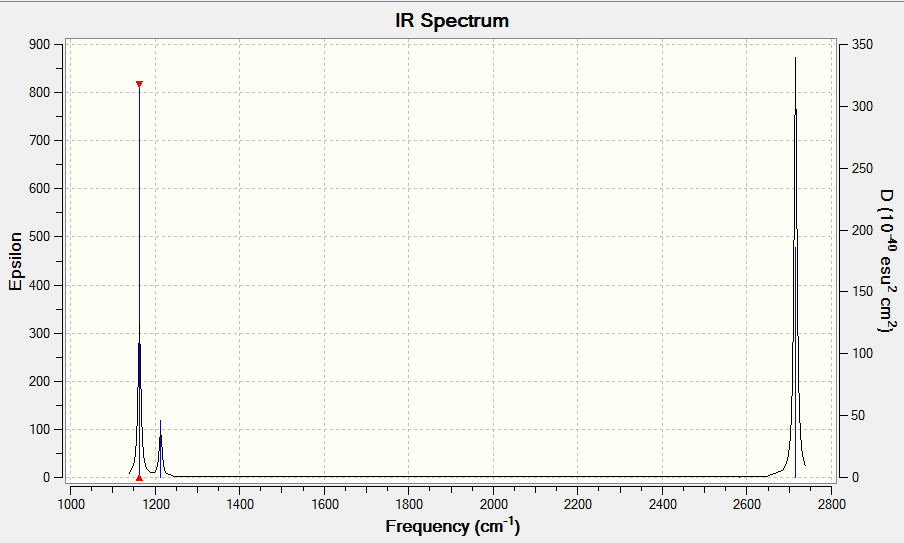
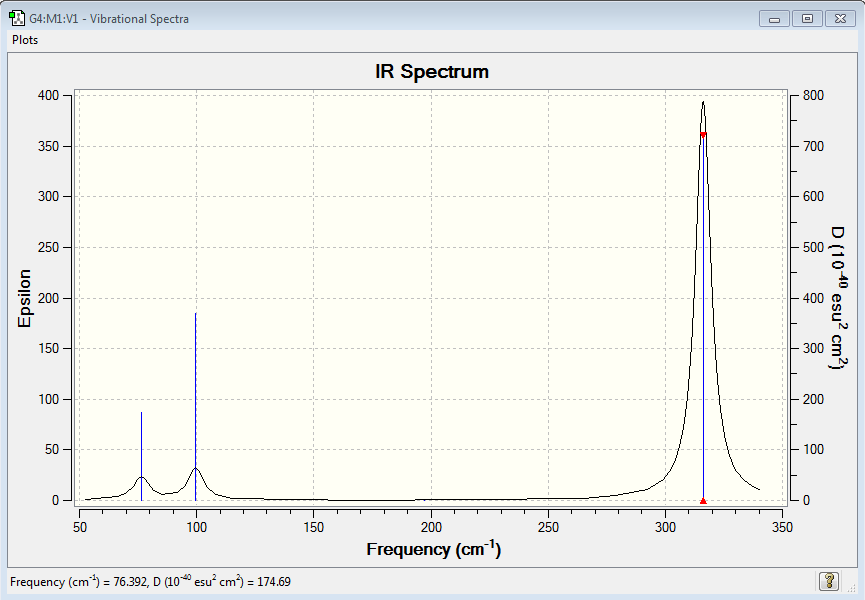
BH3 and GaBr3 both have 6 vibrational modes, in accordance with the 3N-2 rule. Moreover, both only have 3 visible peaks on the IR spectra. The modes at 2582 cm-1 on BH3 and at 197 cm-1 on GaBr3 are symmetric stretches which result in no change in dipole moment so are not IR active. We also note from our calculations that each molecule possess two sets of degenerate vibrational modes (1 set of bends and 1 of stretches per molecule). This means they reinforce each other on the spectra. It is also fruitful to note that the asymmetric stretch, whilst being more energetic in nature, also produce a greater intensity signal in the IR Spectrum due to the more pronounced change in dipole moment. GaBr3 has vibrational modes of a much less energetic nature than BH3. This reflects the fact that the Ga-Br bond is weaker (therefore the spring constant is smaller) and also the masses of the ligands are much larger. As a consequence the energy required to excite the molecule to the first vibrational mode is much less than required for the stronger, shorter B-H bond. We also notice that, especially for the A2’’ umbrella mode, that the Ga centre has a greater displacement along the z axis than B does in borane. This can be simply explained by the notion that the molecule is being considered in the centre of mass frame, so in order to conserve the CoM the central atom migrates in the opposite direction to the ligands. Since Ga makes up a much smaller fraction (less than ¼) of total mass of the molecule, there is a much greater displacement compared to Boron. The same basis set and methods are used when calculating frequencies and optimisations so we can draw a meaningful comparison between the molecules. Being inconsistent with frequency/optimisation calculations would lead to spurious results because of the difference in calculation methods using different potential energy surfaces. The purpose of carrying out frequency analysis, is mainly to confirm that we have reached a global energy minima. If all of our frequencies are positive it shows we have found a minimum, whereas if one or more are negative it shows we lie on a saddle on the potential energy surface and we have not acquired a fully optimised structure. The calculation also provides information about the vibrational modes of the molecules which we can compare our generated modes with those observed in experiment. The low frequencies show the movements of the centre of mass away from the equilibrium positions. We would expect these to relatively small otherwise this is signalling a large translational movement of the central (more massive atom).

wavenumber	Intensity	IR active?	type
1163	93	yes	bend
1213	14	weak	bend
1213	14	weak	bend
2582	0	no	symmetric stretch
2715	126	yes	asymmetric stretch
2715	126	yes	asymmetric stretch

Vibrational Analysis of GaBr₃

wavenumber	Intensity	IR active?	type
76	3	weak	bend
76	3	weak	bend
100	9	yes	bend
197	0	no	symmetric stretch
316	57	yes	asymmetric stretch
316	57	yes	asymmetric stretch

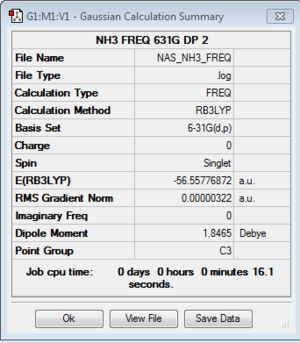
NH₃

B3LYP/6-31G(d,p)Level

Optimisation log file here or DOI:10042/104984

summary data	convergence	Jmol
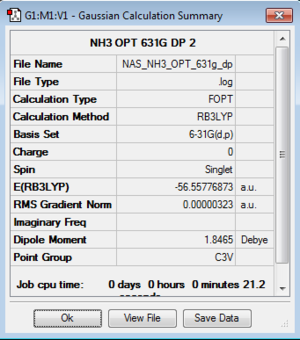
	Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES	optimised NH molecule

Frequency log file here or DOI:10042/105000

summary data	low modes
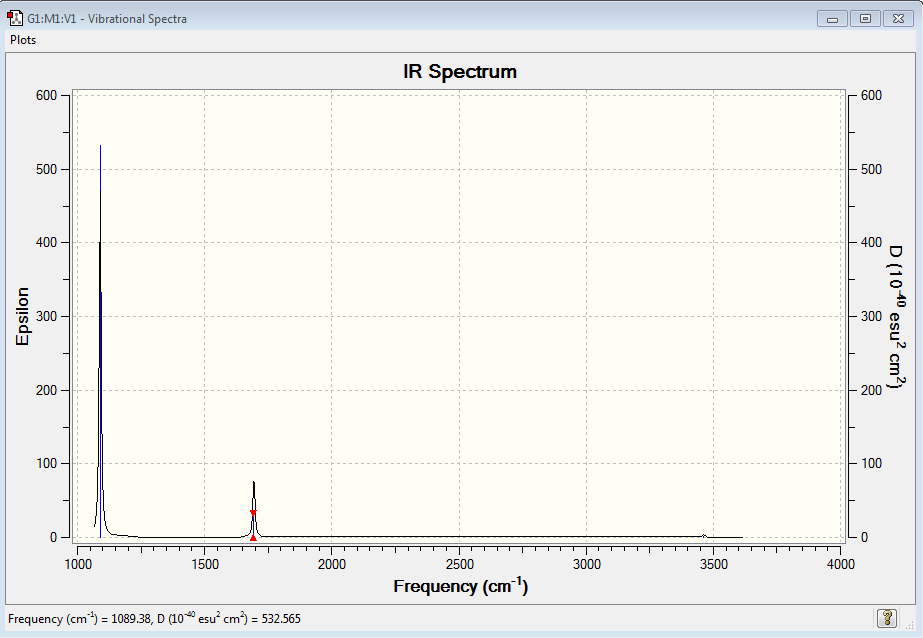
	Low frequencies --- -0.0138 -0.0026 -0.0009 7.0783 8.0932 8.0937 Low frequencies --- 1089.3840 1693.9368 1693.9368

Vibrational Analysis of NH₃

INSERT EXPLANATION OF WHY CERTAIN PEAKS SHOW UP AND WHY DEGENERACY

wavenumber	Intensity	IR active?	type
1089	145	strong	bend
1694	14	weak	bend
1694	14	weak	bend
3461	1	weak	symmetric stretch
3590	0	no/weak	asymmetric stretch
3590	0	no/weak	asymmetric stretch

NBO

Energy file DOI:10042/105042

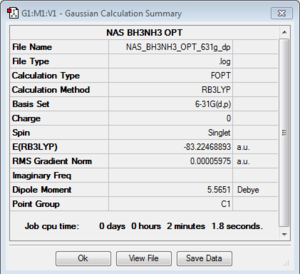
NH₃BH₃

B3LYP/6-31G(d,p)Level

Optimisation log file here or DOI:10042/106796

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000122 0.000450 YES RMS Force 0.000058 0.000300 YES Maximum Displacement 0.000513 0.001800 YES RMS Displacement 0.000296 0.001200 YES	optimised BHNH molecule

Frequency log file DOI:10042/106827

summary data	low modes
	Low frequencies --- -0.0251 -0.0032 -0.0007 17.1421 17.1447 37.2025 Low frequencies --- 265.8016 632.2134 639.3555

Vibrational Analysis of NH₃BH₃

wavenumber	Intensity	IR active?	type
266	0.0000	no	bend
632	14	weak	stretch
639	4	weak	bend
639	4	weak	bend
1069	41	Yes	bend
1069	41	Yes	bend
1196	110	yes	bend
1204	3	weak	bend
1204	3	weak	bend
1330	114	yes	bend
1676	28	yes	bend
1676	28	yes	bend
2470	67	yes	stretch
2530	231	yes	stretch
2530	231	yes	stretch
3462	3	weak	stretch
3580	28	yes	stretch
3580	28	yes	stretch

Energy of stabilisation of ammonia lp donation to borane

ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]=-83.2246889+56.5577687+26.6153235=-0.0515967 au -0.0515967*2625.50 (au->kjmol^-1 conversion factor) =-135.47 kjmol^-1

As we can see the donation of the ammonia lone pair into the electron deficient borane p_z orbital produces a stark lowering in energy of the system compared to the two isolated molecules. The value of -135 kj/mol is in line with weak covalent bonds, such as I-I (148kj/mol), however we expect at room temperature the bond is readily formed as the enthalpy of bond formation would overcome the reduction in entropy of the molecule. We also note the change of geometry of the BH₃ molecule to more of a tetrahedral-like structure. This can be rationalised by the change in hybridisation from sp² to sp³.

Comparison of LCAO and MO

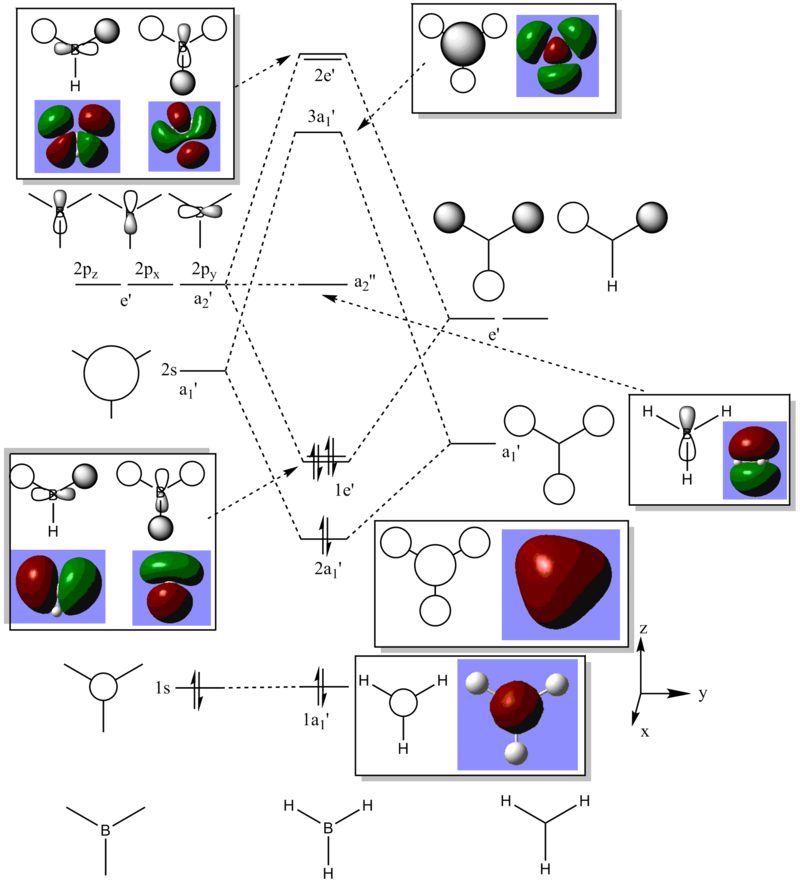
The similarity between the calculated MOs and the hand drawn AOs is striking. Not only do the LCAO predict the areas of opposite polarity and the correct nodal planes, but with a little imagination they correspond well to the through-space interactions which are fully incorporated in the MO calculation. For example the 1e’ orbitals show that there is significant electron density in between the LCAO representation, but this could have been guessed from the LCAO representation.

AROMATICITY PROJECT

Log Files on DSpace

Files Published on DSpace

Calculation	Benzene	Boratabenzene	Pyridinium	Borazine
Optimisation	DOI:10042/107118	DOI:10042/107249	DOI:10042/107337	DOI:10042/107464
Frequency	DOI:10042/107150	DOI:10042/107289	DOI:10042/107372	DOI:10042/107494
Energy	DOI:10042/107203	DOI:10042/107313	DOI:10042/107399	DOI:10042/107517

Optimisation Summaries

B3LYP/6-31G(d,p)Level

Molecule	summary data	convergence	Jmol
Benzene		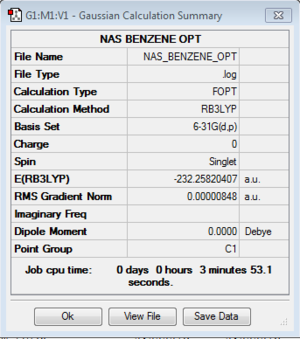Item Value Threshold Converged? Maximum Force 0.000013 0.000015 YES RMS Force 0.000004 0.000010 YES Maximum Displacement 0.000054 0.000060 YES RMS Displacement 0.000017 0.000040 YES Predicted change in Energy=-1.965794D-09 Optimization completed. -- Stationary point found.	optimised benzene molecule
Boratabenzene		Item Value Threshold Converged? Maximum Force 0.000011 0.000015 YES RMS Force 0.000002 0.000010 YES Maximum Displacement 0.000045 0.000060 YES RMS Displacement 0.000012 0.000040 YES Predicted change in Energy=-6.280187D-10 Optimization completed. -- Stationary point found.	optimised boratobenzene molecule
Pyridinium		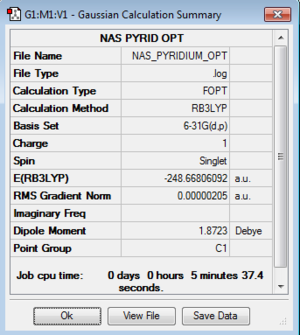Item Value Threshold Converged? Maximum Force 0.000004 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000010 0.000060 YES RMS Displacement 0.000004 0.000040 YES Predicted change in Energy=-9.102519D-11 Optimization completed. -- Stationary point found.	optimised pyridinium molecule
Borazine		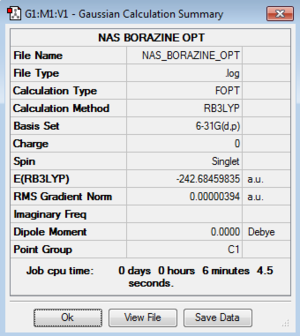Item Value Threshold Converged? Maximum Force 0.000008 0.000015 YES RMS Force 0.000002 0.000010 YES Maximum Displacement 0.000028 0.000060 YES RMS Displacement 0.000010 0.000040 YES Predicted change in Energy=-4.874603D-10 Optimization completed. -- Stationary point found.	optimised borazine molecule

Frequencies

Table showing Freq. Calc settings and "Low Frequency" values

Molecule	Summary	Low Frequencies
Benzene		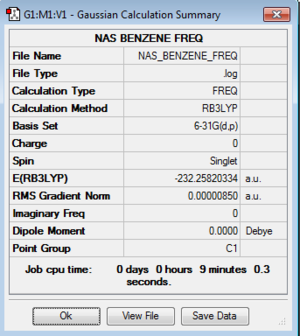Low frequencies --- -5.0211 -4.6278 -0.0005 0.0004 0.0009 3.2465 Low frequencies --- 414.5375 414.5498 621.0653
Boratobenzene		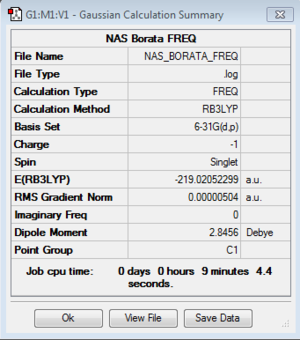Low frequencies --- -7.2623 -0.0008 -0.0003 0.0005 3.1684 4.5341 Low frequencies --- 371.2962 404.4164 565.0824
Pyridinium		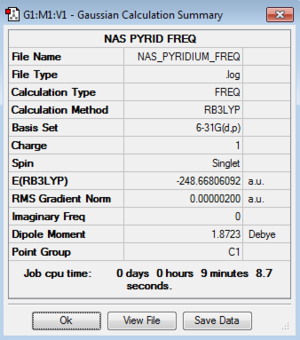Low frequencies --- -9.3855 -2.9634 -0.0006 -0.0003 0.0006 0.8971 Low frequencies --- 391.9002 404.3426 620.1994
Borazine		Low frequencies --- -8.1276 -2.9521 0.0005 0.0008 0.0011 5.9497 Low frequencies --- 289.5749 289.6524 404.4430

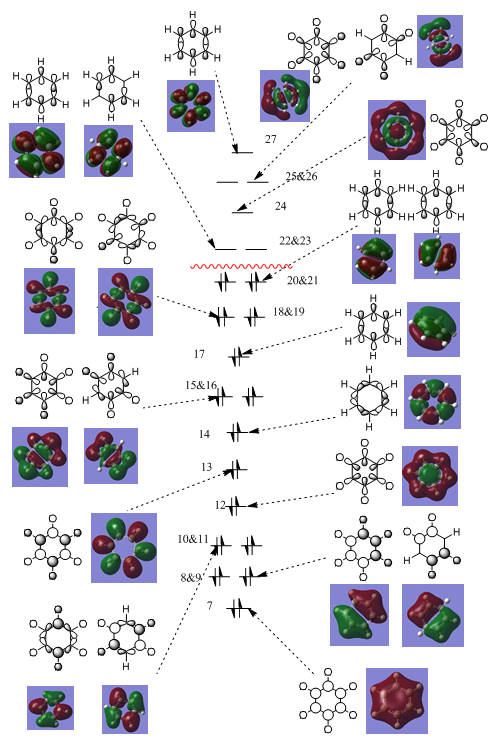
Simplified Molecular Orbital Diagram of Benzene

The following diagram compares the LCAO orbital representation and the molecular orbitals produced from calculation. There is a strong similarity between the two representations, paying testament to the validity of the LCAO approximation for molecular orbitals. The molecular orbital diagram can be split into those which contribute to the sigma framework and those that contribute to the out of plane π network, namely orbitals 17, 20-23 inclusive and 27. The sigma framework comprises of the MOs that are low in energy (7-17 and 18-19) and are responsible for the stability of the C-H bonds and much of the stability of the C-C bonds. The π network is formed from the overlap of the carbon p^z orbitals. The lowest energy π MO (17) presents a ring of delocalised electrodensity that only possesses 1 nodal plane. The next degenerate set of π orbitals again present an area of delocalised electrodenisty, however there is a second nodal plane which bisects the ring and divides two regions of opposite polarisation. Now we have established that there is a delocalised п system present the other condition for aromaticity is the electron occupation. To ensure that only the bonding orbitals are occupied we know that a п system must contain 4n+2 electrons. We find this Huckel Criteria is fulfilled as there are 6 electrons present and therefore benzene can be confirmed as aromatic.

NBO ANALYSIS

Table showing colour and numeric representations of charge distribution

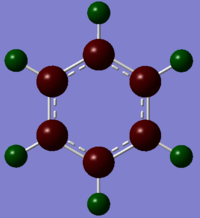
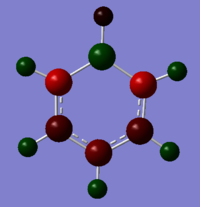
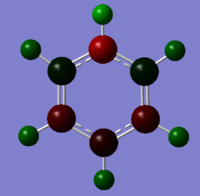
Type	Benzene	Boratabenzene	Pyridinium	Borazine
Colour Charge Representation
Numeric Charge Representation

Please note the range of the coloured representation is normalised to between -1 and 1 for ease of comparison.

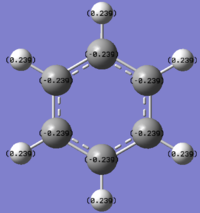
Firstly we note that in benzene the carbon atoms have a higher charge density and the hydrogens. This is because carbon is more electronegative than hydrogen due to its higher effective nuclear charge, so the bonding orbitals containing the electrons contain more carbon orbital character and have more density on the carbon than the hydrogen. We should also note due to the high level of symmetry (D6h) all carbons have the same relative charge and likewise so do all hydrogen atoms.

Boron is less electronegative than hydrogen and even less electronegative than carbon. This means that there is a lesser contribution to the bonding MOs from boron than carbon, and a greater contribution to the anti-bonding orbitals. As a consequence the boron atom is positively charged (0.208) and the neighbouring carbons are more negatively charged than in benzene. This largely down to effects on the sigma framework rather than the π network, because the sigma network orbitals of boron are in plane so have a larger amount of density closer to carbon atoms. We also note that the carbon para to the boron atom is more negatively charged than in benzene as the electropositive boron pushes electron density across the ring.

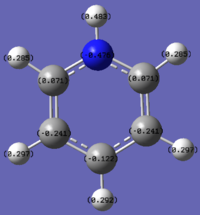
Pyridinium contains the electronegative Nitrogen atom. This contributes to a greater extent to the low energy bonding orbitals and hence there is greater electron density associated with the negatively charged Nitrogen. In the reverse case to boratabenzene the carbons adjacent to nitrogen are relatively positive, due to their proximity to the nitrogen. The para carbon is slightly less negative than may be expected when compared to benzene, this can be explained by invoking resonance structures of the pyridinium in which the para and meta carbons can hold a localised positive charge.

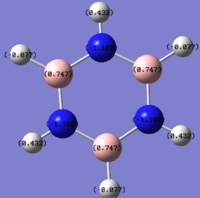
Borazine demonstrates a mixture of these effects. The electronegativity difference between the boron and nitrogen is greater than any of the previous comparisons and as a consequence the magnitude of the charges is at a greater scale. Essentially at this point the molecule is becoming less delocalised with a large part of the electrodensity situated on the nitrogens and their adjacent hydrogens.

MO comparison

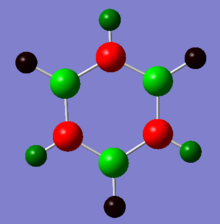
Clockwise from top left: benzene, boratobenzene, pyridinium and borazine

This set makes up part of the c-c sigma framework. As we can see the symmetry is a key factor is the shape of these orbitals, with both benzene and borazine showing the same shaped MO. However more interestingly the MO in the boratobenzene orbitals curl away from boron since it is electropositive. And likewise the orbitals curl towards the electronegative nitrogen.

Clockwise from top left: benzene, boratobenzene, pyridinium and borazine