Rep:Title=Mod:ELMI

Inorganic Computational

Objectives

To use computational techniques and carry out simple calculations with the aim to learn more about small molecules including optimising structures and predicting IR spectra.

Part 1

Optimising the structure of molecules

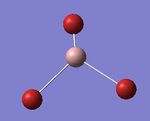
Analysing the optimised BH₃

A molecule of BH₃ was created on Gaussian 5.0. The bond lengths were manually set at 1.53,1.54 and 1.55 Å. An optimisation calculation was run on the same program using the 3-21G basis set. The resulting bond angles and lengths were found to be 120.0 ^o and 1.19 Å, respectively. This is an expected result for BH₃, which has the D_3h symmetry group. More information, including the final energy, can be seen in Table 1.

**Table 1** Optimisation of BH₃ using 3-21G
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	3-21G
Final energy (a.u.)	-26.4622429
Gradient (a.u.)	0.00008851
Dipole moment (D)	0.00
Point group	C_s
Calculation time (s)	20.0

   Item               Value     Threshold  Converged?
 Maximum Force            0.000220     0.000450     YES
 RMS     Force            0.000106     0.000300     YES
 Maximum Displacement     0.000940     0.001800     YES
 RMS     Displacement     0.000447     0.001200     YES
 Predicted change in Energy=-1.672479D-07
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.1948         -DE/DX =   -0.0002              !
 ! R2    R(1,3)                  1.1947         -DE/DX =   -0.0002              !
 ! R3    R(1,4)                  1.1944         -DE/DX =   -0.0001              !
 ! A1    A(2,1,3)              120.0157         -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              119.986          -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              119.9983         -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------

Please find the corresponding .log file here

3-21G is considered a small basis set and it was desirable to use more functions to describe the electronic structure. Therefore, the 6-31G(d,p) basis set was chosen since it uses d and p-orbital functions. Again the bond angles and lengths were recorded and found to equal 120.0 ^o and 1.19 Å. These are the same results as when using the 3-21G basis set. The bond lengths were slightly smaller when looking past two decimal places however this calculation is known to only be accurate to 0.01 Å.

**Table 2** Optimisation of BH₃ using 6-31G(d,p)
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy (a.u.)	-26.61532358
Gradient (a.u.)	0.00008206
Dipole moment (D)	0.00
Point group	C_s
Calculation time (s)	16.0

Item               Value     Threshold  Converged?
 Maximum Force            0.000204     0.000450     YES
 RMS     Force            0.000099     0.000300     YES
 Maximum Displacement     0.000875     0.001800     YES
 RMS     Displacement     0.000418     0.001200     YES
 Predicted change in Energy=-1.452109D-07
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.1928         -DE/DX =   -0.0002              !
 ! R2    R(1,3)                  1.1926         -DE/DX =   -0.0002              !
 ! R3    R(1,4)                  1.1924         -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0146         -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              119.9866         -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              119.9988         -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------

Please find the corresponding .log file here

Using psuedo-potentials and larger basis sets

A molecule of GaBr₃ was created and optimised in a similar way to BH₃. However, during this calculation the symmetry point group was set as D_3h and the LANL2DZ basis set was chosen, which is a medium level basis set that includes psuedo-potentials for heavier atoms such as gallium and bromine. As well, additional words such as "opt=tight" and "int=ultrafine" were added to the calculation to ensure the molecule was optimised. The results can be seen in Table 3 and the resulting bond angles and lengths were 120 ^o and 2.35 Å. The calculated bond lengths are concordant with a trigonal planar molecule and the bond lengths show good agreement with the literature's 2.33 Å ^[1].

**Table 3** Optimisation of GaBr₃ using a medium level basis set
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	LANL2DZ
Final energy (a.u.)	-41.70082783
Gradient (a.u.)	0.00000016
Dipole moment (D)	0.00
Point group	D_3h
Calculation time (s)	10.0

Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000003     0.000060     YES
 RMS     Displacement     0.000002     0.000040     YES
 Predicted change in Energy=-1.297295D-12
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  2.3502         -DE/DX =    0.0                 !
 ! R2    R(1,3)                  2.3502         -DE/DX =    0.0                 !
 ! R3    R(1,4)                  2.3502         -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------

Please find the corresponding .log file here

A similar calculation was run on a molecule of BBr₃, with the results in Table 4. The Gen basis set allows the basis set for each individual atom to be decided. In this case, 6-31G(d,p) was chosen for boron but LanL2DZ was used for the bromine atoms, which means pseudo-potentials are being used on the heavier atoms. The bond angles and lengths were found to be 120 ^o and 1.93 Å for all B-Br bonds.

**Table 4** Optimisation of BBr₃
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	Gen
Final energy (a.u.)	-64.43644960
Gradient (a.u.)	0.00000486
Dipole moment (D)	0.00
Point group	C_s
Calculation time (s)	35.0

Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000015     YES
 RMS     Force            0.000005     0.000010     YES
 Maximum Displacement     0.000049     0.000060     YES
 RMS     Displacement     0.000030     0.000040     YES
 Predicted change in Energy=-2.970801D-10
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.9339         -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.934          -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.9339         -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0007         -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0012         -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              119.9981         -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------

Please find the corresponding .log file here

↑ O. da Silva, O. Proux, J-L. Hazeman, J. James-Smith, D. Testemale and T. Yamaguchi, "X-ray Absorption Spectroscopy Study of Solvation and Ion-Pairing in aqueous Gallium Bromide Solutions at Supercritical Conditions", Journal of Molecular Liguds, 2008, 147, 83-95 DOI:10.1016/j.molliq.2008.06.022

Comparing bond lengths

Since all molecules BH₃, GaBr₃ and BBr₃ showed an optimised bond angle of 120 ^o it was much more interesting to compare their optimised bond lengths as summarised in Table 5. The BH₃ and BBr₃ bond lengths also show good agreement with literature values ^[1]^[2]. When the ligands are compared it can be seen that the B-Br bond is 62 % longer than the B-H bond. This can be rationalised since bromine is in the third row of the periodic table and substantially heavier than hydrogen. This means bromine has a larger atomic radius with the possibility of populating p- and d-orbitals. However, bromine is more electronegative compared to hydrogen, which suggests a more polar bond with boron and would lead to a decrease in bond length due to the increased ionic character. It is obvious that the increased size of bromine is the dominating factor since a bond elongation is observed when hydrogen is replaced by bromine in BH₃.

It was also possible to compare bond lengths when the central atom was changed. Gallium is bigger than boron since it is in the same period as bromine. Therefore an increase in bond length is expected and was observed as around a 22 % increase. Since bromine and gallium are in the same period they have similar atomic radii with gallium's being slightly larger due to the trend of atomic radius decreasing along a period. However, there will be better orbital overlap between the boron and bromine. This is because for gallium the available orbitals, 4p, are more diffuse compared to boron's 2p. Worse orbital overlap leads to weaker and therefore longer bonds. The bromine will also form a polar bond with gallium due to the difference in electronegativities however this is not believed to be a determining factor in the optimised bond length.

It was sometimes observed that Gaussview did not always show bonds between the atoms in these simple molecules. This is not because they were not present but because Gaussview determines the existence of bonds based on the distance between atoms only. In reality, many other factors must be considered however it is generally considered that a bond is formed when there is a net attraction between atoms. For a more conclusive approach of whether a bond has formed or not it is advantageous to look at molecular orbital theory.

Table 5 Comparing bond lengths
Molecule	Bond length (Å)
BH₃	1.19
GaBr₃	2.35
BBr₃	1.93

↑ H. B. Gray, "Chemical Bonds: an introduction to atomic and molecular structure", University Science Books, 1994, 2nd edition, 115
↑ John Wiley and Sons "Ullmann's Fine Chemicals", Wiley-VCH, 2013, 346

Frequency calculations

A frequency calculation is considered the second derivative of a potential energy surface and it also allows vibrational modes to be understood, which can then be used to compare computational and experimental IR and Ramen spectra.

BH₃ frequency calculations

This calculation was carried out using the same program as above on the optimised molecule of BH₃ using the same basis set of 6-31G(d,p) and with D_3h symmetry imposed on the molecule. The results can be seen below in Table 6 and below that are two lines titled Low frequencies. These frequencies refer to the 3N-6 vibrational modes present in the molecule. The first line refers to the movements of the centre of mass of the molecule, which in this case is the central boron atom and should ideally be as close to zero as possible however frequencies of +/- 15 cm^-1 were accepted as being a successful calculation. The second line of Low frequencies are large and positive, another sign that the calculation worked.

**Table 6** Frequency of BH₃ using 6-31G(d,p)
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy (a.u.)	-26.61532364
Gradient (a.u.)	0.00000215
Dipole moment (D)	0.00
Point group	D_3h
Calculation time (s)	5.0

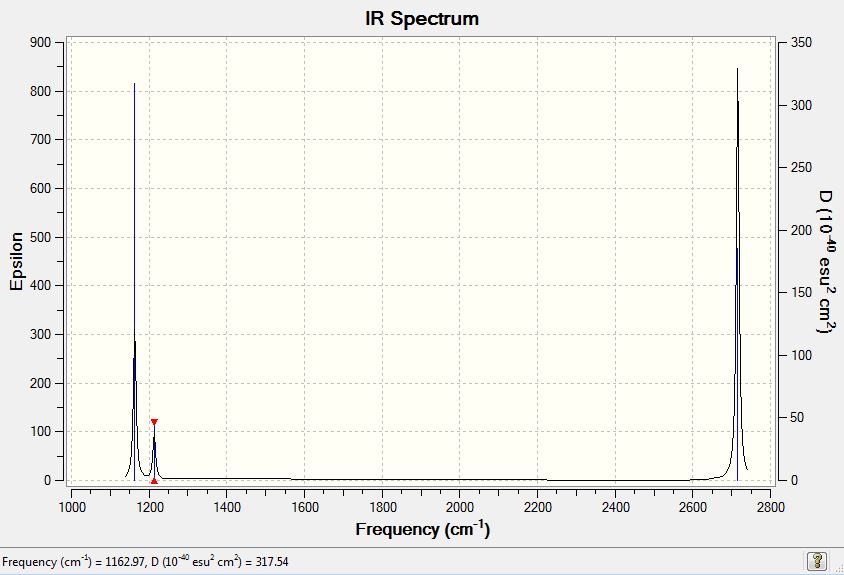
Low frequencies ---  -11.7227  -11.7148   -6.6070   -0.0004    0.0278    0.4278
 Low frequencies --- 1162.9743 1213.1388 1213.1390

Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000002     0.000300     YES
 Maximum Displacement     0.000017     0.001800     YES
 RMS     Displacement     0.000008     0.001200     YES
 Predicted change in Energy=-1.087480D-10
 Optimization completed.
    -- Stationary point found.

Please find the corresponding .log file here

Below shows a summary of the vibrational modes of BH₃ with the atom labels shown here.

Table 7
Vibrational Mode Number	Vibration Frequency (cm^-1)	Description	Intensity	Symmetry D_3h point group
1	1163	All hydrogens wagging in time with the boron atom moving up as the hydrogens move down and vice versa	93	A2"
2	1213	Three hydrogens moving in plane of molecule and boron atom stationary, 3H and 4H rocking and 2H scissoring with respect to them	14	E'
3	1213	3H and 4H scissoring in plane of molecule with boron and 2H stationary	14	E'
4	2583	All three hydrogens moving in plane of molecule at the same time, symmetrical stretching	0	A'
5	2716	Asymmetrical stretching of 3H and 4H in plane of molecule	126	E'
6	2716	Symmetrical stretching of 3H and 4H and asymmetrical stretching of 2H with respect to them	126	E'

Six peaks are expected in the IR spectrum due to the number of vibrational modes predicted however only three peaks can be seen above. This is due to the overlap of vibrational modes 2 and 3 and then 5 and 6. Each of these vibrational modes have a degenerate symmetry point group (E'). Vibrational mode 4 is IR inactive due to the symmetrical stretching of all three hydrogens and so no corresponding peak is seen in the spectrum. The three peaks in the calculated IR spectrum were found to be 1163, 1213 and 2715 cm^-1. These frequencies show good agreement with the literature's 1148, 1198 and 2602 cm^-1^[1].

↑ K. Kawaguchi, J. E. Butler, C. Yamada, S. H. Bauer, T. Minowa, H. Kahamon and E. Hirota, "Observation of the gas-phase infrared spectrum of BH₃", Journal of Chemical Physics, 1987, 87, 2438 DOI:10.1063/1.453135

GaBr₃ frequency calculations

The same method used for BH₃ was applied on the optimised molecule of GaBr₃. The lowest real frequency was found to be 76 cm^-1.

**Table 8** Frequency of GaBr₃
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	LANL2DZ
Final energy (a.u.)	-41.70082770
Gradient (a.u.)	0.00000021
Dipole moment (D)	0.00
Point group	D_3h
Calculation time (s)	7.0

Low frequencies ---   -1.4877   -0.0015   -0.0002    0.0096    0.6540    0.6540
 Low frequencies ---   76.3920   76.3924   99.6767

Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000004     0.000060     YES
 RMS     Displacement     0.000002     0.000040     YES
 Predicted change in Energy=-2.185815D-12
 Optimization completed.
    -- Stationary point found.

Please find the corresponding .log file here

Below shows a summary of the vibrational modes of GaBr₃ with the atom labels shown here.

Table 9
Vibrational Mode Number	Vibration Frequency (cm^-1)	Description	Intensity	Symmetry D_3h point group
1	76	3Br and 4Br scissoring in plane of molecule with 2Br stationary, gallium has small displacement vector so moves slightly, same as vibrational mode 3 of BH₃	3	E'
2	76	3Br and 4Br rocking and 2Br scissoring with respect to them, same as vibrational mode 2 of BH₃	3	E'
3	100	All three bromines moving together in and out of plane with gallium moving in the opposite direction, same as vibrational mode 1 of BH₃	9	A2"
4	197	All three bromines moving in plane of molecule at the same time, symmetrical stretching, same as vibrational mode 4 of BH₃	0	A1'
5	316	Symmetrical stretching of 3H and 4H and asymmetrical stretching of 2H with respect to them, same as vibrational mode 6 of BH₃	57	E'
6	316	Asymmetrical stretching of 3Br and 4Br in plane of molecule, same as vibrational mode 5 of BH₃	57	E'

The spectrum above shows three peaks with frequencies 76, 100 and 316 cm^-1. This is lower than the six vibrational modes recorded in Table 9 for similar reasons as BH₃ such as degenerate vibrational modes (1 and 2 and then 5 and 6) and IR inactive symmetrical stretches. The predicted frequencies show good agreement with the literature's 89, 100 and 355 cm^-1 ^[1]

↑ N. N. Greenwood, "Spectroscopic Properties of Inorganic and Organometallic Compounds; Volume 9", RSC, 1976, 198

Comparing the frequencies of BH₃ and GaBr₃

Table 10 Comparing frequencies of BH₃ and GaBr₃
Vibrational Mode	BH₃ frequency (cm^-1)	GaBr₃ frequency (cm^-1)
1	1163	76
2	1213	76
3	1213	100
4	2583	197
5	2716	316
6	2716	316

It can be seen that BH₃ has much larger frequency values compared GaBr₃. This is due to both gallium and bromine being heavier atoms than boron and hydrogen. The frequency value is inversely proportional to the reduced mass of a molecule in the Harmonic Oscillator equation ( $υ = \frac{1}{2 π c} \sqrt{\frac{k}{μ}}$ ). Therefore the heavier the molecule the smaller the stretching frequency. Also as previously discovered in the previous section the B-H bond is stronger compared to the Ga-Br bond, which will also lead to an increase in the frequency values. There has also been a change in the order for the lower energy frequencies of both molecules. The E' degenerate modes for BH₃ correspond to the vibrational modes 2 and 3 however in GaBr₃ these are found at vibrational modes 1 and 2.

The spectra of both molecules share the same shape with only three peaks observed. BH₃ GaBr₃ are both trigonal planar molecules with D_3h point group symmetry therefore the same vibrational modes are expected. As previously explained only three peaks are observed for each molecule for the same reasons; degeneracy and symmetrical stretching. However the spectra do not show any similarities in intensities. The shape of each spectrum shows one peak at high energy and two peaks at lower energies. When the animations were viewed on Gaussview 5.0 it could be seen that the higher energy A₁' and E' vibrational modes corresponded to stretching frequencies whereas the lower energy vibrational modes were bending modes. It is obvious that more energy is required to cause a stretching mode since this refers to a change in bond length rather than a change in bond angle as for bending modes.

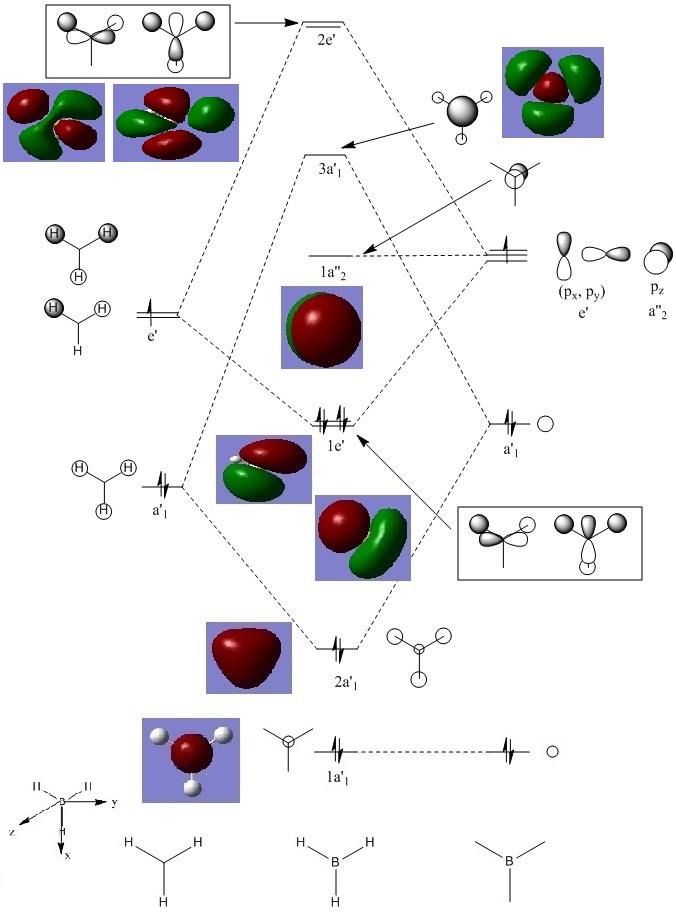
BH₃ MO diagram

The optimised molecule output (checkpoint file) was used to analyse the molecular orbitals (MOs) of BH₃ using Gaussview and with the additional key words "pop=full". By placing the calculated MOs on top of the MO diagram below it can be seen that the calculated orbitals match up mostly with the predicted orbitals from LCAO (linear combination of atomic orbitals) theory. However for the more complex MOs it is better to use the computed orbitals to better understand their nature and shape. LCAO is unfortunately only a qualitative approach and so should be used in tandem with computational techniques to fully grasp the electronic structure and nature of a molecule.

**Table 11** Population analysis of BH₃ using 6-31G(d,p)
File type	.chk
Calculation type	SP
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy (a.u.)	-26.61532364
Gradient (a.u.)	0.0000000
Dipole moment (D)	0.00
Point group	D_3h
Calculation time (s)	5.0

Please find the corresponding .log file here

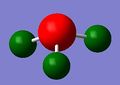
NH₃ NBO analysis

A molecule of NH₃ was optimised then frequency and population analyses were run in the same manner as for BH₃ and GaBr₃ however the additional key words "nosymm" were also included. The results below show that all calculations were successful.

**Table 12** Optimisation of NH₃ using 6-31G(d,p)
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy (a.u.)	-56.55776872
Gradient (a.u.)	0.00000314
Dipole moment (D)	1.85
Point group	C_s
Calculation time (s)	3.0

Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000030     YES
 RMS     Force            0.000004     0.000020     YES
 Maximum Displacement     0.000016     0.000120     YES
 RMS     Displacement     0.000011     0.000080     YES
 Predicted change in Energy=-1.165946D-10
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.018          -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.018          -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.018          -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              105.7446         -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              105.7446         -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              105.7445         -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)           -111.8637         -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------

Please find the corresponding .log file here

**Table 13** Frequency of NH₃ using 6-31G(d,p)
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy (a.u.)	-56.55776872
Gradient (a.u.)	0.00000314
Dipole moment (D)	1.85
Point group	C₃
Calculation time (s)	11.0

Low frequencies ---    0.0013    0.0019    0.0023    3.2004    6.2581    7.7429
 Low frequencies --- 1089.3668 1693.9325 1693.9356

Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000013     0.001800     YES
 RMS     Displacement     0.000007     0.001200     YES
 Predicted change in Energy=-1.074677D-10
 Optimization completed.
    -- Stationary point found.

Please find the corresponding .log file here

**Table 14** Population analysis of NH₃ using 6-31G(d,p)
File type	.chk
Calculation type	SP
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy (a.u.)	-56.55776874
Gradient (a.u.)	0.00000000
Dipole moment (D)	1.85
Point group	C_s
Calculation time (s)	5.0

Please find the corresponding .log file here

The NBO (natural bond orbital) charge distribution was then found using the .log output file of the population analysis. The output can be seen on the left with a charge range of -1.000 and +1.000. However it was more informative to use actual numbers, seen on the right. Now it can be seen that the sum of each individual NBO charge distribution is zero, confirming the neutrality of NH₃. Nitrogen has a large and negative charge distribution, which is seen in red in the first picture, and is expected.

NBO charge distribution of NH₃
Specific NBO charge distribution of NH₃

NH₃BH₃ Association Energies

A molecule of NH₃BH₃ was optimised and underwent a frequency analysis. The results can be seen below.

**Table 15** Optimisation of NH₃BH₃ using 6-31G(d,p)
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy (a.u.)	-83.22468908
Gradient (a.u.)	0.00000138
Dipole moment (D)	5.56
Point group	C₁
Calculation time (s)	57.0

Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000034     0.000060     YES
 RMS     Displacement     0.000010     0.000040     YES
 Predicted change in Energy=-1.180662D-10
 Optimization completed.
    -- Stationary point found.----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,7)                  1.0185         -DE/DX =    0.0                 !
 ! R2    R(2,7)                  1.0185         -DE/DX =    0.0                 !
 ! R3    R(3,7)                  1.0185         -DE/DX =    0.0                 !
 ! R4    R(4,8)                  1.2098         -DE/DX =    0.0                 !
 ! R5    R(5,8)                  1.2098         -DE/DX =    0.0                 !
 ! R6    R(6,8)                  1.2098         -DE/DX =    0.0                 !
 ! R7    R(7,8)                  1.6677         -DE/DX =    0.0                 !
 ! A1    A(1,7,2)              107.8749         -DE/DX =    0.0                 !
 ! A2    A(1,7,3)              107.8748         -DE/DX =    0.0                 !
 ! A3    A(1,7,8)              111.024          -DE/DX =    0.0                 !
 ! A4    A(2,7,3)              107.8749         -DE/DX =    0.0                 !
 ! A5    A(2,7,8)              111.0238         -DE/DX =    0.0                 !
 ! A6    A(3,7,8)              111.0241         -DE/DX =    0.0                 !
 ! A7    A(4,8,5)              113.874          -DE/DX =    0.0                 !
 ! A8    A(4,8,6)              113.8741         -DE/DX =    0.0                 !
 ! A9    A(4,8,7)              104.5971         -DE/DX =    0.0                 !
 ! A10   A(5,8,6)              113.8742         -DE/DX =    0.0                 !
 ! A11   A(5,8,7)              104.5971         -DE/DX =    0.0                 !
 ! A12   A(6,8,7)              104.5972         -DE/DX =    0.0                 !
 ! D1    D(1,7,8,4)           -179.9998         -DE/DX =    0.0                 !
 ! D2    D(1,7,8,5)            -59.9999         -DE/DX =    0.0                 !
 ! D3    D(1,7,8,6)             60.0002         -DE/DX =    0.0                 !
 ! D4    D(2,7,8,4)            -59.9998         -DE/DX =    0.0                 !
 ! D5    D(2,7,8,5)             60.0            -DE/DX =    0.0                 !
 ! D6    D(2,7,8,6)           -179.9998         -DE/DX =    0.0                 !
 ! D7    D(3,7,8,4)             60.0002         -DE/DX =    0.0                 !
 ! D8    D(3,7,8,5)           -179.9999         -DE/DX =    0.0                 !
 ! D9    D(3,7,8,6)            -59.9998         -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------

Please find the corresponding .log file here

**Table 16** Frequency of NH₃BH₃ using 6-31G(d,p)
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy (a.u.)	-83.22468909
Gradient (a.u.)	0.00000144
Dipole moment (D)	5.56
Point group	C₁
Calculation time (s)	30.0

Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000029     0.001800     YES
 RMS     Displacement     0.000011     0.001200     YES
 Predicted change in Energy=-1.303340D-10
 Optimization completed.
    -- Stationary point found.

Low frequencies ---   -2.1878   -0.0005   -0.0005    0.0004    2.3950    3.3005
 Low frequencies ---  263.4754  632.9559  638.4487

Please find the corresponding .log file here

The energies of BH₃, NH₃ and BH₃NH₃ were found to be -26.61532358, -56.55776872 and -83.22468909 a.u. respectively. By putting these numbers into this equation $Δ E = E (N H_{3} B H_{3}) - [E (N H_{3}) + E (B H_{3})]$ the energy difference or association energy of ammonium borane was found to be -0.05159679 a.u. A conversion factor of 2625.50^[1] was then used to convert this into kJmol^-1 and was found to equal -135.4673721. However due to accuracy restrictions this can only be recorded as -135 kJmol^-1. On the other hand, the bond dissociation is +135 kJmol^-1, which shows some agreement with the literature as it has the same order of magnitude^[2].

↑ See http://web.utk.edu/~rcompton/constants
↑ H. B. Gray, "Chemical Bonds: an introduction to atomic and molecular structure", University Science Books, 1994, 2nd edition, 115

Part 2: Main Group Halides

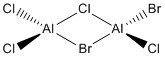
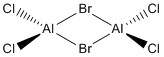
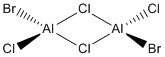
The aim of this section was to analyse the conformers and vibrations of a particular main group halide, Al₂Cl₄Br₂.

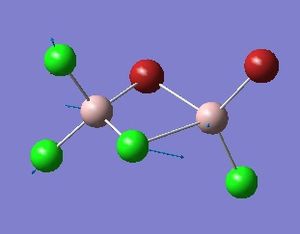
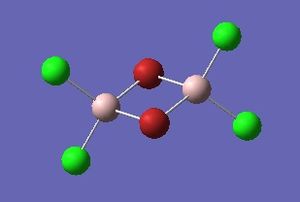
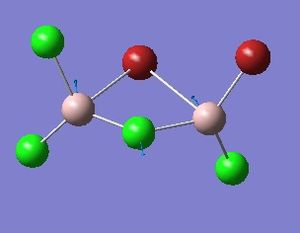
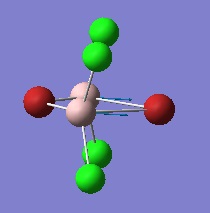
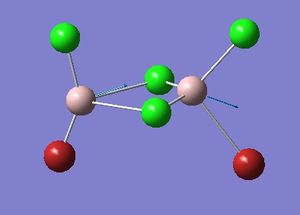
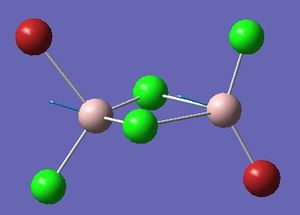
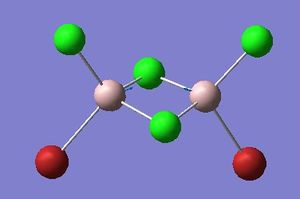
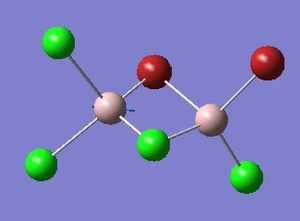
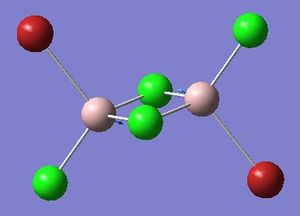
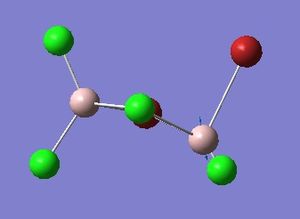
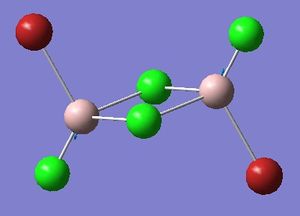
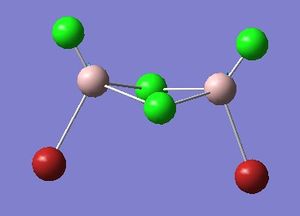
Optimisation of Four isomers of Al₂Cl₄Br₂

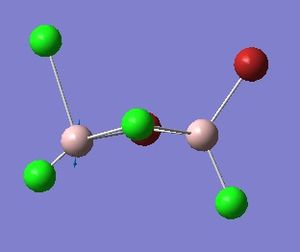
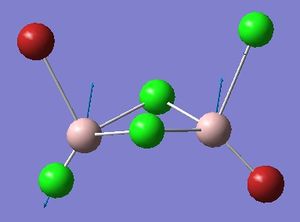
Four isomers of Al₂Cl₄Br₂ were optimised on Gaussview 5.0 using the 6-31G(d,p) basis set on the aluminium and chlorine atoms but a pseudo-potential (LANL2DZ) on the heavier bromine atoms. The results can be seen below, in Table 1 and the following Item tables show that each calculation was successful.

Isomer 1 optimisation

Item               Value     Threshold  Converged?
 Maximum Force            0.000023     0.000450     YES
 RMS     Force            0.000012     0.000300     YES
 Maximum Displacement     0.000641     0.001800     YES
 RMS     Displacement     0.000320     0.001200     YES
 Predicted change in Energy=-2.571159D-08
 Optimization completed.
    -- Stationary point found.

Please find the corresponding .log file here

Isomer 2 optimisation

Item               Value     Threshold  Converged?
 Maximum Force            0.000105     0.000450     YES
 RMS     Force            0.000026     0.000300     YES
 Maximum Displacement     0.001366     0.001800     YES
 RMS     Displacement     0.000597     0.001200     YES
 Predicted change in Energy=-1.133618D-07
 Optimization completed.
    -- Stationary point found.

Please find the corresponding .log file here

Isomer 3 optimisation

Item               Value     Threshold  Converged?
 Maximum Force            0.000003     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000040     0.001800     YES
 RMS     Displacement     0.000015     0.001200     YES
 Predicted change in Energy=-2.937156D-10
 Optimization completed.
    -- Stationary point found.

Please find the corresponding .log file here

Isomer 4 optimisation

Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000054     0.001800     YES
 RMS     Displacement     0.000024     0.001200     YES
 Predicted change in Energy=-6.158890D-10
 Optimization completed.
    -- Stationary point found.

Please find the corresponding .log file here

**Table 1** Optimisation of 4 isomers of Al₂Cl₄Br₂ using 6-31G(d,p) and LANL2DZ
	Isomer 1	Isomer 2	Isomer 3	Isomer 4

File type	.log	.log	.log	.log
Calculation type	FOPT	FOPT	FOPT	FOPT
Calculation method	RB3LYP	RB3LYP	RB3LYP	RB3LYP
Basis set	6-31G(d,p)	6-31G(d,p)	6-31G(d,p)	6-31G(d,p)
Final energy (a.u.)	-2352.41626573	-2352.41109930	-2352.40630798	-2352.41629861
Gradient (a.u.)	0.00001266	0.00003313	0.00000187	0.00000404
Dipole moment (D)	0.19	0.14	0.00	0.00
Point group	C₁	C₁	C₁	C₁
Expected point group	C_2v	C₁	D_2h	C_2h
Calculation time (s)	187	298	179	186

Table 2 shows the overall energies of each isomer in atomic units and were converted into kJmol^-1 using the same conversion factor as in Part 1. Unfortunately, due to the limits of accuracy provided by the program, energies recorded in kJmol^-1 can only be commented on to the closest 10 kJmol^-1. Therefore, it can be conclusively said that Isomers 2 and 3 are higher in energy compared to Isomers 1 and 4 but one cannot know which Isomer has the absolute lowest energy. However, upon examining the isomers it is probable that Isomer 4 is the lowest energy conformer. This is most likely due to the location of the bromine atoms, since they are the atoms in the molecule with the largest atomic radii, therefore in a trans conformation, as in Isomer 4, there is the least amount of steric hindrance and will lead to the lowest energy conformer. This is in agreement with the energies calculated in a.u.. Also, the dipole moment is minimised on Isomer 4 compared to Isomer 1.

The highest energy isomer has both bromine atoms in a bridging position and using the same argument above this is to be expected due to the large atomic radii of the bromine atoms. Additionally, the Al-Cl bonds will be stronger compared to the Al-Br bonds, due to better overlap since aluminium and chlorine are in the same period. This will be important since this molecule was imagined to be made upon dimerisation of AlCl₂Br and if two chlorines are in the bridging positions then there will be a stronger interaction between the monomers.

Table 2 Relative energies of each isomer
Isomer	1	2	3	4
Energy (a.u.)	-2352.41626573	-2352.41109930	-2352.40630798	-2352.41629861
Energy (kJmol^-1)	-6176268.906	-6176255.341	-6176242.762	-6176268.992
Relative energy compared to Isomer 4 (kJmol^-1)	0.08632644	13.65078841	26.23039907	0.00000000

Al₂Cl₄Br₂ dissociation energies

As previously mentioned it was envisaged that Al₂Cl₄Br₂ was made from two molecules of AlCl₂Br. An optimisation calculation of the monomer was conducted along with a frequency analysis to confirm that a minimum was reached. The same basis sets and key words were used as for Al₂Cl₄Br₂, in order to make useful comparisons. The results can be seen below:

Optimisation of AlCl₄Br:

Item               Value     Threshold  Converged?
 Maximum Force            0.000136     0.000450     YES
 RMS     Force            0.000073     0.000300     YES
 Maximum Displacement     0.000760     0.001800     YES
 RMS     Displacement     0.000497     0.001200     YES
 Predicted change in Energy=-7.984437D-08
 Optimization completed.
    -- Stationary point found.

**Table 3** Optimisation of AlCl₂Br using 6-31G(d,p)and LANL2DZ
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	Gen
Final energy (a.u.)	-1176.19013679
Gradient (a.u.)	0.00004196
Dipole moment (D)	0.11
Point group	C_2v
Calculation time (s)	16.0

Please find the corresponding .log file here

Frequency of AlCl₄Br:

Item               Value     Threshold  Converged?
 Maximum Force            0.000081     0.000450     YES
 RMS     Force            0.000042     0.000300     YES
 Maximum Displacement     0.001588     0.001800     YES
 RMS     Displacement     0.000974     0.001200     YES
 Predicted change in Energy=-1.810813D-07
 Optimization completed.
    -- Stationary point found.

Low frequencies ---   -0.0015    0.0022    0.0027    1.3569    3.6367    4.2604
 Low frequencies ---  120.5042  133.9178  185.8950

**Table 4** Frequency of AlCl₂Br using 6-31G(d,p)and LANL2DZ
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	Gen
Final energy (a.u.)	-1176.19013679
Gradient (a.u.)	0.00004194
Dipole moment (D)	0.11
Point group	C_2v
Calculation time (s)	9.0

Please find the corresponding .log file here

The overall energies of the lowest energy dimer (Isomer 4) and two monomers were then used to find $Δ E$ . This was found to equal -94.58 kJmol^-1 or -90 kJmol^-1 to the nearest 10 kJmol^-1. In other words the dissociation of energy of Isomer 4 into its monomers is +90 kJmol^-1 and therefore the product of Al₂Cl₄Br₂ is more stable than the isolated monomers, AlCl₂Br. This is expected when considering that AlCl₂Br is electron deficient in a similar way that AlCl₃ is and can gain electron density through forming dative bonds with another molecule of itself to form the more stable dimer.

Frequency analysis of four isomers of Al₂Cl₄Br₂

The optimised structures of the four isomers of Al₂Cl₄Br₂ underwent a frequency analysis using the same basis set and pseudo-potentials as used in the optimisation calculations. However, the key words "opt(maxcycle=50) were removed since the molecules had already been optimised. The results of the frequency calculations can be seen below. As in Part 1 the calculation can be deemed successful if the zero-frequencies are within +/- 15 cm^-1.

Isomer 1:

Low frequencies ---   -4.2536   -2.3935   -0.0023    0.0018    0.0022    1.2830
 Low frequencies ---   17.1620   50.9093   78.5490

**Table 5** Frequency of Al₂Cl₄Br₂ Isomer 1 using 6-31G(d,p) and LANL2DZ
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	Gen
Final energy (a.u.)	-2352.41626680
Gradient (a.u.)	0.00000697
Dipole moment (D)	0.17
Point group	C₁
Calculation time (s)	50.0

Please find the corresponding .log file here

Isomer 2:

Low frequencies ---   -2.9939   -1.4805    0.0006    0.0017    0.0026    3.0872
 Low frequencies ---   17.0191   55.9578   80.0486

**Table 6** Frequency of Al₂Cl₄Br₂ Isomer 2 using 6-31G(d,p) and LANL2DZ
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	Gen
Final energy (a.u.)	-2352.41109930
Gradient (a.u.)	0.00003312
Dipole moment (D)	0.14
Point group	C₁
Calculation time (s)	55.0

Please find the corresponding .log file here

Isomer 3:

Low frequencies ---   -5.1748   -5.0356   -3.1468    0.0012    0.0016    0.0028
 Low frequencies ---   14.8260   63.2702   86.0770

**Table 7** Frequency of Al₂Cl₄Br₂ Isomer 3 using 6-31G(d,p) and LANL2DZ
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	Gen
Final energy (a.u.)	-2352.40630798
Gradient (a.u.)	0.00000187
Dipole moment (D)	0.00
Point group	C₁
Calculation time (s)	54.0

Please find the corresponding .log file here

Isomer 4:

Low frequencies ---   -5.1490    0.0033    0.0038    0.0039    1.4146    2.0504
 Low frequencies ---   18.1472   49.1065   73.0086

**Table 8** Frequency of Al₂Cl₄Br₂ Isomer 3 using 6-31G(d,p) and LANL2DZ
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	Gen
Final energy (a.u.)	-2352.41629861
Gradient (a.u.)	0.00000408
Dipole moment (D)	0.00
Point group	C₁
Calculation time (s)	57.0

Please find the corresponding .log file here

The corresponding IR spectra can be seen below and can be clicked to enlarge each image or look to Table 9 for a summary of all important frequencies, where frequencies were recorded to the nearest cm^-1 and the numbers in brackets refer to the intensity of the peaks.

Isomer 1
Isomer 2
Isomer 3
Isomer 4

Table 9 Infrared frequencies (cm^-1) from each of the four Isomers of Al₂Cl₄Br₂
Isomer 1	Isomer 2	Isomer 3	Isomer 4
103 (3)	92 (1)	108 (5)	117 (9)
121 (13)	110 (5)	126 (8)	120 (13)
123 (6)	121 (8)	138 (7)	160 (6)
158 (5)	149 (5)	241 (100)	280 (29)
194 (2)	154 (6)	341 (161)	413 (149)
279 (25)	186 (1)	467 (347)	421 (439)
309 (2)	211 (21)	616 (332)	579 (316)
413 (149)	257 (10)
420 (411)	289 (48)
461 (35)	384 (154)
582 (278)	424 (274)
	493 (106)
	574 (122)
	615 (197)

Only peaks with an intensity value over 1 were recorded in Table 9 in order to compare the number of peaks in each of the IR spectra. It can be seen that Isomers 3 and 4 produced spectra with fewer bands, which suggests a higher level of symmetry in these isomers. This is expected to be the case since these particular isomers have high symmetry point groups, D_2h and C_2h respectively. Symmetrical stretching vibrations are not visible in IR spectra and are often called IR-inactive. More symmetrical molecules would be expected to produce more symmetrical stretching vibrations. In agreement with this argument, Isomer 2 produced the most number of peaks in its IR spectrum and has the lowest symmetry point group. On comparing the actual shapes of the IR spectra it was found that Isomers 1 and 4 produced very similar spectra. This is also expected from the previous analysis since both bromines are in terminal positions and they have related symmetry point groups, differing only in the direction of the reflection plane present.

Each molecule should give 18 vibrational modes, given by the equation $3 N - 6$ . This was found to be true when viewing the vibrations summary in Gaussview rather than the spectrum only. Many of these vibrational modes are not present in the spectra since they are symmetrical stretches. An advantage of computational techniques is that vibrational modes not found experimentally can be defined. For example, many peaks in the spectrum of Isomer 3 are not visible since all terminal atoms are the same and therefore many of the vibrational modes caused by rocking, twisting or wagging of the terminal chlorines (vibrational modes one to three, five to six and eight) are IR inactive. When comparing some of these vibrational modes with the other isomers it was found that, for example, vibrational mode 4 of Isomer 3 is in fact vibrational mode 3 in the other three isomers. This particular vibrational mode refers to the terminal atoms scissoring in unison with respect to the bridging chlorines and aluminium atoms. This means that even though each isomer has the same number of vibrational modes, they do not always correspond to the same motion for each isomer, which can be rationalised as a reordering of vibrational frequencies. This means a particular vibrational mode has changed frequency due to a change in atom position. For the example described above, the same motion in Isomer 3 is nearly double the frequencies compared to the other isomers. This may be due to stronger bonds being formed between aluminium and chlorine compared to aluminium and bromine and the fact Isomer 3 has all chlorines in terminal positions.

Al-Br vibrational frequencies

It was interesting to analyse specific Al-Br stretches considering the varying positions of the bromine atoms in the isomers, as in terminal versus bridging positions and cis versus trans conformations. To begin with the relevant vibrational modes for each isomer was identified in order to make applicable comparisons between the isomers.

Table 10: Specific vibrational modes of Isomers 2 and 3
Isomer 2				Isomer 3
Vibrational Mode Number	Image	Frequency (cm^-1)	Intensity	Vibrational Mode Number	Image	Frequency (cm^-1)	Intensity
11	Both aluminium oscillating in between terminal atoms to cause asymmetric stretching of aluminiums with respect to the bridging bromine	211	21	11	Both aluminium oscillating in between terminal atoms to cause asymmetric stretching of aluminiums with respect to the bridging bromine	197	0
12	Two aluminium fragments, chlorine and bromine bridging atoms moving in towards the molecule then out again in unison	257	10	12	Two aluminiums rocking symmetrically in and out between the terminal atoms causing symmetrical stretching of both bromine atoms with respect to each aluminium	441	98
13	Asymmetric stretching of aluminium with respect to bridging chlorine, which causes a small asymmetric stretching between the aluminiums and bridging bromine	289	48	13	Two aluminium fragments and bridging bromine atoms moving in towards the molecule then out again in unison, causes symmetrical stretching across whole molecule	247	0
14	Symmetric stretching of aluminiums with respect to bridging bromine atom	384	154	14	Two aluminiums oscillating side to side, which causes asymmetrical stretching of Al-Br bonds	341	161

Table 10 shows the interesting vibrational modes when bromine was in a bridging position. Some of the vibrational modes are the same in both Isomers 2 and 3, for example vibrational mode 11. For some of the vibrational modes there has been a reordering, as in the same vibrational mode is present for both isomers but has a different vibrational mode number. For example, vibrational mode 12 for Isomer 2 is the same motion as vibrational mode 13 for Isomer 3. However, for Isomer 3 this mode is IR-inactive and can not be seen in the spectrum above. This shows that computational methods can be used to calculate the frequencies of the same vibrational motions in two different isomers, even when one would not be visible experimentally. In fact, this particular motion has a very similar frequency value for both isomers although reordering has occurred.

Table 11: Specific vibrational modes of Isomers 1, 2 and 4
Isomer 1				Isomer 2				Isomer 4
Vibrational Mode Number	Image	Frequency (cm^-1)	Intensity	Vibrational Mode Number	Image	Frequency (cm^-1)	Intensity	Vibrational Mode Number	Image	Frequency (cm^-1)	Intensity
15	Both aluminiums rocking in between the terminal atoms causing antisymmetric stretching of Al-Br terminal bonds	419	411	15	Both aluminiums rocking in between the terminal atoms causing antisymmetric stretching but aluminium attached to terminal bromine moving much more	424	274	15	Both aluminiums rocking in between the terminal atoms causing antisymmetric stretching of Al-Br terminal bonds	421	439
16	Two aluminiums scissoring into middle of molecule causing symmetric stretching of Al-Br terminal bonds	461	35	16	Two aluminiums scissoring into middle of molecule causing symmetric stretching but aluminium attached to two terminal chlorines moving much more	493	106	16	Two aluminiums scissoring into middle of molecule causing symmetric stretching of Al-Br terminal bonds	459	0
17	Anti-symmetrical stretching of Al-Cl _terminal causes slight antisymmetric stretching of Al-Br	570	32	17	Symmetrical stretching of aluminiums with respect to trans chlorines, aluminium attached to terminal bromine moving much more	574	122	17	Same motion as in Isomer 1 vibrational mode 17 but now symmetrical stretching of Al-Br	574	0
18	Symmetric stretching of Al-Cl_terminal causes greater effective symmetrical stretching of Al-Br bonds	582	278	18	Asymmetric stretching of aluminiums with respect to terminal chlorines causing a small Al-Br stretch	615	197	18	Same motion as in Isomer 1 vibrational mode 18 but now asymmetrical stretching of Al-Br	579	316

Table 11 shows the interesting vibrations when bromine was in a terminal position. It was found that Isomers 1 and 4 had the same vibrational modes for each vibrational mode 14-18. Although the motions were the same, due to the cis versus trans positions of the terminal bromine atoms, the symmetry of the resulting stretches varied. For example, for vibrational mode 17 causes anti-symmetrical stretching of Al-Br bonds in Isomer 1 but symmetrical stretching for Isomer 4. No peak can be seen for Isomer 4 for this particular vibrational mode since it is symmetrical across the whole molecule and is therefore IR-inactive. The largest Al-Br stretch was definitely seen in vibrational mode 17 in Isomer 2, due to the aluminium atoms having very different vectors.

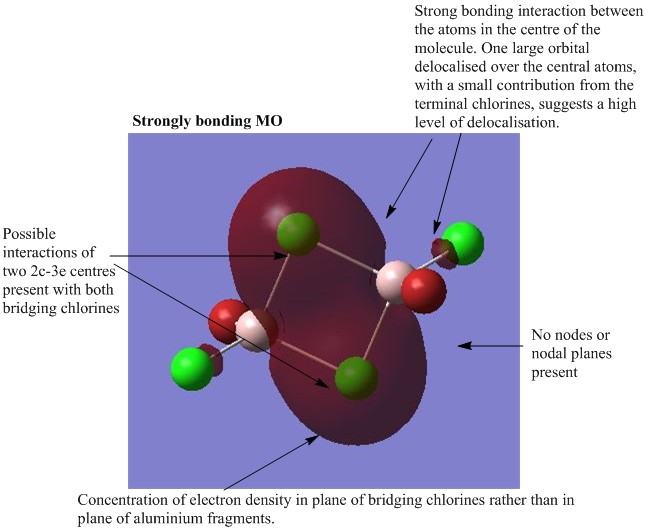
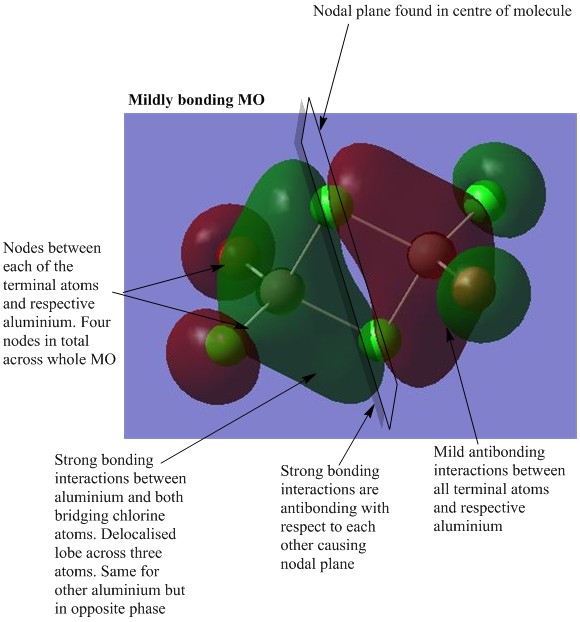
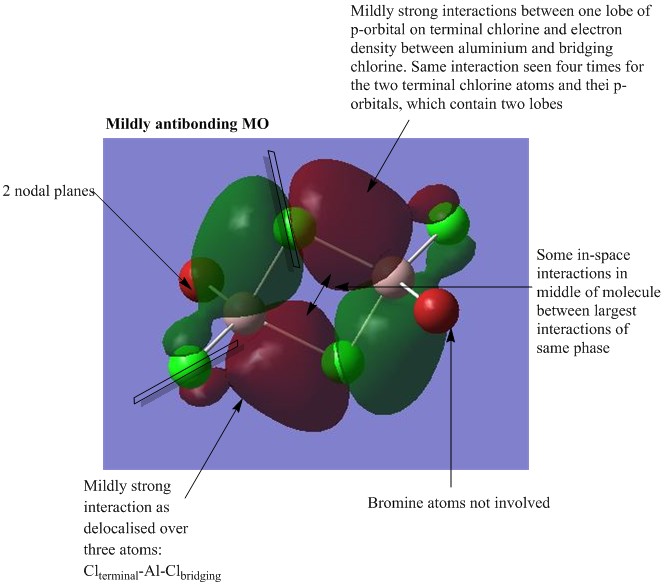
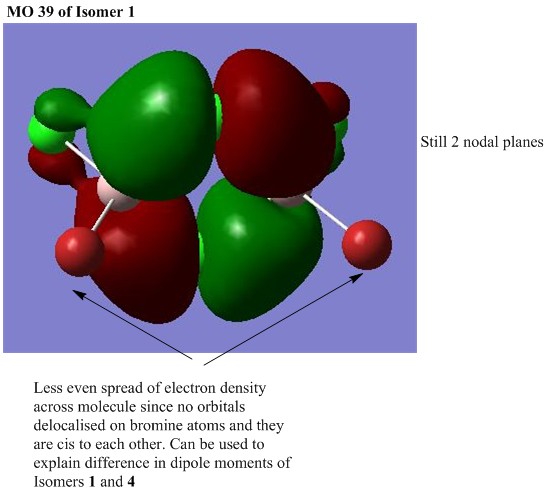
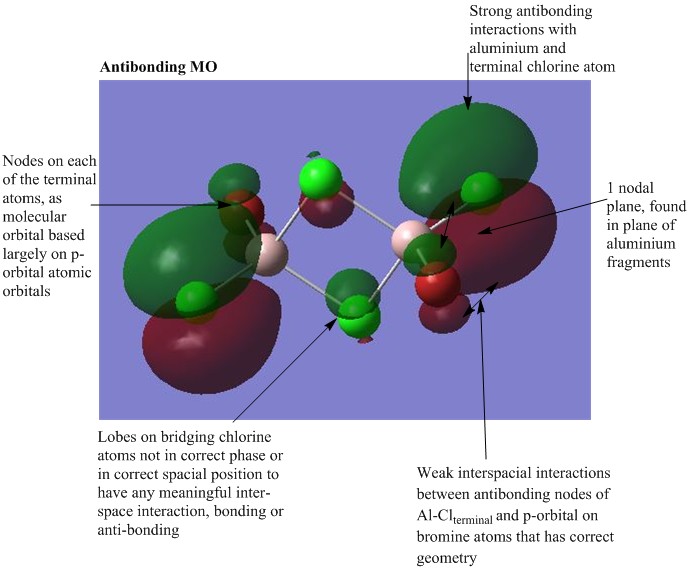
MO analysis of Isomer 4

The lowest energy isomer, Isomer 4, underwent a population analysis, with "pop=full" additional keywords, so that all of the occupied non-core molecular orbitals could be visualised. There was a large energy gap between the core and non-core orbitals present in this molecule and it was only considered interesting to visualise a handful of occupied non-core molecular orbitals with varying degrees of bonding. The chosen orbitals were numbers 31, 37, 39, 47 and 54 and the results can be seen below. One molecular orbital of Isomer 1 was also visualised in order to compare the effects of having the bromine atoms in trans versus cis positions. For each of the chosen molecular orbitals the interactions were described and evaluated.

Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000054     0.001800     YES
 RMS     Displacement     0.000024     0.001200     YES
 Predicted change in Energy=-6.158890D-10
 Optimization completed.
    -- Stationary point found.

**Table 12** Population Analysis of Al₂Cl₄Br₂ Isomer 4 using 6-31G(d,p) and LANL2DZ
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	Gen
Final energy (a.u.)	-2352.41629861
Gradient (a.u.)	0.00000404
Dipole moment (D)	0.0
Point group	C₁
Calculation time (s)	246

Please find the corresponding .log file here

For Isomer 1 comparison

Item               Value     Threshold  Converged?
 Maximum Force            0.000011     0.000450     YES
 RMS     Force            0.000006     0.000300     YES
 Maximum Displacement     0.001031     0.001800     YES
 RMS     Displacement     0.000407     0.001200     YES
 Predicted change in Energy=-5.099013D-09
 Optimization completed.
    -- Stationary point found.

**Table 13** Population analysis of Al₂Cl₄Br₂ Isomer 1 using 6-31G(d,p) and LANL2DZ
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	Gen
Final energy (a.u.)	-2352.41626680
Gradient (a.u.)	0.00000697
Dipole moment (D)	0.17
Point group	C₁
Calculation time (s)	32.0

Please find the corresponding .log file here

[elm1716-1] O. da Silva, O. Proux, J-L. Hazeman, J. James-Smith, D. Testemale and T. Yamaguchi, "X-ray Absorption Spectroscopy Study of Solvation and Ion-Pairing in aqueous Gallium Bromide Solutions at Supercritical Conditions", Journal of Molecular Liguds, 2008, 147, 83-95 DOI:10.1016/j.molliq.2008.06.022

[elm1111-2] H. B. Gray, "Chemical Bonds: an introduction to atomic and molecular structure", University Science Books, 1994, 2nd edition, 115

[elm3131-3] John Wiley and Sons "Ullmann's Fine Chemicals", Wiley-VCH, 2013, 346

[elm13-4] K. Kawaguchi, J. E. Butler, C. Yamada, S. H. Bauer, T. Minowa, H. Kahamon and E. Hirota, "Observation of the gas-phase infrared spectrum of BH₃", Journal of Chemical Physics, 1987, 87, 2438 DOI:10.1063/1.453135

[elm1-5] N. N. Greenwood, "Spectroscopic Properties of Inorganic and Organometallic Compounds; Volume 9", RSC, 1976, 198

[6] See http://web.utk.edu/~rcompton/constants

[elm1111-7] H. B. Gray, "Chemical Bonds: an introduction to atomic and molecular structure", University Science Books, 1994, 2nd edition, 115

[1]

[1]

[2]

[1]

[1]

[1]

[2]

Inorganic Computational

Objectives

Part 1

Optimising the structure of molecules

Analysing the optimised BH3

Using psuedo-potentials and larger basis sets

Comparing bond lengths

Frequency calculations

BH3 frequency calculations

GaBr3 frequency calculations

Comparing the frequencies of BH3 and GaBr3

BH3 MO diagram

NH3 NBO analysis

NH3BH3 Association Energies

Part 2: Main Group Halides

Optimisation of Four isomers of Al2Cl4Br2

Al2Cl4Br2 dissociation energies

Frequency analysis of four isomers of Al2Cl4Br2

Al-Br vibrational frequencies

MO analysis of Isomer 4

Analysing the optimised BH₃

BH₃ frequency calculations

GaBr₃ frequency calculations

Comparing the frequencies of BH₃ and GaBr₃

BH₃ MO diagram

NH₃ NBO analysis

NH₃BH₃ Association Energies

Optimisation of Four isomers of Al₂Cl₄Br₂

Al₂Cl₄Br₂ dissociation energies

Frequency analysis of four isomers of Al₂Cl₄Br₂