Rep:Title=Mod:ChlorineDJN16

ammonia

optimisation

optimised information

Calculation Method = RB3LYP

Basis Set = 6-31G(d,p)

E(RB3LYP) = -56.55776873 a.u.

RMS Gradient Norm = 0.00000485 a.u.

Point Group = C3V

bond length (N-H) = 1.01798Å

bond angle (H-N-H) = 105.741°

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES
 Predicted change in Energy=-5.986273D-10
 Optimization completed.
    -- Stationary point found.

optimised NH₃

optimised NH3

optimisation file for NH₃ is linked here

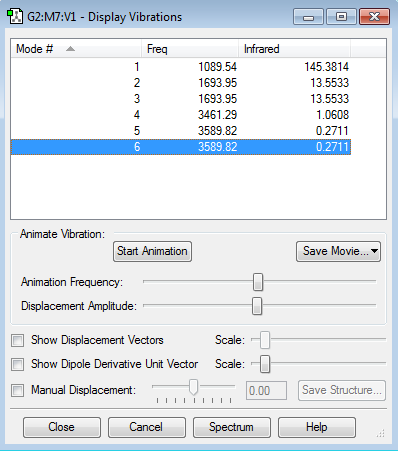
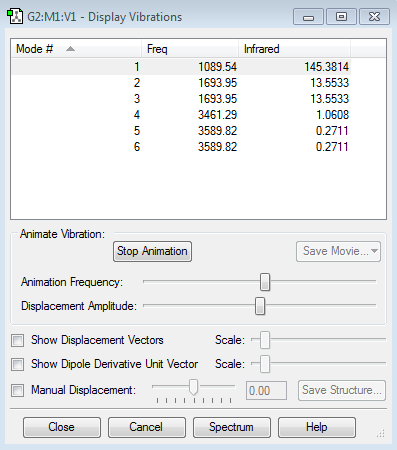
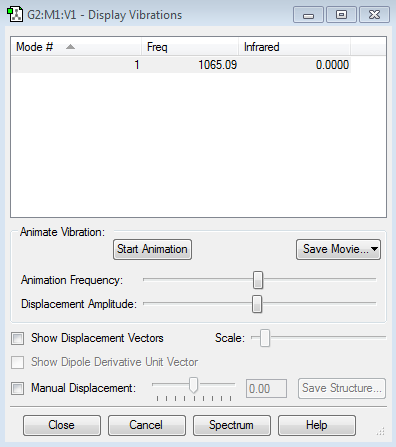
Vibrational modes

Questions: 1. How many modes of vibration are expected from the 3N-6 rule? 2. Which modes are degenerate? 3. Which modes are bending? which are stretching? 4. Which modes are highly symmetric? 5. Which mode is described as 'umbrella' mode? 6. How many main peaks should you expect to see in a spectrum for gaseous ammonia?

Ammonia can absorb IR because it has a dipole moment. Ammonia should show six vibrational modes. The bends 2&3 are degenerate and the stretches 5&6 are degenerate because the movements are symmetrical but the protons that are bending/stretching are different. Mode 4 is highly symmetric. Mode 1 is 'umbrella'. The two main peaks in the spectrum are due to mode 1 modes 2/3 (there are also two minuscule peaks due to modes 4 and 5/6)

types of vibrational mode

number of mode	description
1	umbrella, symmetric mode, bend
2	bend
3	bend
4	symmetric, stretch
5	stretch
6	stretch

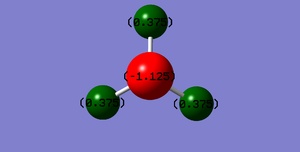
Charge distribution

Nitrogen has a higher charge density than the Hydrogen's because it is more electronegative. This gives the Nitrogen a partial negative charge and the Hydrogen's a partially positive charge

Nitrogen

optimisation

optimised information

Calculation Method = RB3LYP

Basis Set = 6-31G(d,p)

E(RB3LYP) = -109.52412868

RMS Gradient Norm = 0.00000060 a.u.

Point Group = D*H

bond length (N-N) = 1.10550Å

bond angle (N-N) = 180°

         Item             Value        Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES
 Predicted change in Energy=-3.383662D-13
 Optimization completed.
    -- Stationary point found.

optimised N₂

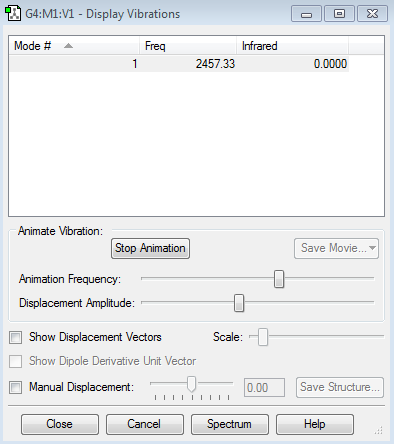
There are no IR peaks for N₂ because there is no dipole moment.

optimised N2

optimisation file for N₂ is linked here

in a diatomic molecule there is no relative charge on either atom.

Hydrogen

optimisation

Calculation Method = RB3LYP

Basis Set = 6-31G(d,p)

E(RB3LYP) = -1.17853936 a.u.

RMS Gradient Norm = 0.00000017 a.u.

Point Group = D*H

bond length (H-H) = 0.74279Å

bond angle (H-H) = 180°

         Item             Value        Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES
 Predicted change in Energy=-1.167770D-13
 Optimization completed.
    -- Stationary point found.

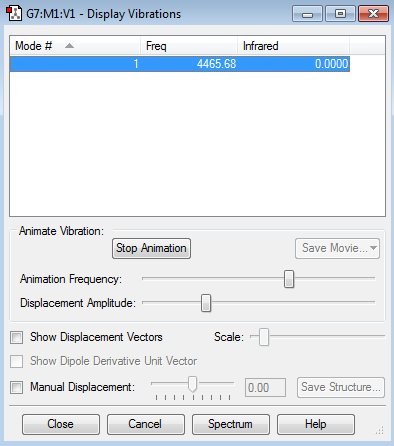
There are no IR peaks for H₂ because there is no dipole moment.

optimised H2

optimised H2

in a diatomic molecule there is no relative charge on either atom.

optimisation file for H₂ is linked here

Haber-Bosch process

N₂ + 3H₂ -> 2NH₃

E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.1155375 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 a.u.
ΔE= -146.478599028kJ/mol

literature value for haber bosch process: ΔH = -45.7kJ/mol.

The value of ΔE for the computed values is lower than the literature value

Fluorine

optimised information

Calculation Method = RB3LYP

Basis Set = 6-31G(d,p)

E(RB3LYP) = -199.49825218 a.u.

RMS Gradient Norm = 0.00007365 a.u.

Point Group = D*H

bond length (F-F) = 1.40281Å

bond angle (F-F) = 180°

         Item             Value        Threshold  Converged?
 Maximum Force            0.000128     0.000450     YES
 RMS     Force            0.000128     0.000300     YES
 Maximum Displacement     0.000156     0.001800     YES
 RMS     Displacement     0.000221     0.001200     YES
 Predicted change in Energy=-1.995024D-08
 Optimization completed.
    -- Stationary point found.

optimised F2

optimisation file for F₂ is linked here

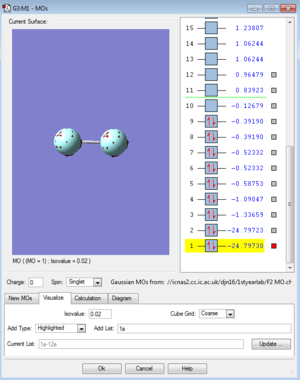
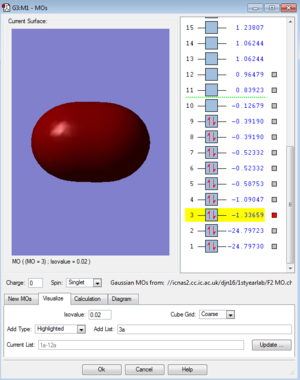
MOs for F₂

This is the molecular orbital (MO) that corresponds to the σ_1s MO of the F₂ molecule. The MO has energy of -24.79730 a.u. An energy this deep results in no overlap of the orbitals ad shown in the diagram.

This is the molecular orbital that corresponds to the σ_2s MO of the F₂ molecule. The MO has energy of -1.33659 a.u. This is a very symmetrical and stable MO formed by the overlap of electrons the 2s atomic orbitals of each Fluorine atom.

This is the molecular orbital that corresponds to the σ^*_2s MO of the F₂ molecule. The MO has energy of -1.09047 a.u. This MO is also formed by the overlap of electrons the 2s atomic orbitals of each Fluorine atom but this time they are in opposite phase. This σ^*_2s MO means that the σ_2s MO will not contribute the the bonding in the F₂ molecule as the antibonding orbital cancels the bonding orbital out.

This is the molecular orbital that corresponds to the σ_{z 2p} MO of the F₂ molecule. The MO has energy of -0.58753 a.u. This MO is formed by the overlap of the 2p_z electrons. It has the lowest energy MO of the MOs formed by the overlap of the 2p atomic orbitals. It's antibonding MO is unfilled therefore the F₂ can exist, but F₂ is a very volatile molecule and exists easily in radical form.

This is the molecular orbital that corresponds to the π_{2 px} MO of the F₂ molecule. The MO has energy of -0.52332 a.u. This MO is formed by the overlap of the 2p_z electrons. The π bond is formed by the overlap of the 2p electrons.

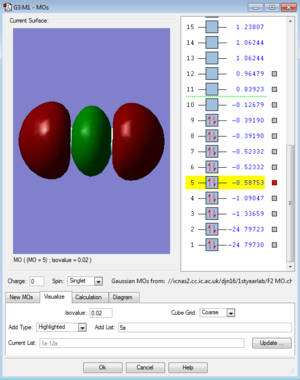
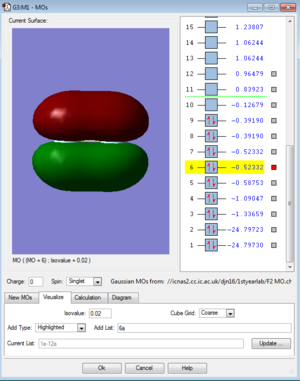
References

<references>