Rep:Title=Mod:19SAXON

NH₃ Molecule

Calculation Method:

RB3LYP

Basis Set:

6-31G(d,p)

Final Energy, E(RB3LYP) (au):

-56.55776873

RMS Gradient (au):

0.00000485

Point Group:

C3V

N-H Bond Length (au):

1.01798

H-N-H Bond Angle (deg):

105.741

Item Table

        Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

Optimisation file link

NH3

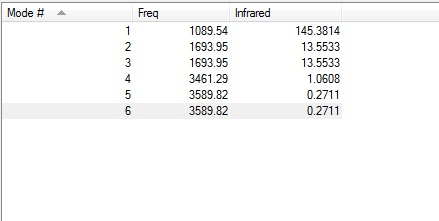
Vibrations

Questions:

-How many modes do you expect from the 3N-6 rule?

6 modes would be expected.

-Which modes are degenerate?

Modes 2,3 and 5, 6 are degenerate.

-Which modes are "bending" vibrations and which are "bond stretch" vibrations?

Bending: 1, 2, 3 Stretching: 4, 5, 6

-Which mode is highly symmetric? Mode 4 is highly symmetric.

-Which mode is known as the "umbrella" mode?

Mode 1 is the "umbrella" mode.

-How many bands would you expect to see in an experimental spectrum of gaseous ammonia?

You would expect to see 2 bands in the spectrum because mode 4 is highly symmetric and there is no change in dipole moment. Whilst there is a change in dipole moment for modes 5 and 6 the intensities are so low that they cannot be seen in a spectrum.

Charge Analysis

N atom charge= -1.125

H atom charge= +0.375

This is what was expected considering the high electronegativity of nitrogen compared to hydrogen.

N₂ Molecule

Calculation Method:

RB3LYP

Basis Set:

6-31G(d,p)

Final Energy, E(RB3LYP) (au):

-109.52412868

RMS Gradient (au):

0.00000060

Point Group:

D*h

N-N Bond Length (au):

1.10550

Item Table

         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES

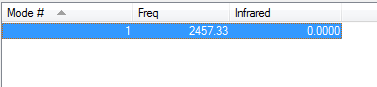
Vibrations

H₂ Molecule

Calculation Method:

RB3LYP

Basis Set:

6-31G(d,p)

Final Energy, E(RB3LYP) (au):

-1.17853936

RMS Gradient (au):

0.00000017

Point Group:

D*h

H-H Bond Length (au):

0.74279

Item Table

 Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES

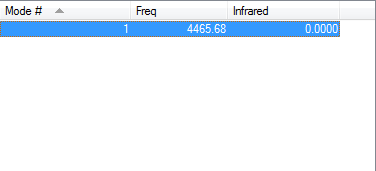
Vibrations

Reaction Energies

The reaction energy (ΔE) is being calculated for the reaction: N2 + 3H2 -> 2NH3

(au) E(NH3)=-56.55776873

2*E(NH3)=-113.11553746

E(N2)=-109.52412868

E(H2)=-1.17853936

3*E(H2)=-3.53561808

ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=-0.0557907

ΔE(KJ/mol)=-146.48

Compared to the literature value for Std enthalpy change of formation= −45.92 kJ/mol (for one NH3), =-91.84KJ/mol. (From: Cox, J.D.; Wagman, D.D.; Medvedev, V.A., CODATA Key Values for Thermodynamics, Hemisphere Publishing Corp., New York, 1984, 1)

The differences between the calculated value and the literature value stem from the limitations of the calculation. The calculation doesn't take into account thermodynamic considerations or rotational or vibrational energies.

BH₄^- Molecule

Calculation Method:

RB3LYP

Basis Set:

6-31G(d,p)

Final Energy, E(RB3LYP) (au):

-27.24992701

RMS Gradient (au):

0.00000671

Point Group:

TD

B-H Bond Length (au):

1.23933

H-B-H Bond Angle (deg):

109.471

Item Table

 Item               Value     Threshold  Converged?
 Maximum Force            0.000013     0.000450     YES
 RMS     Force            0.000007     0.000300     YES
 Maximum Displacement     0.000065     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

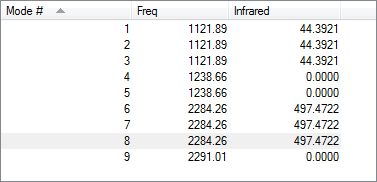
Vibrations

Two peaks would be expected in the experimental gaseous spectrum for BH4-. This is because of the degeneracy of modes 1-3 and 6-8. All other modes are inactive as due to their highly symmetric nature leading to no change in dipole moment.

Charge Analysis

N atom charge= -0.615

H atom charge= -0.096

This is what was expected considering the overall charge of the molecule.

Optimisation file link

BH4-

Molecular Orbitals

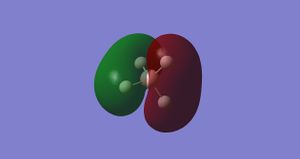
Molecular Orbital 1- This is the non-bonding orbital from the very deep in energy 1s AO from boron. It is so low in energy that there is little/no interaction with the 1s orbitals on the hydrogen.

Molecular Orbital 2- 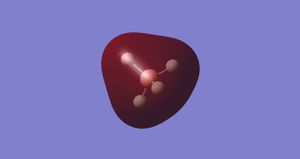This is the bonding orbital from the combination of the 1s orbitals from the hydrogen's and the 2s orbital on the boron.

Molecular Orbital 3,4,5-

These are the degenerate bonding orbitals which arise form the combinations of the filled p orbitals and the 1s orbital on the hydrogen's. The are the highest occupied molecular orbitals and are quite high in energy for bonding orbitals. _{Joseph O'Connell-Danes}