Rep:TSvl915

Introduction

Chemical processes are often described in terms of the properties of their reactants, their products and their transition structures.. Many of these properties can be obtained if the potential energy surface of the chemical system is known. The potential energy of a system depends on 3N-6 coordinates where N is the total number of atoms in the system. Product and reactant structures are located in local minima of the potential energy surface. Local minima are a special type of stationary points in which all coordinates lie at a minimum. Transition states are also a special type of stationary points in which all coordinates lie at a minimum except one which lies at a maximum. This can also be expressed using the two equations below:

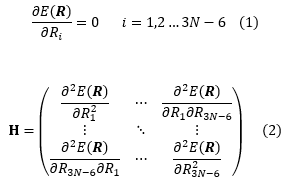
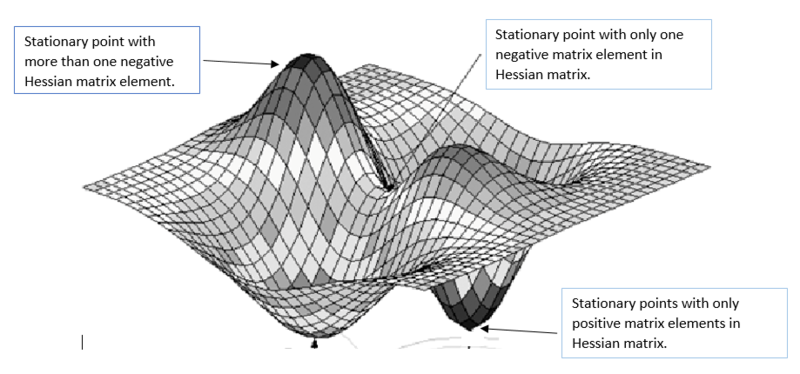
where R refers to a set of coordinates and R_i is the ith coordinate in that set. Every type of stationary point fulfills euqation (1). Local minima have only positive matrix elements in the matrix of second order derivatives H (also called the Hessian matrix, equation 2) whereas transition states have one single negative matrix element. If a stationary point has has more than one negative matrix element it is not a transition structure as this means that it is a maximum in more than one coordinate and that there must be a lower energy pathway between the reactant and product potential energy wells. This reasoning is called the Murrell-Laidler theorem and is illustrated in fig.1 :

Nf710 (talk) 18:30, 7 March 2018 (UTC) This is a good explanation and your figure is excellent. You have clearly read beyond the script. As we discussed in the basis of the degrees of freedom there may be more than 1 negative matrix element. However upon diagonalisation all the off diagonal matrix elements become zero and the diagonal matrix elements become the eigenvalues. In this basis you would be correct. This basis is the normal modes and the axis are the eigen vectors of the diagonalisation.

Fig.1: PES illustrating the Murrell Laidler theorem and showing a transition state as well as a local minimum and a local maximum.

The matrix elements and the vibrational frequencies of structures are related such that correct transition state structures have one negative frequency only whereas correct minimum structures have only positive frequencies if this is not the case the structures are probably wrong.

Based on these concepts specialised software such as Gaussian can be used to model and to explore potential energy surfaces . In this experiment Gaussian was used to investigate three different Diels Alder reactions and a cheleotropic reaction. This included determining their transition state structures, the accurate product and reactant structures, visualising Molecular orbitals (MOs)and nuclear vibrations as well as calculating reaction energies and activation barriers. Furthermore the IRC of the reactions was determined and different bond lengths were tracked throughout the modeled reactions. For this two computational methods were used with Gaussian. The first one was PM6 a semi empirical method based on Hartree Fock theory. This method makes many approximations and some of its more complex terms are obtained from empirical data. It has the advantage being a relatively fast and inexpensive method but its results are unreliable as the empirical reference data may be inadequate and the assumptions made may be too inflexible. The other method is B3LYP/6-31G(d)) which is a density functional theory (DFT) method. These methods aim to deal with the one-electron density rather than the many-electron wavefunction which allows much less demanding computations when solving Schrödinger's equation . B3LYP/6-31G(d))uses a basis set of s and p+d orbitals yet it is not a pure DFT method as Hartree Fock calculations are used to account for exchange correlation. B3LYP/6-31G(d)is is more expensive than PM6 and takes longer but it is also more accurate.

Nf710 (talk) 18:33, 7 March 2018 (UTC) Good understanding of the computational methods your have clear read beyond the script here. Some equations would have backed up your discussion nicely.

Exerciese 1: Diels Alder Reaction between Ethene and Butadiene

Overview

(Fv611 (talk) Very good section, albeit concise. Well done!)

Fig.2: Reaction scheme showing the ethene/butadiene Diels Alder reaction (with a transition state in the middle)

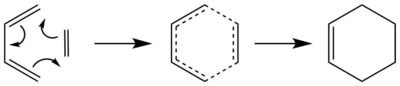
In this exercise the Diels Alder reaction, which is a [4+2] cycloaddition, between butadiene and ethene was investigated (fig.2).

The method used was the following: Butadiene and ethene were optimised separately to a minimum at the PM6 level. To verify that the obtained minimum structures were correct it was made sure that they were converged and that they had no negative vibrations. Subsequently the transition state structure was obtained at the PM6 level using the two otpimised reactant structures. To verify that the transition state structure was correct, it was made sure that it was converged and that it had one negative vibration. An IRC was calculated from the transition state structure at the PM6 level. Finally, the product structure (cyclohexene) was obtained from the IRC and was optimised to a minimum at the PM6 level.

Transition State Analysis

Fig.3: MO diagram of the transition state of the butadiene/ethene Diels Alder reaction

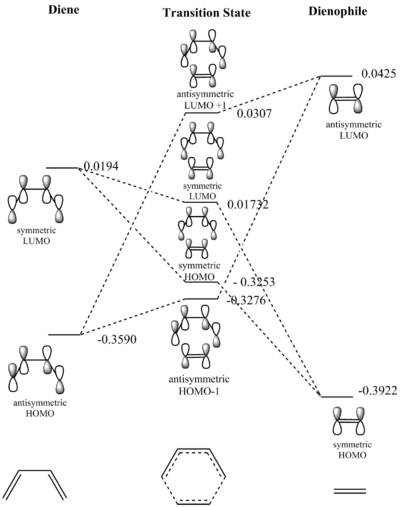
Butadiene HOMO	Butadiene LUMO

Ethene HOMO	Ethene LUMO

TS HOMO-1	TS HOMO	TS LUMO	TS LUMO+1

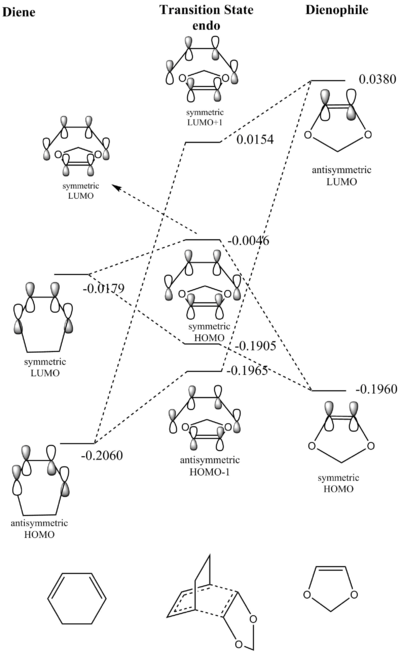
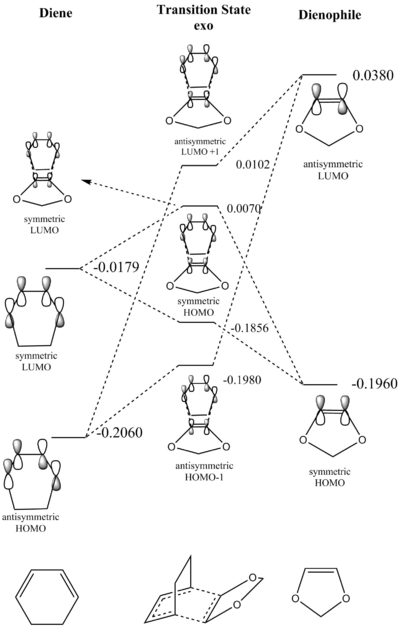
From the transition state MOs shown above and from the transition state MO diagram (fig.3) it can be seen that MOs only interact if they are of the same symmetry (i.e. symmetric MOs interact only with symmetric MOs and not with antisymmetric ones). This implies that for a Diels Alder reaction to be 'allowed' the interacting MOs (i.e. the HOMO and the LUMO of the respective reactants) must be of the same symmetry. Conversely, if the HOMO of one reactant and the LUMO of the other reactant are of opposing symmetry the reaction does not occur.

This can be explained considering the overlap integral of the interacting orbitals. For symmetric-symmetric or antisymmetric-antisymmetric interactions the orbital overlap is non-zero as there are either in-phase or out of phase interactions so that net bonding or net antibonding MOs are generated. Meanwhile, for antisymmetric-symmetric interactions, the overlap integral is zero as the out of phase and in-phase interactions cancel out.

C-C bond length analysis

Fig.4: Animation of the butadiene/ ethene Diels-Alder reaction	Fig.5: C-C bond lengths plotted against the IRC starting from the adduct and progressing to the reactants of the Diels-Alder reaction

Structure	C1-C11/ Å	C1-C4/ Å	C4-C6/ Å	C6-C7/ Å	C7-C14/ Å	C11-C14/ Å
Butadiene	-	1.34	1.47	1.34	-	-
Ethene	-	-	-	-	-	1.34
Trasntion State Struture	2.10	1.38	1.41	1.38	2.10	1.38
Cyclohexene	1.54	1.50	1.34	1.50	1.54	1.54

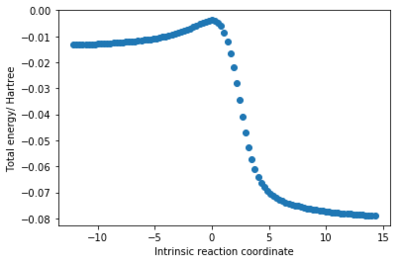
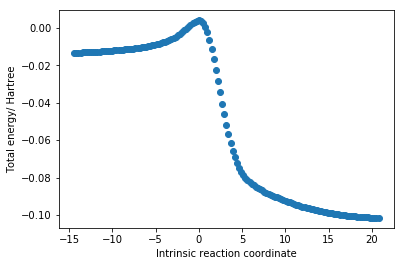
In a Diels-Alder reaction (animated in fig.4), two new C-C sigma bonds are formed (C1-C11, C7-C14), three C=C pi bonds lengthen to become C-C sigma bonds (C11-C14, C1-C4, C6-C7) and one C-C sigma bond (C4-C6) shortens to become a pi bond. This is reflected in fig.5 where all C-C bond lengths are plotted against the intrinsic reaction coordinate (starting from the product and progressing towards the reactants).

In butadiene the C=C bond lengths (C1-C4 and C6-C7, see table) are very close to the standard C=C pi bond length (1.34 Å). Meanwhile, the C-C bond (C4-C6) is shorter than a typical C-C sigma bond (1.54 Å ) which can be attributed to the effects of conjugation.

In the transition state structure the C1-C4 and C6-C7 bond lengths are lengthened compared to the bond lengths in butadiene whereas the C4-C6 bond length is shortened. The C11-C14 bond length is slightly lengthened compared to the bond length in ethene. The C1-C11 and the C7-C14 bond length is 2.1 Å which is less than the sum of two carbon van der Waals radii (3.4 Å ) suggesting that there is some interaction between these carbon atoms.

In the product (cyclohexene) structure the C1-C4 and C6-C7 bond lengths are slightly shorter than the standard C-C bond length (where two sp³ orbitals overlap) which can be attributed to an increased s character in these bonds as they can be seen as an overlap between a sp² and a sp³ orbital.

Transitions State Vibration

Fig.6a: Animation of the complex vibration in the transition state for the ethene/ butadiene Diels Alder reaction	Fig.6b: Animation of the ethene/ butadiene Diels-Alder reaction

Diels-Alder reactions are known to occur via a concerted mechanism. This is underpinned by the negative vibration (animated above in fig.6a) which suggests a synchronous C-C bond formation. Figure 6b shows an animation of the whole reaction.

Files

IRC:File:IRC1vl915.LOG

Exercise 2: Diels Alder reaction between Cyclohexadiene and 1,3-Dioxole

Overview

Fig.7: Overview of the reactions investigated in exercise 2

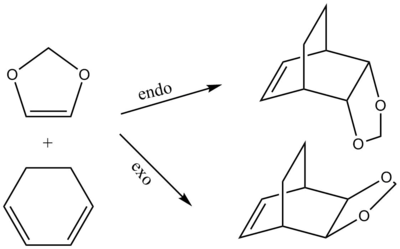
In this exercise the Diels Alder reaction between cyclohexadiene and 1,3 dioxole was investigated (fig.7). In this case two different outcomes are possible, the endo and the exo product.

The method used was the following: The product (either exo or endo) was optimised to a minimum first at the PM6 level then this structure was used to find a minimum structure at the B3LYP/6-31G(d) level. To test whether a correct minimum structure was obtained in each step it was made sure that the structures were converged and that they had only positive vibrations. The optimised product structure was then used to find a transition state structure first at the PM6 level, then the PM6 structure was used to find a transition structure at the B3LYP/6-31G(d) level. To test whether a correct transition state structure was obtained in each step it was made sure that the structures were converged and that they had one negative vibration. An IRC was obtained at the PM6 level from the PM6 transition state. The reactant structures were obtained from the IRC and were optimised to a minimum separately at the B3LYP/6-31G(d) level.

Analysis of the MOS

Fig.8a: This figure shows the MO diagram of the endo transitions state for the inverse electron-demand Dielse-Alder reaction between hexadiene and 1,3 dioxole. Energies are given in hartrees.	Fig.8b: This figure shows the MO diagram of the exo transitions state for the inverse electron-demand Dielse-Alder reaction between hexadiene and 1,3 dioxole. Energies are given in hartrees.

(Fv611 (talk) Good MO diagrams. Could have added a bit more discussion on the differences between endo and exo conformations in term of their relative energies.)

Figure 8 (above) shows the frontier MO diagram for the transition state of the Diels-Alder reaction between cyclohexadiene and 1,3 dioxole for the endo and exo reactions, respectively. The B3Lyp/6-31G(d)-optimised MOs for the nedo and exo transition states are shown below.

The energies obtained from the B3Lyp/6-31G(d) optimisations of the reactants reveal that in this particular reaction the HOMO of the dienophile is higher in energy than the HOMO of the diene. Thus this reaction can be identified as an inverse-electron demand Diels-Alder reaction. An explanation for this is that the dieneophile is more electron-rich than the diene due to the two oxygen atoms in its structure.

Nf710 (talk) 21:43, 7 March 2018 (UTC) This is correct but you have just stated this hypothesis without backing it up with data or a qualitative reason. You should have tabulated the energies from the single point energy calculation.

B3Lyp/6-31G(d) optimised MOs of the transition states

EXO HOMO-1	EXO HOMO	EXO LUMO	EXO LUMO+1

ENDO HOMO-1	ENDO HOMO	ENDO LUMO	ENDO LUMO+1

Reaction energies and Activation barriers at the B3Lyp/6-31G(d) level

	Reaction energy /Ha	Reaction energy/ kJ mol-1	Activation barrier/ Ha	Activation Barrier/ kJ mol-1
EXO	-0.024281	-63.75	0.063858	167.66
ENDO	-0.025668	-67.39	0.060876	159.83

The table above shows the reaction energy and the activation energy for the endo and the exo Diels-Alder reaction. The reaction energy is negative for both reactions which means that they are both thermodynamically favourable. Meanwhile, the endo reaction is more exergonic and has a lower activation barrier and is thus thermodynamically and kinetically favoured over the exo recation. This can be explained considering two factors. Firstly, steric strain, looking at the endo product (fig.7), the (CH₂CH₂)-"bridge" and the 1,3 dioxole are on opposite faces of the cylcohexane ring. For the exo product they are on the same face making it more sterically strained than the endo product. The other factor to consider are secondary orbital interactions. These are bonding interactions which do not lead to a bond but contribute to lowering the energy of transition structures. These secondary orbital inetractions are only present in the endo transition structure (see below) which explains the smaller activation barrier of the endo reaction. Secondary orbital interactions generally explain the endo-selectivity of Diels-Alder reactions even in cases where the endo product is not thermodynamically favoured over the exo product.

Closer comparison of the endo and exo transition states

ENDO TS	ENDO TS (cartoon)	EXO TS	EXO TS (cartoon)

The table above shows the HOMO of the endo and exo transition state structures. In the case of the endo transition structure a stabilising in-phase iteraction can be seen between the p orbitals of the oxygen atoms and the centre-back lobes of the diene. The exo transition structure lacks these stabilising secondary orbital interactions and is thus higher in energy.

Nf710 (talk) 21:46, 7 March 2018 (UTC) Your energies are correct and you have come to the correct conclusions. Your diagrams weere very nice. You could have gone into a few more details about the reaction kenetics and the electron demand of the reaction.

Files

1,3 dioxole:File:OTHER B3LYP.LOG cyclohexadine:File:CYCLOHEXADIENE B3LYP.LOG Products exo:File:B3LYP EXO.LOG Product endo:File:ENDO B3LYP MINIMUM.LOG IRC endo:File:IRC PM6 3.LOG

Exercise 3: Diels-Alder and cheleotropic reactions between o-xylylene and sulphur dioxide

Overview

Fig.9 : This reaction scheme shows the three main reactions between o-xylylene and sulphur dioxide.

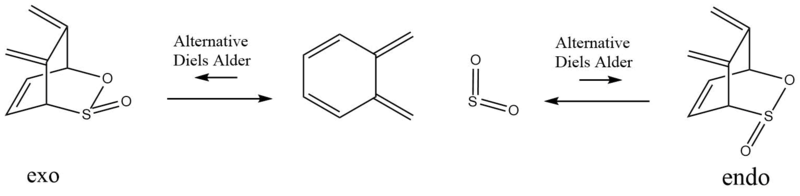
In this exercise the possible reactions between sulphor dioxide and o-xylylene were investigated. One possible reaction path is a Diels Alder reaction wehre, just as in exercise 2, an endo and exo product can be generated (fig.9 ). Another possible reaction path is a cheleotropic reaction (fig.9). Finally, an alternative Diels-Alder where the cyclohexadiene acts as the diene (see fig.10) was considered as well.

The method used was the following: At first the products were optimised to a minimum at the PM6 level. To confirm that the right mininmum structure was obtained it was verified that the structure was converged and that all frequencies were positive. This product structure was then used to obtain the transition state structure at the PM6 level. To confirm that the right transition state structure was obtained it was verified that the structure was converged and that one negative frequency was present. Subsequently an IRC on the PM6 level was taken on the obtained transition state. The reactant structures were obtained from the IRC and optimised individually at the PM6 level. The thermochemical data of these optimised structures was used to calculate the reaction energies and the reaction barriers at the PM6 level.

The three main reaction pathways

Exo Diels-Alder	Endo Diels-Alder	Cheleotropic

The animations above show that during the three reactions the C-C bonds in the six-membered ring of o-xylylene shorten and that in the product structure this six-membered ring contains six C-C-bonds of equal lengths which lie between the typical C-C single and C=C double bond lengths. This is indicative of electron delocalisation and not surprising as fig.9 shows that a six-membered aromatic ring is present in the products of all three reactions. Aromatic systems are very stabilised which explains why the products are thermodynamically favoured over the reactants in all three reactions.

Thermochemistry of the reactions

The table below shows the reaction energies and activation barriers for the three reaction pathways calculated at the PM6 level.

	Reaction energy/ Ha	Reaction energy/ kJ mol-1	Activation barrier/ Ha	Activation energy/ kJ mol-1
ENDO	-0.037049	-97.27	0.031816	83.53
EXO	-0.03729	-97.89	0.033329	87.51
Cheleotropic	-0.058745	-154.23	0.040317	105.85

The table above shows that as expected the activation barrier of the endo reaction is lower than the activation barrier of the exo reaction. This can again be explained by secondary orbital interactions between the p-orbital of the oxygen atom (the one not involved in the ring formation) and the lobes on the diene. In contrast to the reaction investigated in exercise 2 the exo product is less sterically strained than the endo prodcut as the oxgen atom that is not in the ring occupies the equatorial position which is less sterically strained (see fig.9). Thus the exo product is thermodynamically favoured over the endo product. The cheleotrpic product is the most stable but also has the largest activation barrier so, unless under condtions in which the Diels-Alder reacions can be reversed, it is unlikely to be generated.

Analternative Diels Alder reaction

Fig.10: This reaction scheme shows the alternative Diels Alder reaction of o-xylylene and sulphur dioxide.

	Reaction energy/ Ha	Reaction energy/ kJ mol-1	Activation barrier/ Ha	Activation energy/ kJ mol-1
ENDO	0.006865	18.06	0.043326	113.78
EXO	0.008562	22.52	0.046311	121.62

Figure 10 shows that another couple of Diels Alder reactions than the ones mentioned so far is possible between o-xylylene and sulphur dioxide. The table above shows the reaction energies and activation barriers for this aletrnative Diels-Alder reaction calculated at the PM6 level.

The table above shows that these alernative Diels Alder reactions are clearly endergonic and therefore thermodynamically unfavourable. This can be attributed to the lack of an aromatic ring in the product structures which was present in the three reactions discussed above (see fig.9). Furthermore, the activation barriers for these Diels Alder reactions are much higher than for the reactions shown in fig.9 which makes it unlikely that they occur.

Fig.11 below summarizes the thermochemical discussion for exercise 2:

Fig.11 : This scheme summarises the thermochemistry for all discussed reactions between o-xylylene and sulphur dioxide.

(I know this isn't meant to be to scale, but your diagram suggests that the alt products are similar in energy to the cheletropic TS. There are other ways of placing all this data on the same diagram Tam10 (talk) 11:56, 6 March 2018 (UTC))

Files

sulphur dioxide:File:SULPHUR DIOXIDE FROM IRCvl915.LOG o-xylylene:File:DIENE 3 MINIMUMvl915.LOG Products exo:File:MINIMUM productvl915exoex3.LOG Product endo:File:PM6 MINIMUMproduct endovl915.LOG Product cheleotropic:File:PM6 MINIMUMproduct endovl915.LOG alternative exo: File:MINIMUM 1altDAexoproductvl915.LOG alternative endo: File:Alternative Diels Alder endo product minimum PM^vl915.LOG IRC endo:File:IRC PM6 ex3 endovl915.LOG IRC exo:File:IRC ON TSex3vl915exo.LOG IRC cheleotropic:File:IRC PM6 1cheleovl915.LOG alternative DA exo:File:IRC 1altDAexoproductvl915.LOG alternative DA endo:File:IRCalternativdielsalderendo.LOG TS alternative DA: exo:File:TSaltDAexovl915.LOG endo:File:TSvl915alternativdielsalderendo.LOG TS normal DA:exoFile:TS exovl915ex3.LOG endo:File:TS PM6 ex 3 endo.LOG

Ring opening of 2,3 dimethylaziridine

Overview

Fig.12 : This reaction scheme shows the electrociyclic ring opening of 2,3 dimethylaziridine .

The ring opening of 2,3 dimethylaziridine is an example of an electrocyclic reaction. Electrocyclic reactions are concerted processes in which an acyclic conjugated system is converted into a ring system by the formation of a sigma bond between the ends of the conjugated system. The reverse process is also an electrocylic reaction and these reactions are usually reversible in nature.

The method used was the following: The product structure (ring-open) was otpimised to a minimum at the PM6 level. To test if the obtained structure was correct it was verified that it was converged an that it had only positive vibrations. Subsequently a transition state structure was obtained at the PM6 level from the optimised product. To test if the transition state structure was correct it was verified that it was converged an that it had one negative vibration only. An IRC was obtained from the transition structure at the PM6 level. Finally, the reactant structure (ring closed) was obtained from the IRC and otpimised to a minimum at the PM6 level.

The Molecular orbitals

HOMO ring closed	LUMO ring closed

HOMO ring open	LUMO ring open

HOMO-1 TS	HOMO TS	LUMO TS	LUMO+1 TS

(You will need to look at the same number of MOs in the reactants and products as TS MOs Tam10 (talk) 12:14, 6 March 2018 (UTC))

Stereochemistry and its rationalisation

Fig.13 : This is an animation of ring opening of 2,3 dimethylaziridine .

The animation above shows that during the ring closure the groups attached to the terminal carbons of the pi system rotate in the same direction (both clockwise). This mode of motion is called conrotation and it is these modes of motion during the electrocyclic ring closure (the counterpart of conrotation is disrotation) which determine the stereochemistry of the ring-closed product. Whether disrotation or conrotation occurs depends on the system and can be predicted by two equally successful models: Woodward-Hoffman analysis and Mobius-Huckel analysis.

Both analyses require to apply a set of rules which then allow to determine the mode of motion. Both analyses, here the rules have to be applied to a a pi system containing 4 electrons, predict conrotation for this electrocyclic reaction.

Meanwhile, whether conrotation or disrotation occurs can also be deduced, looking at the calculated ring-open HOMO.

Fig.14 : This figure shows the effect of conrotation and dirotation on the thermal HOMO .

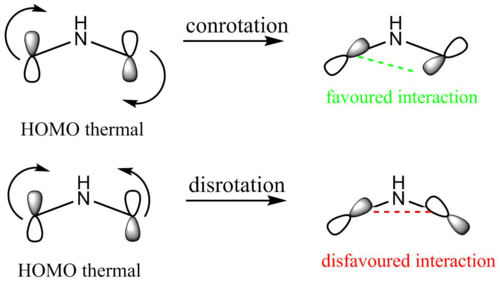
A "cartoon" of the ring-open HOMO (as shown in the Jmols above) is shown in fig. 14. It can be seen that if conrotary motion is applied, lobes of the same phase overlap (a bonding interaction) suggesting that the process is orbital symmetry allowed and that it proceeds through a low-activation energy transition state. If disrotary motion was applied to the the HOMO, lobes of opposite phase would overlap (an antibonding interaction) suggesting that the process is orbital symmetry forbidden and that it proceeds through a high-activation energy transition state. It can thus be assumed that under thermal conditions the reaction occurs with conrotary motion.

It should also be mentioned that if the Woodward Hoffman and Moebius-Hueckel analyses predict conrotation under thermal conditions for a particular system they will predict disrotation for the same system under photochemical conditions. This can also be rationalised for the 2,3 dimethylarizidine system looking at the calculated MOs. Under phtochemical conditions one electron from the HOMO is excited into the LUMO so that the LUMO (under thermal conditions) becomes the HOMO under photochemical conditions.

Fig.15 : This figure shows the effect of conrotation and dirotation on the photochemical HOMO .

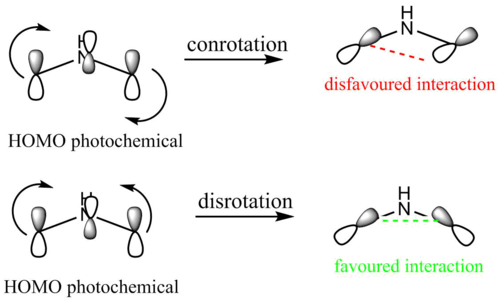
A "cartoon" of the ring-open photochemical HOMO (see "LUMO ring open" in the Jmols above) is shown in fig. 15. If conrotary motion was applied to the the HOMO, lobes of opposite phase would overlap (an antibonding interaction) suggesting that the process is orbital symmetry forbidden and that it proceeds through a high-activation energy transition state. If disrotary motion is applied, lobes of the same phases overlap (a bonding interaction) suggesting that the process is orbital symmetry allowed and that it proceeds through a low-activation energy transition state. It can thus be assumed that under photochemical conditions the reaction occurs with disrotary motion.

Files

Ring closed: File:REACTANT MININMUMperivl915.LOG ringopen:File:RINGOPENFINALVL915.LOG TS:File:TSperivl915.LOG IRC: File:IRCperivl915.LOG

Conclusion

These three exercises show that it is possible to successfully model different Diels-Alder, cheleotropic and electrocyclic reactions with the Gaussian software using semi-empirical and DFT-based methods. Furthermore, the software also makes it possible to visualise molecular orbitals and nuclear vibrations and animations of whole reactions can be generated. The software also allows to obtain thermochemical information of the modeled reactions such as their reaction energies and activation energies. Calculations such as the ones carried out in these experiments have thus the potential to replace expensive and difficult experiments. Further work could be done on more complex cycloadditions as well as other pericyclic reactions such as [3-3] sigmatropic rearrangements for instance. A further next step could be to take into account the surrounding medium (air,solvent...) and surrounding conditions such as temperature and pressure when modelling the reactions.