Rep:TSR:LLL2333

The Cope Rearrangement Tutorial

Objectives:locate the low-energy minima and transition structures on the C6H10 potential energy surface, to determine the preferred reaction mechanism.

Optimizing the Reactants and Products

Optimization to find a local minimum means following the gradient down to dE/dq=0 and d²E/dq²>0

Optimization of Different Conformers Finding Their Local Minimum Energies and the Correspondent Geometries

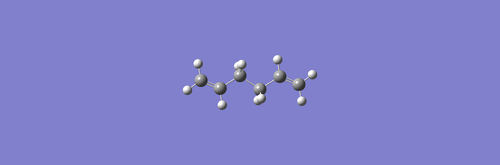
(a)This 1.5-hexadiene molecule was optimized using Hartree Fock with the default basis 3-21G, and the Total Energy obtained is -231.68539585 a.u.

The point group obtained is C2h

. (d)This is anti3

conformer in Appendix 1.

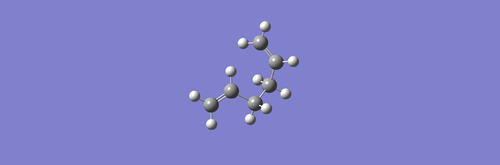
(b) This 1.5-hexadiene has different conformation from the one above. Using the same optimization method, now Total Energy = -231.69266118 a.u. (-0.00726533 a.u. lower than the structure above) and Point group = C1 . (c)Trying to find the conformation with the lowest energy, it turned out that the second structure is the lowest energy possible, (d)which is the same as gauche3

conformer in Appendix 1. This conformation is a compromise between p-orbitals of each ethene sigma-conjugating with the C-H bonds next to it and electronic repulsions (steric hinderance), thus the lowest energy.

Nf710 (talk) 15:46, 19 November 2015 (UTC)Its a mixture of the pi system and the proton you could have shown this by looking at the orbitals in the .chk file. good explanation.

Optimization of the Same Conformer Using Different Theoretical Methods to Compare the Change in its Geometry

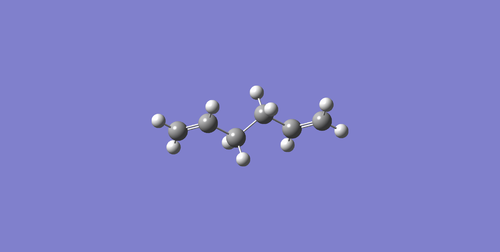
(e)Anti2 1,5-hexadiene is in Ci

symmetry, and optimization at the HF/3-21G
level of theory gives Total Energy = -231.69253528 a.u.

, which is the same compared to -231.69254 a.u. in Appendix 1.

(f) The optimized anti2 conformer was again input for re-optimization at the B3LYP/6-31G*

level, and the result was Total Energy = -234.55970458 a.u.

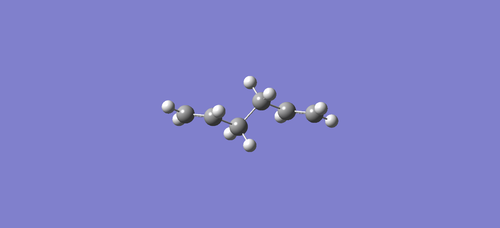
Although the energies calculated are quite different, but there is no meaning to compare the values from different methods (solving Schrodinger Equation with different approximations). The geometry did not change much, as it is still the same conformer. ????B3LYP/6-31G* is closer to the experimental values?show some reference maybe????

Anti2 1,5-hexadiene	optimized at HF/3-21G	optimized at B3LYP/6-31G*
Bond Length(Angstrom) of C¹=C² and C⁵=C⁶	1.31613	1.33824
Bond Length(Angstrom) of C²-C³ and C⁴-C⁵	1.50891	1.50720
Bond Length(Angstrom) of C³-C⁴	1.55275	1.55505
Bond Angle(Degree) of C¹=C²-C³ and C⁴-C⁵=C⁶	124.80575	125.22039
Bond Angle(Degree) of C²-C³-C⁴ and C³-C⁴-C⁵	111.34878	112.64844

Nf710 (talk) 15:49, 19 November 2015 (UTC) You have used the wrong basis set here and hence got the wrong energy I believe. Comparision of geoms is good coudl ahve done the dihedrals though.

Visualize Vibrational Frequencies and Correct the Potential Energies to Compare with Experimental Values

(g)The final energies calculated by Gaussview are the energies of the molecule on the bare potential energy surface, which assumes that the molecule obeys the Third Law of Thermodynamics (The entropy of a perfect crystal at absolute zero is exactly equal to zero.). Nevertheless, the molecule is not perfect crystal in real life, so in order to compare these output values with the experimentally measured quantities, some corrections must be done. These corrections have to be obtained from a frequency calculation.

vibration of 1,5-hexadiene anti2-comformation

The frequencies were all positive and real, indicating the force constants were all positive and this structure was at a minimum on PES as d²E/dq²>0. The calculated IR spectrum looks quite similar to the experimentally measured one (http://webbook.nist.gov/cgi/cbook.cgi?ID=C592427&Type=IR-SPEC&Index=1) and gives useful information such as =C-H stretch around 3000 cm^-1 and C=C stretch around 1500 cm^-1.

Type of Energy	Equation	Explanation	Energy Value (a.u.)
(i) the sum of Electronic and Zero-point Energies	E₀ = E_elec + ZPE	the potential energy at 0 K including the zero-point vibrational energy	-234.416259
(ii) the sum of Electronic and Thermal Energies	E = E₀ + E_vib + E_rot + E_trans	the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature	-234.408965
(iii) the sum of Electronic and Thermal Enthalpies	H = E + RT = E₀ + E_vib + E_rot + E_trans + RT	contains an additional correction for RT which is particularly important when looking at dissociation reactions	-234.408021
(iv) the sum of Electronic and Thermal Free Energies	G = H - TS = E₀ + E_vib + E_rot + E_trans + RT - TS	includes the entropic contribution to the free energy	-234.447881

Nf710 (talk) 15:52, 19 November 2015 (UTC)Good comparison against literature. and nice explanation about the force constants.

Optimizing the "Chair" and "Boat" Transition Structures

Learning Outcomes: three ways to set up a transition structure optimization (i) by computing the force constants at the beginning of the calculation, (ii) using the redundant coordinate editor, and (iii) using QST2. Visualize the reaction coordinate and run the IRC (Intrinisic Reaction Coordinate) and calculate the activation energies for the Cope rearrangement via the "chair" and "boat" transition structures.

(a)Create a Guess Structure for Chair Transition State of Cope Rearrangement

An allyl fragment (CH2CHCH2) was drawn and optimized using the HF/3-21G level of theory so that it was be ready for us to build the transition state with it. Another identical fragment is created by copy and paste, and it was oriented so that the fragments look roughly like the chair transition state (shown in the picture below). However, this could not be done manually, thus a the guess structure was symmetrized by specifying point group = C2h. The distance between the terminal ends of the allyl fragments was set equal or smaller 2.2 Å apart for the reaction to occur.

(b) Optimization of the Guess TS by Computing the Force Constant Matrix (also known as the Hessian) in the First Step which will then be Updated as the Optimization Proceeds

This process is to first calculate d²E/dq² < 0 to see if the initial structure is near the transition state, if so it will continue optimizing following the gradient up until dE/dq = 0 and once again check that force constant is still negative to show it reaches the maximum point.

The guess chair transition state was optimized (Opt+Freq) to a TS (Berny) with the HF/3-21G level of theory calculating the force constants ONCE with the Additional keyword Opt=NoEigen (This stops the calculation crashing if more than one imaginary frequency is detected during the optimization which can often happen if the guess transition structure is not good enough.) and gives a Total Energy = -231.61932181 a.u. and one Imaginary Frequency = -818.00 cm^-1. The negative frequency indicates a negative Force Constant k, d²E/dq² < 0, hence a maximum (transition state) on PES.

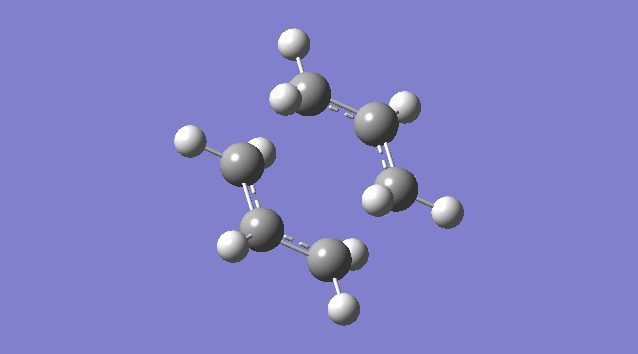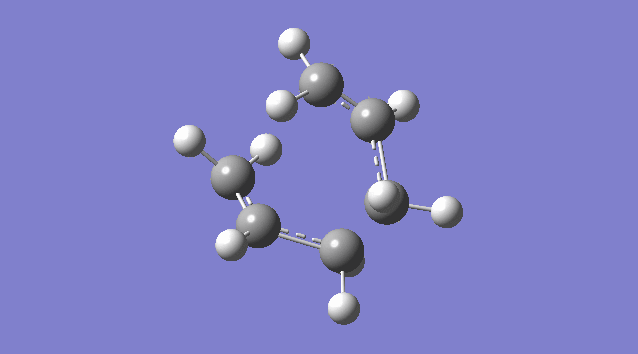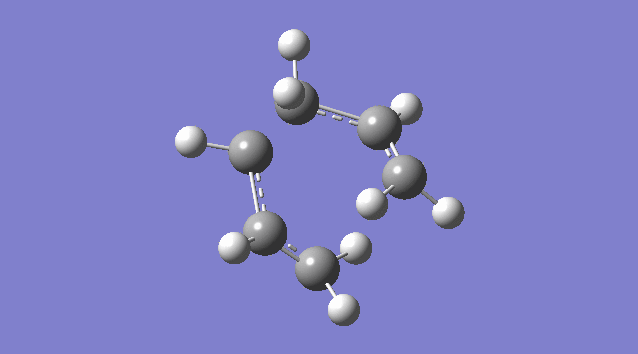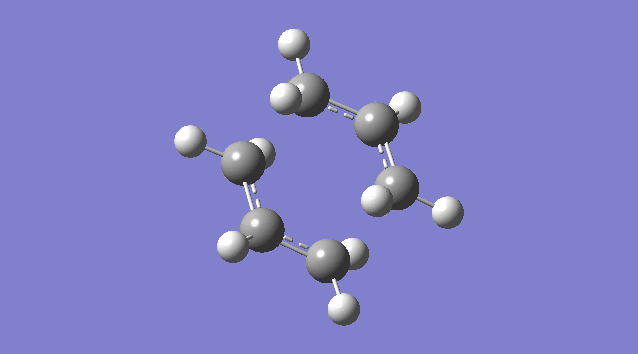
Cope rearrangement vibration of guessing structure of chair transition state

Nf710 (talk) 15:56, 19 November 2015 (UTC) It would have been good here if you could have talked about how the second derivative is the force constant used in the quantum harmonic oscillator and hence is the reason why imaginary frequencies are returned.

(c)(d)optimization of the guess transition state with the frozen reaction coordinates

This process is to make the reaction related coordinates to search the maximum but the rest to search fir minimum.

(e)QST2: Optimization of the Boat Transition State by Providing the Reactant and Relevant Product

This process first needs the set up of a right orientation for the reaction to occur by linking the coordinates of reactant and product, and then it will search for the maximum along the constrained path by interpolation. Once the maximum is found, it will check the imaginary frequency.

The structures of the reactant and the product are both obtained by copy and paste of optimized Ci reactant molecule from (e), with renumbering of their atoms for Cope Rearrangement (as shown below). Tips for numbering atoms: Follow the order of the numbers, start from 1 to2

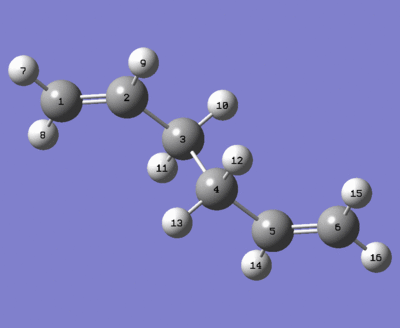
Input of these structures of reactant and product for QST2 results in a failed boat transition state (as shown below).The reason is the QST2 calculation does not consider rotation around the central bond but only translation of the allyl fragments.

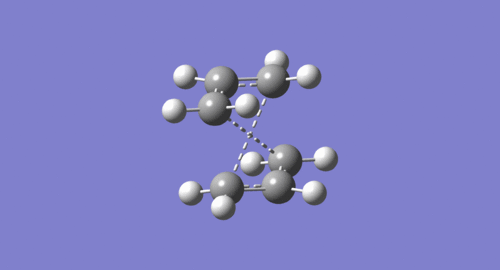
Thus manual rotations should be done before using the QST2 (as shown below).

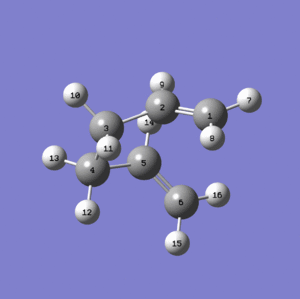
This time a proper boat transition state with Point Group = C2h is obtained.

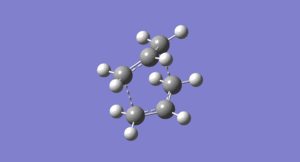
(f)IRC (Intrinisic Reaction Coordinate)

Compared to Appendix 1, the chair transition state is related to the gauche3; the boat transition state is related to the gauche2. To prove this, IRC method can be used to calculate the minimum energy path from a transition structure down to its local minimum on a potential energy surface.

Results for CHAIR transition state are as follows.

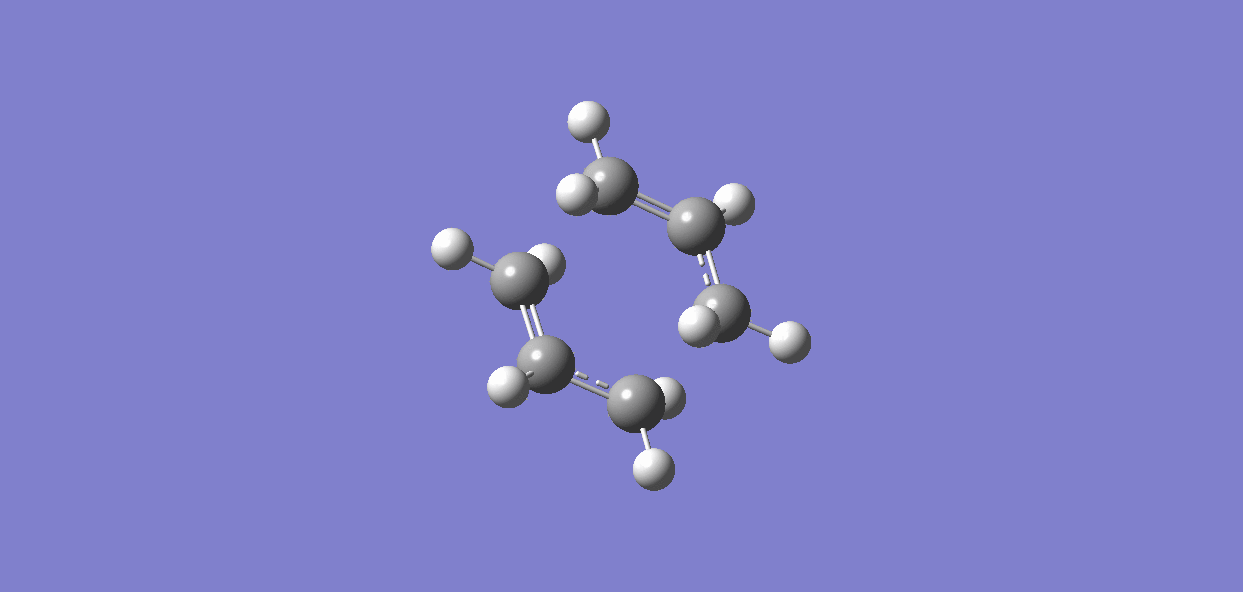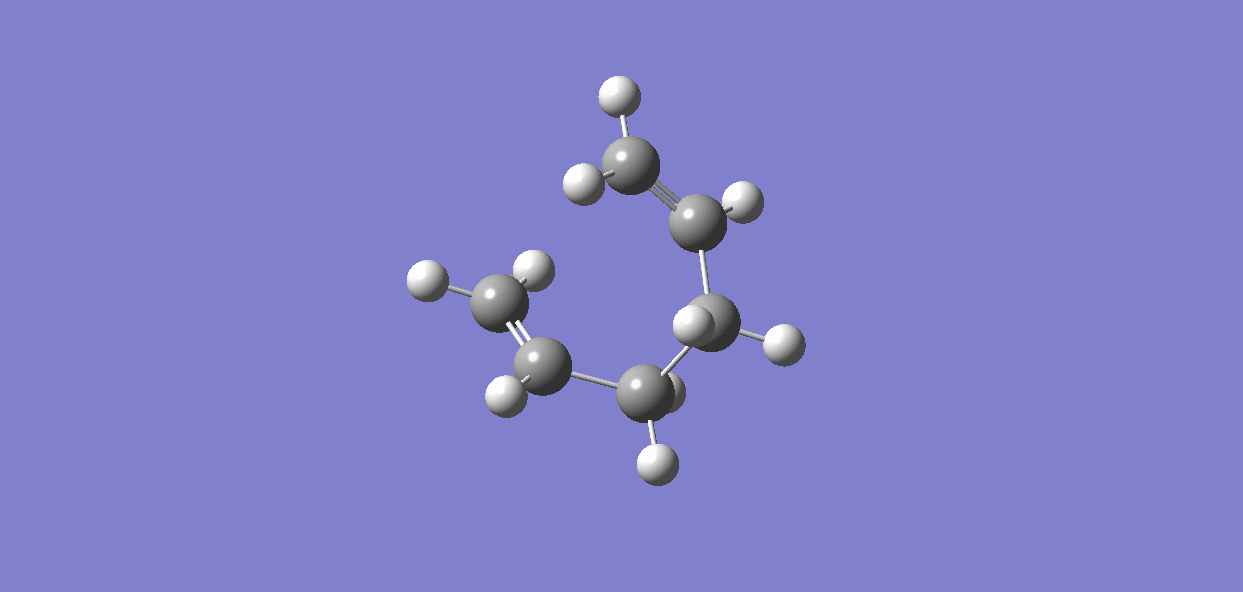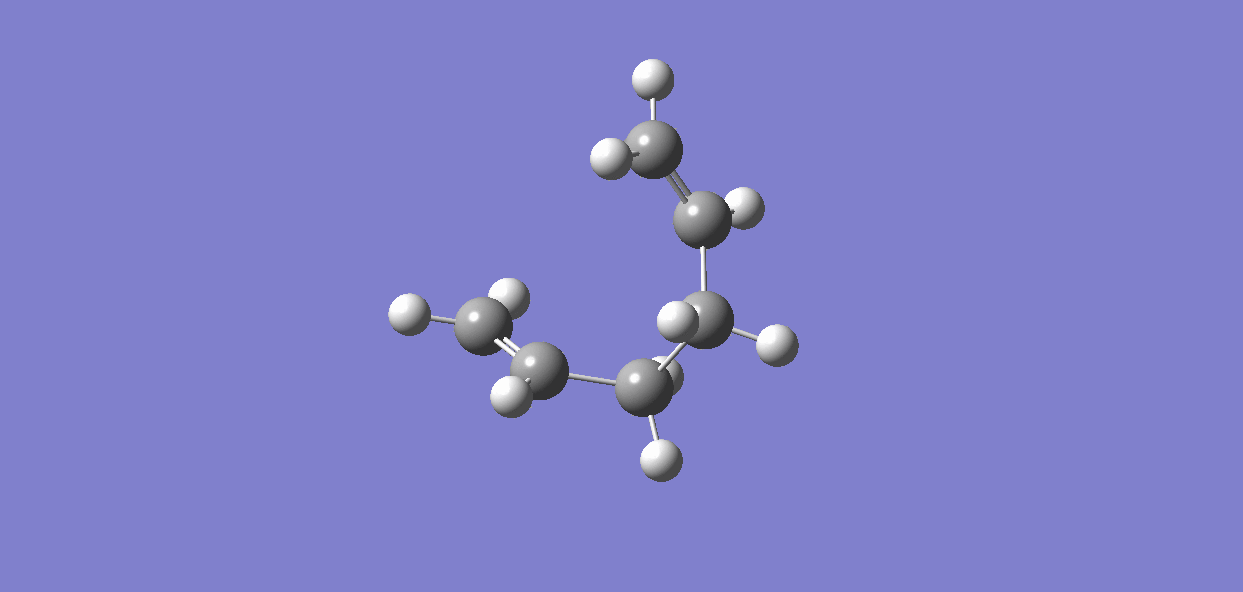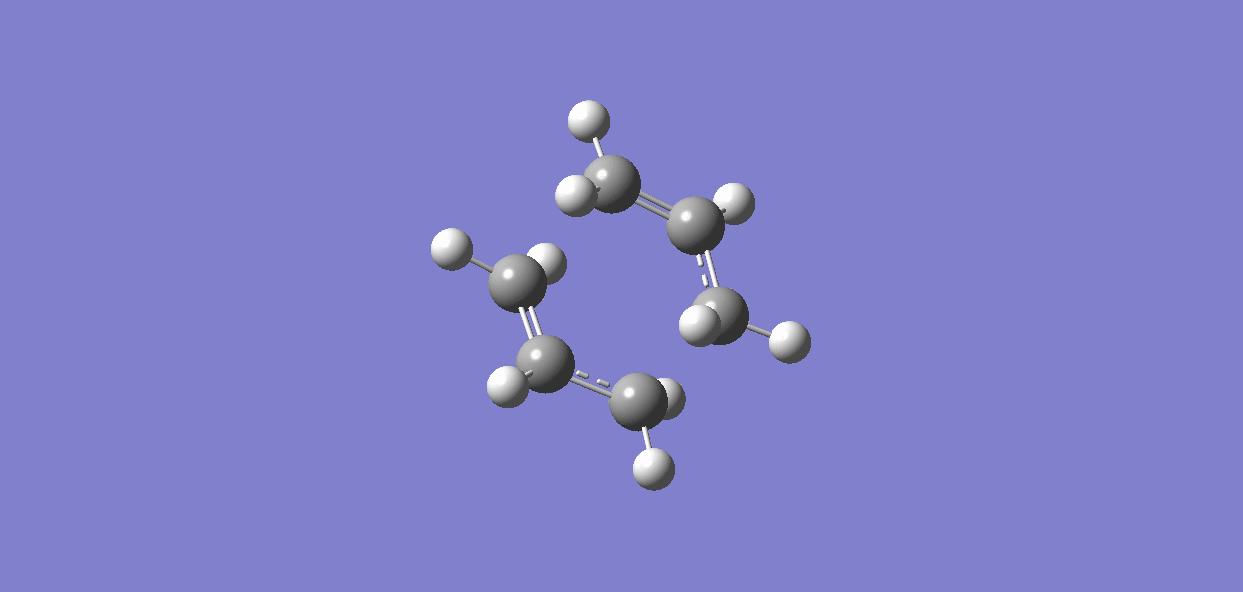
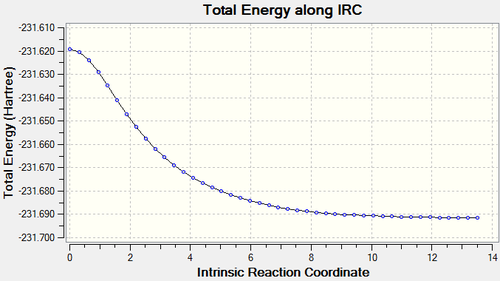
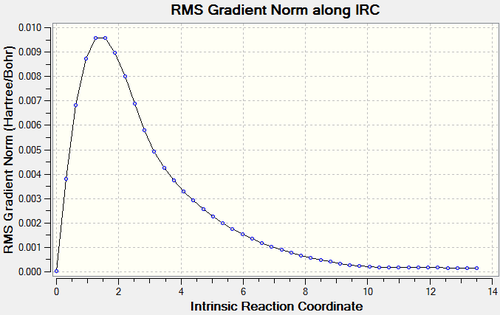
Animation of minimum energy path from CHAIR TS to local minimum of Cope rearrangement

It is clear from the plots that the chair transition state is the maximum energy point (its gradient=0) and energy drops with large gradient when the C-C bond starts forming. The total energy keeps decreasing when the product twisting, but the rate of energy falling gradually declines when the the structure proceeds to the final conformer.

Compared the energies and conformations of IRC results with those data in Appendix 1. It is possible to see the minimum path is a transformation from gauche to gauche2.

Results for BOAT transition state are as follows.

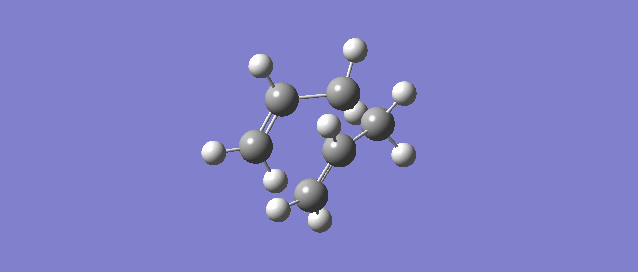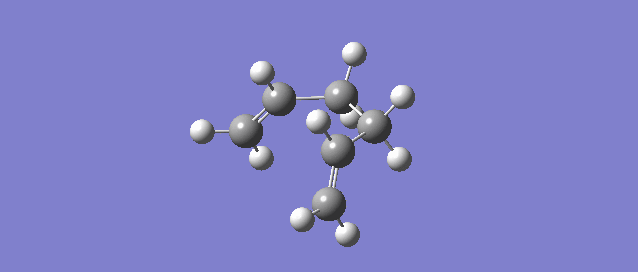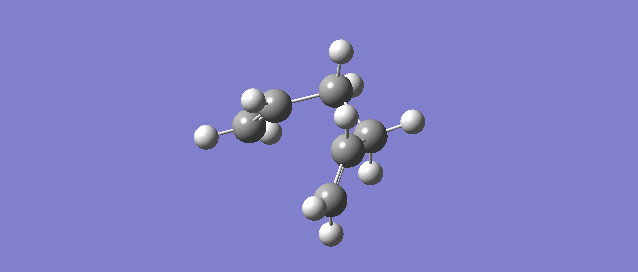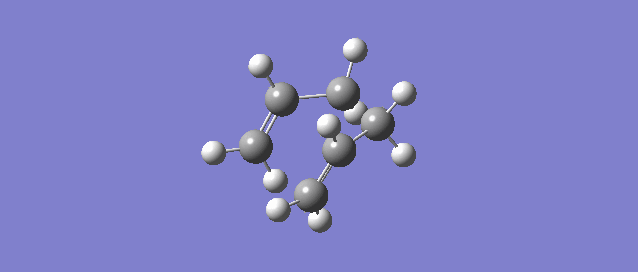
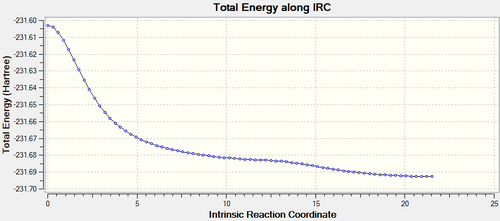
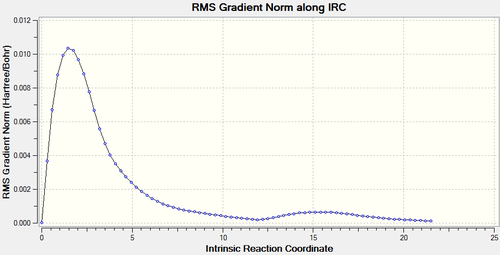
Animation of minimum energy path from BOAT TS to local minimum of Cope rearrangement

It can be seen form the plots that boat transition state is maximum point with gradient=0 and the energy falls as the the C-C is forming. This is corresponding to the minimum path via gauche3 in Appendix 1.

Nf710 (talk) 16:00, 19 November 2015 (UTC) You didn't need to the boat but it is good that you did. You could have determined the structure that it connects by looking at the energy

(g)Calculation of Activation for chair and boat transition states

total energy of chair ts= -234.41636963a.u. total energy of boat ts= -234.49291455a.u.

Nf710 (talk) 16:08, 19 November 2015 (UTC)I can see you have optimised here for the higher basis set. but is this your energy plus zero point energy. either way Its slightly out and i think you have used a slightly different basis set, I will get you 1/2.

Nf710 (talk) 16:08, 19 November 2015 (UTC) Its pretty obvious that you ran out of time here. It was an ok report at first. you seemed to have a good understanding of how the optimisations work. It would have been nice if you could have shown that you knew about the different DFT/HF methods. Its also weird how your energies are slightly out, would be interesting to see what basis set you are using. You seemed to have a good grasp of the theory its a shame you ran out of time.

The Diels Alder Cycloaddition

i)HOMO and LUMO of butadiene

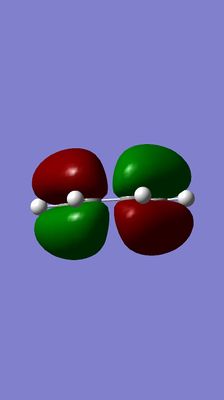
optimized butadiene structure	LUMO	HOMO
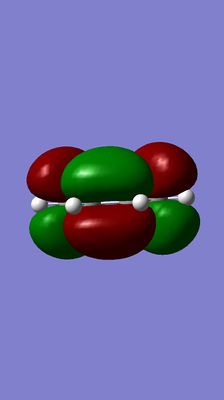optimized butadiene	HOMO of butadiene without a symmetry plane	LUMO of butadiene with a symmetry plane

(Your titles don't correspond to the images and labels. The HOMO is antisymmetric about the plane normal to the carbon atoms, meaning a reflection results in a total phase shift Tam10 (talk) 17:28, 17 November 2015 (UTC))

ii) Computation of the Transition State geometry for the prototype reaction and an examination of the nature of the reaction path.

Diels-Alder TS	Anti-symmetrical LUMO	Symmetrical HOMO
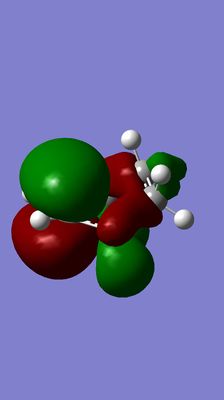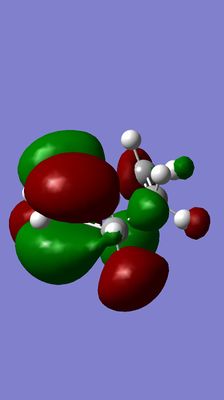Diels-Alder TS	Symmetrical Diels-Alder TS HOMO	Anti-symmetrical Diels-Alder TS LUMO

Diels-Alder TS Vibrations with Imaginary Frequency at -93.39cm-1

(This is the wrong TS. You should expect a synchronous TS with bonds forming between ethene and butadiene. If you're unsure, perform an IRC to check the TS links your reactants and products Tam10 (talk) 17:28, 17 November 2015 (UTC))

The formation is synchronous as shown in the animation. The lowest positive frequency is 224.8cm-1 and the Imaginary Frequency at -93.39cm-1 indicates that the curvature of the TS on the PES is small.

(While it should be synchronous, this particular TS doesn't show a synchronous bond formation Tam10 (talk) 17:28, 17 November 2015 (UTC))

The HOMO of Diels-Alder TS is forming between the LUMO of butadiene and HOMO of alkene because it is apparent from the pictures that these three MOS have the consistent symmetry and the conjugation retains. The allowance of the reaction is due to significant overlap and the consistence of symmetry between the LUMO of butadiene and HOMO of alkene.

(Again, you should expect to see something different if you have the correct TS Tam10 (talk) 17:28, 17 November 2015 (UTC))

bond type	bond length (Angstrom)	comments
the Partly Formed C-C sigma-bond	1.54739	longer than sp3 C-C but shorter than sp2 C=C, in general very close to sp3 C-C
typical sp3 C-C	1.54
typical sp2 C=C	1.47
the van der Waals radius of carbon	1.70	If two carbon atoms get closer than 3.40 Angstrom, they can have van der Waals interactions.

(This is, unfortunately, because the bonds you have marked up are in fact sp3 hybridised Tam10 (talk) 17:28, 17 November 2015 (UTC))

iii) Stereoselectivity of the Diels Alder Reaction

For this section, QST2 method was used for finding transitions states. The first steps was to optimize the structures of hexacyclodiene and the maleic anhydride separately and use them to build up the endo and exo reactants for Diels-Alder reaction.

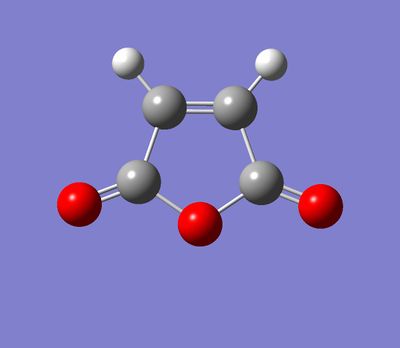
Stereochemistry	Reactants	TS	Product	Comments
Endo	Error creating thumbnail: File with dimensions greater than 12.5 MP Endo Reactants	Endo 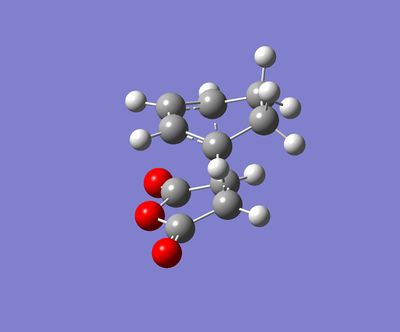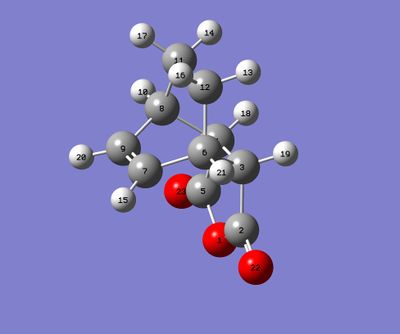TS E(RHF) = -605.61036820 a.u.	Endo product E(RHF) = -605.72132086	The endo TS is stabilized by the secondary orbital overlap effect
Exo	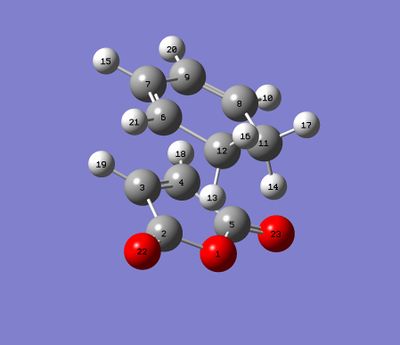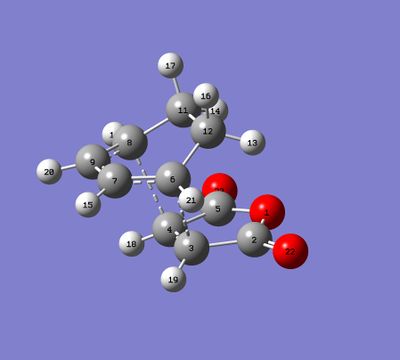Exo Reactants	Exo TS E(RHF) = -605.60359125 a.u.	Exo product E(RHF)= -605.71873535 a.u.	The exo TS is 0.01 a.u. higher than endo TS in energy.

(Best to convert your energy differences into kJ/mol or kcal/mol Tam10 (talk) 17:28, 17 November 2015 (UTC))