Rep:TS:mhardst
Introduction
Molecular Structure via Quantum Mechanics
Molecular structure of various systems can be investigated via quantum mechanical analysis. The Schrödinger equation must be solved, giving the molecular wavefunction of the system (Ψ).[1] The wavefunction of the system can be operated on by the Hamiltonian operator (Ĥ), which is specific for each individual molecular system, and the eigenvalue of the Hamiltonian equation corresponds to the total energy of the molecular system (E).[1] [2]
The Born-Oppenheimer approximation assumes that since nuclei are so much more massive than electrons, electronic motion can take place within a stationary nuclear framework (i.e. nuclei do not have time to respond to electron motion).[1][3] Under the Born-Oppenheimer approximation, we can uncouple nuclear and electronic motion, and treat them separately via quantum mechanics - considering a distinct 'nuclear wavefunction' and 'electronic wavefunction'. [3]
For molecular potential energy surfaces, we are interested only in the electronic wavefunction - which is found to depend on nuclear coordinates, i.e. we can write the electronic wavefunction of the molecule, and hence determine total electronic energy, for a specific nuclear configuration.[3] This is the basis of molecular potential energy surfaces - which are derived by plotting the electronic potential energy value (V) of the overall molecular system, for a particular nuclear geometry (Q) (where Q is a collective variable describing the particular nuclear configuration as a single vector).[2] This is repeated over many possible collective vectors Q, and each potential value at a given Q is plotted.[1][3] This results in the formation of a 'surface' which displays how potential energy varies as a function of nuclear configuration (which itself depends on internuclear separations/bond angles/etc.). [3]
Therefore, to construct a potential energy surface, the electronic Schrödinger equation is solved (for a particular nuclear configuration), and the resultant potential energy value plotted.[3] This is repeated across numerous nuclear configurations. [3] The electronic Schrödinger equation for an n-electron system has the form:[1][3]
Where ri is the vector describing the coordinates of electron i for a given 'fixed' nuclear framework.[1][3]
The electronic Hamiltonian operator has the form:[1][3]
Nf710 (talk) 22:52, 21 February 2018 (UTC) Good understanding of the elementary quantum mechanics behind the PES. You could have gone further to talk about the antisymetry of the electron. and its ramifications on the hamiltonian.
Molecular Potential Energy Surfaces
A molecular potential energy surface contains an abundance of information regarding the molecular reaction dynamics of the given reaction that it describes.
A structure composed of N atoms will have (3N-6) degrees of freedom in its molecular potential energy surface. [2] Potential energy of the structure (V) is a function of these (3N-6) degrees of freedom, and so is embedded in a (3N-5) - dimensional space.[2]
Stationary Points
A stationary point on any potential energy surface is defined as a point which has a first derivative of potential energy V with respect to variable Q equal to zero:[1][2]
However, in order to differentiate between maxima/minima/saddle points, the sign of the second derivative at the point Q must also be taken into account.[1] The set of second derivatives can be formatted into a matrix called the Hessian matrix. [2]
Nf710 (talk) 22:54, 21 February 2018 (UTC) The eiegenvectors of the hessian are a linear combination of the degrees of freedom. These are the vibnrations you see as the degrees of freedom are all moving at once.
Distinguishing Minima and Transition States
Using the Hessian matrix, minima and transition states (saddle points) on a given potential energy surface can be differentiated based on the number of negative Hessian eigenvalues of the matrix.[1]
- A minimum on a potential energy surface is characterized by having no negative Hessian eigenvalues (i.e. all of the Hessian eigenvalues are positive).[1]
- A maximum on a potential energy surface is characterized by having all negative Hessian eigenvalues.[1]
- A transition state is the maximum point on the minimum energy path (MEP) which connects two minima.[2] In the context of the overall potential energy surface, a transition state is a saddle point on the potential energy surface.[4] Saddle points are characterized by having a single negative Hessian eigenvalue. [1]
Frequency Calculations
Physically, a single negative Hessian eigenvalue means that a transition structure can be identified as a molecular geometry with a single imaginary frequency. [2] Therefore, throughout the following investigation, each time a transition structure was located and optimized, a frequency calculation was also performed in order to confirm that the resultant geometry was indeed a true transition structure. A single vibration with a negative frequency (whose vibrational motion corresponds to the (intuitively) expected molecular motion in the transition state) indicated a transition structure had been found.[2]
Analytical Optimization Techniques
For molecular systems of an order greater than diatomic molecules, the quantum mechanics describing the molecular dynamics rapidly becomes extremely complex (as number of degrees of freedom in the wavefunction increases), and fully solving such a wavefunction is beyond the scope of modern-day computational power. [2] Therefore, current molecular geometry optimization techniques must make a series of assumptions in order to be possible within such computational constraints. There are several different models used, two of which were used in the investigation: a semi-empirical approach on the PM6 level, and a DFT (Density Functional Theory) approach at the B3LYP level, on a 6-31G(d) basis set.
Semi-Empirical Technique
For polyatomic systems, the Hamiltonian operator can be incredibly complex, and contain many different terms.[2] This makes determination of the molecular wavefunction extremely difficult, and hence it is hard to find the correct functional form of the potential energy function - which is ultimately desired for molecular reaction dynamics analysis. Therefore, the semi-empirical approach is to use a highly simplified version of the Hamiltonian, as well as including experimentally-derived values as the coefficients within this Hamiltonian.[2]
Density-Functional Theory Method
Density Functional Theory (DFT) presents an alternative route which avoids the molecular wavefunction altogether, but rather determines molecular potential energy indirectly.[2][3] The technique attempts to find the electronic probability density function of the system, and calculates the potential energy value (at each individual geometry) from this.[2] However, this approach is only accurate for calculating the energy values of ground electronic states. [3] It is based on the quantum mechanical outcome that the ground state electronic energy of a given molecular system depends solely on its electronic probability density function. [3]
Comparison
Typically, it is assumed that the DFT approach on the B3LYP level is a more accurate optimization technique than the semi-empirical approach on the PM6 level. However, given the more complex mathematical analysis involved, this computational calculation takes far longer to complete. Therefore, for computational investigations requiring geometry optimization techniques, the decision between which technique is chosen becomes a balance between accuracy and time.
Nf710 (talk) 22:58, 21 February 2018 (UTC) B3LYP is know as a hybrid methdod as it used the DFT hamiltonian to calculate all the terms apart from the exchange correlation which is done with a hartree fock calculation.
Nf710 (talk) 22:58, 21 February 2018 (UTC) This section was really really well done. excellent understanding of the methods and really nicely written.
Exercise 1: Reaction of Butadiene with Ethene
(Fv611 (talk) Very good job across the whole exercise - good, concise discussion throughout. Should have provided a labelled reaction scheme to help with understanding your bond length measurements. Could also have done with explicitly labelling the HOMO and LUMO for your Transition state.)
Molecular Orbital Diagram
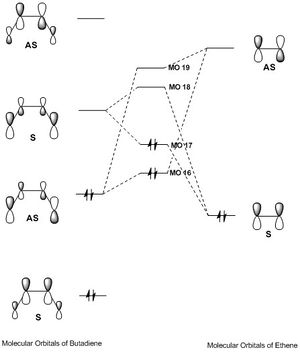
Molecular Orbitals
Ethene
HOMO
This is a symmetric molecular orbital.
LUMO
This is an antisymmetric molecular orbital.
Butadiene
HOMO
This is an antisymmetric molecular orbital.
LUMO
This is a symmetric molecular orbital.
TS
MO 16
This is an antisymmetric molecular orbital.
MO 17
This is a symmetric molecular orbital.
MO 18
This is a symmetric molecular orbital.
MO 19
This is an antisymmetric molecular orbital.
Symmetry Requirements
As can be seen from the above MO diagram:
- The antisymmetric HOMO of butadiene interacts with the antisymmetric LUMO of ethene, producing a bonding/antibonding pair of antisymmetric MOs (MOs 16 and 19).
- The symmetric LUMO of butadiene interacts with the symmetric HOMO of ethene, producing a bonding/antibonding pair of symmetric MOs (MOs 17 and 18).
From this example, it can be concluded that in order for two MOs to interact with one another, they must have the same symmetry, and they will produce a bonding/antibonding pair of MOs which also has this symmetry.[5]
Therefore, this proves that for an 'allowed' reaction, interacting orbitals must have the same symmetry, and there will not be a change of symmetry in the MOs they produce over the course of the reaction.[5]
Orbital Overlap Integral
- Symmetric-symmetric interaction: non-zero orbital overlap integral
- Antisymmetric-antisymmetric interaction: non-zero orbital overlap integral
- Symmetric-antisymmetric interaction: zero orbital overlap integral
C-C Bond Lengths
Butadiene
C(1)=C(2) double bond length: 1.333 A
C(2)-C(3) single bond length: 1.471 A
C(3)=C(4) double bond length: 1.333 A
Ethylene
C(5)=C(6) double bond length: 1.328 A
Transition Structure
C(1)-C(2) bond length: 1.380 A
C(2)-C(3) bond length: 1.411 A
C(3)-C(4) bond length: 1.380 A
C(4)-C(5) bond length: 2.115 A
C(5)-C(6) bond length: 1.382 A
C(6)-C(1) bond length: 2.114 A
Cyclohexene
C(1)-C(2) single bond length: 1.501 A
C(2)=C(3) double bond length: 1.337 A
C(3)-C(4) single bond length: 1.501 A
C(4)-C(5) single bond length: 1.537 A
C(5)-C(6) single bond length: 1.535 A
C(6)-C(1) single bond length: 1.537 A
Change in Bond Length
As the reaction progresses, the two C=C double bond lengths in butadiene increase from 1.333 A to 1.501 A, as they become C-C single bonds in the final product, cyclohexene. Conversely, the intermediate C-C single bond in butadiene shrinks from 1.471 A to 1.337 A as the double bond character emerges from the Diels-Alder reaction.
Meanwhile, the C=C double bond of ethylene increases from 1.328 A to 1.535 A over the course of the reaction, as it adopts a greater single bond character.
As the two components come together to react, the C-C distances between the terminal carbon atoms of both butadiene and ethylene decrease (from infinite separation) to 1.537 A.
Typical Bond Lengths
Typical sp3 C-C Bond Length [6] = (1.525 -1.526) A
Typical sp2 C=C Bond Length [6] = (1.330 - 1.335) A
Van der Waals' Radius of C [7] = 1.70 A
Comparing TS vs. Typical Bond Lengths
In the TS, the double bonds which are weakening/lengthening to become single bonds (the C(1)-C(2) and C(3)-C(4) bonds) have a bond length of 1.380 A - intermediate between typical C-C and C=C bond lengths. The single bond which becomes a double bond during the course of the Diels-Alder reaction (C(2)-C(3)) has a bond length of 1.411 A - also in between typical C-C and C=C bond lengths.
The single bonds which are partially formed between the terminal carbon atoms of the butadiene and ethylene reactant molecules (C(4)-C(5) and C(6)-C(1)) have bond lengths 2.115 A and 2.114 A respectively (which can be assumed as essentially identical, as they are accurate to a high precision of 1 x 10-1 A). This value is significantly larger than the typical C-C bond length of 1.525-1.526 A, indicating that bonding in the TS is far from complete. However, this length is also much less than twice the Van der Waals' radius of Carbon (3.40 A), thus proving that there is actually a significant extent of bonding between the terminal carbon atoms of each reactant molecule in the transition structure.
Transition State Reaction Path Vibration
The vibration which corresponds to the reaction path at the transition state is that which has an imaginary frequency (corresponding to the single negative Hessian eigenvalue).[1][2][4]
The C-C single bonds which form between the terminal carbon atoms of the butadiene and ethylene components form simultaneously, i.e. the C-C bond formation is synchronous.
Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole
In this exercise, the Diels-Alder cycloaddition between cyclohexadiene and 1,3-dioxole was analysed. Both the exo and endo Diels-Alder cycloaddition pathways were examined.
All reactant/product/transition state geometries were optimised to the semi-empirical PM6 level, followed by subsequent reoptimisation of the resultant structure to the DFT B3LYP level, on a 6-31G (d) basis set.
(Fv611 (talk) Your MO diagrams are very nicely done. As you are showing both the endo and the exo conformations, it would have been nice to extend the discussion and include the differences between the two conformations in terms of their relative MO energies.)
MO Diagram for the Exo Transition State
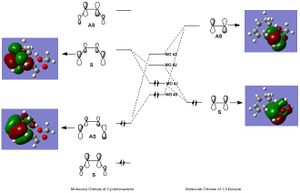
(Given that the frontier molecular orbitals of cyclohexadiene and 1,3-dioxole are analogous in shape to those of butadiene and ethene, respectively, this MO diagram uses the more simple butadiene/ethene MOs as schematic diagrams - simply for clarity).
MO 40
This is an antisymmetric molecular orbital.
MO 41
This is a symmetric molecular orbital.
MO 42
This is a symmetric molecular orbital.
MO 43
This is an antisymmetric molecular orbital.
MO Diagram for the Endo Transition State

(Given that the frontier molecular orbitals of cyclohexadiene and 1,3-dioxole are analogous in shape to those of butadiene and ethene, respectively, this MO diagram uses the more simple butadiene/ethene MOs as schematic diagrams - simply for clarity).
MO 40
This is an antisymmetric molecular orbital.
MO 41
This is a symmetric molecular orbital.
MO 42
This is a symmetric molecular orbital.
MO 43
This is an antisymmetric molecular orbital.
Type of Diels-Alder Reaction
From analysis of the relative energy levels of the froniter molecular orbitals of both cyclohexadiene and 1,3-dioxole, it can be concluded that this particular Diels-Alder reaction is an inverse electron demand cycloaddition.[8]
An inverse electron demand Diels-Alder reaction is defined as having the strongest interaction between the HOMO of the dienophile (1,3-dioxole), and the LUMO of the diene (cyclohexadiene) (i.e. this pair of frontier molecular orbitals are closest in energy, so have the strongest interaction).[8][9]
The inverse electron demand nature of this Diels-Alder reaction can be easily justified by considering the electron-donating nature of the two ring-oxygen atoms in the 1,3-dioxole dienophile. Each oxygen atom donates electron density via an sp3-hybridised lone pair of electrons into the C=C π* antibonding orbital. [8] This interaction raises the energy of the 1,3-dioxole HOMO, by such an amount that it has a greater energy than the HOMO of the diene (cyclohexadiene). Thus, an inverse electron demand Diels-Alder cycloaddition takes place.[8][9]
Nf710 (talk) 23:06, 21 February 2018 (UTC) It would have been nice if you could have plotted this data somewhere. I see you have got the pictures in your MOs diagrams so must have done the calculation.
Kinetic and Thermodynamic Analysis
| Reaction Pathway | Activation Energy/ kJmol-1 | Reaction Energy/ kJmol-1 |
|---|---|---|
| Exo Diels-Alder | +200.1 | -31.27 |
| Endo Diels-Alder | +192.3 | -34.91 |
(All values given to 4 significant figures).
Nf710 (talk) 23:09, 21 February 2018 (UTC) These energies are not correct sadly. I suspect you have calculated your reactants wrong as the energy gap between the endo and exo results is correct. for both activation energy and the reactant energy.
These results allow some conclusions to be drawn about the kinetic and thermodynamic nature of the [4+2]-cycloaddition.
- The endo pathway has a lower activation energy than the exo pathway, and therefore, by the Arrhenius equation (k=Ae(-Ea/RT) where Ea represents activation energy), the endo pathway has a larger rate constant (k), so occurs more rapidly. Hence, the endo product is formed more rapidly and so is dubbed the 'kinetic product'.[8]
- The endo pathway has a more negative reaction energy than the exo pathway, and so given that both reaction pathways begin at the same energy level (same reactants), the endo adduct must inherently be more thermodynamically stable, i.e. it is the 'thermodynamic product'.[8]
Therefore, the endo adduct is both kinetically and thermodynamically favoured, so completely dominates the product distribution of the Diels-Alder reaction between cyclohexadiene and 1,3-dioxole - regardless of whether the reaction takes place under kinetic (low temperature/short reaction times) or thermodynamic (high temperature/long reaction times) conditions.[8]
Nf710 (talk) 23:08, 21 February 2018 (UTC) Excellent discussion of kinetics using the arrhenius equation.
Secondary Orbital Interactions
The 'Endo Rule' applies to all Diels-Alder reactions. It describes how the endo product dominates the product distribution (when the reaction is under kinetic control), despite often being the less thermodynamically stable product.[8] The endo adduct is always kinetically favoured because it has a lower energy transition state than the corresponding exo adduct. [8]
The reason for the greater stability of the endo transition state lies in considering secondary orbital interactions in the HOMO.[5] These are additional interactions which are not formally involved in bond formation between the diene and dienophile components.[5] These secondary orbital interactions are the in-phase overlap of other p-orbitals in the dienophile (other than those involved in the C=C π-bond) with the newly forming intermediate C=C π-bond at the back of the diene component, in the transition state. [8][5]
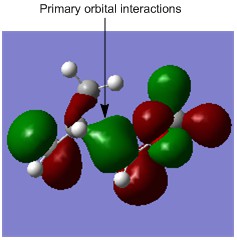
HOMO of the Exo Transition State
In the transition state for the exo pathway, there are no secondary orbital interactions, so there is no additional stabilising factor affecting the energy of the exo transition state. [8][5]
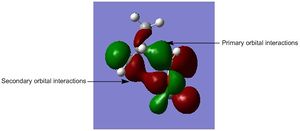
HOMO of the Endo Transition State
There are significant secondary orbital interactions in the transition state of the endo pathway. [5] These interactions are in-phase, so will provide additional stability to the transition state.[8][5] This makes the transition state for the endo pathway more stable than that of the exo pathway, and hence, this explains why the endo pathway has a lower activation energy than the exo pathway.[8] [5] This is the origin of the 'Endo Rule' in Diels-Alder reactions.[8][5]
Nf710 (talk) 23:11, 21 February 2018 (UTC) This was a really good section. Your discussion was really good. But sadly your energies were incorrect. You were still luckily able to get the correct conclusions from them however, so I have awarded you there marks there.
Exercise 3: Diels-Alder vs. Cheletropic
In this exercise, three possible reaction pathways between a molecule of o-xylylene and sulfur dioxide were analysed. Both the exo and endo Diels-Alder cycloaddition pathways between the external cis-butadiene fragment of o-xylylene and sulfur dioxide were examined, as well as an alternative pericyclic reaction called a cheletropic reaction.
All reactant/product/transition state geometries were optimised only to the semi-empirical PM6 level.
Diels-Alder Reaction
Exo

Endo

Cheletropic

Bonding in the Ring
During the course of each of the three reaction pathways studied, the internal cis-diene component (within the ring) conjugates with the newly-forming C=C double bond. This results in delocalisation of the π-character of the orbitals over the entire 6-membered ring, forming an aromatic (planar; 6π-electron) 6-membered ring component in the transition state.[8] (The overall transition state itself is also aromatic, since it has 10π-electrons, i.e. obeys Hückel's (4n + 2) π-electron rule for aromaticity). [8] The C-C single bonds in the 6-membered ring all decrease in length over the course of the reaction, as they adopt a greater double bond character. [8] Eventually, this results in the formation a formal benzene ring component in all three products.
Kinetic and Thermodynamic Analysis
| Reaction Pathway | Activation Energy/ kJmol-1 | Reaction Energy/ kJmol-1 |
|---|---|---|
| Exo Diels-Alder | +85.73 | -99.70 |
| Endo Diels-Alder | +81.74 | -99.05 |
| Cheletropic | +104.1 | -156.0 |
(All values given to 4 significant figures).
Comparison of these values allows conclusions can be drawn about the nature of each different reaction:
- The endo Diels-Alder cycloaddition has a smaller activation energy than the exo Diels-Alder pathway. Therefore, using the Arrhenius equation ((k=Ae(-Ea/RT) where Ea represents activation energy), it is readily observed that the endo pathway will have a larger value of k (rate constant).[8] Therefore, ceterus paribus, the endo pathway will take place more rapidly, and the endo product will be formed fastest. The endo product is therefore the 'kinetic product' of the Diels-Alder reaction.[8]
- The exo Diels-Alder cycloaddition has a more negative reaction energy, so is a more favourable pathway. Therefore, given that the exo and endo products both have identical starting materials, a more negative reaction energy means that the exo adduct is the more thermodynamically stable product. Therefore, the exo product is the 'thermodynamic product' of the Diels Alder pathway.[8]
- The cheletropic pathway has a much larger activation energy than both Diels-Alder pathways, so will take place much more slowly. However, the product is also much more thermodynamically stable than either of the exo/endo Diels-Alder adducts. Therefore, for a reaction under kinetic control (low temperature, short reaction times), the cheletropic pathway is unlikely to be observed, but under thermodynamic conditions (high temperature, long reaction times, i.e. equilibration conditions), the cheletropic product would dominate the product distribution.[8]
(One thing that hasn't been considered here is the Diels-Alder products can equilibrate via another TS - where the oxygen moves between the axial and equatorial positions. This is much lower in energy than the other TSs Tam10 (talk) 10:50, 26 February 2018 (UTC))
All of this information can be clearly summarised in a schematic reaction profile, showing relative energy levels of the reactants, transition states structures, and products of each of the exo/endo Diels-Alder and cheletropic cycloadditions:
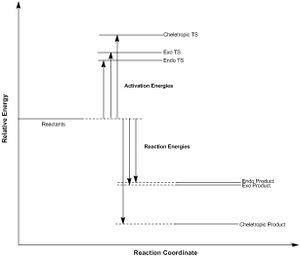
(Well written section. The images at the start could be bundled into a table to make more efficient use of space. The values of the barriers and reaction energies should be included in the reaction profile diagram Tam10 (talk) 10:50, 26 February 2018 (UTC))
Conclusion
In conclusion, the optimised transition states for the cycloaddition reactions of butadiene/ethene, cyclohexadiene/1,3-dioxole and o-xylylene/sulfur dioxide were all studied. Quantum mechanics provided a sound theoretical proof for the definitive location of a transition state - a transition state corresponds to a saddle point on the potential energy surface for a given reaction, and hence has a single negative Hessian eigenvalue. [1][2] [4] This corresponds to a geometry with a single vibration with a negative frequency. [2] [4]
In particular, the frontier molecular orbitals for the Diels-Alder reactions between butadiene and ethene, and a substituted butadiene derivative (cyclohexadiene) and an ethene derivative (1,3-dioxole) were analysed, and the symmetry of the interacting orbitals, and the molecular orbitals they produce in the transition state, were predicted. These predictions were subsequently matched to the computationally-derived molecular orbitals for each of the optimised transition states. These studies allowed conclusions to be drawn about the orbital symmetry requirements of such reactions - only orbitals of matching symmetry can interact.[5] Also, the electronic nature of the observed Diels-Alder reactions was deduced, from comparison of the relative energy levels of the HOMO/LUMO (the frontier orbitals) of the reacting components. From this analysis, the Diels-Alder reaction between cyclohexadiene and 1,3-dioxole was found to be an inverse electron demand Diels-Alder cycloaddition. [8][9]
Furthermore, these optimisation studies also allowed relative energy values of the reactants, products and transition states of each of the different reactions to be calculated. Hence, for each of the relevant reactions studied, the activation energies and reaction energies could be calculated, which in turn allowed deduction of the kinetically and thermodynamically favoured products for each type of reaction.[8]
Appendix
Exercise 1
IRC:
https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:MHARDSTEX1_TS_METHOD3IRC_ATTEMPT1.LOG
Products:
https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:MHARDSTEX1_TS_CYCLOHEXENE_PM6OPTT_ATTEMPT1.LOG
Exercise 2
B3LYP Optimised Cyclohexadiene:
https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:MHARDST_CYCLOHEXADIENE_B3LYPOPT_ATTEMPT1.LOG
B3LYP Optimised 1,3-Dioxole:
https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:MHARDST_EX2_13DIOXOLE_B3LYPOPT_ATTEMPT1.LOG
B3LYP Optimised Exo Product:
https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:MHARDST_EX2_EXOPRODUCT_B3LYP_ATTEMPT1.LOG
B3LYP Optimised Endo Product:
https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:MHARDST_EX2_ENDOPRODUCT_B3LYPOPT_ATTEMPT1.LOG
IRC Exo Pathway:
https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:MHARDST_EX2_EXOTS_OPTIMISEDTS_IRC_ATTEMPT2.LOG
IRC Endo Pathway:
https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:MHARDST_EX2_ENDOTS_TSOPTIMISED_IRC_ATTEMPT2.LOG
Single Point Energy Calculation for the Exo Pathway:
https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:MHARDST_EXOSINGLEPOINTENERGY_ATTEMPT1.LOG
Single Point Energy Calculation for the Endo Pathway:
https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:MHARDST_ENDOSINGLEPOINTENERGY_ATTEMPT1.LOG
Exercise 3
PM6 Optimised o-Xylylene:
https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:MHARST_EX3_XYLYLENEREACTANT_PM6OPT_ATTEMPT4.LOG
PM6 Optimised Sulfur Dioxide:
References
</references>[1] </references>
[4] </references>
[3] </references>
[6] </references>
[7] </references>
[8] </references>
[9] </references>
[5] </references>
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 1.14 1.15 P. Atkins and R. Friedman, Molecular Quantum Mechanics, Oxford University Press Inc., New York, 2011
- ↑ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 2.11 2.12 2.13 2.14 2.15 2.16 2.17 I. N. Levine, Quantum Chemistry, Prentice-Hall Inc., New Jersey, 2000
- ↑ 3.00 3.01 3.02 3.03 3.04 3.05 3.06 3.07 3.08 3.09 3.10 3.11 3.12 3.13 A. Hinchliffe, Modelling Molecular Structures, John Wiley & Sons, Chichester, 1996,
- ↑ 4.0 4.1 4.2 4.3 4.4 S. J. Moss and C. J. Coady, "Potential-Energy Surfaces and Transition-State Theory", J. Chem. Educ, 1983, 60 (6), pg. 455 - 461
- ↑ 5.00 5.01 5.02 5.03 5.04 5.05 5.06 5.07 5.08 5.09 5.10 5.11 I. Fleming, Frontier Orbitals and Organic Chemical Reactions, John Wiley & Sons, London, 1976
- ↑ 6.0 6.1 6.2 D.R.Lide Jr., "A Survey of Carbon-Carbon Bond Lengths", Tetrahedron, 1962, 17 (3 - 4), pg. 125 - 134
- ↑ 7.0 7.1 M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, "Consistent van der Waals Radii for the Whole Main Group", Journal of Physical Chemistry A, 2009, 113 (19), pg. 5806 - 5812
- ↑ 8.00 8.01 8.02 8.03 8.04 8.05 8.06 8.07 8.08 8.09 8.10 8.11 8.12 8.13 8.14 8.15 8.16 8.17 8.18 8.19 8.20 8.21 8.22 8.23 J. Clayden, N. Greeves, S. Warren and P. Wothers, Organic Chemistry, Oxford University Press Inc., New York, 2012
- ↑ 9.0 9.1 9.2 9.3 R. Bruckner, Advanced Organic Chemistry, Academic Press, San Diego, 2002
