Rep:TS:Rwz15
Introduction
Potential Energy Surfaces
On a potential energy surface(PES) there can be many different points of interest especially for more complex molecules where there can be multiple minima which corresponds to all the different stable configurations of the molecule, these minima might derive from the same transition state or from different ones depending on how closely related they are. The lowest energy minima is known as the global miniam and corresponds to the thermodynamic product of a reaction. In this lab we are trying to locate these minima and the transition states corresponding to them.
A minima is a point on the PES where any deviation from that point will lead to an increase in energy. The transition state however is a point at which energy will only decrease in one direction while movement in any other direction will cause an increase in energy. The path at which energy decreases is known as the reaction pathway and can be visualised by running an IRC of the transition state. Mathematically the PES shows the energy of the reaction system with respect to the location of the molecules. By calculating the first derivative we can identify both minima and transition states but it does not tell us any more information. We require the second differential which correspond to the force constant. A minima will have only positive force constants corresponding to the increase in energy in all directions while transition states will have one negative force constant corresponding to the reaction pathway.
TNf710 (talk) 23:31, 29 November 2017 (UTC) The PES has 3N-6 Dimensions. these are the degrees of freedom.
Calculation Methods
There are three method by which you can use to calculate and locate a transition state using Gaussian. The methods increases in difficulty and length but requires less knowledge of the transition state. Method 1 is very unreliable if you have no prior knowledge of the transition state as it requires guessing the transition state and then optimising it to a minimum. Without prior knowledge, being just slightly off could lead to obtaining a structure that is either not the desired minima or just the completely wrong. Method 2 involves drawing a guess transition state followed by optimising to an minimum after freezing the bonds that would be involved in the reaction, this gives a structure that can be optimised to transition state quite reliably. This method still requires some knowledge of the transition state. Method 3 however can be used to obtain the transition state without any knowledge of it, it involves first optimising the products or reactants to a minimum. The structure obtained is then modified to reflect how the reaction would proceed to the transition state, the bonds involved are once again frozen and the structure minimised, the resulting structure can then be optimised to an minimum. The only caveat to this method is that it doesn't work with transition states that have a geometry far from that of the minima.
Computational Methods
In this lab we will mainly be using two types of computational methods, being PM6 and B3LYP. PM6 is a semi-empirical method which uses pre-calculated integrals from experimental data to solve the Hamiltonian making is much faster and less expensive as fewer integrals need to be evaluated. The downside to this method is that the results can be inaccurate as there are many approximations that have been applied making it not a true reflection of what is actually happening. The B3LYP method is a hybrid function based on Hartree Fock and Density Functional Theory (DFT), this method uses the Hartree Fock method of calculating the exchange integrals so is more expensive to run as it involves the calculation of all the integrals in the matrix of the Hamiltonian. B3LYP however gives very accurate results even though it only uses 3 parameters to do its calculations. [1]
Nf710 (talk) 23:34, 29 November 2017 (UTC) This is a pretty good attempt at explaining the computational models used. B3LYP uses DFT to calculate all the terms of the hamilltonian apart from the exchange correlation term which is calculated used a HF calculation.
Exercise 1: Reaction of Butadiene with Ethene
(Fv611 (talk) Great job! The whole exercise has everything that we ask and the MO diagram was especially thought through.)
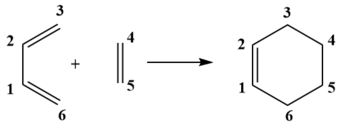
Molecular Orbitals
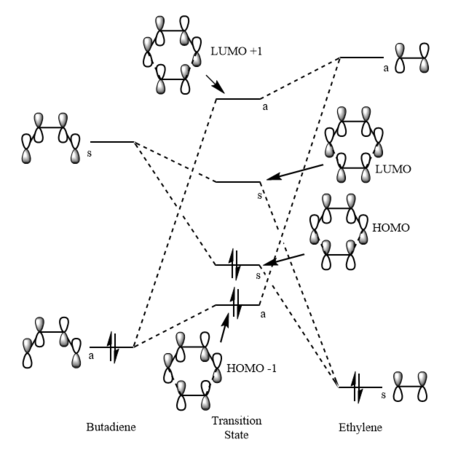
Looking at the molecular orbitals of both the reactants and the transition state allows us to determine the interacting orbitals of the transition state. We can see from Table 1 below that both the HOMO and the LUMO of the transition state are formed from the HOMO of the ethene and the LUMO of the Butadiene, which are both symmetric. The HOMO of the Butadiene and the LUMO of the ethene, which are both antisymmetric also interact to give the HOMO-1 and the LUMO+1 of the transition state. As a result we can conclude that only orbitals of the same symmetry can interact to give new molecular orbitals, reactions are therefore only allowed when orbitals of the same symmetry can interact and so orbitals of opposite symmetry cannot interact and hence the reaction will be disallowed. The orbital overlap integral of symmetric-antisymmetric interaction is zero as they do not mix while both symmetric-symmetric and antisymmetric-antisymmetric interactions have a non-zero orbital overlap integral.
The molecular orbitals of the transition state are higher in energy than both the HOMOs of the reactants due to the reaction barrier that needs to be reached in order for a reaction to take place. The HOMO-1 of the Transition state has a greater contribution from the HOMO of Butadiene, while LUMO+1 has a greater contribution from the ethene showing that the LUMO of ethene is higher in energy than the HOMO of butadiene. The HOMO of the transition state has a larger contribution from the ethene HOMO and the LUMO of the transition state has a larger contribution from the LUMO of Butadiene. As the HOMO of the Butadiene and the LUMO of the Ethene are closest in energy, this is an example of an normal electron demand Diels-Alder reaction.
| HOMO of Ethene | LUMO of Ethene | HOMO of Butadiene | LUMO of Butadiene | ||||||||
| HOMO - 1 of TS | HOMO of TS | LUMO of TS | LUMO + 1 of TS |
Carbon-Carbon bond lengths
| Bonds | Butadiene and Ethene | Transition State | Cyclohexene |
|---|---|---|---|
| C1-C2 | 1.4708 | 1.4111 | 1.3370 |
| C2-C3 | 1.3334 | 1.3798 | 1.5008 |
| C3-C4 | - | 2.1148 | 1.5372 |
| C4-C5 | 1.3273 | 1.3818 | 1.5346 |
| C5-C6 | - | 2.1147 | 1.5371 |
| C6-C1 | 1.3334 | 1.3798 | 1.5008 |
As the reaction proceeds, the single bond on Butadiene (C1-C2) shortens due to the carbons changing from sp3 hybridised to sp2 hybridised while the opposite is true for the ethene double bond (C4-C5) which lengthens as the hybridisation changes from sp2 to sp3. Both the double bonds on Butadiene also lengthen as their sp2 character is lost. The 2 bonds that form have a bond length that is within two times the van der waal radius of carbon of 1.7Å showing that the two molecules are starting to interacting during the transition state and once the bond forms they shorten to that of a single C-C bond.[2] Typical C=C double bond lengths for ethene are normally around 1.3305Å and C-C single bonds lengths are 1.54Å.[3] These lengths match up to the cyclohexene product with bonds adjacent to the double bond being slightly shorter due to the pulling effects of the electron density.
Transition State
The vibration shown above corresponds to the negative vibration of the transition state due to the negative force constant when calculating the frequency of vibrations. The formation of the 2 bonds is synchronous as the vibration shows that both ends of ethene and butadiene move together at the same time. Further proof is seen in the IRC where both bond are formed in the same frame.
log file of optimised cyclohexene TS
log file of optimised cyclohexene product
Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole
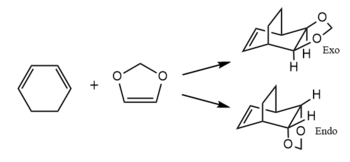
Molecular Orbitals

Analysis of the Molecular Orbitals of the reactants and the transition states shows that this reaction is an inverse electron demand Diels-Alder reaction as the orbitals of the reactants which are closest in energy and hence interacts the most strongly are the HOMO of the Dioxole and the LUMO of the cyclohexadiene. This is possible because the oxygens on Dioxle can donate electron density into the double bond raising the energy of both the HOMO and LUMO of Dioxole compared to a normal ethene molecule. This causes the HOMO of the Dioxole to be closer in energy with the LUMO of the cyclohexadiene.
The large energy gap between the HOMO of cyclohexadiene and the LUMO of dioxole means that they only interact weakly, as a result in the transition state the HOMO -1 is only destabilised slightly and so the energy of the HOMO -1 does not move above the energies of the reactants. Like the reaction in exercise 1, this reaction can only occur if orbitals of the same symmetry interact, this is shown in table 3 below.
Nf710 (talk) 20:57, 30 November 2017 (UTC) If you want to compare reactants quanitatively you should run a single Point energy on the reactants geom. The you can a actually sede what the enegies of the orbitals are in the same PES
| HOMO-1 of Endo TS | HOMO of Endo TS | LUMO of Endo TS | LUMO+1 of Endo TS | ||||||||
| HOMO-1 of Exo TS | HOMO of Exo TS | LUMO of Exo TS | LUMO+1 of Exo TS |
Thermochemistry

The thermochemistry data from the calculations enabled us to calculate the reaction barriers and energies which are shown in table 4 below. From the data we can see the endo transition state requires less energy to achieve than the exo, this is due to the secondary orbital overlap between the p orbitals of the oxygens and the pi system orbitals of the diene stabilising the transition state, showing that the endo product is the kinetic product. When considering the reaction energies, the endo product is also the thermodynamically more stable product and this can also be attributed to the secondary orbital overlap which still can be seen in the product. Another reason could be due to sterics, in the exo product the bridgehead could interact unfavourably with the carbon between the two oxygens which does not occur in the endo product. As a result, the data shows that the endo product is both the kinetically and thermodynamically more favourable product. The secondarry orbital overlap can be seen in figure 5 shown right.
| Product | Reaction Barrier KJmol-1 | Reaction Energy KJmol-1 |
|---|---|---|
| Endo | 158.47 | -68.75 |
| Exo | 166.30 | -65.15 |
log file of optimised cyclohexadiene
log file of optimised endo product
log file of optimised exo product
Nf710 (talk) 21:33, 30 November 2017 (UTC) Good second section. This is nice and concise. Your energies are correct and you have come to the correct conclusions.
Exercise 3: Reaction of o-Xylylene with SO2
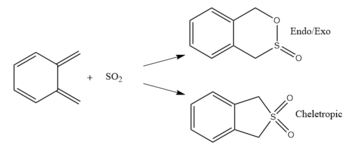
IRCs
The files below show the IRC of the three possible products formed by reaction of o-xylylene and sulphur dioxide, the reactions are mainly driven by the aromatisation of the stable ring. In both the exo and endo products the bonding of sulphur dioxide is asynchronous, as the oxygen bonds before the sulphur whereas the cheletropic product has synchronous bonding of both ends of the o-xylylene to sulphur. By definition a cheletropic reaction is a cycloaddition where the two bond are formed on a single atom.
 |
 |
 |
Thermochemistry
After calculating the reaction energies and barriers of the 3 possible products formed, it can be concluded that the kinetic product is the endo product due to it having the lowest reaction barrier for reaction making it the most accessible under non equilibrating conditions, this is due to interaction between the non bonding oxygen and the diene of xylylene stabilising the transition state. The thermodynamic product is the cheletropic product as shown by its lowest reaction energy, this is due to the presence of larger bond energies as a S=O bond and a S-C bond has a greater bond energy than the combined energy of both a single C-O and S-O.[4]. The cheletropic product has the highest transition state due to the formation of a highly strained 5 membered ring compared to a strain free 6 membered ring. Under mild conditions where equilibration could occur the exo products is expected as the cheletropic porduct has a much higher activation energy so will form less often.
Xylylene is highly reactive and unstable due to it wanting to form an aromatic ring structure to stabilise itself. This can be seen in the IRC where the aromatic ring forms before the bonds to SO2 forms.

(Avoid using curves for reaction diagrams. Straight lines are easier to use and read Tam10 (talk) 12:19, 24 November 2017 (UTC))
| Product | Reaction Barrier KJmol-1 | Reaction Energy KJmol-1 |
|---|---|---|
| Endo | 81.73 | -99.05 |
| Exo | 85.72 | -99.70 |
| Cheletropic | 104.45 | -156.03 |
log file of optimised cheletropic TS
log file of optimised sulphur dioxide
log file of optimised xylylene
log file of optimised endo product
log file of optimised exo product
log file of optimised cheletropic product
Alternative Diels-Alder Pathway
 |
 |
o-xylylene can undergo another Diels-Alder reaction at an alternative site which is shown above. The thermochemistry data for these reactions shows that energy would have to be put in for reaction to occur, this is shown by a positive reaction energy. The reaction barriers are also much higher compared to the corresponding products at the normal site, this is because reaction at this site prevents the formation of the stable aromatic ring prior to bond formation.
| Product | Reaction Barrier KJmol-1 | Reaction Energy KJmol-1 |
|---|---|---|
| ENDO | 111.95 | 16.22 |
| EXO | 119.79 | 20.68 |
log file of optimised endo TS at alternative site
log file of optimised exo TS at alternative site
log file of optimised endo product at alternative site
log file of optimised exo product at alternative site
Conclusion
To conclude, the use of PM6 or B3LYP have provided to be extremely useful in predicting the outcomes of Diels-Alder type reactions. For more accurate results B3LYP should be used but PM6 calculations will allow for quick results which can be used to get a rough idea of the chemistry of the reaction. In exercise 1 we looked at a normal electron demand Diels-Alder reaction and looked at which orbitals interacted to form the transition state, further analysis of C-C bond lengths matched that of literature showing the reliability of computational methods. In exercise 2 we proceeded to look at an inverse electron demand Diels-Alder reaction and tabulating the thermochemistry data we can conclude that the endo product is both the kinetic and thermodynamic product. In exercise 3 we looked at a Cheletropic reaction and showed that it was more thermodynamically stable even though it has a much larger activation energy due to a strained 5 membered transition state. Further calculations revealed a less favourable site of reaction on xylylene which would require an input of energy in order to react.
References
- ↑ Miehlich, Burkhard, et al. "Results obtained with the correlation energy density functionals of Becke and Lee, Yang and Parr." Chemical Physics Letters 157.3 (1989): 200-206.
- ↑ Bondi, A_. "van der Waals volumes and radii." The Journal of physical chemistry 68.3 (1964): 441-451.
- ↑ Craig, Norman C., Peter Groner, and Donald C. McKean. "Equilibrium structures for butadiene and ethylene: compelling evidence for π-electron delocalization in butadiene." The Journal of Physical Chemistry A 110.23 (2006): 7461-7469.
- ↑ Cottrell, T. L. "The Strength of Chemical Bonds, 2nd edit." (1958)
