Rep:TS(wl5015)

Introduction

For a simple 1D potential energy surface, the transition state is the maximum point which has zero first derivative and negative second derivative. For a complex system, the potential energy surface shows many local maxima and minima, so it is difficult to tell which pathway is the reactive pathway, and hence locates the transition state.

In these exercises, the mechanisms of three pericyclic reactions were investigated using Gaussian; the transition states were analysed further using IRC. Locating the transition state was very important for a reaction pathway, and three methods were introduced; each of them had advantages and disadvantages. Method 1 was the fasted, but required a close approximation to the transition state. Method 2 also required a good approximation of the transition state; atoms involved in the reaction were freezing, and the rest of the system was optimized to minimum. Method 3 was the most reliable one, and it was based on method 1 and method 2. It started at the product, broke the bonds which formed in the forward reaction, and followed method 1 and method 2, so more additional steps are needed for this method.

Along the reaction coordinate, the transition state was found when the first derivative of potential energy surface equalled to zero. For the optimization, we used semi-empirical method PM6 first to generate a suitable structure and reoptimised using DFT method B3LYP/6-31G(d). From frequency calculation, we obtained vibration modes, which could be used to confirm if the transition state was correct. In frequency calculation for the transition state, the frequency of the first mode is negative, which corresponds to the negative force constant of stretching of the breaking/forming bond. IRC files generated was also used to confirm the correct transition states.

In each cycloaddition reaction, two new sigma bond formed concerted. Cycloaddition reaction was regio-selective; the way which the dienophile approached determined the region outcomes, endo-product or exo-product.

Nf710 (talk) 21:03, 21 February 2018 (UTC) You havent swrritten about how to find a TS on the PES or talk about the quantum chemical methods

Exercise 1: Reaction of Butadiene with Ethylene

Fig. 1 Reaction of Butadiene with Ethylene

The first reaction was a [4+2] cycloaddition between butadiene and ethylene. There were no additional substituents on both of the molecules, so there was no regioselective problem. For more complex Diels-Alder reaction, the presence of substituents on different positions showed very good selectivity to one of the product. to Both reactants and product were optimised at PM6 level. Method 3 was use to generate the correct transition state. The two sigma bond formed in the reaction were deleted, separated to 2.2 Å, and frozen. Further frequency calculation and IRC were run to confirm the TS structure.

TS Frequency calculation and IRC

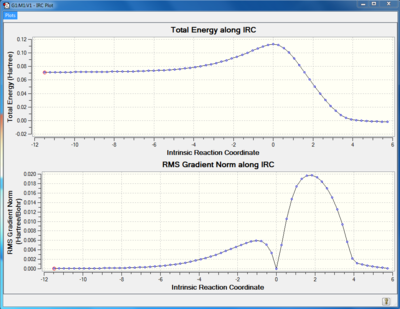Fig. 2 Transition state frequency calculation	Fig. 3 Transition state IRC

MO analysis

(Fv611 (talk) Your MO diagram is nice, but you are not giving the correct explanation for the relative energies of the TS MOs to be higher than expected: this is not due to mixing but due to the fact that this is a TS MO diagram. The TS is the highest energy point on the MEP so it is expected for its orbitals to be higher in energy too. You do not mention the orbital overlap and it's relation to the symmetry requirements. Additionally, you have not shown all 4 relevant TS MOs, and the ones you show are not correct: you have correctly identified that the HOMO should be symmetric, so why show an asymmetric one? I suspect the TS MOs you have shown in the table are not those of the optimised transition state structure.)

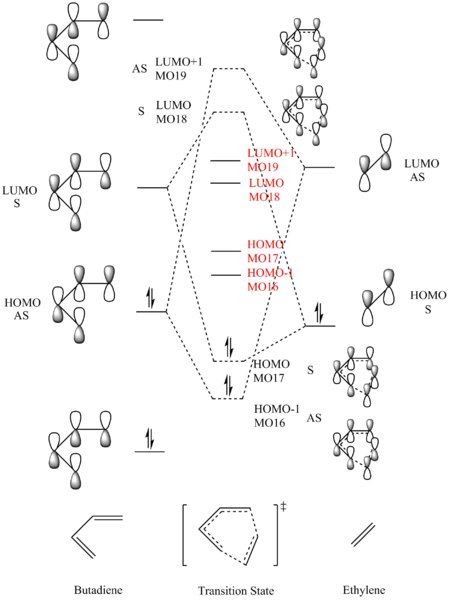
Fig. 4 MO diagram for the formation of the butadiene/ethene TS

S-AS interaction zero

S-S interaction non-zero

AS-AS interaction non-zero

For a reaction to proceed, the orbital symmetries of the two components must be same. AS interacts with AS; S interacts with S. The symmetry of a molecular orbital is determined using symmetry labels C2 and sigma plane. If the MO has C2 rotational axis, it is antisymmetric; if it has a sigma plane, it is symmetric. From that knowledge, we can draw dotted line between interacting orbitals. Antisymmetric HOMO of butadiene interacts with antisymmetric LUMO of ethylene; symmetric LUMO of butadiene interacts with symmetric HOMO of ethylene. This way of interaction gives best overlap. The interaction of HOMO of diene and LUMO of dienophile gives better overlap, because the energy difference between them is smaller.

The energy difference between HOMO and LUMO in related to the conjugation of the molecule. Butadiene has 4 sets of p orbitals which electrons can delocalise around compared to two fixed p orbitals in ethylene. The more conjugated the system, the smaller the energy gap between them.

According to the calculation of the energy of HOMO, HOMO-1, LUMO and LUMO+1, the energy of bonding MOs are higher than the expected value, and the energy of antibonding MOs are lower than the expected value. This is because the presence of MO mixing. MOs of same symmetry will mix to some extent, and result a slightly change in sequence of MOs.

Table 1. MOs of reactants, transition states and products

Butadiene

Ethylene

Transition state

Product

HOMO

LUMO

Bond length analysis

Table 2. Typical C-C / C=C bond lengths
sp3-sp3 C-C	sp3-sp2 C-C	sp2-sp2 C-C	sp2-sp2 C=C	The Van der Waals radius of the C atom
1.54 Å	1.50 Å	1.47 Å	1.34 Å	1.7 Å

Table 3. C-C / C=C bond lengths
Butadiene	Ethylene	Transition state	Product
Fig. 5 Butadiene	Fig. 6 Ethylene	Fig. 7 Transition state	Fig. 8 Product
C1=C2 1.333 Å C2-C3 1.471 Å C3=C4 1.333 Å	C1=C2 1.33 Å	C1-C2 1.383 Å C2-C3 2.272 Å C3-C4 1.386 Å C4-C5 2.272 Å C5-C6 1.383 Å C6=C1 1.407 Å	C6-C1 1.337 Å C1-C2 1.501 Å C2-C3 1.537 Å C3-C4 1.535 Å C4-C5 1.537 Å C5-C6 1.501 Å

For the reactants, butadiene and ethylene, their bond lengths are the same as standard value, C-C 1.47 Å and C=C 1.33 Å. From the reactant to transition state, the C=C bond in ethylene is partially breaking, which was illustrated from the bond length 1.33 Å to 1.38 Å (C3-C4 in TS), which is in between C-C (1.54 Å) and C=C (1.34 Å). Also, C-C bond in butadiene shorted from 1.47 Å to 1.41 Å(C6-C1 in TS). In the transition state, although from the graph there was no bond forming between terminal carbons, the distance between them was 2.27 Å , which is shorter than 2*van der waals’ radius (3.4 Å). This information showed bond forming reaction was taking place. The distance was then decreased to 1.54 Å, which corresponds to sp3-sp3 C-C, which was the new bond forming in the product.

Vibration

From the transition state gif, it shows the formation of two new bonds in cycloaddition reaction is synchronous. (click to show the vibration)

Calculation for exercise 1

PM6 optimized Butadiene: File:EXERCISE-1-LWY-BUTADIENE.LOG

PM6 optimized Ethene: File:ETHENE-OPT-LWY.LOG

PM6 optimized product: File:PRODUCT-NEW-OPT-LWY.LOG

PM6 optimized transition state: File:PRODUCT-NEW-TS1-LWY.LOG

IRC: File:PRODUCT-IRC-LWY.LOG

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Fig. 10 Reaction of Cyclohexadiene and 1,3-Dioxole

Exercise 2 is another example of cycloaddition reaction. The additional complexity of the two reactants give rise to two possible products. For each on them, transition state analysis was carried out, and the kinetic barrier was calculated.

Both products were drawn and analysed using method 3. The product structures were drawn and optimised using PM6, followed by the analysis of transition state using PM6 and B3LYP/6-31G(d).

MO analysis

(Fv611 (talk) Good MO diagrams)

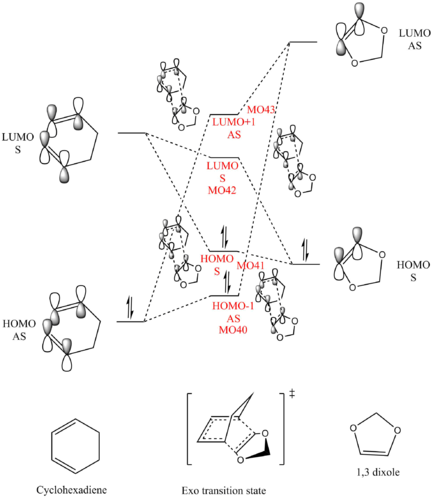
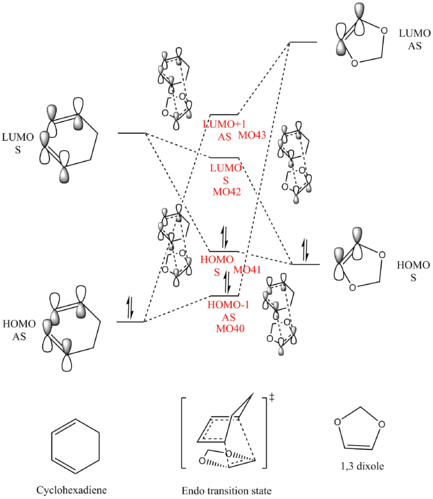
Fig. 11 MO diagram for the Exo Diels-Alder reaction

Fig. 12 MO diagram for the Endo Diels-Alder reaction

There are two types of Diels-Alder reaction, normal electron demand and inverse electron demand. Normal demand Diels-Alder reaction involves an electron rich diene and an electron deficient dienophile; inverse demand Diels-Alder reaction involves an electron deficient diene and an electron rich dienophile.

In this case, the present of oxygen atom next to the dienophile donates electrons into the double bond raising its energy. This selection rule is also shown in the MO diagram. MOs that are close in energy overlap better. Molecules used frontier orbitals to interact, and from the data, we obtained the energy for each orbital.

Therefore, in this case, compare the energy difference between two pairs of HOMO and LUMO, the LUMO of cyclohexadiene and HOMO of 1,3-dioxole have smaller energy difference, thus interacts better.

This result is further proven by single point energy calculation.

Table 4. Energies of HOMO and LUMO
	HOMO energy / a.u.	LUMO energy / a.u.
Cyclohexadiene	-0.20555	-0.01710
1,3-dioxole	-0.19592	0.03797

The energy difference between LUMO of cyclohexadiene and HOMO of 1,3-dioxole: 0.17882 a.u.

The energy difference between LUMO of 1,3-dioxole and HOMO of cyclohexadiene: 0.24352 a.u.

The energy difference between LUMO of cyclohexadiene and HOMO of 1,3-dioxole is smaller, which verify the prediction.

Overall, this reaction was inverse electron demand

Nf710 (talk) 21:06, 21 February 2018 (UTC) If you did this well done. but you could have shown the orbitals or given the file.

Table 5. MOs of Endo and Exo transition states

HOMO-1

HOMO

LUMO

LUMO+1

Endo transition state

Exo transition state

Frequency calculations

Table 6. Optimized structures and vibrational frequencies
	Optimized molecule structure	Vibrational frequency
Cyclohexadiene	Fig. 13 Cyclohexadiene	Fig. 14 Cyclohexadiene vibrations
1,3-Dioxole	Fig. 15 1,3-Dioxole	Fig. 16 1,3-Dioxole vibrations
Exo transition state	Fig. 17 Exo TS	Fig. 18 Exo TS vibrations
Exo product	Fig. 19 Exo product	Fig. 20 Exo product vibrations
Endo transition state	Fig. 21 Endo TS	Fig. 22 Endo TS vibrations
Endo product	Fig. 23 Endo product	Fig. 24 Endo product vibrations

Reaction Energy

Table 7. Gibbs free energy at B3LYP (6-31G(d))
Molecule	Gibbs free energy at B3LYP (6-31G(d)) / hartree	Gibbs free energy at B3LYP (6-31G(d)) / kJmol-1
Cyclohexadiene	-233.324375	-612593.193227
1,3-Dioxole	-267.068647	-701188.7861122
Exo TS	-500.329168	-1313614.33065
Endo TS	-500.332149	-1313622.15727
Exo product	-500.417320	-1313845.77374
Endo product	-500.418692	-1313849.37593

Table 8. Activation energy and Reaction energy
	Activation Energy / kJmol-1	Reaction Energy / kJmol-1
Exo	167.64869	-63.79440386
Endo	159.822074	-67.3965901

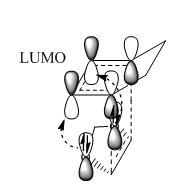
Fig. 25 Secondary orbital interaction in Endo TS

From the Gibbs free energy table, the activation energy is the energy difference between the transition state and reactants; the reaction energy is the energy difference between reactants and the product. The kinetic barrier of endo Diels –Alder reaction is lower, which indicated the endo product is the kinetic product. Also, the reaction energy is more negative, which represented a more stable product. Thus, the endo product was both kinetic and thermodynamic product.

The figure above showed Endo transition state with secondary orbital interaction. The oxygen p orbital and LUMO of cyclohexadiene had same symmetry to overlap, so lone pairs on oxygen delocalised into the LUMO. This delocalisation of electrons stabilised the transition state, which lowered its energy.

In the Exo product, the carbon bridge and 1,3-dioxole ring were in the top phase. The steric clash between these two groups lead to a more unstable structure, which had higher energy.

Calculation for exercise 2

B3LYP optimized dioxole: File:13DIOXOLE-OPT2-LWY.LOG

B3LYP optimized cyclohexadiene: File:CYCLO-OPT2-LWY.LOG

B3LYP optimized endo transition state: File:Exercise2-ENDO-NEW-TS2-LWY.LOG

B3LYP optimized exo transition state: File:Exercise2-EXO-TS2-LWY.LOG

B3LYP optimized endo product: File:Exercise2-ENDO-NEW-OPT2-LWY.LOG

B3LYP optimized exo product: File:Exercise2-EXO-OPT2-LWY.LOG

Nf710 (talk) This was a good section. You have got the correct results and you have come to the correct conclusions which are nicely complemented by diagrams. Your discussion is quite brief and there are a few more points where you could have gone into more detail.

Exercise 3: Diels-Alder vs Cheletropic

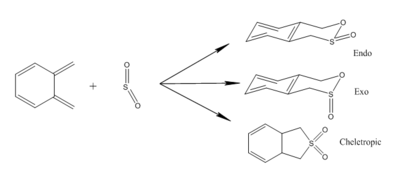
Exercise 3 shows a reaction between xylene and sulphur dioxide. There were two possible routes. One is hetero-Diels-Alder reaction between xylyene (diene) and sulphur dioxide (dienophile), the other is Cheletropic reaction. The hetero-Diels-Alder reaction generates two possible products. Analysis (Method 3) were carried out to find the most possible route.

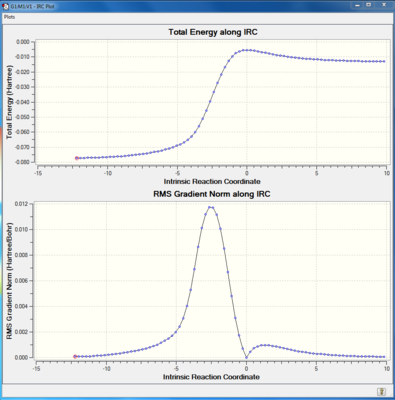
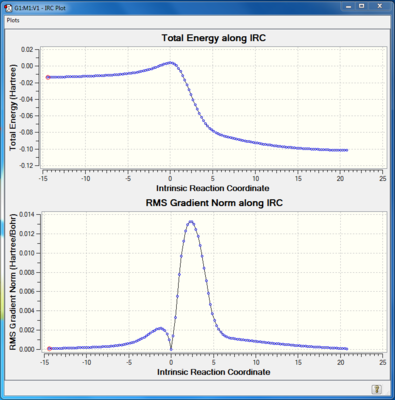
IRC calculation

Table 9. Transition state IRC
	Endo Transition state	Exo Transition state	Cheletropic Transition state
IRC animation (click the image to show the animation)	Fig. 28 Endo IRC animation	Fig. 30 Exo IRC animation	Fig. 32 Cheletropic IRC animation
IRC trajectory	Fig. 29 Endo IRC	Fig. 31 Exo IRC	Fig. 33 Cheletropic IRC

IRC calculations were done to the transition states of three possible pathways. The total energy along IRC graph showed the activation energy of a reaction, which was lower than that in exercise 1. This behaviour was due to the presence of an unstable reactant, xylyene. Xylyene had 4 π electrons in the ring, which is antiaromatic, thus very unstable. The product of the cycloaddition reaction was aromatic, so the driving force of the forward reaction was the stabilisation energy.

(The energy shown on the IRC is the electronic energy Tam10 (talk) 11:29, 21 February 2018 (UTC))

Also, Diels-Alder reaction required a cis arrangement of double bonds. The structure of xylyene had a fixed shape, so there was no equilibrium with its trans isomer, which further helped the cycloaddition. Bond lengths measured in xylyene were C=C 1.35 Å, C-C 1.46 Å, 1.47 Å and 1.49 Å. In the six-membered ring product, C-C changed to 1.47 Å. This value was in between C-C (1.54 Å) and C=C (1.34 Å), which was due to delocalisation of π electrons in the ring system.

Reaction barrier

Table 10. Gibbs free energy at PM6 level
Molecule	Gibbs free energy (Hatree)	Gibbs free energy (kJ/mol)
Xylylene	0.178047	467.462434
SO2	-0.119268	-313.1381579
Exo TS	0.092078	241.750807
Endo TS	0.090561	237.767924
Cheletropic TS	0.099062	260.087301
Exo product	0.021454	56.3274813
Endo product	0.021697	56.96547784
Cheletropic product	-0.000002	-0.0052510004

Table 11. Activation energy and Reaction energy
	Exo Diels-Alder product	Endo Diels-Alder product	Cheletropic product
Activation energy / kJmol-1	87.4265309	83.4436479	105.7630249
Reaction energy / kJmol-1	-97.9967948	-97.35879826	-154.3295271

(Your SO2 is curiously low in energy Tam10 (talk) 11:29, 21 February 2018 (UTC))

Exercise 3 shows a reaction between xylene and sulphur dioxide. There were two possible routes. One is hetero-Diels-Alder reaction between xylyene (diene) and sulphur dioxide (dienophile), the other is Cheletropic reaction. The hetero-Diels-Alder reaction generates two possible products. Analysis (Method 3) were carried out to find the most possible route.

Reaction profile

From the reaction profile, all three reactions were exothermic. The energies of transition states and products were indicated in the profile. The Cheletropic reaction required the highest activation energy, but formed the most stable product (the lowest energy). The activation energy of Endo Diels-Alder reaction was the lowest, but the product was most unstable. Exo Diels-Alder reaction had medium activation energy and product energy. Based on the reaction profile, under kinetic condition, the reaction favoured Endo Diels-Alder, which required lowest activation energy, and under thermodynamic condition, the reaction favoured Cheletropic reaction which generates the most stable product. Endo and Exo Diels-Alder reactions had similar activation energy and product energy.

(You should normalise your profile to the reactant energy Tam10 (talk) 11:29, 21 February 2018 (UTC))

Calculation for exercise 3

PM6 optimized endo transition state: File:Exercise3-PRODUCT-ENDO-TS1-LWY.LOG

PM6 optimized exo transition state: File:Exercise3-PRODUCT-EXO-TS1-LWY.LOG

PM6 optimized cheletropic transition state: File:Exercise3-CHELETROPIC-TS1-LWY.LOG

PM6 optimized endo transition state IRC: File:Exercise3-ENDO-IRC-LWY.LOG

PM6 optimized exo transition state IRC: File:Exercise3-EXO-IRC-LWY.log

PM6 optimized cheletropic transition state IRC: File:Exercise3-Cheletropic-irc-LWY.log

PM6 optimized endo product: File:Exercise3-PRODUCT-ENDO-OPT-LWY.LOG

PM6 optimized exo product: File:Exercise3-PRODUCT-OPT-LWY.LOG

PM6 optimized cheletropic product: File:Exercise3-CHELETROPIC-OPT-LWY.LOG

Conclusions

In this computational lab, Gaussian was used to determine the transition state of three pericyclic reactions. The optimization started from the product, broke the bonds which formed in the forward reaction, froze them, and then optimized to transition state. Further IRC and frequency calculations were used to confirm the correct transition states.

For exercise 2 and 3, the reaction MO were visualised and analysed. Only MOs of same symmetry can overlap. Single point energy calculation yields the energy of HOMO and LUMO, which further determined if the Diels-Alder reaction was normal or inverse demand.

Activation energies and reaction energies were calculated for each reaction. Under kinetic condition, the pathway which had lowest activation energy proceed; under thermodynamic condition, the pathway which generates lowest energy product proceed.