Rep:SL7514TransitionStates

Introduction

For a molecule consisting of N number of atoms, it is possible to assign a general set of cartesian coordinates for each atom. This would result in a total number of $3N_{atoms}$ possible coordinates. However, the global translation and rotation must be taken into account as they do not affect the energy of the molecule. Translation of the whole molecule along or rotation about any of the axes will not affect the total energy. Therefore, the molecule has total number of $3N_{atoms}-6$ degrees of freedom and hence the potential energy surface is a multivariable function of $3N_{atoms}-6$ variables.

Figure 1. It is possible to assign Cartesian coordinates to all atoms in the molecule.

By taking the Taylor expansion of the potential function, it is possible to find the Hessian matrix of function with n variables $f(x_1,x_2,...,x_n)$:

$\mathbf{H}=\left[\begin{array}{cccc}\frac{{\partial }^{2}f}{\partial x_1^2}& \frac{{\partial }^{2}f}{\partial x_1\partial x_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_1\partial x_n}\\ \frac{{\partial }^{2}f}{\partial x_2\partial x_1}& \frac{{\partial }^{2}f}{\partial x_2^2}& \cdots & \frac{{\partial }^{2}f}{\partial x_2\partial x_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{{\partial }^{2}f}{\partial x_n\partial x_1}& \frac{{\partial }^{2}f}{\partial x_n\partial x_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_n^2}\end{array}\right]$

Local maximum and minimum can be found by equating the first order differential (gradient) of the potential function to zero. These points correspond to locations on the potential energy surface where the net force on the molecule is zero.

$$\begin{gathered} \frac{\partial f}{\partial x_1}=0, \\ \frac{\partial f}{\partial x_2}=0, \\ ..., \\ \frac{\partial f}{\partial x_n}=0 \end{gathered}$$

The transition state correspond to the saddle points in the potential energy surface. The coordinates for the saddle points are found where the determinant of the Hessian matrix is less than zero (gradient = 0, curvature < 0).

$\det (\mathbf{H})<0$

If the determinant is greater than zero, than the points correspond to either maximum or minimum. The minimum, or the stable equilibrium of the multivariable function is found where all the eigenvalues of the Hessian matrix is positive (gradient = 0, curvature > 0). From the Sylvester's criterion, the Hessian matrix is positive definite if all the leading principal minors are positive.

Each vibrational modes in the molecule correspond to a normal mode. The multivariable Taylor expansion of the potential shows that the second derivatives correspond to the force constant, forming the Hessian matrix.

$V=V(0)+\sum _i{\left(\frac{\partial V}{\partial x_i}\right)}_0{x}_i+\frac{1}{2}\sum _{i,j}{\left(\frac{{\partial }^{2}V}{\partial x_i{x}_j}\right)}_0{x}_i{x}_j+...$

let

$k_{i,j}=\left(\frac{{\partial }^{2}V}{\partial x_i{x}_j}\right)$

If $k_{i,j}\ne 0$ where $i\ne j$, then the vibrations are coupled. The vibrational modes correspond to normal coordinates which diagonalise the Hessian matrix.

$\left[\begin{array}{ccc}{k}_{11}& k_{12}& \cdots \\ k_{21}& k_{22}& \\ ⋮& & k_{(3N-6)(3N-6}\end{array}\right]$ → $\left[\begin{array}{ccc}{\kappa }_{11}& 0& \cdots \\ 0& {\kappa }_{22}& \\ ⋮& & {\kappa }_{(3N-6)(3N-6)}\end{array}\right]$

If one of the vibrational mode is negative, then one of the direction in the normal coordinate system has a energy maximum and all other orthogonal direction has minimum. This is the reason why the vibration with the negative frequency must correspond to the reaction pathway. If all vibrational modes are positive then all orthogonal directions in the normal coordinate have energy minimum and therefore this corresponds to the local minima.

Nf710 (talk) 21:53, 21 March 2017 (UTC) This is a fantastic intro. excellent mathematical understanding. The last sentence is missing that the first derivatives must be zero also thereby satisfying the second partial derivative test for a local maximum.

Reaction of Butadiene with Ethylene

All of the optimised product, reactants and transition states in this experiment are outlined below:

Molecule 1. Optimised diene used to optimise the transition state			Molecule 2. Fully optimised diene			Molecule 3. Fully optimised ethene			Molecule 4. Freeze bond optimisation for diene and ethene
Molecule 5. Transition state optimisation for diene and ethene			Molecule 6.IRC for Diels-Alder reaction betweem diene and ethene			Molecule 7.Initial optimisation of the final product			Molecule 8.Fully optimised final product after distortion

The MO diagram for the formation of the butadiene and ethene transition state is shown in Figure 2. The relative energies of the fragment orbitals were found using the literature.. Figures 3 to 10 shows the MO surface calculations from Gaussian on PM6 level. The MOs diagrams corresponding to each MO surface from Gaussian calculations are labelled on the diagram in Figure 2 as MO16, MO17 etc. It should be noted that the HOMO and LUMO energy of the diene and ethene are expected to be similar as no electron withdrawing group or electron donating groups are present on ethene or diene.

Figure 2. The MO diagram for the reaction of butadiene with ethene

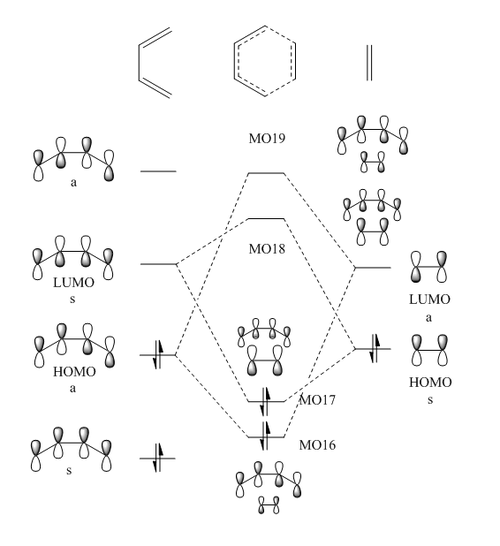
(Fv611 (talk) 17:54, 15 March 2017 (UTC) Good MO diagram, but you are missing the symmetry labels on the transition state MOs.)

Figure 3. HOMO of optimised diene			Figure 4. LUMO of optimised diene
Figure 5. HOMO of optimised diene			Figure 6. LUMO of optimised diene
Figure 7. MO16 of the transition state for the Diels-Alder reaction between diene and ethene			Figure 8. MO17 of the transition state for the Diels-Alder reaction between diene and ethene
Figure 9. MO18 of the transition state for the Diels-Alder reaction between diene and ethene			Figure 10. MO19 of the transition state for the Diels-Alder reaction between diene and ethene

In molecular orbital theory, the molecular orbitals (MOs) are formed from linear combination of atomic orbitals (AOs) or fragment orbitals (FOs). For two AOs or FOs wavefunctions ${\psi }_1$ and ${\psi }_2$ there are two possible linear combinations:

${\mathrm{\Psi }}_T=c_1{\psi }_1+c_2{\psi }_2$

${\mathrm{\Psi }}_T^{*}=c_1{\psi }_1-c_2{\psi }_2$

In a bonding interaction, the sign of the coefficient for each AOs or FOs are the same, leading to bonding molecular orbital ${\mathrm{\Psi }}_T$. In an antibonding interaction, the sign of the coefficient for each AOs or FOs are opposite, leading to antibonding molecular orbital ${\mathrm{\Psi }}_T^{*}$. In bonding interaction, electron density is present between the atoms or molecular fragments and hence leads to lowering of the energy of the formed MO. In antibonding interaction, the bond is weakened and hence leads to raising of the energy of the formed MO. It is therefore important to consider the interaction of AOs and MOs in bonding and antibonding pairs.

Figure 11. MO diagram to illustrate the possible linear combinations for symmetric-symmetric, symmetric-antisymmetric and antisymmetric-antisymmetric interactions

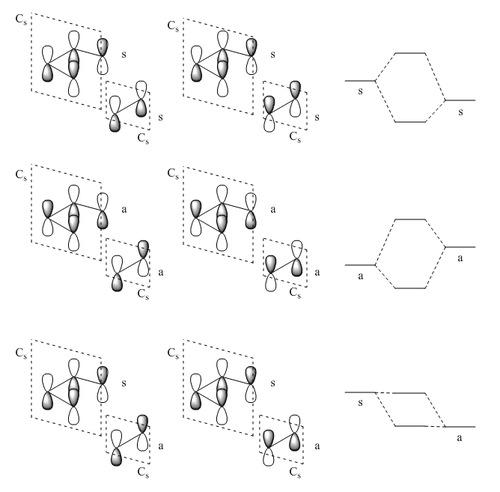
For this Diels-Alder reaction to be allowed, the plane of symmetry must be preserved as it can be seen on Figure 11, and hence the ethylene fragment should approach the diene from one face. The reaction would be disallowed if the ethene fragment approaches the diene at an angle which does not preserve the plane of symmetry. Furthermore, both HOMO-LUMO interactions are allowed by symmetry as this results in one bonding interaction since it is possible for both fragments to approach in phase.

As discussed before, to qualitatively determine the orbital overlap integral, both linear combinations must be considered where the coefficient of FOs have been swapped. As illustrated in Figure 11, for symmetric-symmetric and antisymmetric-antisymmetric interactions, there is a clear one bonding interaction and one antibonding interaction leading to one bonding orbital and one antibonding orbital. Therefore, the orbital overlap integral is expected to be non-zero. For the symmetric-antisymmetric case, there is a one bonding and one antibonding interaction within the same fragment. When the orbital coefficient is swapped, there is still one bonding and one antibonding interaction within the same fragment and therefore, orbital overlap integral is expected to be zero.

(Fv611 (talk) 17:54, 15 March 2017 (UTC) You are not stating that only AS/AS and S/S combinations are allowed)

Figure 12. IRC and the gradient plot for the Diels-Alder reaction between diene and ethene

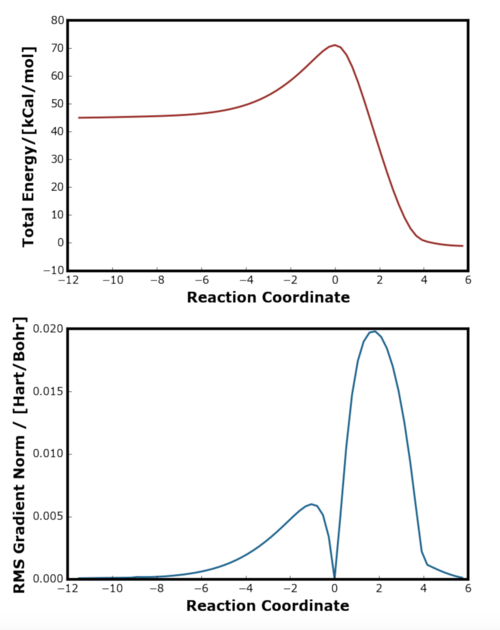
The IRC plot showed a successful reaction pathway as the gradient was found to be zero at the coordinates corresponding to transition state, reactant and products. The reaction barrier was found to be 26.2 kCal mol^-1 which agreed well with the literature calculation

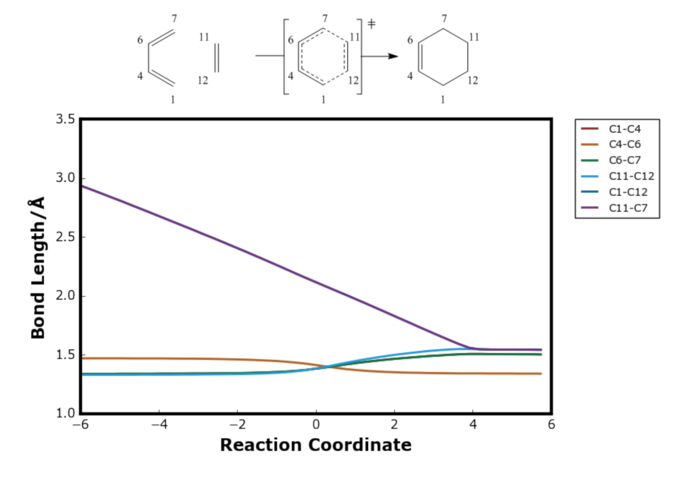
The plot below illustrates the change in carbon-carbon bond distanced during the Diels-Alder reaction, obtained from this experiment.

Figure 13. Change in C-C bond distances during the Diels-Alder reaction, obtained from this experiment

Table 1. A summary of the C-C bond lengths from literature

Bond Type	Bond Length / Å
Sp3 - Sp3	1.54
Sp3 - Sp2	1.50
Sp2 - Sp2 (single)	1.47
Sp2 - Sp2 (double)	1.34

Table 2. A summary of the C-C bond lengths obtained from this experiment

Bond Type	Transition State Bond Length / Å	Reactants Bond Length / Å	Products Bond Length / Å
C1-C4	1.380	1.335	1.501
C4-C6	1.411	1.468	1.338
C6-C7	1.380	1.335	1.501
C11-C12	1.382	1.327	1.541
C1-C12	2.115	3.415	1.540
C11-C7	2.115	3.414	1.540

(Fv611 (talk) 17:54, 15 March 2017 (UTC) Including the butadiene-ethylene bond lenghts in the reactants makes it look like they are always bonded.)

Comparing Table 1 and Table 2, the reactant and product bond lengths obtained from the calculation matched the literature results very well. At the transition state, all the C=C double bonds (C1-C1, C6-C7 and C11-C12) elongated, and the single bond (C4-C6) was shortened compared to the reactants. The inter-molecular bonds (C1-C12 and C11-C7) remained the longest. As it can be seen from Figure 12, the electron density in these bonds are smallest in the transition state and hence was expected to be the longest. It should also be noted that the bond length C4-C6 and C11-C12 cross over each other after the reaction coordinate 0 where the transition state was optimised. This suggested that the transition state at coordinate zero resembled the reactants more than the products meaning the reaction went via early transition state from Hammond's postulate.

The van der Waals radius for carbon was found to be 1.70 Å . The van der Waals radius is the half the internuclear separation of two atoms of the same element at their closest possible approach without forming a bond. Therefore, the closest possible carbon-carbon distance without forming a bond is 3.40 Å, if all atoms are modeled as hard-spheres. From Table 2, it can be seen that all carbon-carbon distances were shorter than this value which suggest there are bonding interaction between all carbons listed in the table.

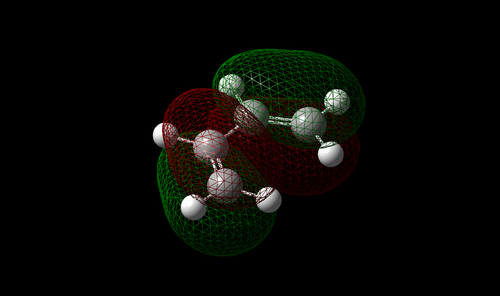
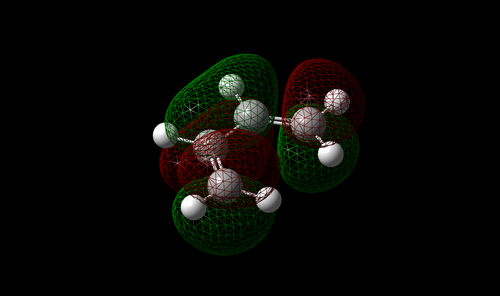
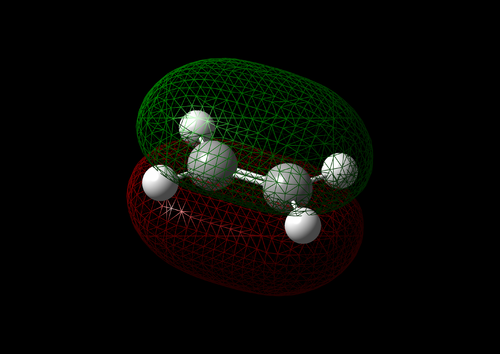
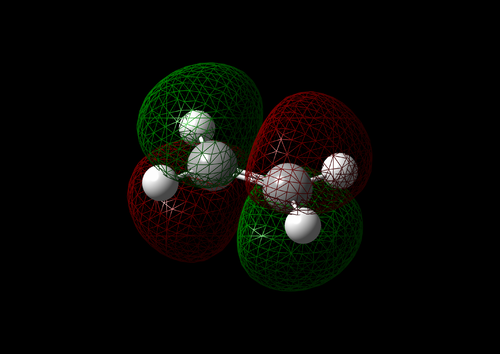
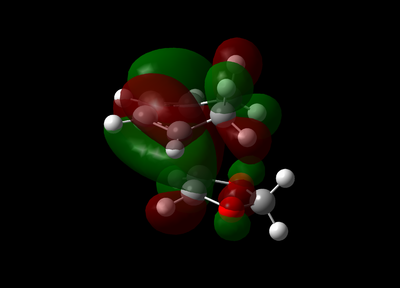
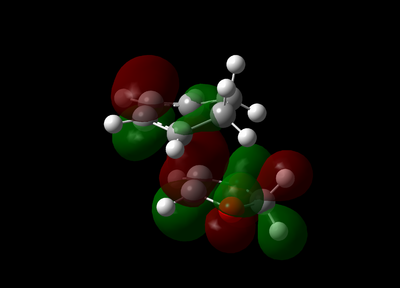
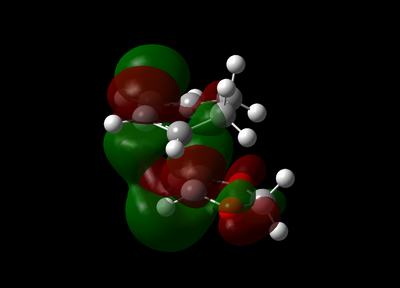
The vibration with the negative frequency must correspond to the reaction pathway. This vibrational mode is illustrated in Molecule 5. The vibration was symmetrical where the two carbons at the opposite ends of the diene approached the two carbons on ethene simultaneously. The bond formation in this Diels-Alder reaction was a concerted process. This finding agreed with the literature where the study by Houk et al predicted synchronous bond formation in Diels-Alder reaction using Hartree-Fock method in favour of di-radical mechanism.

Reaction of Cyclohexadiene and 1,3-Dioxole

All of the optimised product, reactants and transition states for the Endo Diels-Alder experiment are outlined below:

Molecule 9. Optimised cyclodiene at PM6 level			Molecule 10. Optimised cyclodiene at B3LYP(d) level			Molecule 11. Cyclodiene distorted and re-optimised at B3LYP(d) level			Molecule 12. 1,3-Dioxole optimised at PM6 level
Molecule 13. 1,3-Dioxole optimised at B3LYP(d)level			Molecule 14.1,3-Dioxole distorted and re-optimised at B3LYP(d)level			Molecule 15. Freeze coordinate minimisation for the transition state of Endo reaction at PM6 level			Molecule 16. Freeze coordinate minimisation for the transition state of Endo reaction at B3LYP(d) level
Molecule 17. Transition state optimisation for Endo at PM6 level			Molecule 18. Transition state optimisation for Endo at B3LYP(d) level			Molecule 19. IRC calculation for Endo transition at PM6 level			Molecule 20. Optimisation of the Endo product at PM6 level
Molecule 21. Optimisation of the Endo product at B3LYP(d) level

All of the optimised product, reactants and transition states for the Exo Diels-Alder experiment are outlined below:

Molecule 22. Freeze coordinate minimisation for Exo reaction at PM6 level			Molecule 23. Freeze coordinate minimisation for Exo reaction at B3LYP(d) level			Molecule 24. Transition state optimisation for the Exo reaction at PM6 level			Molecule 25. Transition state optimisation for the Exo reaction at B3LYP(d) level
Molecule 26. IRC calculation for the Exo reaction at PM6 level			Molecule 27. Exo product optimisation at PM6 level			Molecule 28. Exo product optimisation at B3LYP(d) level

(Some of these geometries aren't too necessary to put in the main body of the report. They can be included as supplementary information Tam10 (talk) 12:23, 23 March 2017 (UTC))

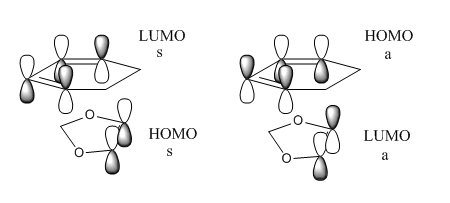
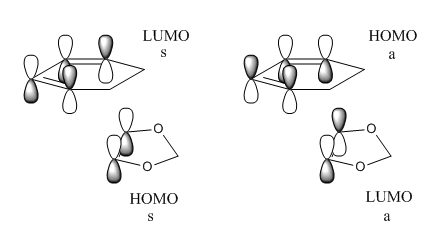
The MOs associated with this Diels-Alder reaction are shown below. The HOMO and LUMO orbitals corresponds to Figures 16 to 19.

Figure 14. Frontier Molecular Orbitals for Endo Diels-Alder reaction

Figure 15. Frontier Molecular Orbitals for Exo Diels-Alder reaction

The MOs calculated from Gaussian are shown below for both Endo and Exo reactions.

Figure 16. HOMO of 1,3-Dioxole (symmetric)			Figure 17. LUMO of 1,3-Dioxole (antisymmetric)			Figure 18. HOMO of Cyclohexadiene (antisymmetric)
Figure 19. LUMO of Cyclohexadiene (symmetric)			Figure 20. MO40 of the transition state for the Endo Diels-Alder reaction between cyclohexadiene and 1,3-dioxole (antisymmetric)			Figure 21. MO41 of the transition state for the Endo Diels-Alder reaction between cyclohexadiene and 1,3-dioxole (symmetric)
Figure 22. MO42 of the transition state for the Endo Diels-Alder reaction between cyclohexadiene and 1,3-dioxole (symmetric)			Figure 23. MO43 of the transition state for the Endo Diels-Alder reaction between cyclohexadiene and 1,3-dioxole (antisymmetric)			Figure 24. MO40 of the transition state for the Exo Diels-Alder reaction between cyclohexadiene and 1,3-dioxole (antisymmetric)
Figure 23. MO41 of the transition state for the Exo Diels-Alder reaction between cyclohexadiene and 1,3-dioxole (symmetric)			Figure 24. MO42 of the transition state for the Exo Diels-Alder reaction between cyclohexadiene and 1,3-dioxole (symmetric)			Figure 25. MO43 of the transition state for the Exo Diels-Alder reaction between cyclohexadiene and 1,3-dioxole (antisymmetric)

The transition state, reactants and products were confirmed by the frequency analysis. At the transition state, one negative frequency was observed at -529 cm^-1 and -521 cm^-1 for Exo and Endo reactions respectively.

In order to determine whether the electron demand was normal or inverse for this Diels-Alder reaction, energy optimisation was performed at B3LYP/6-31G(d) for the initial reactants. The alkene in this reaction possessed electron donating groups and qualitatively, would increase the HOMO and LUMO of the dienenophile. Therefore, intuitively inverse electron demand Diels-Alder was expected.

Figure 26. Expected MO diagram for normal electron demand Diels-Alder reaction

Figure 27. MO diagram constructed following the Gaussian calculation at B3LYP/6-31G(d) level

(This is actually the typical MO diagram for an inverse demand. The HOMO at the TS should be antisymmetric Tam10 (talk) 12:23, 23 March 2017 (UTC))

Figure 26 and 27 compares the expected MO diagram for normal electron demand and the MO diagram constructed for the Exo Diels-Alder reaction. Figure 26 represents a normal electron demand since the energy matching between ethene LUMO and diene HOMO is much better than ethene HOMO and diene LUMO and hence, resulting in stronger interaction. Therefore, the ethene is expected to have greater electron accepting character and diene have greater electron donating character.

Figure 27 showed the relative energies of the HOMOs and LUMOs in Hartree for this experiment. It was clear that energy matching between the HOMO of the ethene and the LUMO of the diene was much better than the LUMO of ethene and HOMO of diene. Therefore, the ethene was expected to have greater electron donating character and diene was expected to have greater electron accepting character. As predicted by the organic chemistry intuition, the MO calculation supported the argument that the reaction was inverse electron demand. It was not possible determine the electron demand by comparing the relative energies of the MOs from the transition state. The energy difference between the HOMO and HOMO-1 and LUMO and LUMO+1 was too similar to justify the electron demand was changed.

It is worth noting that different DFT calculation can potentially lead to differing results. B3LYP method utilised the Kohn-Sham method, where it was approximated that N electrons do not interact with each other. Therefore, DFT method was approximate and this was also the reason why it was not possible to quantitatively compare the energy values of the MOs.

Nf710 (talk) 22:00, 21 March 2017 (UTC) B3LYP is a hybrid mode which, uses HF to calculate the exchange correlation. Different DFT functionals treat the exchange correlation differently. DFT in theory can solve everything apart from this term in the Hamiltonian exactly. (The non interacting part)

Table 3. A summary of the energy output from Diels-Alder reaction between cyclohexene and 1,3-dioxole

	Endo	Exo
Activation Barrier ΔGǂ	72.03	79.85984
Product Free Energy Change ΔrG	-155.18281	-151.5885

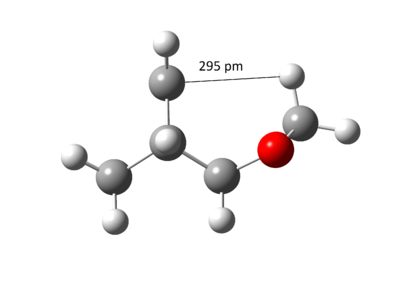
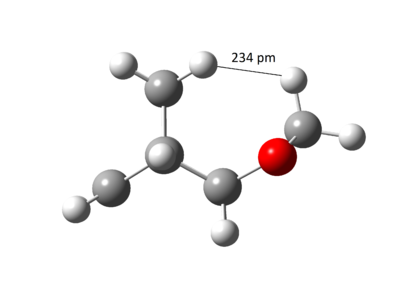
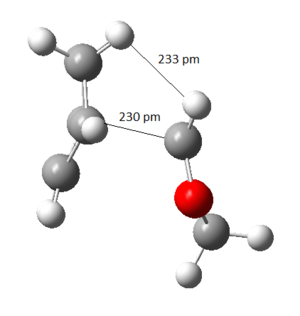
The free energy change was calculated by finding the difference in absolute free energy between sum of reactants with transition state and the product from Gaussian calculation at B3LYP/6-31(d). This experiment predicted the Endo product to be both kinetic and thermodynamic product because the activation energy barrier and the Gibbs free energy change for the reaction was lower. This was contradictory from usual Diels-Alder reaction where the Exo product was expected to be the thermodynamic product. . The reasoning came by studying the sterics of the ring clash within the molecule as illustrated in Figure 28 and 29. The nearest distance between the dioxole ring and cyclohexene ring in Exo was 234 pm compared to 295 pm in Endo and therefore, the Endo product was more favoured due to the steric clash.

Figure 28. Steric interaction in Endo Diels-Alder product

Figure 29. Steric interaction in Exo Diels-Alder product

Figure 30. Secondary orbital overlap was possible in Endo Diels-Alder reaction

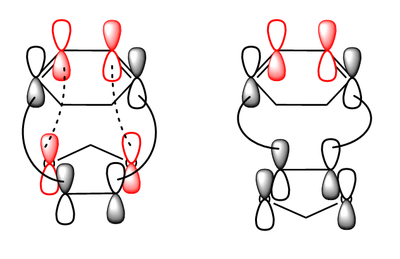
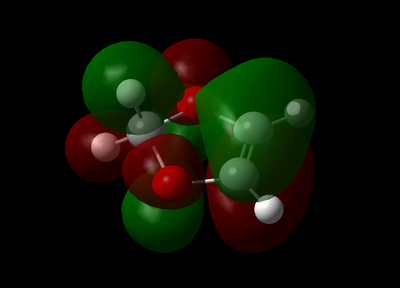
The reason why the activation energy barrier for the endo product was because of the secondary orbital overlap. The oxygen atoms in 1,3-Dioxole was Sp³ hybridised and hence the lone pair electrons were in the p orbital. Figure 30 below illustrated how these p orbital could favourably overlap with the MO in the cyclohexadiene in Endo, lowering the transition state energy. This interaction was not possible for the Exo transition state leading to higher activation energy barrier. MO 41 and MO 43 in the Endo transition state (Figure 21 and 23) clearly illustrated this interaction as mixing was observed between the p orbitals from the oxygen with the diene. Steric effects were also analysed for both transition states. The closest distance between other atoms (other than the carbon atoms involved in the transition states) was longer than the distance between the carbon atoms directly involved in the reaction. Therefore, steric had a negligible effect on the reaction energy barrier and the secondary orbital interactions were the main contributor for the Endo product being the kinetic product.

Figure 30. Illustration of possible steric clash in Exo transition state

Figure 31. Illustration of possible steric clash in Exo transition state

Nf710 (talk) 22:04, 21 March 2017 (UTC) This section was done excellently, your energies were slightly out on the calculation. But everything else was done excellently.

Diels-Alder and Cheletropic Reaction

The IRC plot for Endo, Exo and Cheletropic reaction between Xylylene and SO₂ are shown below.

Figure 32. IRC and gradient plot for Cheletropic, Endo and Exo Diels-Alder reaction between xylylene and SO2. The primary orbital interactions are shown by the solid line and the secondary by the dashed line.

(Don't overlap IRCs like this. They are coordinates projected in different directions from different starting points. The result of forcing them into one coordinate is confusing. Instead, draw straight lines from the relative energies to the stationary points. This way, you are making no assumptions about the gradient at any point, or the "distance" to the TS Tam10 (talk) 12:23, 23 March 2017 (UTC))

The IRC movie for Endo, Exo and Cheletropic reaction between Xylylene and SO₂ are shown below.

Figure 33. Cheletropic reaction between xylylene and SO2 visualisation

Figure 34. Endo Diels-Alder reaction between xylylene and SO2 visualisation

Figure 35. Exo Diels-Alder reaction between xylylene and SO2 visualisation

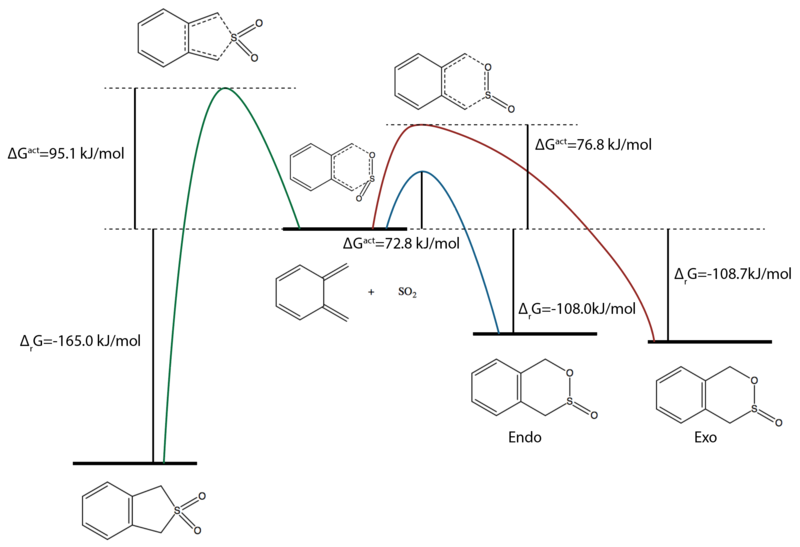
The reaction profile diagram for this experiment is shown in Figure 36.

Figure 36. The reaction profile diagram for the Endo, Exo Diels-Alder reaction and Cheletropic reaction between Xylylene and SO2

(This is better in terms of the x-axis than before, but there are still issues about curves. It's worse however in terms of the gradients. You mustn't draw curves as you are showing a gradient which in this case is entirely fictional. Tam10 (talk) 12:23, 23 March 2017 (UTC))

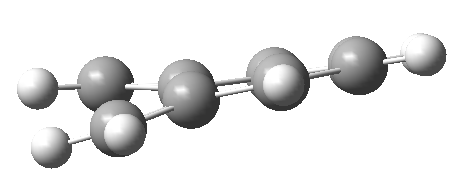
Following the reaction, the 6-membered ring becomes aromatic as it satisfy the Huckel's rule 4n+2 electrons in continuous p orbitals on a flat surface in a ring. Xylylene is very unstable molecule since it is antiaromatic. Antiaromatic compounds possess 4n π electron system and since Xylylene has 8 π electrons, the electron interactions in the π system is highly unfavourable and the molecule is usually heavily distorted. Indeed, optimised xylylene using B3LYP/6-31(d) basis set showed this distortion.

Figure 37. Antiaromatic distortion in Xylylene optimised at B3LYP/6-31(d) level

The experimental literature review showed that above 50^οC, formation of sulfolenes were highly favoured whereas below 50^οC sultines were formed. This agreed very well with the reaction profile diagram in Figure 36. At high temperature, the reaction is thermodynamically controlled, and hence the cheletropic reaction and the formation of sulfolene were favoured. At lower temperatures, the reaction was kinetically controlled and the reaction pathway with lower activation energy barrier (Diels-Alder) reaction was favoured.

Table 4. A summary of the activation energy and the change in free energy for the Diels-Alder reaction at the cyclohexadiene part of the molecule compared to the end diene part

	Endo Cyclohexadiene Part	Exo Cyclohexadiene Part	Endo End Part	Exo End Part
Activation Barrier ΔGǂ	103.0	110.8	72.8	76.8
Product Free Energy Change ΔrG	7.3	11.7	-108.0	-108.7

Table 4 summarised the free energy changes that occurred during the reaction for the Diels-Alder at the end diene and cyclohexadiene. The reaction at the cyclohexadiene part of the molecule was kinetically unfavoured due to much higher activation energy barrier. Furthermore, the free energy change for the product formation was positive and hence it was unfavourable for the reaction to proceed. The formed product was more likely to split back to its reactant form under thermodynamic conditions.

Molecule 29. Initial optimisation of the product			Molecule 30. Freeze coordinate energy minimisation for the Endo product			Molecule 31. Freeze coordinate energy minimisation for the Exo product			Molecule 32. Freeze coordinate energy minimisation for the cheletropic reaction
Molecule 33. Transition state optimisation for the Endo reaction			Molecule 34. Transition state optimisation for the Exo reaction			Molecule 35. Transition state optimisation for the Cheletropic reaction			Molecule 36. IRC for the Endo Diels-Alder reaction
Molecule 37. IRC for the Exo Diels-Alder reaction			Molecule 38. IRC for the Cheletropic reaction			Molecule 39. Endo product optimisation			Molecule 40. Exo product optimisation
Molecule 41. Cheletropic product optimisation			Molecule 42. Endo freeze coordinate minimisation for the Diels-Alder reaction at the cyclohexadiene position			Molecule 43. Exo freeze coordinate minimisation for the Diels-Alder reaction at cyclohexadiene position			Molecule 44. Initial product optimisation for the Endo Diels-Alder reaction at the cyclohexadiene position
Molecule 45. Initial product optimisation for the Exo Diels-Alder reaction at the cyclohexadiene position			Molecule 46. Transition state optimisation for the Endo Diels-Alder reaction at the cyclohexadiene position			Molecule 47. Transition state optimisation for the Exo Diels-Alder reaction at the cyclohexadiene position			Molecule 48. Product optimisation for the Endo Diels-Alder reaction at the cyclohexadiene position
Molecule 49. Product optimisation for the Exo Diels-Alder reaction at the cyclohexadiene position			Molecule 50. IRC calculation for Endo Diels-Alder reaction at the cyclohexadiene position			Molecule 51. IRC calculation for Exo Diels-Alder reaction at the cyclohexadiene position

Extension

Introduction

For ring closing electrocyclic reactions, the ring closure can be either conrotatory or disrotatory. From Woodward-Hoffmann rules, for thermally allowed pericyclic reactions the stereospecificity is determined by the symmetry of the HOMO. In this study, the ring closing pericyclic reaction in the formation cyclobutene was investigated. The unusual stereochemical outcome was first investigated by Vogel in 1958. As shown in Figure 36, due to the symmetry of the HOMO only the conrotatory reaction is allowed via Mobius transition state involving one antarafacial component.

Figure 38. Conrotatory vs disrotatory reaction in the formation of cyclobutene

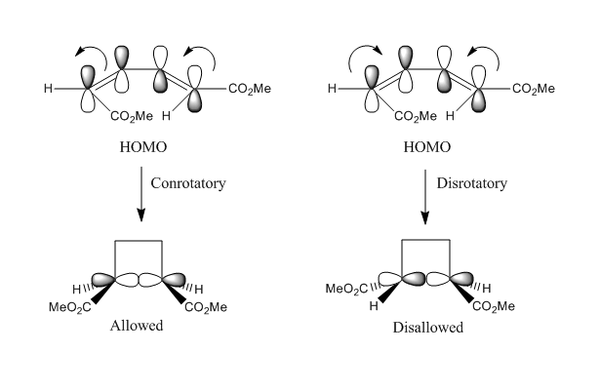
Photochemical reaction would proceed via opposite stereochemistry. The excitation of the electron from the HOMO to LUMO would produce a triplet excited state with the reaction proceeding from the LUMO. The phase of the orbital in the FOs has now been reversed and hence the electrocylic reaction of butene would proceed via disrotatory path with Hückel transition state involving suparafacial component. There were many research already performed in this field and conical interactions connecting different electronically excited states was the believed pathway in photochemical reactions.

Figure 39. Disrotatory path is favoured in photochemical reaction

Methodology

Molecule 52. Initial optimisation of the product			Molecule 53. Freeze coordinate energy minimisation
Molecule 54. Conrotation transition state			Molecule 55. IRC for the conrotation reaction

The product was initially optimised using Gaussview at PM6 level. The initial guess for the transition state was made by elongating the C-C bond which forms during the reaction to 2.2 Ǎ and manually rotating the substituents. The four bonds in the cyclobutene ring was kept constant by freezing the bond length and the angle. The transition state was found using the PM6 method, following which the IRC calculation was performed.

Results and Discussion

The simulation for this reaction is shown below as the gif in Figure 40.

Figure 40. Reaction pathway for the conrotatory reaction

Figure 41. Conrotatory vs disrotatory reaction in the formation of cyclobutene

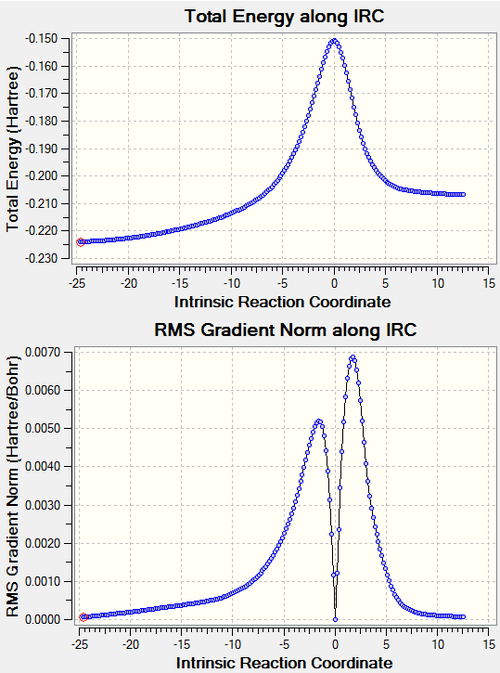
IRC analysis showed the expected reaction pathway with a clear transition state and product energy higher than the reactant due to the ring strain. The activation energy barrier and the free energy change for the reaction was found to be 200.9 kJ/mol and 60.6 kJ/mol respectively.

It was unfortunately not possible to investigate the conical intersection for the photochemical reaction. The B3LYP/6-31(d) basis set was too time consuming to model and perform IRC at the first excited state. With the lower basis set it was not possible to accurately model the MOs required for CASSCF computation.

(Very good mini-study. You have made a good proof of WH rules for anti-aromatic systems, with a nice justification. As you have said, optical excitation would indeed result in disrotation. You have used Gaussian as a learning tool to help understand aromaticity and WH rules +20% Tam10 (talk) 12:23, 23 March 2017 (UTC))