Rep:SL629

Year 3 Computation Lab: Transition State Exercises

Introduction

The aim of this exercise is to understand the transition structures of different pericyclic reactions in the potential energy surface (PES) using Gaussview. PES is a plot of the energy of two or more reactants with respect to the positions of the molecules, which represents the molecular geometry of the system . Each local minimum of the PES represents a stable conformer. The most stable structure is therefore the global minimum of the whole PES. Yet, optimization in Gaussview does not result in the global minimum, instead, it optimizes to the “nearest” local minimum structure. Local minima have two requirements: 1) they are stationary points--zero gradient in all directions, i.e.the first derivative is zero with respect all geometric coordinates (see Equation 1), and 2) positive curvature, i.e. positive second derivative with respect all geometric coordinates (see Equation 2):

$\frac{\partial E}{\partial q_1}=\frac{\partial E}{\partial q_2}=\frac{\partial E}{\partial q_3}=\dots =0$	(Eq.1)
$\frac{{\partial }^{2}E}{\partial q_n^2}>0\text{, n=1,2,3...}$	(Eq.2)

Between any two minima, there is a lowest energy pathway, known as the reaction coordinate or intrinsic reaction coordinate (IRC). This pathway has the smallest activation barrier for the molecules to go from one minimum to another. The saddle point on the IRC is the structure with the maximum energy, which represents the transition state structure. At transition state, the first derivative of potential energy is also zero. However, as the maximum of the IRC, it has at least one negative curvature with respect to one geometric coordinate, which is the IRC. (Transition state with more than one negative curvature are higher order saddle points—transition state of more than one IRC.) The negative curvature is the characteristic used to differentiate between stable conformers and transition state geometries. Curvature of the PES, which is the second derivative of the potential energy, is in fact the force constant k of the geometry (see Equation 3):

$k=\frac{{\partial }^{2}E}{\partial q_n^2}\text{, n=1,2,3...}$

(Eq.3)

This force constant is related to the vibrational frequency of the corresponding structure by Equation 4:

$\nu =\frac{1}{2}\pi \sqrt{\frac{k}{\mu }}\text{, where }\mu \text{ is the reduced mass of the molecule.}$

(Eq.4)

When curvature is negative, meaning k is negative, the vibrational frequency becomes the square root of a negative number, leading to an imaginary frequency. Thus, the presence of imaginary frequency is used to confirm the geometry as the transition state geometry.

Nf710 (talk) 23:10, 15 December 2016 (UTC) Excellent use of equations to explain the principles

Exercise 1: Reaction of Butadiene with Ethylene

The reaction of butadiene and ethylene is a Diels-Alder reaction, which is a cycloaddition reaction with butadiene as the conjugated diene and ethylene as the dienophile. In these type of reactions, the diene must be the cis-conformation to interact with the dienophile, so butadiene is first optimized to the cis-conformation. As it is well-known as a concerted reaction, where the two terminal carbons of diene forms two bonds with the carbons on ethylene at the same time. Therefore, for the analysis of this reaction, a guessed transition state was generated, with the ethylene carbons placed under the terminal carbons of butadiene, and the coordination of each bond-forming pairs of carbons fixed.

Orbital interactions

Figure 1.1-1.4 shows the HOMO and LUMO of butadiene and ethylene, optimised at the PM6 level.

Fig 1.1 Butadiene HOMO

Fig 1.2 Butadiene LUMO

Fig 1.3 Ethylene HOMO

Fig 1.4 Ethylene LUMO

As a short summary of the symmetries of the frontier orbitals of butadiene and ethylene,
Symmetric molecular orbitals: LUMO of butadiene, HOMO of ethylene;
Asymmetric molecular orbitals: HOMO of butadiene, LUMO of ethylene.

Figure 1.5-1.8 are the frontier orbitals of the transition state for the Diels-Alder reaction between butadiene and ethylene produced by the combination of the 4 molecular orbitals shown in Figure 1.1-1.4.

Figure 1.5 is the interaction between HOMO of butadiene and LUMO of ethylene, which is an asymmetric-asymmetric interaction.

Fig 1.5 HOMO-1 of TS

Figure 1.6-1.7 are the HOMO and LUMO of the transition state of this reaction. By comparing these orbitals to the ones shown in figure 1.1-1.4, this interactions are between the LUMO of butadiene and HOMO of ethylene, which are symmetric-symmetric interaction. The two molecular orbitals are bonding and anti-bonding orbital pairs.

Fig 1.6 HOMO of TS

Fig 1.7 LUMO of TS

Figure 1.8 is the interaction between LUMO of ethylene and another molecular orbital of butadiene.

Fig 1.8 LUMO+1 of TS

Results shows that orbitals must have same symmetries to interact. Symmetric-symmetric and asymmetric-asymmetric interactions are allowed as shown in figure 1.5-1.7 (orbital of butadiene is not shown individually, so it cannot act as a support to the observation yet). Phases of the molecular orbitals match when they have same symmetries, leading to non-zero orbital overlap integrals for these orbital interactions. Yet, no interaction between HOMO of butadiene and HOMO of ethylene, or LUMO of butadiene and LUMO of ethylene are observed because they are symmetric-asymmetric interactions. When symmetries of the orbitals are different, phases of orbitals mismatch, causing no overlap possible.

Bond Lengths

According to literature, typical C-C single and double bonds are around 1.54 and 1.34 Å respectively . The Van de Waals Radius of Carbon was reported to be 1.70 Å. Optimization of butadiene shows that the C-C single and double bonds are 1.5400 and 1.3552 Å respectively. With good agreement to literature values, butadiene shows two terminal C-C double bond and a C-C single bond in between. In the transition state of this cycloaddition, the C-C bond length becomes 1.3907, 1.3968, and 1.3962 Å. The three C-C bonds have similar bond lengths, all between the typical bond length of C-C single and double bonds. This indicates that in the transition state, C-C double bonds are weaken and C-C single bond is strengthen, because the electron density are delocalized among the carbon atoms.

Vibrations

Figure 1.9 and 1.10 show the vibrational modes of the transition state of the Diels-Alder reaction at the two lowest vibrational frequencies.

Fig 1.9 Vibration at transition state

Fig 1.10 Vibration of lowest positive frequency

The vibration with negative frequency corresponds to the reaction path as it represents the only geometric coordinate with the negative second derivative. Figure 1.9 illustrates the vibration mode at the transition state, showing that the two terminal carbons of the butadiene and the carbons on ethylene stretching towards each other simultaneously. This suggests that the formation of the two bonds is synchronous. In contrast, the vibration of the lowest positive frequency shown in figure 1.10 shows that the molecules are rotating on two parallel planes. In each of the oscillations, terminal carbon atoms align with ethylene carbon atom twice. However, this vibration shows no displacement of the molecules towards each other.

Nf710 (talk) 23:24, 15 December 2016 (UTC) Good First Section however you didnt put an MO diagram in.

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Reaction between cyclohexadiene and 1,3-dioxole is another Diels-Alder reaction. Unlike ethylene, 1,3-dioxole is not a linear molecule, leading to two possible arrangements in its reaction with cyclohexadiene, and hence two possible products—endo and exo adduct. This exercise aims to show which product is preferred.

Molecular orbitals of Transition states

In this reaction, the dienophile involved has two ether group adjacent to the alkene. The ethers act as an electron donating group, raising the electron density of the alkene. This changes the electron demand in this Diels-Alder reaction. In normal electron demand, diene is the electron rich species that donates electron density to electron poor dienophile. The interacting frontier orbitals in this case are HOMO of diene and LUMO of dienophile, which is an asymmetric-asymmetric interaction, resulting in asymmetric HOMO in the transition state. Yet, when electron demand changes. This is referred as the inverse electron demand Diels-Alder reaction. As dienophile is more electron rich, its energy increases. The orbitals with the closest energies become the LUMO of diene and HOMO of dienophile. This orbital interaction is a symmetric-symmetric interaction, resulting in a symmetric HOMO in the transition state. In short, when the HOMO of the transition state is symmetric, it indicates that the reaction is an inverse electron demand Diels-Alder reaction.

Fig 2.1 HOMO of Endo Transition State

Fig 2.2 LUMO of Endo Transition State

Fig 2.3 HOMO of Exo Transition State

Fig 2.4 LUMO of Exo Transition State

(These are the products, no the TS. When you reoptimise a TS you must still use opt=(ts,calcfc) Tam10 (talk) 16:14, 6 December 2016 (UTC))

As shown in figure 2.1 and 2.3, the HOMO of both endo and exo transition states are the bonding orbital of cyclohexadiene and 1,3-dioxole. This symmetrical orbital interaction is a result of a symmetric-symmetric interaction between the reactants. The LUMO of these transition states are results of a asymmetric-asymmetric interaction instead, involving the LUMO of cyclohexadiene interacting with 1,3-dioxole. As this reaction involves 1,3-dioxole as the electron rich dienophile and cyclohexadiene as the electron poor diene, the HOMO of both endo and exo transition states are symmetrical, indicating that this is an inverse demand Diels-Alder reaction.

Energies

As Diels-Alder reaction is irreversible, kinetic product is the preferred product, which can be predicted by computing the activation energies for the two product formations. The transition state with the lower energy would be preferred, so the product of that pathway is the major product. Kinetic product is the product that requires the smallest activation energy, which is the energy required to overcome the energy difference between the energy of reactants and that of the transition state. In contrast, thermodynamic product is the product that has the lowest energy, which also means the reaction has the largest change in enthalpy. The table below shows a summary of the activation energy and enthalpy change of the endo and exo product formation pathways.

Table 1: Gibbs free energies (kJ/mol) (Exercise 2)

	Cyclohexadiene	1,3-Dioxole	Transition state	Activation energy	Adduct energy	Overall change in Gibbs free energy
Endo	0.116876	-0.05228	0.137942	0.073341	0.037806	-0.02679
Exo			0.138904	0.074308	0.037974	-0.02662

(These are PM6 energies not B3LYP Tam10 (talk) 16:14, 6 December 2016 (UTC))

As shown in the table, at room temperature, formation of endo adduct has a smaller activation barrier than exo adduct as it requires a smaller activation energy. However, the exo adduct is lower in energy than endo adduct, resulting in a greater enthalpy change and greater stability. In short, the endo product is the kinetically favourable product, while the exo product is the thermodynamically favourable product. Since Diels Alder reaction forms kinetic product preferably, endo adduct is the major product of this reaction.

Secondary orbital interactions

Figure 2.1 shows that there is strong secondary orbital interaction between the oxygens and the carbons where double bond is formed in the product in the HOMO of endo transition state. In contrast, figure 2.3 shows no interaction is observed between oxygen and any other atoms in the HOMO of exo transition state, only dispersed overlapping between the hydrogens is shown. The presence of strong secondary orbital overlap stabilizes the energy of the endo transition state, resulting in a lower activation barrier comparing to the exo adduct formation. This explains why endo is the kinetically preferred product in Diels-Alder reaction.

Nf710 (talk) 23:34, 15 December 2016 (UTC) This section was done well, you used the wrong level of theory though, B3LYP is far more superior. but you still came to the correct conclusions.

Exercise 3: Diels-Alder vs Cheletropic

This exercise is about the reaction between o-xylylene and SO₂. With the terminal o-xylylene carbons acting as the cis-diene and SO₂ as the dienophile, the two reactants can perform Diels-Alder reaction, forming endo and exo adducts. Meanwhile, cheletropic reaction can happen to form 1,3-dihydrobenzo[c]thiophene-2,2-dioxide. (Cheletropic reaction is another type of cycloaddition where two sigma bonds are formed between a single atom and two terminal atoms of a conjugated system .) The difference between the two types of reactions will be explored in this exercise.

Adduct structures, Transition state structures and IRC paths

The three possible adducts and their corresponding transition states are optimized at PM6 level as shown below, along with their calculated IRC paths:

Fig 3.1 Endo Diels-Alder reaction adduct	Fig 3.2 Exo Diels-Alder reaction adduct	Fig 3.3 Cheletropic reaction adduct
Fig 3.4 Cheletropic reaction adduct	Fig 3.5 Exo Diels-Alder reaction transition state	Fig 3.6 Cheletropic reaction transition state
Figure 3.7 IRC path of Endo Diels-Alder reaction pathway.	Figure 3.8 IRC path of Exo Diels-Alder reaction pathway.	Figure 3.9 IRC path of Cheletropic reaction pathway.

(Be careful when reusing code that you change the titles too Tam10 (talk) 16:14, 6 December 2016 (UTC))

Energies

Table 2: Gibbs free energies at room temperature (kJ/mol) (Exercise 3)

	O-xylylene	SO2	Transition state	Activation energy	Adduct	Overall change in Gibbs free energy
Endo	0.178991	-0.11861	0.090558	0.030181	0.067965	0.007588
Exo			0.092076	0.031699	0.021451	-0.038930
Cheletropic			0.099062	0.038685	-0.000005	-0.060380

(The endo adduct energy appears to be incorrect. I think you took the energy from the "sum of electronic and thermal enthalpies" Tam10 (talk) 16:14, 6 December 2016 (UTC)) (These energies are not in kJ/mol! You need to multiply by 2625.5 kJ mol^-1Hartree^-1 Tam10 (talk) 16:14, 6 December 2016 (UTC))

Figure 3.10 Reaction profile of endo and exo Diels-Alder and cheletropic reaction between o-Xylylene-SO₂.

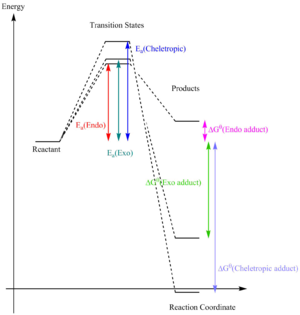
Figure 3.10 shows the relative energies of the reactant, transition states and product in each Diels-Alder and cheletropic reaction. it is shown that the activation barrier of the cheletropic reaction is the highest among the three reaction pathways——0.038685 kJ/mol, meaning it is kinetically least favourable product. Yet, it is at the same time the thermodynamically most favourable product because it has the most negative enthalpy change of -0.06038 kJ/mol. On the other hand, the endo product of the Diels-Alder reaction has the smallest activation barrier but a positive enthalpy change, meaning it is the kinetically most favourable product but thermodynamically least favourable. therefore, the most kinetically preferred product is the endo product in the Diels-Alder reaction, while the most thermodynamically preferred product is the cheletropic reaction product.

Another possible reaction site

O-xylylene has another cis-butadiene fragment which can act as another diene for the Diels-Alder reaction as well. However, the reaction at this diene was neglected in the previous analysis because it is found that the reaction at this reaction site are thermodynamically and kinetically unfavourable. The unfavourable adducts are shown in figure 3.11 and 3.12.

Fig 3.11 Diels-Alder endo product at unreactive diene of o-xylylene

Fig 3.12 Diels-Alder exo product at unreactive diene of o-xylylene

Table 3: Gibbs free energies at room temperature (kJ/mol) (Exercise 3-Extra)

	O-xylylene	SO2	Transition state	Activation energy	Adduct	Overall change in Gibbs free energy
Endo	0.178991	-0.11861	0.102070	0.041689	0.065610	0.005229
Exo			0.105054	0.044673	0.0067304	0.006923

By comparing the activation energies and adduct energies in table 2 and 3, it is obvious that the activation barriers of the reactions at the diene in the ring are much higher than that at the terminal dienes. This means these reactions have require high energies to proceed. Also, both of the reactions with the diene in the ring result in positive change in Gibbs free energy, indicating none of this reactions are spontaneous. The reaction site causes a huge difference in the change energies of the products because when SO₂ reacts with the terminal diene, an aromatic system is formed in the 6-memberd ring of the o-xylylene (refer to figure 3.1 and 3.2). The formation of this aromatic system allow the transition states and the product to gain high stability, hence lowering the transition state and adduct energies. Therefore, the reaction at the terminal dienes of the o-xylylene is preferred over the reaction at the cis-diene in the ring.

Conclusion

Although transition state cannot be isolated in reality, computation on the PES of a reaction allows the analysis on the transition states and the IRC. Knowing the energy level and frontier molecular orbitals of the transition state provide information about the activation barrier of different reaction modes in Diels-Alder reaction. This is rationalized by assessing sterics effect on the formation of products and visualizing the secondary orbital interactions involvement. Combining all the information allows the determination of the most kinetically and thermodynamically favoured reaction path.

Reference

<references>