Rep:SJP115 Transition States And Reactivity By Sarah Patterson
Introduction
Potential Energy Surface
Potential energy surfaces depict the energy of a molecule as a function of its geometry across all dimensions. A non-linear molecule will have 3N degrees of freedom in three dimensional space. The degrees of freedom may be decomposed into translational, rotational and vibrational motion. The rotational and translational motions do not vary the internuclear distances of the molecule and will not affect its potential energy. This means an N-atom molecule will have 3N-6 degrees of freedom remaining, and this leads to a PES with 3N-6 geometric variables. A key approximation made upon generating a PES is that the Born-Oppenheimer approximation is valid and that the energy can be given as a function of the positions of the nuclei.
The potential energy landscape will contain stationary points, at such points the first derivative of the potential energy with respect to each geometric parameter (equivalent to the gradient) will be zero (eq 1.).
 |
|---|
This can be related to the force acting on the atoms. In one dimension this force will have a single value; in three dimensions the force will be the first derivative matrix (the gradient matrix), and the force constant will be the second derivative matrix, the Hessian matrix. Normal modes are the eigenvectors of this Hessian matrix. [2] Matrices provide an advantage over linear algebra, since they allow the Hamiltonian to be easily diagonalised and the eigenvectors and eigenvalues solved.
A stationary point may correspond to a minimum or saddle point transition structure. They are distinguished by the curvature surrounding the stationary point. The curvature of each dimension can be found by computing the force constant Hessian matrix eigenvalues for each normal mode (second derivative). At a minimum the second derivative will be positive in all dimensions and there are no negative force constants. Movement along any degree of freedom will raise the energy hence a minimum represents a stable or quasi configuration of a molecule. If the vibrational frequencies are real, then this confirms the structure is a minimum.
 |
|---|
A TS will have a single negative hessian eigenvalue and this unique normal coordinate corresponds to the reaction coordinate. In other words, a transition state (TS) is a maximum along a minimum energy path connecting two minima. The single negative hessian eigenvalue will lead to an imaginary frequency vibration which is indicative of the TS. The vibrational mode of the imaginary frequency should match the action of the reaction path. If there is more than one imaginary frequency, there will be a lower energy pathway connecting the minima.
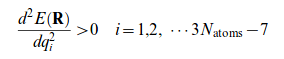 |
|---|
 |
|---|
TS control reactivity since they are the highest energy point that must be overcome to go from reactant to products. In this experiment, Gaussian was used to locate the TS of a number of pericyclic reactions based on the local shape of the potential energy surface.
Nf710 (talk) 12:27, 16 April 2018 (BST) Excellent understanding of how we manipulate the properties of the PES to obtain chemical properties.
Computational Methods
Two electronic structure methods in Gaussian were used to solve the Schrödinger equation and generate the potential energy landscape for the reactions.
Method 1: The first method employed was the semi empirical quantum chemical PM6 (Parameterization Method 6) method which is based on the Hartree Fock Hamiltontian. Approximations are made in order to solve the Hamiltonitan matrix which consist of using experimental data. Parameterised corrections are also made to correct for the approximate quantum mechanical model.[3] The PM6 method fails in accounting for non-covalent interactions such as the dispersion energy and hydrogen bonding. The vast number of approximations and use of experimental data makes this method less accurate. Nonetheless, this semi-empirical calculation remains much faster than its ab initio counterpart, allowing the system to be modeled in a reasonable amount of time.
Method 2: The B3YLP method is a hybrid method between Density Functional Theory (DFT) and the Hartree Fock theorem. The electronic wavefunction is given by the basis set 6-31(d) [4]. Both of the hybrid methods are used to recover electron correlation. The Hartree Fock method accounts for the exchange correlation. The DFT method recovers the dynamic electron correlation and solves the DFT hamiltonian.
In this experiment PM6 was used as the primary calculation method. Exercise 1 and 2 were carried out solely using PM6, whereas in exercise 3 the PM6 results were further optimised using the B3YLP method.
The Hartree Fock approximation
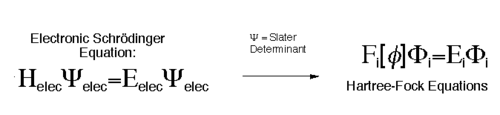
The Hartree Fock (HF) approximation is central to finding solutions to the Schroginger equation by overcoming the many-electron problem. In order to describe the wavefunction of the ground state of an N-electron system, a Slater determinant is used. [5] According to the variational principle the best wavefunction will be the one with the lowest energy. The energy can be lowered by changing the spin orbitals. [6]This leads to the Hartree Fock equation, as seen in equation 5.
 |
|---|
The Hartree Fock approximation overcomes the complicated, many electron problem, by treating it as a one-electron problem and accounting for electron-electron repulsion in an average way. [8] The Hartree Fock equation can then be solved using the self-consistent field (SCF) method. This method involves making an initial guess for the spin orbitals, calculating the average electron field, and solving the HF equation to obtain a new set of spin orbitals. This process is then repeated with the new set of spin orbitals until the basis sets lower the Hartree Fock energy to a limit called the Hartree Fock limit. [9]
Nf710 (talk) 12:37, 16 April 2018 (BST) This is a very good understanding of the quantum mechanical methods. You could have expanded the fock operator to show what the terms contain. There is a very good introduction to this in the book by Szabo and Ostlund if you are interested.
Methods for Locating and Characterising Transition States
There are three different methods for localising and characterising transition states:
Method 1: The structure of the transition state is estimated and a PM6 TS calculation is carried out. If successful the optimised transition state should have a single imaginary frequency and a successful IRC path with a gradient of zero at the TS. Further optimisation can then be carried out using a B3LYP/6-31g(d) calculation. Whilst this is the fastest method, it suffers from various drawbacks; it requires prior knowledge of the transition state and failure to adequately estimate the structure will result in a failed calculation or the wrong TS structure.
Method 2: Similarly to method 1, the initial step of method 2 is to estimate the structure of the transition state. However, the atom pairs involved in the bond forming reaction are frozen in space preceding optimisation to a minimum. This enables the rest of the structure to be optimised and the TS can then be calculated using PM6 (and B3LYP/6-31g(d)). The primary disadvantage of method 2 is that it requires knowledge of the TS, but it provides a more significant means of locating the TS compared to method 1.
Method 3: This is the most infallible method of locating the TS as it does not require knowledge of the TS. The downside of the method is that it is slow, requiring many steps. In addition difficulties can arise if the TS is located far from the reactant and product minima. In this method either the reactant or product geometries are optimised, and the bond lengths are then modified to resemble the TS. The atom pairs involved in the reaction are then frozen, and from the optimised structure a TS calculation can be carried out.
Method 2 was used for exercise 1 and 2. Exercise 3 was carried out using method 3.
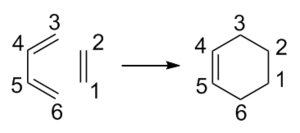
Exercise 1: Reaction of Butadiene with Ethylene
(Fv611 (talk) Excellent work across the whole exercise - very well done!)
 |
|---|
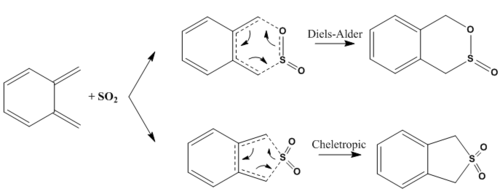
The conjugated butadiene undergoes a thermal [4+2] cycloaddition with ethene to form an unsaturated six-membered ring. There are 6 electrons moving in suprafacial fashion making the reaction pericyclic. The absence of substitution on the fragments avoids issues of stereoselectivity.
Molecular Orbital Analysis
Analysis of the molecular orbitals of ethene and butadiene enables the determination of how the orbitals interact to form the transition state. In a product molecular orbital diagram the reactants overlap to form bonding and anti-bonding MOs which are stabilised and destabilised more than the reactants respectively. Whilst a transition state MO diagram also shows stabilising and destabilising interactions, the orbitals remain raised in energy. This can be rationalised by the definition of a transition state as the maximum on the minimum energy path or a stationary point with a single negative Hessian eigenvalue. There is an activation barrier that must be surmounted to reach the transition state.
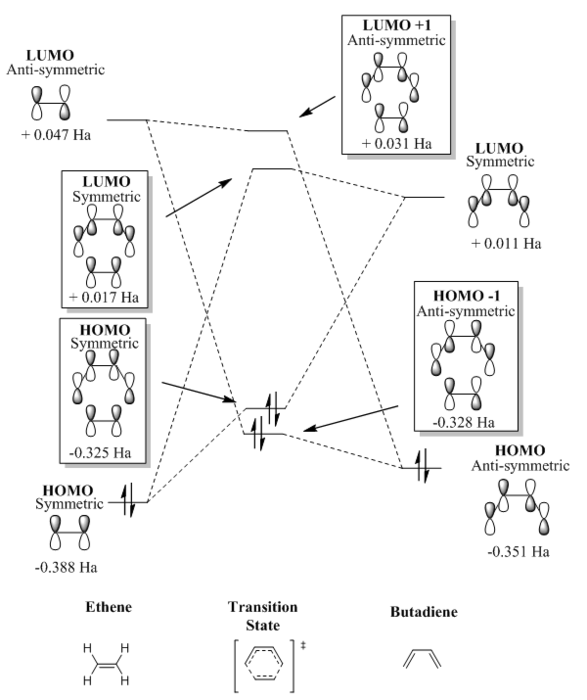
From the visualisation of the MOs in table 1 it can be seen that HOMO-1 is formed from a stabilising interaction between the HOMO of butadiene and the LUMO of ethene. Similarly, the HOMO TS is formed from the stabilising overlap of the HOMO of ethene and the LUMO of butadiene. The LUMO of the transition state is formed from a destabilising interaction between the overlap of the LUMO of butadiene with the HOMO of ethene. The destabilising overlap of the HOMO of butadiene and the LUMO of ethene affords the LUMO+1. The interaction between the orbitals is consistent with the observations made by Fukui et al. [10] ; the occupied orbitals of different molecules do not interact whilst the the occupied orbitals of one molecule and the unoccupied orbital of another will interact with each other causing attraction. Moreover, it can be deduced that interacting orbitals must be of the same symmetry. The symmetric HOMO of ethene and the symmetric LUMO of butadiene overlap to give a symmetric HOMO and LUMO whilst the antisymmetric HOMO of butadiene and the anti-symmetric LUMO of ethene give the anti-symmetric HOMO-1 and LUMO+1. The orbitals must be of the same symmetry in order to interact, and the overlap integral is a measure of their interaction. Orbitals of the same symmetry will interact strongly and have a non-zero value of the overlap integral. In a forbidden reaction such as that with an anti-symmetric and symmetric orbital combination, the overlap integral will be zero and there will be no interaction between the orbitals. The symmetry of the orbitals can be determined by a plane of symmetry passing vertically through the orbitals.
The Diels Alder reaction undergoes normal electron demand. The reactivity is controlled by the relative energies between the Frontier Molecular orbitals where the key interaction will be between the HOMO and LUMO that are closer in energy. From figure 2 it can be seen that the smallest energy gap will be between the HOMO of butadiene and the LUMO of ethene. The smaller energy gap will result in a better overlap in the transition state. The energies in the molecular orbital diagram (figure 2) were obtained by doing a single point energy calculation on the reactants obtained from the IRC. The TS energies were equally obtained by doing a single point energy calculation of the TS. Using these energies it can be seen quantitatively that the energy gap between the HOMO of butadiene and the LUMO of ethene is 0.398 Ha, whilst the energy gap between the HOMO of ethene and the LUMO of butadiene is 0.399 Ha. Although there is a small energy difference, the reaction is still expected to proceed via a normal electron demand Diels Alder.
 |
|---|
The molecular orbital diagram for the transition state (figure 2) was constructed using the molecular orbitals in table 1.
| Visulisation of the Reactant Molecular Orbitals | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ethene HOMO | Ethene LUMO | Butadiene HOMO | Butadiene LUMO | ||||||||
| Visualisation Transition State Molecular Orbitals | |||||||||||
| Transition State HOMO -1 | Transition State HOMO | Transition State LUMO | Transition State LUMO +1 | ||||||||
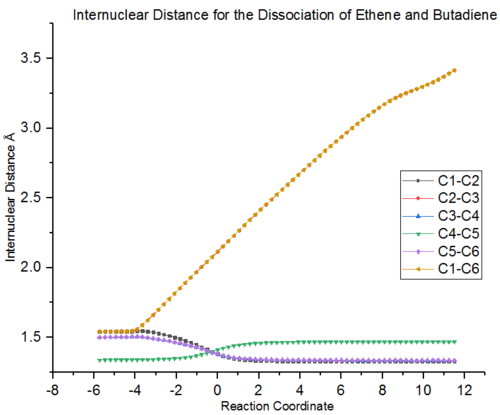
Bond Distance Changes
Table 2 illustrates the changes in bond length that occur throughout the reaction with two π bonds being broken and concomitant formation of two single bonds. Examination of the C1-C2 ethene double bond shows a clear elongation upon formation of the transition state and subsequent lengthening in the product to form a single bond. The change in bond length is consistent with the change in hybridisation from sp2 to sp3 for both C1 and C2 that occurs throughout the course of the Diels Alder reaction. The two double bonds of the butadiene fragment, C3-C4 and C5-C6, are equally progressively lengthened from double to single bonds. In this case C4 and C5 remain sp2 hybridised whilst C3 and C6 change hybridisation state from sp2 to sp3. The internal single bond of the butadiene fragment is shortened in the transition state to form a double bond in the product. Typical values for the interatomic distance between a carbon-carbon sp3 single bond is 1.54 Å whilst that for a carbon-carbon sp2 double bond is 1.34 Å [11]. The literature values closely match the single and double bond lengths in the product. However, butadiene's internal single bond (C4-C5) appears slightly shorter than is expected for a single bond and this is a result of it being a conjugated diene with π electrons delocalised across the fragment. Similarly in cyclohexene the bonds adjacent from the double bond (C3-C4 and C5-C6) are slightly shorter than a typical single bond and this is a result of adjacent carbon being sp2 hybridised thus benefiting from additional s character. The C2-C3 and C1-C6 interatomic distances represent the bonds that are formed between ethene and butadiene to form single bonds in the cyclohexene product. In the TS these bond lengths appear as approximately 2.115 Å, this is shorter than twice the Van der Waals radius of carbon which is indicative of interaction between the electron densities of the two carbon atoms [12].
| Bond Length (Å) | ||||
|---|---|---|---|---|
| Carbon-Carbon Bond | Ethene | Butadiene | Transition State | Cyclohexene |
| C1-C2 | 1.3273 | n/a | 1.3818 | 1.5345 |
| C2-C3 | n/a | n/a | 2.1147 | 1.5372 |
| C3-C4 | n/a | 1.3352 | 1.3798 | 1.5008 |
| C4-C5 | n/a | 1.4683 | 1.4111 | 1.3370 |
| C5-C6 | n/a | 1.3352 | 1.3798 | 1.5008 |
| C6-C1 | n/a | n/a | 2.1149 | 1.5372 |
The changes in bond length during the course of the reaction are further illustrated by figure 3. The reaction coordinate shows the dissociation of the cyclohexene product into the ethene and butadiene reactants. The double bond in cyclohexene (C4-C5) is lengthened from a single to double bond. The neighbouring single bonds (C3-C4 and C5-C6) are shorthened to double bonds. C1-C2 is shorthened to reform the ethene double bond. The bond distances C2-C3 and C1-C6 show the single bonds between the two fragments being lengthened and the bonds being broken.
 |
|---|
Reaction Path Vibrations
The animation below shows the vibrational mode of the imaginary frequency of the TS which occurs at 948.5i cm-1. This vibrational mode matches the action of the reaction path. The animation shows that the reaction is both synchronous and concerted with two new bonds forming simultaneously. Table 2 provides further evidence for a synchronous reaction path since the two forming bonds have the same length.
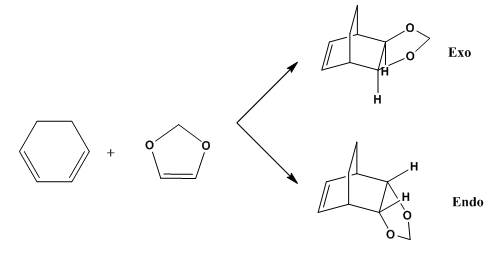
Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole
 |
|---|
The Diels-Alder between cyclohexadiene and 1,3-dioxane can proceed in an exo and endo manner. The different pathways rely on the approach of the 1,3-dioxole towards the cyclohexadiene. If the dioxole approaches the diene with the oxygen atoms lying beneath the ring then the endo product will result. Conversely, if the dioxole ring oxygens point away from the diene, the exo product will predominate.
Molecular Orbital Analysis
(Fv611 (talk) Very nice MO diagrams.)
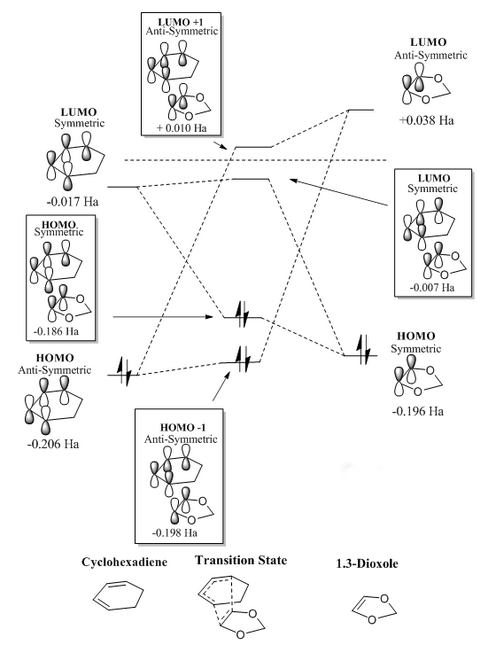
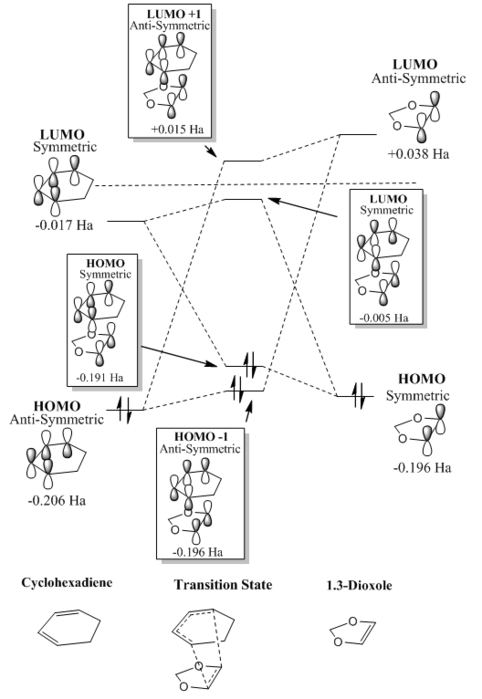
MO diagrams were constructed for both the exo and endo transition states, these can be seen in figure 5 and 6 respectively. The MO diagrams show the same observation as made in exercise 1; orbitals can only overlap if they are of the same symmetry. The anti-symmetric diene HOMO and dienophile LUMO generate the anti-symmetric TS HOMO-1 and LUMO+1. The symmetric HOMO dienophile and LUMO diene afford the symmetric HOMO and LUMO.
 |
 |
|---|
A normal electron demand Diels Alder reaction typically proceeds between an electron rich diene and an electron poor dienophile. The smallest energy gap controls the reactivity and for a normal electron demand Diels Alder reaction this will be between the HOMO of the diene and the LUMO of the dienophile. The small energy gap will enable strong overlap between the orbitals. Inverse electron demand Diels Alder reactions are typical of an electron poor diene, with an electron withdrawing group that lowers the energy of the HOMO and LUMO, and an electron rich dienophile, with electron donating groups that raise the energy of the HOMO and LUMO. The HOMO of the dienophile will lie above the diene’s HOMO and the smallest energy gap will be between the HOMO of the dienophile and the LUMO of the diene. The energy gap between the HOMO and LUMO frontier molecular orbitals in both normal and inverse electron demand can be seen in figure 7.
 |
|---|
From the MO diagrams (figure 5 and 6) it can be seen that both the endo and exo reactions undergo inverse electron demand Diels Alder. There is a smaller energy gap between the 1,3-dioxole HOMO and the cyclohexadiene LUMO than the 1,3-dioxole LUMO and cyclohexadiene HOMO. The 1,3-dioxole has two electron donating oxygen substituents which raise the energy of the HOMO and LUMO, such that the HOMO of the dienophile is higher in energy than the cyclohexadiene HOMO. The HOMO of the dienophile will hence interact more strongly with the LUMO cyclohexadiene. The energies reported in the MO diagrams are those from the B3YLP optimisations of the reactants and the transition state. In order to quantify the energy gap between the HOMO and LUMOs of the two reactants, a single point energy calculation was carried out from the IRC for both the endo and exo reactants. The results are summarised in table 3.
| Endo | Ha | Exo | Ha |
|---|---|---|---|
| 1,3 Dioxole HOMO | -0.317 | 1,3 Dioxole HOMO | -0.322 |
| 1,3 Dioxole LUMO | 0.032 | 1,3 Dioxole LUMO | 0.030 |
| 1,3 Cyclohexadiene HOMO | -0.321 | 1,3 Cyclohexadiene HOMO | -0.322 |
| 1,3 Cyclohexadiene LUMO | 0.023 | 1,3 Cyclohexadiene LUMO | 0.021 |
From table 3 it can be seen that the energy gap between the cyclohexadiene LUMO and 1,3 dioxole HOMO is approximately 0.34 Ha whilst the energy gap between the cyclohexadiene HOMO and 1,3 dioxole LUMO is approximately 0.35 Ha. This provides further, quantitative evidence for an inverse electron demand Diels Alder.
| Visualisation of the Exo Transition State Molecular Orbitals | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Transition State HOMO-1 | Transition State HOMO | Transition State LUMO | Transition State LUMO+1 | ||||||||
| Visualisation of the Endo Transition State Molecular Orbitals | |||||||||||
| Transition State HOMO -1 | Transition State HOMO | Transition State LUMO | Transition State LUMO +1 | ||||||||
Thermochemistry
Under the thermochemistry section of the log file, the “sum of electronic and thermal free energies” was extracted for the reactants, TS and the product. The activation energy was then was computed by doing the energy difference between the TS and the reactants. The reaction energies were calculated by calculating the energy difference between the product and the reactants. The results are summarised in table 5.
| Reaction Type | Energy (kJ/mol) | ||||||
|---|---|---|---|---|---|---|---|
| Reactants | Transition State | Product | Activation Energy | Reaction Energy | |||
| Diene | Dienophile | Total | |||||
| Exo | -612593.146 | -701188.7353 | -1313781.88 | -1313614.23 | -1313845.68 | 167.65 | -63.80 |
| Endo | -1313622.07 | -1313849.27 | 159.23 | -67.39 | |||
Examination of the activation energies in table 5 shows that there is a larger activation barrier to reach the exo TS than the endo TS. The endo TS is thus more stable than the exo TS. In order to reach the exo TS, the reactants will require additional energy to surmount the larger activation barrier. The fastest formed, kinetically favoured product, with the lower activation barrier will hence be the endo product.
The reaction energies show that whilst both the endo and exo reactions are exothermic and thermodynamically favourable, the endo product is lower in energy and thermodynamically more stable than the exo. The reaction energy for the endo is more negative, more exothermic and presents the thermodynamically most stable product. The endo product is thus not only kinetically favoured but also thermodynamically favoured. The exo product is higher in energy as a result of the steric clash between the bridging carbons and the 5 membered dioxole ring.
Secondary Orbital Interactions
The lower energy of the endo TS can be rationalised on the basis of secondary, non-bonding, interactions between the dioxole oxygen p orbitals and the π system of the diene. Such interactions lower the energy of the TS HOMO promoting faster formation of the kinetic product. The exo TS only has primary orbital interactions and this is a result of the oxygen p orbitals of the dioxole pointing away from the diene p orbtials making them too far apart to interact. The HOMO of both the exo and endo TS are given in table 5 wherein the isovalue has been set to 0.01, this has the effect of shortening the radial extension of the orbitals making the stabilising interactions of the endo clearer.
| Exo Secondary Orbital Interactions | Endo Secondary Orbital Interactions | ||||
|---|---|---|---|---|---|
In the exo TS HOMO the p orbitals of the dioxole do not interact with the diene p orbitals, whereas in the endo TS HOMO the p orbitals of the dioxole do interact with those of the diene.
Nf710 (talk) 12:42, 16 April 2018 (BST) Excellnnet section. Your analysis of the electron demand was excellent and you have got the correct energies. And your conclusions from these results are correct. Well done.
Exercise 3: Diels-Alder vs Cheletropic
 |
|---|
The reaction scheme shows the potential pathways for the reaction between o-xylyene and sulphur dioxide. The Diels-Alder reaction can proceed in an endo or exo fashion. The cheletropic reaction is characterised by two σ bonds forming in concert at a single atom. [14]
Intrinsic Reaction Coordinate (IRC)
The IRC for the exo/endo Diels Alder pathways and the Cheletropic reaction are shown in figure 9, 10, 11 respectively. The IRCs show the progression of the reaction, from the SO2 and o-xylyene fragments, to the TS, and finally to the products.
 |
 |
 |
|---|
The exo and endo reactions show asynchronous bond formation, with the bonds forming at different times due to asymmetry. For both Diels Alder reactions the C-O bond between the diene and dienophile are formed before the bond between the diene and sulphur atom (C-S). The cheletropic reaction proceeds with synchronous bond formation; both ends of the diene form new C-S bonds with the sulphur atom of SO2 at the same time. The three reactions all show a fully delocalised 6-membered aromatic ring intermediate and in all three products the six membered ring is aromatic. This illustrates the high instability of xylyene; there is a strong driving force for aromatisation which will drive product formation. Indeed, from the IRCs it can be seen that aromatisation occurs before bond formation.
Thermochemistry
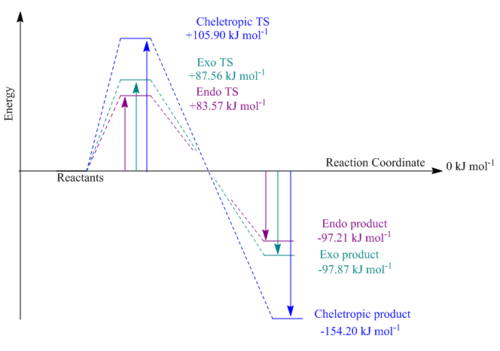
Table 6 was constructed in the same was as in exercise 2, the "sum of the electronic and thermal free energies" were extracted from the log files of the reactants, TS and products and used to calculate the activation and reaction energies. Using the data from table 6 a reaction profile was constructed (figure 12).
| Reaction Type | Energy (kJ/mol) | ||||||
|---|---|---|---|---|---|---|---|
| Reactants | Transition State | Product | Activation Energy | Reaction Energy | |||
| Sulphur Dioxide | Xylyene | Total | |||||
| Exo | -313.14 | 467.33 | 154.19 | 241.75 | 56.32 | 87.56 | -97.87 |
| Endo | 237.76 | 56.98 | 83.57 | -97.21 | |||
| Cheletropic | 260.09 | 0 | 105.9 | -154.2 | |||
The reaction profile clearly illustrates that the endo TS has the lowest energy activation barrier, requiring less energy than the exo or cheletropic to be surmounted. The endo product is hence the kinetic product since it will be formed fastest. The stability of the endo TS could be due to secondary orbital interactions between the p orbitals of the non-bonding oxygen atom of the SO2 dienophile and the π system of the xylene diene. This interaction is not possible for the exo Diels-Alder reaction since the sulphur dioxide approaches the diene with one of its oxygen pointed away from xylyene. The exo TS thus lies slightly higher in energy than the endo. The cheletropic TS has the largest activation energy and this is a result of the ring and angle strain of the 5-membered ring formed. The 6-membered ring in the exo and endo TS are conformationally less strained minimising 1,3 diaxial repulsions and angle strain. The reaction profile highlights that the reactions are all exothermic. The endo and exo products are similar in energy with the endo product being slightly higher in energy. However, the cheletropic product has the lowest reaction energy and it is the thermodynamically favoured product. This can be rationalised by the high bond energy of the two S=O bonds [15].
 |
|---|
An alternative Diels Alder Site
There is an alternative Diels-Alder reaction which can occur at the cis-butadiene fragment in the 6-membered ring of xylyene. This [4+2] cycloaddition can be exo or endo and the IRCs for both pathways are shown in figures 13 and 14 respectively.
|
|
|---|
A thermochemical analysis of these reactions shows that they possess large activation barriers making them less favourable than the previously described Diels-Alder pathways. Not only are these reactions kinetically unfavourable, but they are endothermic with positive reaction energies. The products lie higher in energy than the reactants and require an input of energy to be formed making these reactions thermodynamically unfavourable. This can be accounted for by the absence of aromaticity in the TS or product. Moreover, there is loss of the conjugation between the two butadiene fragments which is present in xylyene. Whilst both pathways are unfavourable, the endo remains more favourable than the exo since it posses a lower activation energy. This could be due to secondary orbital interactions. The reaction energy is also lower for the endo. The endo pathway hence presents both the kinetically and thermodynamically favoured Diels-Alder reaction for this alternative site.
| Reaction Type | Energy (kJ/mol) | ||||||
|---|---|---|---|---|---|---|---|
| Reactants | Transition State | Product | Activation Energy | Reaction Energy | |||
| Sulphur Dioxide | Xylyene | Total | |||||
| Exo | -313.14 | 467.33 | 154.19 | 275.82 | 176.71 | 121.63 | 22.52 |
| Endo | 267.98 | 172.26 | 113.79 | 18.07 | |||
Extension 1: Electrocyclic Ring Closing
Electrocyclic reactions are characterised by the net transformation of a pi bond into a sigma bond. The thermal electrocyclic ring closing of a substituted cyclobutene is a 4nπ electron process which proceeds with conrotatory motion of the groups on the terminal carbons in order to bring the lobes of the orbitals of the same phase together. The stabilising, attractive interaction of bringing two lobes of the same phase together will form a sigma bond.
The reaction path is illustrated by the gif in figure 15.
 |
|---|
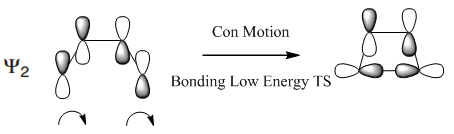
Figure 16 illustrates the effect of conrotatory motion on the orbitals of the HOMO ψ2 for the thermal electrocylcic ring closing.
 |
|---|
(This is where you have to be careful about symmetry. In the products, the orbitals must have rough rotational and reflective symmetry. The product orbitals above have rotational symmetry (symmetric) but an undefined reflective symmetry (antisymmetric at back, symmetric at front). Either the front or the back should rearrange or cancel out to maintain these symmetry requirements. Later in your correlation diagram you show the back as having cancelled out Tam10 (talk) 13:19, 4 April 2018 (BST))
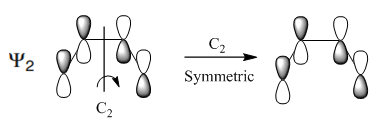
Throughout the rehybridisation reaction the C2 (two-fold) axis of symmetry is maintained. If the phases of the orbitals are preserved under the symmetry transformation they are described as being symmetric.[16]
 |
|---|
A correlation diagram can be constructed to connect molecular orbitals of the same symmetry in the reactants and products (figure 18). This diagram shows that the Ψ2 orbital of butadiene and the sigma orbital of cyclobutene, which are both symmetric with respect to the C2 axis, are correlated. The antisymmetric Ψ1 and π orbitals will be correlated. Similiar considerations apply for the LUMO orbitals in which the antisymmetric sigma star and Ψ3 are correlated. Finally, the Ψ4 and π* will be correlated. The conrotatory process is symmetry-allowed because the bonding orbitals of the reactants correlate with the bonding orbitals of the product with the same symmetry. According to Woodward et al. [17] the highest occupied orbitals dominate these correlations and they can be considered as valence electrons that can be easily perturbed.
 |
|---|
(Show the symmetry axis here for clarity Tam10 (talk) 13:19, 4 April 2018 (BST))
The transition state will have an odd number of phase inversions hence will proceed with a Möbius topology. [18] This TS can be seen in table 8 wherein the π electrons resulting from the 2p atomic orbitals are distributed around a Möbius strip bearing a single half-twist. [19]
| Visulisation of the Reactant Molecular Orbitals | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Butadiene σ | Butadiene π | Butadiene π* | Butadiene σ* | ||||||||
| Visualisation the Product Molecular Orbitals | |||||||||||
| Cyclobutene σ | Cyclobutene π | Cyclobutene π* | Cyclobutene σ* | ||||||||
| Visualisation the Transition State Molecular Orbitals | |||||||||||
| HOMO-1 | HOMO | LUMO | LUMO+1 | ||||||||
The stereochemistry of the reactant and product molecular orbitals provide further evidence for a conrotatory electrocyclic reaction. From the reactant MO in table 8 it can be seen that one of the double bonds is trans whilst the other is cis and following a conrotatory motion the hydrogens originating from the double bond will end up on the same side of the cyclobutene ring.
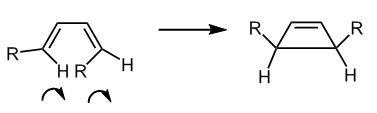 |
|---|
Under photochemical conditions, electronic promotion causes the ψ3 orbital to become the HOMO. The electrocyclic ring closing can only proceed via a disrotatory mechanism and in this case an invariant plane of symmetry will be present. In order to be carry out the photochemical disrotatory electrocyclyic ring closing, Gaussian cannot use single reference calculations. Hartree Fock and density functional theory are not adequate in this case and the multiconfigurational method is required to enable mixing of the various electronically excited states. This method uses a linear combination of configuration states (CSF) to determine the electronic wavefunction. In such calculations the Complete Active Space Multiconfiguration SCF (CAS) is defined to include the approximate spin orbit coupling between the various spin states of the first excited state.
The multiconfigurational method was applied to the substituted butadiene in order to observe the electronic ground state of the photochemical ring closing pathway. The number of electrons and orbitals in the active space were both defined to be four such that the CAS corresponds to the first excited state of butadiene. The output will hence be a minimum on the excited state. Examination of the log file revealed that the excited state is mainly composed of the ground electronic state (1100) and an excited singlet state (a1b0). The geometric configuration of this excited state is twisted making it harder for butadiene to react in this configuration. Although there may be alternative geometric configurations that may react more easily it is envisioned that the disrotatory electrocyclic ring closing will remain more disfavoured than the thermal conrotatory path. This is evidenced by the correlation diagram for the photochemical pathway in which the TS lies higher in energy.
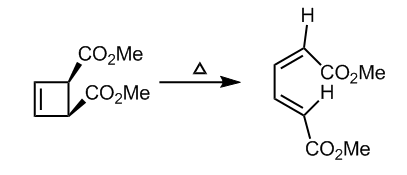
Extension 2: Electrocyclic Ring Opening
 |
|---|
The electrocyclic ring opening reaction illustrated in figure 20 reacts antrafacially according to the Woodward Hoffman rules. This system is also a 4nπ electron system that will proceed with conrotation. The TS shows the intermediate step in the formation of the butadiene double bonds.
 |
|---|
| HOMO of Reactant | HOMO of TS | HOMO of Product | ||||||
|---|---|---|---|---|---|---|---|---|
Conclusion
A number of pericyclic reactions were successfully modeled in Gaussian. PM6 was used as the primary method of carrying out calculations as a compromise between rapidity and accuracy. B3YLP was used when it was necessary to probe reactions with a higher level of accuracy. For example, in exercise 2 the transition state geometries of the exo and endo Diels Alder pathways were elucidated using B3YLP.
Gaussian not only provides a means of locating and characterising transition states, but it also enables the visualization of molecular orbitals. The energies of these molecular orbitals can be used to gain insight into the mechanistic pathway behind the reaction; for example, whether a Diels Alder proceeds via normal or inverse electron demand. The Diels Alder reaction between ethene and butadiene (exercise 1) was found to proceed via a normal electron demand, whilst the Diels Alder between the electron rich 1,3 dioxole and the cyclohexadiene was found to occur via inverse electron demand. Further mechanistic insights can be obtained by animation of the imaginary frequency vibration. This gave an insight into how bond formation occurred, whether bond formation was synchronous or asynchronous. Finally, analysis of the thermochemical data aided in identifying the kinetic and thermodynamic pathways and products.
Files
Reaction of Butadiene with Ethylene
Log file of butadiene and ethene in the same frame PM6
Log file of single point energy of ethene and butadiene
Reaction of Cyclohexadiene and 1,3-Dioxole
Log file of 1,3 Cyclohexadiene B3YLP
Log file of Endo Product B3YLP
Diels-Alder vs Cheletropic
Log file of Cheletropic TS PM6
Log file of Cheletropic IRC PM6
Log file of Cheletopic Product
Log file of Alternative Path Endo TS PM6
Log file of Alternative Path Endo IRC PM6
Log file of Alternative Path Endo Product PM6
Log file of Alternative Path Exo TS PM6
Log file of Alternative Path Exo IRC PM6
Log file of Alternative Path Exo Product PM6
Electrocyclic Ring Closing Reaction
Log file of Electrocyclic Ring Closing Reactants PM6
Log file of Electrocyclic Ring Closing IRC PM6
Log file of Electrocyclic Ring Closing TS PM6
Log file of Electrocyclic Ring Closing Products PM6
Log file of Electrocyclic Ring Closing Reactant HF
Log File of Electrocyclic Ring Closing CAS of first excited state
Electrocyclic Ring Opening Reaction
Log file of Electrocyclic Ring Opening Reactants
Log file of Electrocyclic Ring Opening TS PM6
Log file of Electrocyclic Ring Opening IRC PM6
Log file of Electrocyclic Ring Opening Product
References
- ↑ Joseph J W McDouall Computational Quantum Chemistry: Molecular Structure and Properties in Silico Royal Society of Chemistry 2013 ISBN: 978-1-84973-608-4 http://dx.doi.org/10.1039/9781849737289-00001
- ↑ Joseph J W McDouall Computational Quantum Chemistry: Molecular Structure and Properties in Silico Royal Society of Chemistry 2013 ISBN: 978-1-84973-608-4 http://dx.doi.org/10.1039/9781849737289-00001
- ↑ Jan Reza, Jindrich Fanfrlık, Dennis Salahub, and Pavel Hobza J. Chem. Theory Comput. 2009, 5, 1749–1760
- ↑ J. P. Stewart Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements 2007 DOI: 10.1007/s00894-007-0233-4
- ↑ Attila Szabo, Neil S. Ostlund Modern quantum chemistry: Introduction to Advanced Electronic Structure Theory Dover Books on Chemistry 1989 ISBN: 0486691861
- ↑ Attila Szabo, Neil S. Ostlund Modern quantum chemistry: Introduction to Advanced Electronic Structure Theory Dover Books on Chemistry 1989 ISBN: 0486691861
- ↑ http://www.quimica.urv.es/~bo/MOLMOD/Mike_Colvin/qc/thm.html Last accessed 24th March 2018
- ↑ Attila Szabo, Neil S. Ostlund Modern quantum chemistry: Introduction to Advanced Electronic Structure Theory Dover Books on Chemistry 1989 ISBN: 0486691861
- ↑ Attila Szabo, Neil S. Ostlund Modern quantum chemistry: Introduction to Advanced Electronic Structure Theory Dover Books on Chemistry 1989 ISBN: 0486691861
- ↑ Kenichi Fukui, Teijiro Yonezawa, and Haruo Shingu A Molecular Orbital Theory of Reactivity in Aromatic Hydrocarbons The Journal of Chemical Physics 20, 722 (1952); doi: 10.1063/1.1700523
- ↑ Linus Pauling, and L. O. Brockway Carbon—Carbon Bond Distances. The Electron Diffraction Investigation of Ethane, Propane, Isobutane, Neopentane, Cyclopropane, Cyclopentane, Cyclohexane, Allene, Ethylene, Isobutene, Tetramethylethylene, Mesitylene, and Hexamethylbenzene. Revised Values of Covalent Radii J. Am. Chem. Soc., 1937, 59 (7), pp 1223–1236 DOI: 10.1021/ja01286a021
- ↑ S. S. Batsanov Van der Waals Radii of Elements Inorganic Materials, Vol. 37, No. 9, 2001, pp. 871–885
- ↑ Radleigh A. A. Foster and Michael C. Willis Tandem inverse-electron-demand hetero-/retro-Diels–Alder reactions for aromatic nitrogen heterocycle synthesis Chem. Soc. Rev., 2013, 42, 63-76 DOI: 10.1039/C2CS35316D
- ↑ Angew. Chem. Int. Ed. Engl. 1969, 8, 781–853
- ↑ D. P. Stevenson The Strengths of Chemical Bonds J. Am. Chem. Soc., 1955, 77 (8), pp 2350–2350 DOI: 10.1021/ja01613a116
- ↑ Prof. R. B. Woodward Prof. Roald Hoffmann The Conservation of Orbital Symmetry Angew. Chem. internat. Edit. 1 Vol. 8 (1969) 1 No. II
- ↑ Prof. R. B. Woodward Prof. Roald Hoffmann The Conservation of Orbital Symmetry Angew. Chem. internat. Edit. 1 Vol. 8 (1969) 1 No. II
- ↑ Rainer Herges Topology in Chemistry: Designing Mo1bius Molecules Chem. Rev. 2006, 106, 4820−4842
- ↑ Henry S. Rzepa The Aromaticity of Pericyclic Reaction Transition States Journal of Chemical Education Vol. 84 No. 9 September 2007 •
