Rep:SJ1815 Transition States
Investigating Transition States of Various Pericyclic Reaction
N.B.:Tables in this wiki may extend off the page to the right. Please use the horizontal scrollbar.
Introduction
Transition States: What do we mean?
Transition states are energy maxima along the path of a reaction and the dynamic bottleneck through which a reaction must proceed. Real energy profiles are dependent on multiple variables and you can move the reactants along the energy profile diagram in any direction, so you can encounter many maxima. However, only the one that occurs on your reaction pathway is considered a transition state. To put this in another way, I could take a flask of but-1,3-diene and ethene and expect a Diels-Alder reaction to occur. The transition state would be somewhere where the C-C bonds are being made from the C=Cs in the substrates. I could, given enough energy, stretch one of the C-C bonds to the moon (admittedly, probably breaking it in the process) and you'd have an energy maximum but it wouldn't be a transition state as it isn't part of the reaction in question. Normally for a C-C bond forming process, we take the transition state to be somewhere between the van der Waals radii of the 2 atoms and the C-C bond length.
Locating a transition state
Use Hammond's Postulate
Take a guess at where the Transition State is and optimise using Gaussian. Use Hammond's postulate for where to guess. This is fast, but unreliable, as you have to be a very good guesser.
N.B. Hammond's Postulate: 'The structure of the transition states resembles either the reactants or products (whichever is closest in energy)'[1]
For C-C bond forming reactions, a guess of 2.2 Angstroms for the bond length is a good place to start.
Use the products
A better way of finding a transition state is to optimise the products of a reaction and then remove the bonds formed in the reaction and move the fragments away from each other. Freezing the interacting termini stops the bonds forming while we perform an optimisation to get the lowest energy conformation of the separated fragments. This is then a better guess of the transition state.
Putting it into practice
To actually run the job, use Opt+Freq. This is a geometry optimisation performed via 'solving' the Schrödinger equation, which is ĤΨ=EΨ, and then moving along in small steps of energy, scaled using the second derivative d2E/dq2, where q is the reaction coordinate and frequency calculation using k=d2E/dq2 and 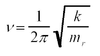 [2]
[2]
As transition states are maxima on a minimum energy surface, they are saddle points overall. This means that while the gradient is zero at this point (the same as for reactants and products), the change in the gradient is negative in one direction only (the direction that links reactant and product wells). As the force constant is related to this change in gradient, it has a negative value in one direction at this transition state too. Due to the fact that frequency is proportional to the square root of the force constant, you get one imaginary frequency in the output file from Gaussian (this is represented as a negative vibration in Gaussview).
Nf710 (talk) 08:26, 23 February 2018 (UTC) This is is correct. But it is better to discuss it in the 3N-6 degrees of freedom of the reaction. This is the basis of the potential energy surface. at te TS geom we can find the force constants by ddiagonalising the hessian matrix. the eigen values are the the force constants and their eigenvectors are the normal modes. the normal modes are there a linear combination of the degreees of freedom and when moving along thwm backwards and forwards it looks like a vibration across the molecules as all the degrees of freedom are changing at once. A TS has 1 negative eigenvalue a minimum has non.
The computer uses variational theorem to run calculations and solve the Schrödinger equation. Variational theorem takes a guess at the wavefunction of a system and then minimises the energy. This means that it hits the potential energy surface after a number of iterations. Depending on where it hits, the optimised .log file can look like a range of different things. A potential energy surface has a lot of local minima- it's 'bumpy'. If the guess wavefunction hits any of these bumps that link two minima together, Gaussview may tell you that it's found a transition state when it hasn't. This is why we need to analyse the results by checking the imaginary vibration and seeing if it matches with our idea of what 'going towards the products' looks like.
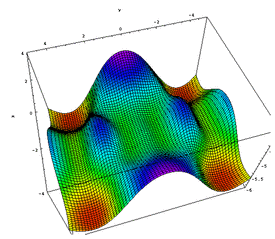 |
| Figure 1: A depiction of a 3D potential energy surface taken from reference 3 [3]. We can only represent energy surfaces in 3D, yet they actually have many more dimensions than this (there are 3N-6 dimensions to consider, where N is the number of atoms in the molecule). |
One approximation to make calculations easier is that we assume that molecular orbitals can be constructed from a linear combination of atomic orbitals. These all have different weightings called orbital coefficients. The wavefunction can therefore be broken down into =ΣNici
As H=E, we then have ΣNmΣNncmHcn
This can be written as a set of matrices with the first being a 1xn matrix of the cn coefficients, then a Hessian matrix of all of the different atomic orbital integrals and then an mx1 matrix of the cm coefficients or, more succinctly, cTHc, where H is the Hessian here. This equals the energy and from this you can get the eigenvalue equation of Hc=Ec, which the computer solves
Nf710 (talk) 08:29, 23 February 2018 (UTC) You are getting confused here. Almost right but the hessian is matrix of second derivatives. This is the Hamiltonian
Each eigenvector of the eigenvalue equation yields 1 molecular orbital.
What are the individual atomic wavefunctions?
These represent electron densityand are best represented by Slater functions.
Slater functions have the form [4]
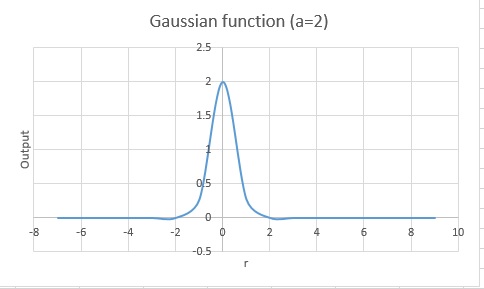
This, however, is too computationally costly to solve, so we use an approximation by using Gaussians.
Gaussian functions have the form An example of thhe form of one of these is shown below.
As these don't represent the orbitals as well as Slater functions, several of them are often summed to better represent these orbitals. This sum adds computational complexity, as there are more integrals to compute, yet this is still faster than using Slater functions. Combining three Gaussians gives a basis set of STO-3G (Slater-Type Orbitals-3 functions Gaussians)[5].
Nf710 (talk) 08:31, 23 February 2018 (UTC) Nice plotting to explain your point. you have clear read beyond the script here. well done.
Optimisation methods
PM6 is a semi-empirical optimisation method. It takes into account the valence electrons for the species and then solves the integrals in relation to them, employing code already on the Gaussian programme [6]. It also uses fixed numbers as approximations for the integrals in the Hessian. This makes it much faster at doing calculations, yet more imprecise in the answers obtained.
B3LYP is a DFT (density functional theory) method, which takes advantage of density fitting (expansion of atomic density rather than computing all of the 2-electron integrals individually)[7]. B3LYP differs from other DFT calculations insofar as it optimises the nuclear wavefunctions, then adds on some electron interactions to see how things change (most DFT calculations just use the nuclei) [8]. However, these are not easily calculated by Gaussian, causing approximations to be formed.
Nf710 (talk) 08:36, 23 February 2018 (UTC) Discussion of PM6 is correct. However some confusion on B3LYP all DFT calculation calculate the one electon and classical 2 electron terms fine. The 2 electron term which comes from the antisymetry of the electron is called the exchange correlation term and this is always unknown in the DFT hamiltonian. This is why you have so many functional which treat this term differently. B3LYP does this by doing a HF calculate and an LDA aprrox.
Tutorial
Tutorial 1- Cope rearrangement of hexa-1,5-diene
The first method for finding a transition state is to guess and then optimise using Opt+Freq, Optimise to a TS (Berny) and calculate the force constants once. There should be 1 negative frequency at the output, which confirms that a transition state has been found and animation of said transition state should make it look like you go from reactants to products. There are 2 different transition states (boat and chair), both of which have been accounted for below
| Boat | Chair | |
|---|---|---|
|
||
| PM6 | File:SJ1815TRIAL COPE TS 2 RADICALS PM6.LOG | File:SJ1815TRIAL COPE TS RADICAL CHAIRTS.LOG |
| B3LYP | File:SJ1815COPEBOATTSB3LYP.LOG | File:SJ1815COPECHAIRTSB3LYP.LOG |
IRC
File:SJ1815 BOAT COPE TS IRC PM6.LOG
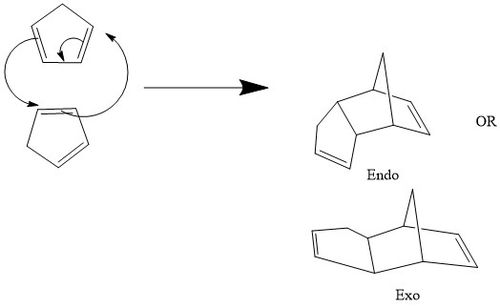
Tutorial 2- Dimerisation of Cyclopentadiene
The second method relies on generating a guess transition state, freezing the atoms in space and then uses method 1 to find exactly where the transition state lies. The keyword opt=modredundant will appear in the submission window, but submit the job as normal, optimising to a minimum. Then, unfreeze the bonds and optimise to a TS, as in method 1. To distinguish between endo and exo conformers, run IRC calculations.
Optimisation:
PM6: File:SJ1815 CYCLOPENTADIENE TRIAL FIXED COORDS OPT+FREQ PM6.LOG
B3LYP:File:SJ1815 CYCLOPENTADIENE TRIAL FIXED COORDS B3LYP.LOG
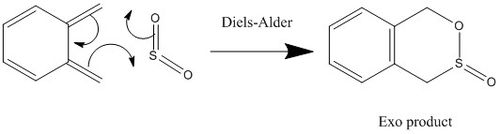
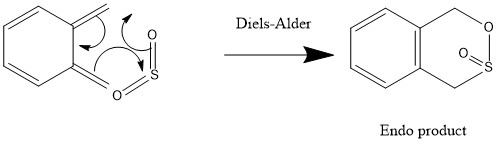
Tutorial 3-Xylylene SO2 Diels-Alder
The third method uses the reactants or products, alters the bond lengths and/or angles (normally of those involved in the reaction, but can be of neighbouring atoms too) and then runs the same way as method 2.
Opt+Freq of Diels-Alder
File:SJ1815 SO2 DIELS-ALDER PM6 MIN.LOG
Exercise 1- Cis-butadiene and ethene Diels-Alder ([4+2]-cycloaddition)
This reaction is often seen as the classic Diels-Alder reaction, due to the fact that the diene and dienophile are as simple as they can be. However, this reaction is purely hypothetical as neither fragment is particularly electron rich or poor (we need this disparity in energies for both normal electron demand and inverse electron demand Diels-Alder reactions).
Optimisation
| Butadiene | Ethene | Cyclohexene | Transition state | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PM6 | File:BUTADIENE SJ1815.LOG | File:SJ1815 ETHENE OPT+FREQ PM6.LOG | File:SJ1815 CYCLOHEXENE PM6.LOG | File:SJ1815 DIELS-ALDER TS10.LOG | ||||||||
| C-C bond Lengths/Å | 1.33343 | 1.32742 | 1.33698 | 1.37977 (original C=C of butadiene) | ||||||||
| 1.47077 | X | 1.50068 | 1.41111 (original C-C of butadiene) | |||||||||
| 1.33343 | X | 1.53703 | 1.37977 (original C=C of butadiene) | |||||||||
| X | X | 1.53491 | 1.38176 (original C=C of ethene) | |||||||||
| X | X | 1.53736 | X | |||||||||
| X | X | 1.50077 | X |
The bond length for a C-C bond is 1.54Å [9] while the C=C bond length is 1.34Å [10] This matches fairly well with the bond lengths in the table above, with the transition state having bond lengths partway between the two lengths. The van der Waals radius of carbon is 1.77Å [11] and all C-C lengths are closer than this, so they are interacting (the van der Waals radius tells us how close atoms have to be for some interaction to take place).
(Fv611 (talk) This bond distance analysis needs a lot more thought. Firs of all, you should have provided Carbon labels to identify the bonds that you are talking about. Additionally, you should have measured the distance between the terminal carbons (the ones which become bonded in the product) at the transition state, to discuss its structure).)
MO analysis
(Fv611 (talk) The discussion of the symmetry requirements could have been expanded upon. Your MO diagram is very nice, but you seem to be confused on which ones are the relevant TS MOs (why are you talking about HOMO-3 but not LUMO+1?). Your MO labelling is inconsistent between the MO diagram and the table.)
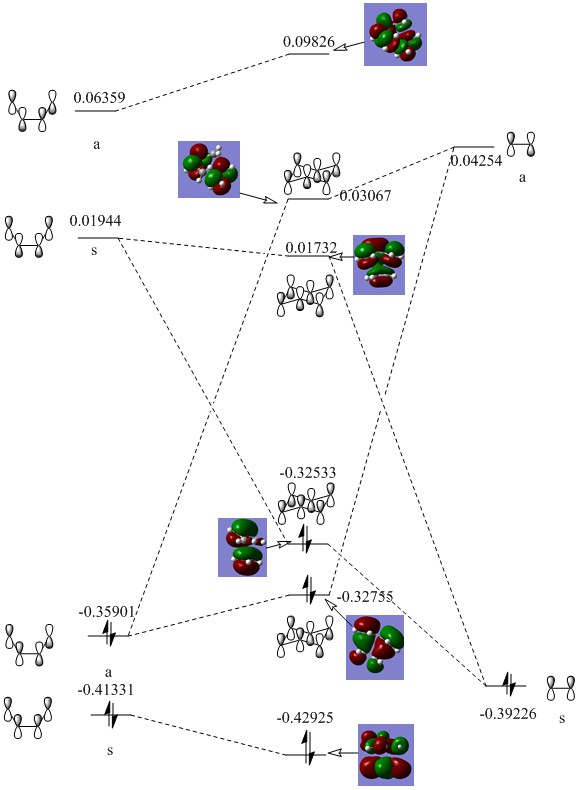
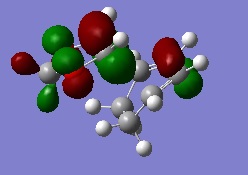
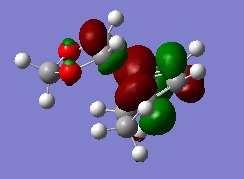
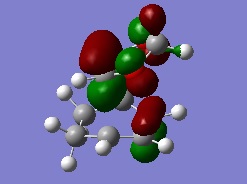
The MO diagram for the reaction is as depicted below
We can see that only orbitals of the same symmetry can interact and have non-zero integrals. This means only fully symmetric or fully antisymmetric combinations are allowed.
The actual, calculated MOs are depicted here:
Depictions of contributing orbitals are portrayed here to help understand where these projected orbitals come from. These have been deconstructed from looking at the calculated MOs.
| MO label | MOs | Corresponding diagram |
|---|---|---|
| LUMO | 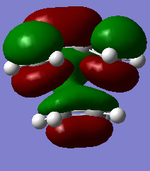
|
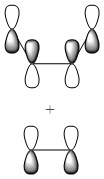
|
| HOMO | 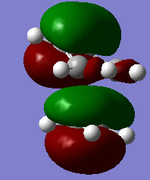
|
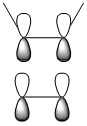
|
| HOMO-1 | 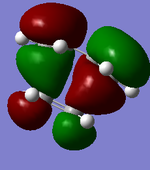
|
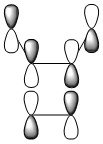
|
| HOMO-2 | 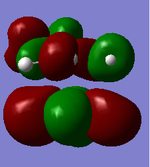
|

|
| HOMO-3 | 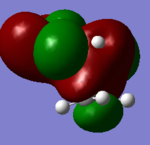
|
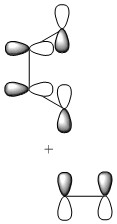
|
The transition state
File:SJ1815 DIELS-ALDER TS10.LOG
We can see that this is a transition state as it has a vibration at -948.72 cm-1 in the log file.
Two IRC calculations were run, as the first only showed progression from products to reactants, even though the graph showed entire reaction coordinates.
| IRC 1 | IRC 2 | |
|---|---|---|
| IRC graphs | 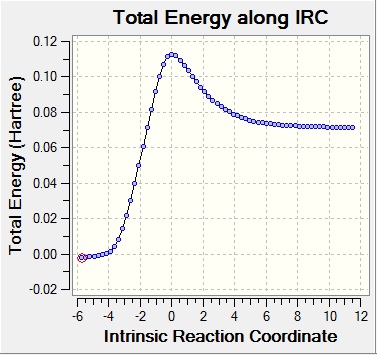
|
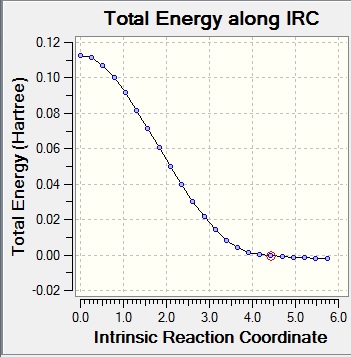
|
| IRC LOG files | File:SJ1815 DIELS-ALDER IRC.LOG | File:SJ1815 DIELS ALDERIRCFORWARDS.LOG |
| IRC animations | 
|

|
The IRC shows synchronous bond formation between cis-butadiene and ethene.
Exercise 2- Reaction of Cyclohexa-1,3-diene and 1,3-Dioxole ([4+2] cycloaddition)
Thermochemistry
| Energy | Energy difference from Reactants | |
|---|---|---|
| 1,3-dioxole | -267.068138 Hartrees/particle | X |
| Cyclohexa-1,3-diene | -233.321307 Hartrees/particle | X |
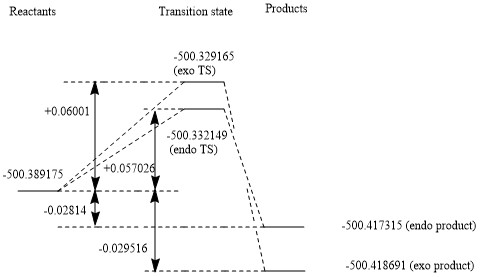
| Total Reactants | -500.389175 Hartrees/particle | X |
| Exo TS | -500.329165 Hartrees/particle | +0.06001 Hartrees/particle = +157.556255 kJ/mol (=+158 kJ/mol to 3s.f.) |
| Exo Product | -500.418691 Hartrees/particle | -0.029516 Hartree/particle = -77.494258.8973 kJ/mol (=-77.5 kJ/mol to 3s.f.) |
| Endo TS | -500.332149 Hartrees/particle | +0.057026 Hartrees/particle = +149.7218 kJ/mol (=+150 kJ/mol to 3s.f.) |
| Endo Product | -500.417315 Hartrees/particle | -0.02814 Hartrees/particle = -73.88157 kJ/mol (=-73.9 kJ/mol to 3s.f.) |
The thermodynamic product is therefore the exo product (the endo product has a higher energy due to steric clash within the molecule) while the kinetic product is the endo product, as the transition state is lower in energy, due to the fact that secondary orbital interactions are greater for the endo transition state.
MO diagrams
(Fv611 (talk) Good MO diagrams, but you didn't show the relevant HOMO and LUMO diagrams. There also isn't much of a point in showing the two diagrams for the endo and exo conformations without discussing their differences in terms of relative MO energy.)
| Endo | Exo |
|---|---|

|

|
It can't be obtained directly from these MO diagrams as to whether the reaction proceeds via normal or inverse electron demand, as all optimisations were done on different potential energy surfaces. We can, however, say it is likely to be inverse electron demand due to the oxygen atoms of 1,3-dioxole donating electron density into the dienophile C=C. This theory can be tested by running an energy calculation on the reactants and seeing whether the HOMO is of the diene or dienophile (the HOMO is the diene for normal electron demand and the dienophile for inverse electron demand).
Nf710 (talk) 08:43, 23 February 2018 (UTC) This is description is very brief, you could have tabulated the orbitals with the MOs rater than just screen shotting the numbers
Energy calculation
As we can see here, the HOMO is purely on the dienophile, so the reaction is inverse electron demand.
This is further ratified by the LUMO of the reactants, as this is purely the diene. This is as expected for an inverse electron demand Diels-Alder reaction.
The Transition State
The transition state for this reaction is depicted below, optimised to the B3LYP level.
Endo
File:SJ1815 DIOXOLE ENDOTS B3LYP.LOG
Vibration occurs at -523.01cm-1.
Exo
File:2NDPRODUCTB3LYPTS SJ1815.LOG
Vibration occurs at -528.84cm-1.
Molecular orbitals at an iso value of 0.05
Exo HOMO:
Energy: -0.19052 Hartrees/particle (=-0.191 Hartrees/particle to 3s.f.)
Exo LUMO
Energy:-0.00462 Hartrees/particle
Endo HOMO
Energy: -0.18560 Hartrees/particle (=-0.186 Hartrees/particle to 3s.f.)
Endo LUMO
Energy:-0.00699 Hartrees/particle
There is obvious, visible secondary orbital interaction between orbitals on the oxygen atoms and those on the cyclohexa-1,3-diene's cis-butadiene fragment. This lowers the endo transition state's energy.
Nf710 (talk) 08:43, 23 February 2018 (UTC) Although it is clear you have done the work the discussion in this section is extremely brief. You have come to the correct conclusions but you could have spoek in more detial bout the theory behind the thermodynamics/kenetics of the reaction. you energies are also slightly out. I think you may have miss calculated your reactant energies.
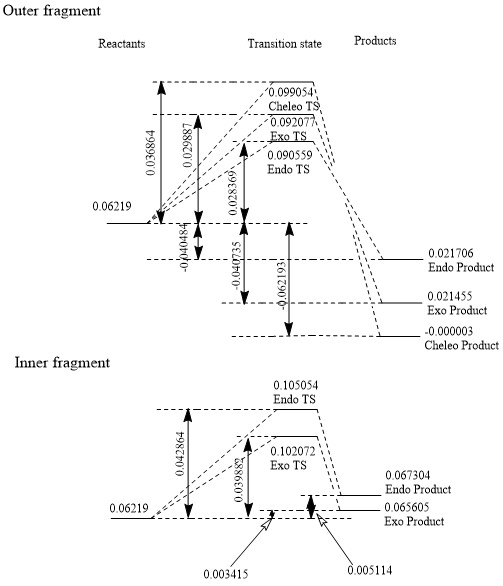
Exercise 3-Diels-Alder ([4+2]) vs Cheleotropic ([4+1])
| Cheleotropic | Outer fragment Endo | Inner fragment Endo | Outer fragment Exo | Inner fragment Exo | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Products | File:DA1STotherC=CSJ1815PRODUCT(Exo).LOG (This has, in fact, been named incorrectly and is endo, as stated in the table). |
File:SJ1815 PM6INNERC=C-C=CENDOPRODUCT.LOG(This has, in fact, been named incorrectly and is exo, as stated in the table). | |||||||||||||
| Transition states | File:SJ1815 PM6CHELEOTS3.LOG
Vibration occurs at -484.77cm-1. |
File:DA2NDTSFROMFROZENSJ1815(endo)(1stC=C).LOG
Vibration occurs at -333.62cm-1. |
File:SJ1815EXODA2NDC=C-C=CTS(3).LOG(This has, in fact, been named incorrectly and is exo, as stated in the table).
Vibration occurs at -453.52cm-1. |
File:SJ1815 SO2 DA TS PM6 2(1stC=C)(exo).LOG
Vibration occurs at -351.55cm-1. |
File:SJ1815 SO2 DA TS PM6 2(2NDC=C)(ENDO)(REALPM6).LOG(This has, in fact, been named incorrectly and is exo, as stated in the table).
Vibration occurs at -482.80cm-1. | ||||||||||
| IRC graphs | 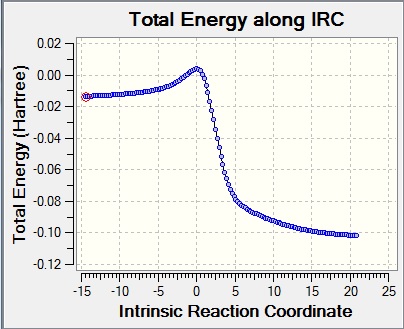
|

|

|

|

| ||||||||||
| IRC animations | 
|
|
|
|
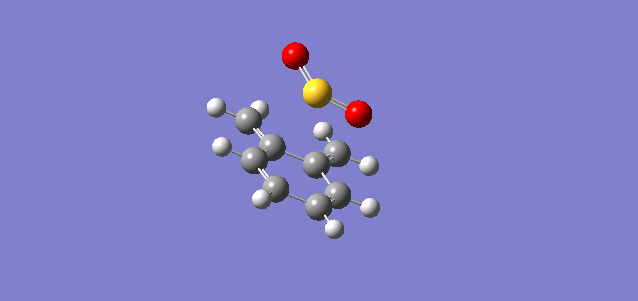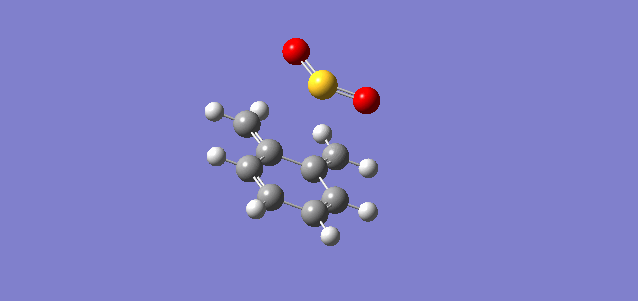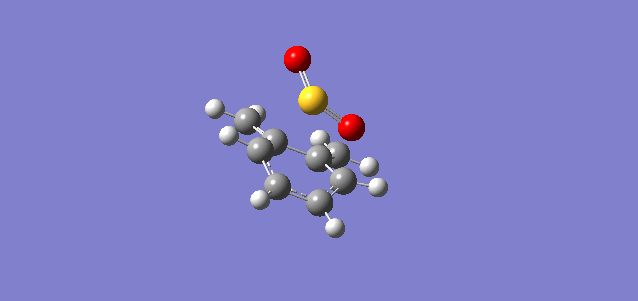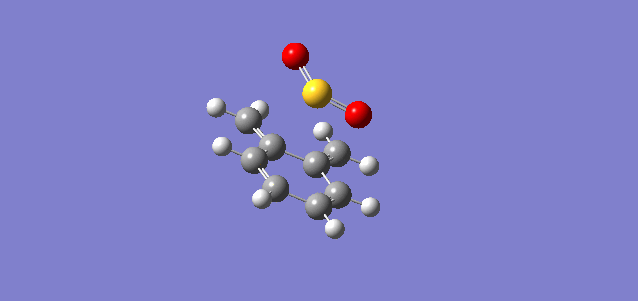
File:SJ1815INNERC=C-C=CENDOIRCPM6.LOG(This has, in fact, been named incorrectly and is exo, as stated in the table). |
(This table is so large it's actually broken the page. You should consider splitting it into multiple tables Tam10 (talk) 16:30, 19 February 2018 (UTC))
Xylylene is highly unstable as the bonding changes from 4 distinct double bonds to an aromatic ring and 2 single bonds pointing out of the ring. Due to the stability of the aromatic ring, xylylene may form a 4 membered ring to establish aromaticity or may polymerise.
Thermochemistry
(Best to convert these energies to kJ/mol before putting them in the profile Tam10 (talk) 16:30, 19 February 2018 (UTC))
Outer fragment thermochemistry
Cheleotropic
Reaction barrier= +0.036864 Hartrees/particle or +96.786432 kJ/mol (=+96.8 kJ/mol to 3s.f.)
Reaction energy= -0.062913 Hartrees/particle or -163.2877215 kJ/mol (=-163 kJ/mol to 3s.f.)
Endo Diels-Alder
Reaction barrier= +0.028369 Hartrees/particle or +74.4828095 kJ/mol (=+74.5 kJ/mol to 3s.f.)
Reaction energy= -0.040484 Hartrees/particle or -106.290742 kJ/mol (=-106 kJ/mol to 3s.f.)
Exo Diels-Alder
Reaction barrier= +0.029887 Hartrees/particle or +78.4683185 kJ/mol (=+78.5 kJ/mol to 3s.f.)
Reaction energy= -0.040735 Hartrees/particle or -106.9497425 kJ/mol (=-107 kJ/mol to 3s.f.)
The thermodynamic product is the cheleotropic product (it's lowest in energy) and the kinetic product is the endo product (the transition state is lowest in energy).
Inner fragment thermochemistry
Endo Diels-Alder
Reaction barrier= +0.042864 Hartrees/particle or +112.539432 kJ/mol (=+113 kJ/mol to 3s.f.)
Reaction energy= +0.005114 Hartrees/particle or +13.426807 kJ/mol (=+13.4 kJ/mol to 3s.f.)
Exo Diels-Alder
Reaction barrier= +0.039882 Hartrees/particle or +104.710191 kJ/mol (=+105 kJ/mol to 3s.f.)
Reaction energy= +0.003415 Hartrees/particle or +8.9660825 kJ/mol (=+8.97 kJ/mol to 3s.f.)
Attack at the inner cis-butadiene fragment is disfavoured and doesn't occur.
(Your energies are consistently shifted by ~7kJ/mol which suggests a problem with your reactants Tam10 (talk) 16:30, 19 February 2018 (UTC))
Exercise 4- the ring opening of dimethyl (1R,2S)-cyclobut-3-ene-1,2-dicarboxylate
The ring opening of a 4-membered ring is only thermally allowed if the transition state is a Möbius transition state (that is, the 2 ends of the ring are conrotatory and twist in the same sense). This is due to the Woodward-Hoffmann rules, which say a thermally allowed reaction has 4n antarafacial electrons and 4n+2 suprafacial electrons[12]. To fit this requirement, the 2 ends of the cyclobutene fragment must rotate the same way, otherwise the orbitals won't be antarafacial.
This can be seen when you look at the IRC for the reaction
| IRC | |
|---|---|
| IRC graphs | 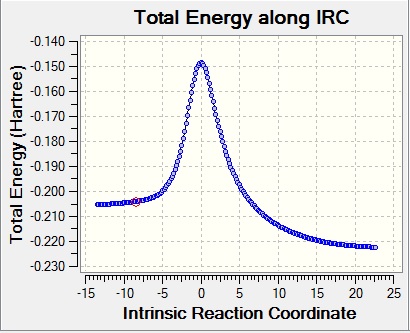
|
| IRC LOG files | File:SJ18152+2TS4IRC.LOG |
| IRC animations | 
|
The transition state
This vibration occurs at -696.41cm-1. This negative vibration confirms the fact that this is a transition state.
MO analysis
| Reactants | Products | Transition State | |
|---|---|---|---|
| HOMO | 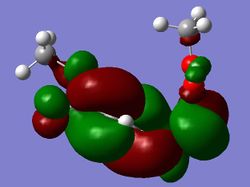
|
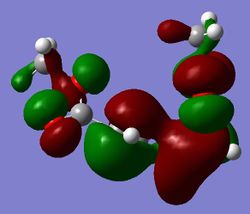
|
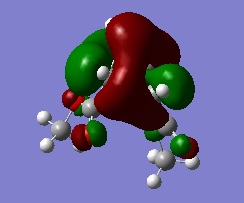
|
| LUMO | 
|
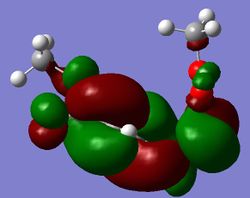
|

|
We can see from these MOs a lot of twisting in the transition state. This ratifies the Woodward-Hoffmann analysis of the reaction performed earlier.
(This is not so easy to see, especially with the opaque surfaces obscuring the atoms. Otherwise, good work Tam10 (talk) 16:30, 19 February 2018 (UTC))
Conclusions
From these reactions, we can see that endo Diels-Alder reactions are generally the kinetic product, but not the thermodynamic product, due to steric clash in the product raising the energy of the endo product. We have also seen that establishing aromaticity is a large driving force for reactions, meaning SO2 will only react in a place that establishes this aromaticity in the product. We have also seen that ring opening of 4-membered rings proceeds with conrotation, as predicted by the Woodward-Hoffmann rules and that the transition states and energies of these can be accurately calculated using Gaussian.
References
- ↑ https://chem.libretexts.org/Reference/Organic_Chemistry_Glossary/Hammond%E2%80%99s_Postulate accessed on 8/11/2017
- ↑ Michael J Bearpark, 2017, Calculating Molecular Geometries, Lecture, Quantum Mechanics 3/3rd Year Computational Chemistry Laboratory, Imperial College London, 6th November 2017
- ↑ https://www.nrl.navy.mil/mstd/branches/6390/surfaces-and-interfaces accessed on 6/2/2018
- ↑ adapted from F. Jensen in Introduction to Computational Chemistry ed. Wiley, Wiley, Indianapolis, 1st edn., 1999, ch. 5. Adaptation obtained from https://lcbc.epfl.ch/files/content/users/232236/files/lecture_2016_2.pdf accessed on 12/2/2018
- ↑ A. Szabo, N. Oatlands in Modern Quantum Chemistry ed. Dover Publications Inc., Dover Publications Inc., Mineola, 1st edn., 1996, ch. 3, pp. 156
- ↑ http://gaussian.com/semiempirical/ accessed on 8/2/2108
- ↑ http://gaussian.com/basissets/?tabid=2 accessed on 8/2/2018
- ↑ http://gaussian.com/dft/ accessed on 8/2/2018
- ↑ Stark J.G., Wallace H.G. in Chemistry Data Book ed. Hodder Education, Hodder Education, 2nd edn, 1982, ch.19, pp. 27
- ↑ http://www.science.uwaterloo.ca/~cchieh/cact/c120/bondel.html accessed on 5/2/2018
- ↑ https://physlab.lums.edu.pk/images/f/f6/Franck_ref2.pdf accessed on 11/2/2018
- ↑ J. J. Vollmer, K. L. Servis, Journal of Chemical Education, 1968, 4, 214-220