Rep:Rt1714
Introduction
Potential energy surface
A potential energy surface (PES) provides the graphical relationship between the energy of a molecule and each possible structure. [1] PES can have many directions and the most frequently used energy profile is obtained using only one coordinate. Specific points on PES can be analysed by obtaining their first and second derivatives (i.e. gradient and curvature) of energy respect to the geometric variable. Once obtained the force constant, vibrational frequency calculation can be used to confirm whether the structure is a minimum or a transition structure.
First derivative:
-F = , where F is the force pushing the nuclei to lower energy.
Second derivative:
k = , where k is the force constant.
Vibrational frequencies:
υ=, where pi = π and u =
Energy minima
In geometry optimization, the local minimum on the PES (i.e. the energy minima for the input structure) is the point where the first derivative (i.e. the gradient) is equal to zero and the second derivative (i.e. the curvature) is positive. Nothing is going to push the nuclei to go in lower energy and both the force and displacement reaches convergence. The fact that all the vibrational frequencies are positive confirms a minimum energy structure.
Transition state
Transition state is the state where the highest potential energy is achieved. Transition structure can be determined by looking for the saddle point on the potential energy surface.[2] Transition structure is the point where the gradient is equal to zero and the second derivative (i.e. the force constant) is negative. As a result, one imaginary frequency will show up.
Nf710 (talk) 13:57, 30 January 2017 (UTC) Nice use of equations! your definition of a TS is not quite right, it is a minimum in every co ordinate apart from one where it is maximum and this is the reaction co - ordinate
Exercise 1: Reaction of Butadiene with Ethylene
Frontier molecular orbital analysis:
| ETHENE | BUTADIENE | |||||
|---|---|---|---|---|---|---|
| LUMO | ||||||
| HOMO |
|
|
|
|

The MO diagram above shows that the first interaction is between the HOMO of butadiene and the LUMO of ethene and it is an asymmetric-asymmetric interaction. Similarly, the second interaction is between the HOMO of ethene and the LUMO of butadiene and it is a symmetric-symmetric interaction. These two interactions correspond to the two new sigma bonds formed in the product. The reaction is only allowed when two involved molecular orbitals have the same symmetries. Otherwise, the overall interaction will cancel out. The orbital overlap integral for a symmetric-asymmetric, a symmetric-symmetric and an asymmetric-asymmetric interaction is zero, non zero and non zero respectively.
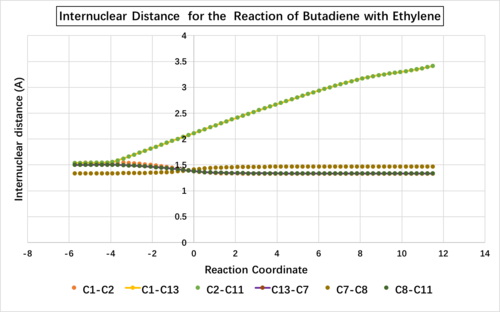
The change of internuclear distances during the reaction process:
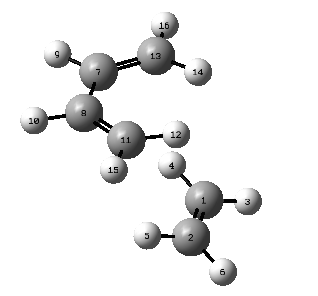
| Initial bond length | TS bond length | Final bond length | |
|---|---|---|---|
| C1-C2 | 1.327 | 1.382 | 1.541 |
| C1-C13 | 3.414 | 2.115 | 1.540 |
| C2-C11 | 3.415 | 2.115 | 1.540 |
| C13-C7 | 1.335 | 1.380 | 1.501 |
| C7-C8 | 1.468 | 1.411 | 1.338 |
| C8-C11 | 1.335 | 1.380 | 1.501 |
Along the reaction coordinate (from right to left) is the process of forming the cyclohexene from butadiene and ethylene. The point where the reaction coordinate is 0 indicates the transition structure. The C-C bond length in ethene (i.e. C1-C2) and the C-C bond length in butadiene (i.e. C13-C7, C8-C11) increase along the reaction coordinate. The three lines in the above graph almost overlap with each other as they all change from C=C double bond to C-C single bond. The C-C bond in butadeiene which changes from single bond to double bond (i.e. C7-C8) decreases its bond length. The reactants tend to approach each other along the reaction coordinate, so for C1-C13 and C2-C11, which correspond to the new forming sigma bonds, also decrease their bond lengths. The typical sp3 and sp2 C-C bond lengths are 1.54 Å and 1.34 Å while the Van der Waals radius of C atom is 1.7 Å. As shown in the table above, the partly formed C-C bonds for C2-C11 and C1-C13 have bond lengths shorter than 2 X Van der Waals radius (3.4 Å) but longer than typical sp3 C-C bond lengths as there are no initially formed C-C bonds between these two pair of atoms. The rest partly formed C-C bonds in the transition state are all between typical sp3 and sp2 C-C bond lengths.
The vibration of reaction path at the transition state:
| -948.25 cm-1 | 145.16 cm-1 | ||||
|---|---|---|---|---|---|
The vibration that corresponds to the reaction path at the transition state (-948.25 cm-1) can be described as vibrating between reactants and products. As ethene is a symmetric dienophile, each end of the double bond can act with equal probability as the electrophilic site.[3] As soon as the two reactants are at proper position, the formation of the two new sigma bonds happens very fast so we consider the formation of the two bonds is synchronous. The lowest positive frequency (145.16 cm-1) cab be described as the two reactants rotate about the reaction center in order to prevent the molecules getting to close.
Nf710 (talk) 16:17, 30 January 2017 (UTC) Good first section, very nice and consise, Your MOS diagram is really good. You could have said something about the electron demand of the reaction.
Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole
Frontier molecular orbital analysis:
| asymmetric | symmetric | symmetric | asymmetric | ||
|---|---|---|---|---|---|
| exo TS | occupied orbital | occupied orbital | unoccupied orbital | unoccupied orbital | EXO product |
 |
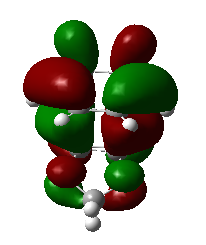 |
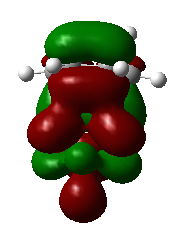 |
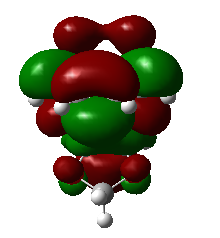 |
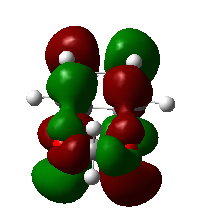 |
|
| asymmetric | symmetric | symmetric | asymmetric | ||
|---|---|---|---|---|---|
| endo TS | occupied orbital | occupied orbital | unoccupied orbital | unoccupied orbital | ENDO product |
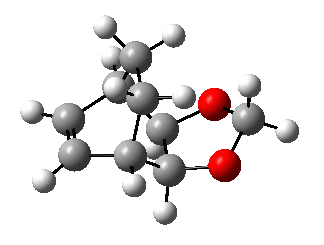
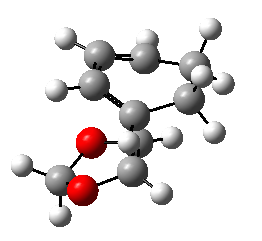 |
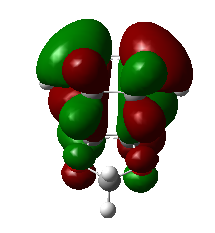 |
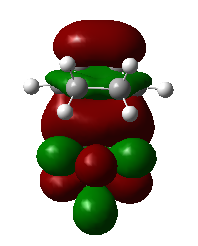 |
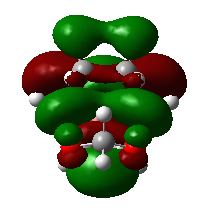 |
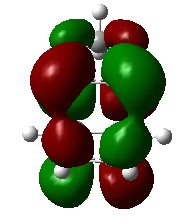 |
|
1,3-dioxole is an electron rich dienophile thus both HOMO and LUMO of dienophile will increase their energies. The difference between HOMOdienophile and LUMOdiene is closer than that between HOMOdiene and LUMOdienophile so consequently HOMOdienophile and LUMOdiene will interact much more strongly and result in an inverse demand DA reaction.
Reaction Barriers and Reaction Energies:
| Reactants (ha) | TS (ha) | Product (ha) | Reaction Energies (KJ/mol) | Reaction Barriers (KJ/mol) | |
|---|---|---|---|---|---|
| Room Temperature | -500.3816 | -500.3291 | -500.4173 | -93.73 | 137.84 |
| Reactants (ha) | TS (ha) | Product (ha) | Reaction Energies (KJ/mol) | Reaction Barriers (KJ/mol) | |
|---|---|---|---|---|---|
| Room Temperature | -500.3817 | -500.3321 | -500.4187 | -96.88 | 130.22 |
| EXO TS | ENDO TS | ||||
|---|---|---|---|---|---|
From the data shown above, one can conclude that the kinetically more favorable product is the endo-product as the reaction barrier is lower while the thermodynamically more favorable product is the exo-product as the product energy is lower. The reason why endo product is favored under kinetic control is due to the additional secondary (non-bonding) orbital interactions in the transition state. In endo-transition state, besides the bonding interaction, the blue-colored lobes on both reactants will have additional interaction and thus lower the transition state energy. In exo-TS, only primary interaction (bonding interaction) is observed.
Nf710 (talk) 16:33, 30 January 2017 (UTC) You have proved with your results that the endo is the thermo and kenetic product. This is due to the way the endo has less streic clashes. (this is because of the orientation. this is the opposite to normal). SOO had a good explaination
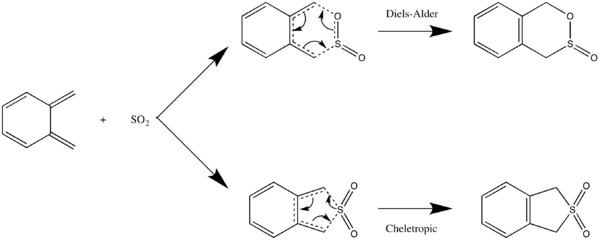
Exercise 3: Diels-Alder vs Cheletropic
TS, product and IRC calculation:
| Exo-Diel-Alder | Endo-Diel-Alder | Cheletropic reaction | |
|---|---|---|---|
| TS |  |
 |
|
| Product |  |
 |
|
| IRC |  |
 |
 |
As shown in the IRC calculation, the formation of the 2 bonds in endo- and exo-Diels-Alder reaction is asynchronous. The C-O bond formation is slightly quicker than the C-S bond formation. In cheletropic reaction, the formation of the two C-S bonds is synchronous.
Reaction Barriers and Reaction Energies:
| Reactants (ha) | TS (ha) | Product (ha) | Reaction Energies (KJ/mol) | Reaction Barriers (KJ/mol) | |
|---|---|---|---|---|---|
| Room Temperature | 0.0677 | 0.0921 | 0.0215 | -121.56 | 64.06 |
| Reactants (ha) | TS (ha) | Product (ha) | Reaction Energies (KJ/mol) | Reaction Barriers (KJ/mol) | |
|---|---|---|---|---|---|
| Room Temperature | 0.0597 | 0.0906 | 0.0217 | -99.77 | 81.13 |
| Reactants (ha) | TS (ha) | Product (ha) | Reaction Energies (KJ/mol) | Reaction Barriers (KJ/mol) | |
|---|---|---|---|---|---|
| Room Temperature | 0.0710 | 0.0991 | 0.000002 | -186.41 | 73.78 |
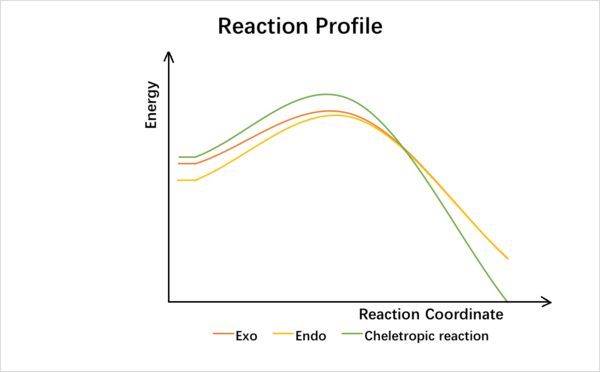
(Don't use curved lines for comparing reaction profiles. They can be very misleading - non-zero gradient at your products implies they are off the chart. Instead use dotted lines Tam10 (talk) 17:53, 27 January 2017 (UTC))
Under kinetic control, exo-product is more favorable as it has the lowest activation energy while under thermodynamic control, cheletropic product product is more favored as the product has the lowest energy.
Conclusion
Gaussian is a powerful and efficient method to carry out the molecular geometry optimizations and vibrational frequency calculations. It can locate both the energy minimum and transition structure on the potential energy surface. One shortcoming here is that it can only locate the local minimum instead of the global minimum. So during the optimization, we need to optimize from different conformers in order to get the minimum we want. Another useful calculation we used when studying the Diels-Alder reactions is the intrinsic reaction coordinate (IRC) calculation. It can provide the detailed reaction path from TS in both directions to minima and help us to understand the process more clearly. Although the Gaussian calculation is based on some quantum mechanic approximations and the results might disagree with the experimental data, Gaussian provides a useful insight of reactions pathways and molecular geometries.
References
<references> [1]
- ↑ 1.0 1.1 E.G. Lewars, The concept of the Potential Energy Surface, Computational Chemistry. DOI:10.1007/978-90-481-3862-3_2 .
- ↑ 2.0 2.1 Frank Jensen (1999), Introduction to Computational Chemistry, England: John Wiley and Sons Ltd.
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedttt