Rep:Results/Discussion Section:

The Cope Rearrangement Tutorial

Using Gaussian, we will draw an approximation of what would be the optimised structure of the 1,5-hexadiene molecule with an "anti" linkage and then with a gauche linkage. Both setch will be optimised using the HF/3-21G level of theory which usually give a good approximation of the structure with the lowest energy. Depending on the structure drawn before optimisation, we would obtain 1,5-hexadiene molecules with different anti and gauche linkage. This is due to the fact that Gaussian only founds a local minima for the drawn structure. In other words, depending on the starting molecule drawn in Gaussian and more specifically on its geometry, Ga ussian will run a calculation to find the structure with the local lowest energy. However, in order to check if our structure was close to what is expected, we checked with the litterature in Appendix 1. We obtained the following:

 anti2: https://www.ch.imperial.ac.uk/wiki/images/9/9b/Anti_opt_2.chk
 gauche3: https://www.ch.imperial.ac.uk/wiki/images/3/30/Anti_opt_1.chk

Conformer

Energy/Hartrees HF/3-21G (Experimental)

Energy/Hartrees HF/3-21G (Litterature, Script)

Point Group

Structure

Anti2

-231.69253528

-231.69260

Ci

Pentahelicene

Gauche4

-231.68961575

-231.69153

C1

Pentahelicene

The obtained conformations optimised are then compared with the ones in the appendix 1 table in order to identify the structure drawn. The previous table illustrate the comparaison between the obtained optimised structure, total energy and the litterature data. We would expect the Gauche conformation to be lower in energy than the Anti conformation optimised before since the gauche effect induces a further overall stabilisation to the molecule. This effect is mainly due to the orbital overlap which effectively makes the structure more stable in terms of thermodynamics. However, according to the computational simulation, the total energy of the optimised structure for both conformations is approximately the same. In terms of stability, they are both as stable. Nevertheless, we can still discuss why in this specific case, the gauche effect doesn't actually makes the molecule with the gauche conformation more stable than the others. The explanation could be the presence of steric clashes between the hydrogen atoms as seen on the gauche 1 conformation.

My prediction for the lowest energy conformation of 1,5-hexadiene was the anti 2 conformation. We obtained the following:

 predicted lowest energy conformation: https://www.ch.imperial.ac.uk/wiki/images/a/af/Pred_opt_2.chk

The total energy for the conformation was found to be -231.69253528 Hartrees which is effectively the lowest energy conformation for 1,5-hexadiene. According to the data on appendix 1, it was noticed that the obtained value for the optimised structure is relatively close to the litterature being -231.69254 Hartrees.

The conformation and the total energy of the optimised molecule being similar to the data given on the script, we can now proceed to a higher level of optimisation, which effectively is more accurate. We thus optimise the previous structure using the B3LYP/6-31G* level for a DFT optimisation. Comparaison between the optimised structure and obtained total energy using two different level of optimisation can be done.

 second optimisation: https://www.ch.imperial.ac.uk/wiki/images/9/9b/Anti_opt_3_f.chk

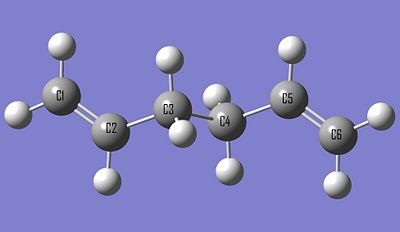
We will first look at the difference in bond angle , indeed the main modifications observed after an optimisation type process is changes in bond angles and bond length. The bond angle C4 - C5 - C6 using the basis level set is seen to be 124.81032 degrees whereas the bond angle C4 - C5 - C6 using the higher level set of optimisation giving rise to more accuracy is observed to be 125.33447 degrees. From this observation, no conclusion can be made, we therefore had to analyse the double and single bonds characteristics. For instance the C1 -C2 and C5 - C6 double bond lengths for the 3.21G method is observed to be slightly longer and therefore weaker than for the 6.31G(D) method. The small difference is due to the fact that the second method is more accurate for optimisations. Additionally, compared to the ethene double bond (1.35520 A), we notice that the double bond length of our molecule (1.31865 A) is shorter and thus stronger. Moreover, the double bond length C5 - C6 in the optimised structure 3.21G tends to have a value closer to ethene than the other. However, in general the overall geometry change between the optimised structure using these two methods is unsignificant.

The last part of this section involves the calculation of vibrational frequency for 1,5-hexadiene. No imaginary frequency has been observed which means that the actual optimised structure doesn't refer to the transition state of 1,5-hexadiene. We will now write down a list of energies under the vibrational temperatures which is found in the Thermochemistry section of the log file. The values are found to be:

the sum of electronic and zero-point energies	the sum of electronic and thermal energies	the sum of electronic and thermal enthalpies	the sum of electronic and thermal free energies
-232.830852	-232.823847	-232.822903	-232.862124

 Anti2 1,5-hexadiene molecule frequency: https://www.ch.imperial.ac.uk/wiki/images/2/26/Anti_freq_3_g.chk

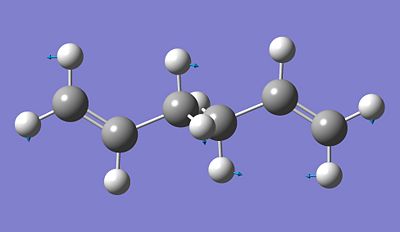
Optimizing the "Chair" and "Boat" Transition Structures

In this second part of the section we will learn how to set up a transition structure optimization by computing the force constants at the beginning of the calculation, using the redundant coordinate editor, and using QST2. Additionally, we will also visualize the reaction coordinate and run the IRC and calculate the activation energies for the Cope rearrangement via the "chair" and "boat" transition structures.

First of all, we will optimise the "chair" and "boat" transition structures for the Cope rearrangement by using two different method: Hartree Fock and the default basis set 3-21G and frozen coordinate method. Using the Hartree Fock with the default basis set 3-21G, we optimised the chair conformation and determine the vibrational frequency for its transition state after skecthing an approximation of what we think it would look like, more specifically with approximately a distance between the two allyl of 2A. We then obtained the following:

 Freq + Opt of "Chair" TS method 1: https://www.ch.imperial.ac.uk/wiki/images/9/95/Chair_conf_opt_1.chk

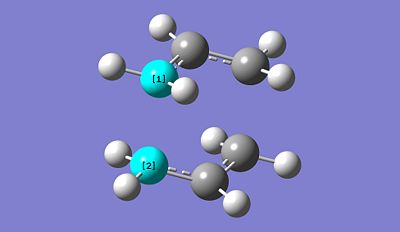
After optimisation, the distance between the two allyl fragments is found to be 2.02043A. Then using the frozen coordinate method we obtained the following:

 Freq + Opt of "Chair" TS method 2: https://www.ch.imperial.ac.uk/wiki/images/1/10/Allyl_Chair_conf_opt_freq_3.chk

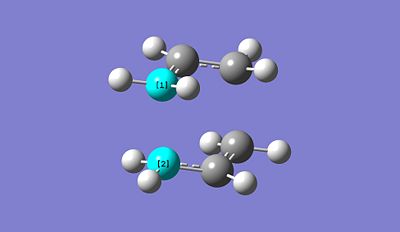
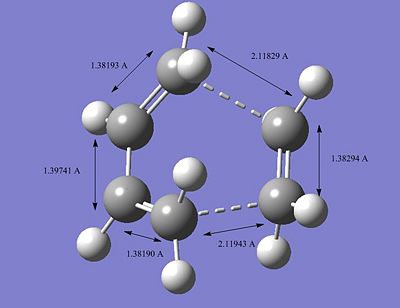
By using this second method, we notice a small distance compared to the optimised structure from the first method between the allyl fragments. The distance is found to be equal to 2.01998A. In conclusion, we can deduce that both methods allows us to optimise the TS structure with the same accuracy. The main difference between the two method is that the first one effectively runs the optimisation and calculate the vibrational frequency of the studied molecule at the same time while the second one just runs an optimisation based on the frozen coordinate defined just beforehand. It might be more reliable in some cases. One advantage of doing this, is that it may not be necessary to compute the whole Hessian once this has been done, and just differentiating along the reaction coordinate might give a good enough guess for the initial force constant matrix. This can save a considerable amount of time in cases where the force constant calculation is expensive. In terms of time, both methods are equivalent.

We will now optimise the Boat transition structure using another method being the QST2 method. In t6his method, we can actually speficy the reactants and the products in order for Gaussian to determine the transition state between them. Firstly, by trying to run an optimisation and the calculation of the vibrational frequency for its TS, we notice that the job failed. By looking at the obtained checkpoint file, we can observe that the optimised structure which failed look similar to the chair TS structure. However, the distance between the two fragments is more important than for the actual optimised chair TS structure determined previously. Indeed, the distance is observed to be equal to 3.12355A instead of 2.02043A for the previous chair TS structure.

 Boat optimised TS using QST2: https://www.ch.imperial.ac.uk/wiki/images/e/ea/QST2_1.chk

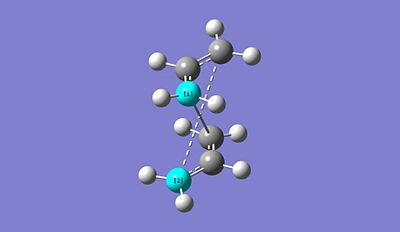
The major reason why the optimisation process failed is that by specifying which fragment is the reactant and which one is the product, we didn't actually ordered both reactant and product in a sensible way to look slightly like the predicting boat TS structure. In other word, if we can set up both reactant and product in a sensible way for the pericyclic reaction to occur, the optimisation would effectively proceed. We therefore modified the reactant and the product geometries so that their structure are closer to the boat transition state structure. We then reoptimise the structure and obtain the following:

 Boat optimised TS using QST2 after modifying the geometries: https://www.ch.imperial.ac.uk/wiki/images/1/11/QST2_2.chk

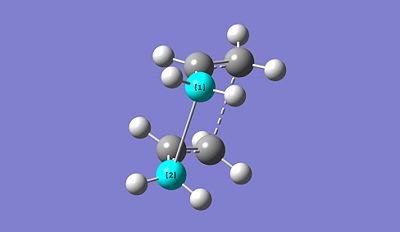
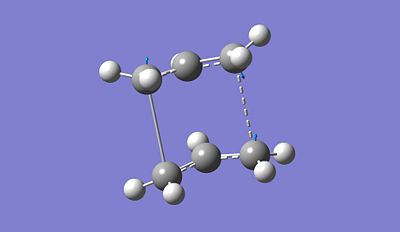
The presence of an imaginary vibrational frequency proves that the optimised structure refers to the boat TS structure. It is found to be around 840.88 cm-1. Furthermore, by looking at the vibrational frequency, we can notice that the actual vibrations induces the creation of the new bonds. It effectively confirms our theory. Additionally, in terms of bond distance, compared to the failed optimised structure, both reactant and product are much closer (2.77721A) which makes sense since the overlap between the HOMO of one fragment and the LUMO of the other induces the formation of new bonds. Since Gaussian is simply a program, to obtain the boat TS structure, we had to reorganise the reactant and product so that they are closer to the predicted final structure.

Furthermore, in order to follow the minimum energy path for a transition structure down to its local minimum on a potential energy surface, we can proceed a Intrinsic Reaction Coordinate (IRC) method. The aim of using this method is to determine the lowest energy conformation for the product. Indeed, in the graphs below, the last point refers to the total energy of the final product which should match up with the total energy of one gauche conformation after optimisation(appendix 1). After running the IRC, we found that our molecule hasn't reached a minimum geometry yet. This leaves us three options, we choose to take the last point on the IRC graph and run an optimisation. The first IRC only involved 27 points along the graph. Another IRC is run, more accurate since this time 47 points would be taken into account.

 IRC for the chair TS: https://www.ch.imperial.ac.uk/wiki/images/b/b4/Allyl_Chair_conf_IRC_1.chk
 Optimised TS after IRC: https://www.ch.imperial.ac.uk/wiki/images/4/4a/Allyl_Chair_conf_IRC_1_opt.gjf

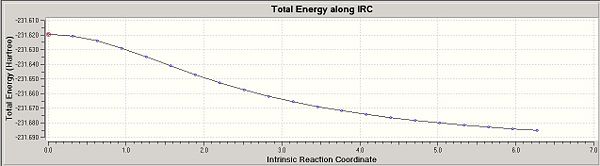
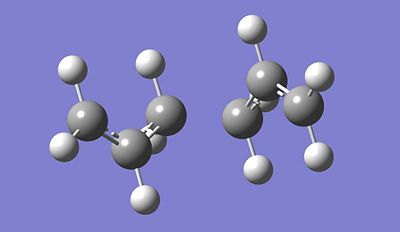
After running the IRC and optimising the Chair TS conformation, we observe that the obtained product look similar to the gauche conformation of the compound. Indeed, by looking at its total energy, we can effectively correlate it to the total energy of the gauche 4 conformation with a total energy of -231.69166701 Hartrees. From this, we can deduce that the reactant (chair conformation) goes via the transition state determined previously and tghe product formed is the Gauche 4 conformation according to the IRC and optimisation process done in this section.

Finally we calculated the activation energies for our reaction via both transition structures (chair and boat TS) by reoptimising and calculating the vibrational frequency for both structures with a more accurate method: B3LYP/6-31G* level of theory. To check if we obtained the transition state, we just checked if there was any imaginery vibrational frequency. For this second optimisation, we used the HF/3-21G optimized structures which was run previously. We obtained the following:

 Freq + Opt 2 of "Chair" TS: https://www.ch.imperial.ac.uk/wiki/images/2/23/Reopt_activation_energy_chair_conf_3.chk
 Freq + Opt 2 of "Boat" TS: https://www.ch.imperial.ac.uk/wiki/images/d/d0/REOPT_ACTIVATION_ENERGY_BOAT_CONF_4.chk

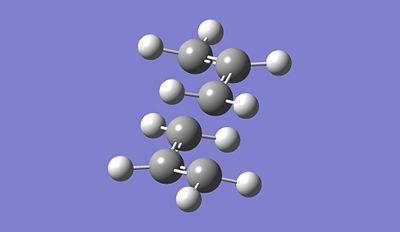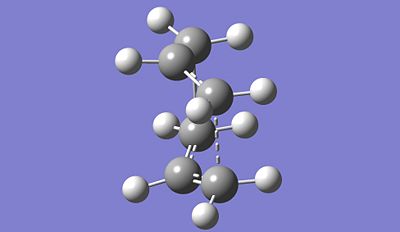	HF/3-21G	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619	-231.467	-231.461	-234.557	-234.415	-234.408
Boat TS	-231.603	-231.451	-231.445	-234.540	-234.402	-234.396
*Reactant (anti2)*	-231.692	-231.539	-231.532	-234.612	-234.469	-234.462

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.70	44.69	34.06	33.17	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	41.96	41.32	44.7 ± 2.0

After determining the total energies from the different methods and conformations, it was seen that the obtained values are similar to the data on the script exept from the difference in energy for the chaor conformation using the B3LYP/6-31G* basis set. The experimental values at 0K are relatively close to the litterature values. Additionally, from these analysis, we can effectively deduce that the anti-2 conformation goes via the transition state determined previously in order to form the gauche 4 conformation as the final product.

The Diels Alder Cycloaddition

In this section, we will characterise transition structures using the several previous methods. Addtionally, we will look at the shape of some of the molecular orbitals. The Diels Alder reaction belongs to a class of reactions known as pericyclic reactions. Indeed, the π orbitals of the dieneophile are used to form new σ bonds with the π orbitals of the diene. Whether or not the reactions occur in a concerted stereospecific fashion (allowed) or not (forbidden) depends on the number of π electrons involved. In general the HOMO/LUMO of one fragment interacts with the HOMO/LUMO of the other reactant to form two new bonding and anti-bonding MOs. The nodal properties allow one to make predictions according to the following rule:

1- If the HOMO of one reactant can interact with the LUMO of the other reactant then the reaction is allowed. 2- The HOMO-LUMO can only interact when there is a significant overlap density. If the orbitals have different symmetry properties then no overlap density is possible and the reaction is forbidden.

For all optimisation run, the AM1 semi-empirical molecular orbital method is used. Firstly, we determined the HOMO and LUMO of cis butadiene and characterise it to be either symmetric or anti symmetric with respect to the plane.

	Molecular Orbital	Symmetry		Molecular Orbital	Symmetry
HOMO		Anti-symmetric	HOMO		Symmetric
LUMO		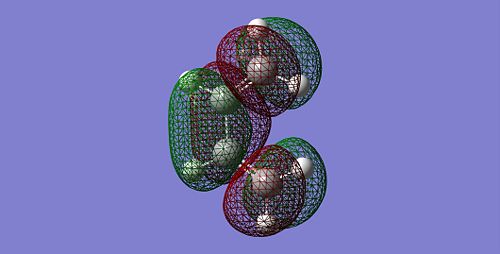Symmetric	LUMO		Anti-symmetric

We will now compute the Transition State geometry for the prototype reaction and examine the nature of the reaction path. To do so, we optimise the dienephile and the diene separatly and then paste both fragments into the same windows in Gaussian before sketching the predicted transition state. Indeed, we need to organise the geometry of both fragment so that their structure are closer to the boat transition state structure. We obtained the following:

 Optimisation of cis-butadiene: https://www.ch.imperial.ac.uk/wiki/images/b/b3/Cis_butadiene_opt_1.chk
 Optimisation of ethene: https://www.ch.imperial.ac.uk/wiki/images/3/3d/Diene_opt_1.chk

From the previous Molecular Orbitals, we effectevely notice that the HOMO of the Cis-butadiene matches up with the LUMO of the Ethylene. This overlap induces the formation of the expected new bond and allows the cycloaddition to occur. In other words, the formation of new bond in this specific case of cycloaddition occur between the HOMO of the diene and the LUMO of the dienephile. To determine the structure of the transition state associated with this cycloaddition reaction, we optimised both dienephile and diene fragment separately using the semi-empirical AM1 method to optimise the structure. Then we copy and paste both fragment into a new window and try sketching what we think would be the transition state structure. Indeed, we modified their geometries so that their structure are closer to the transition state structure, otherwise Gaussian would not be able to optimise the transition state and determine its vibrational frequency as well as its imaginery frequency. The starting geometries of both fragment should be relatively close to the TS structure. Here is our starting geometry:

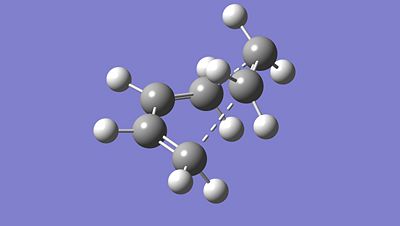
 Optimised TS: https://www.ch.ic.ac.uk/wiki/images/6/67/Cycloaddition_opt_freq_1.chk

After optiimising the TS, we compared the bond distances of the TS to the typical sp3 and sp2 C-C bondlengths. A typical sp2 C-C bondlength is approximately found to be 1.35520A and a typical sp3 1.54000A. The C=C bondlength in the dienephile (1.29343A) is much shorter than a typical sp2 C-C bondlength and thus stronger. The same observation is made for the sp2 C-C bondlength in the diene (1.33507A). On the other hand, the sp3 C-C bondlength for the forming bonds are higher (~2A). To obtain a better understanding of the difference between these values from the TS and litterature ones, we need to look at imaginery vibrational frequency. In fact, when the double bonds of both diene and dienephile vibrates in a way that makes them shorter, the sp3 C-C bondlength are effectively getting longer. Thus, the observation made previously is due to the fact that the bonds are vibrating in a way that make the bonding possible, also in terms of molecular orbitals matching (HOMO and LUMO interaction). The HOMO of the diene (butadiene) interacts with the LUMO of the dienephile (ethylene) to allow the formation of the bonds. The interaction between the HOMO and LUMO is clearly seen in the pictures above. Finally, we observe that the TS HOMO is found to be symmetric with respect to the plane going through the centre of both fragments.

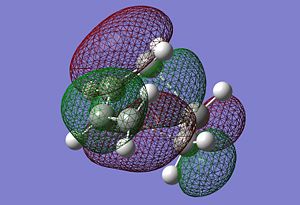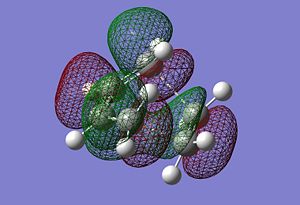Furthermore, the van der Waals radius of an atom is the radius of an imaginary hard sphere which can be used to model the atom. The actual van der Waals radius of the C atom is found to be 1.70A. In other words, if the distance of the bond formed via the transition state is less than twice the C van der Waals radius, the bonding will effectively be favorable and thus occur. The picture illustrating the TS C-C sp2 and sp3 bondlengths actually shows, firstly that the formation of the two new bonds is synchronous and finally that the bonding can occur since the bondlength of the forming bonds is much lower than twice the value of the C van der Waals radius (1.70A). We can therefore rationalise and understand why and how the formation of the two new bonds occur for this specific exemple.

The imaginery frequency for the transition state actually shows the formation of the two new bonds in terms of bonds vibrating. Indeed, we can clearly see the bonding process via a pericyclic reaction, morespecifically a cycloaddition. On the other hand, the lowest positive frequency only shows a simple vibration of some bonds. However, it doesn't explicite bonding formation or even the interaction between the two fragments reacting. The imaginery frequency is found to be - 957.75 cm-1 and the lowest positive frequencty 146.98 cm-1.

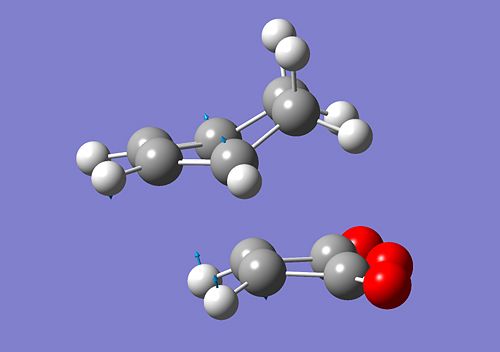
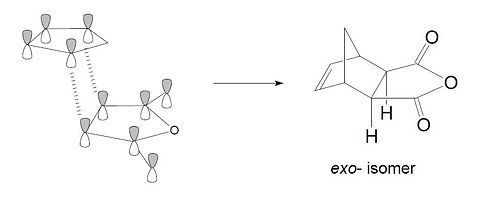
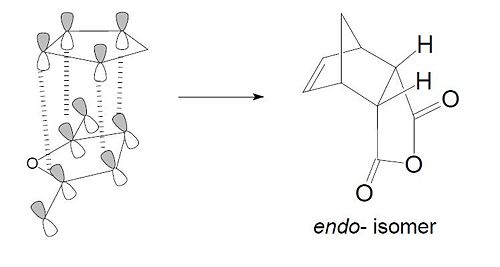
The last exemple of cycloaddition is the reaction between the cyclohexa-1,3-diene reaction and the maleic anhydride. We will follow the same procedure and use the same method as for the previous cycloaddition example. Firstly, we had to sktech the two geometry of the two fragments (diene and dienephile) and optimize it using the semi-empirical AM1 method. The two optimised fragments are shown below:

 Optimised cyclohexa-1,3-diene fragment: https://www.ch.ic.ac.uk/wiki/images/8/83/Diene_opt_1dc.chk
 Optimised maleic anhydride fragment: https://www.ch.ic.ac.uk/wiki/images/a/aa/Dienephile_opt_1.chk

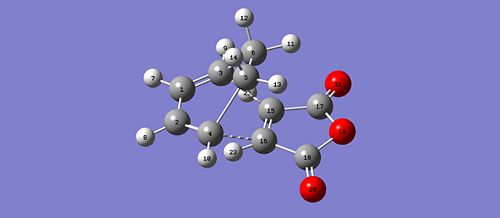
The interaction of the cyclohexa-1,3-diene HOMO with the maleic anhydride LUMO will give rise to a cycloaddition type reaction and thus the formation of new bonds. After running an optimisation and a calculation for the vibrational frequency using the same method as before, we obtain two conformers, depending on the orientation of the maleic anhydride. Additionally, as for the previous cycloaddition, for the optimisation process to proceed, we effectively need to to modify the geometries of both diene and dienephile so that they are close to the predicted TS for Gaussian to proceed. The bonds are formed between C4 - C16 and C3 - C15. The formation of these bonds can be verified by looking at the imaginery frequency obtained from the vibrational frequency calculation. We obtained the following:

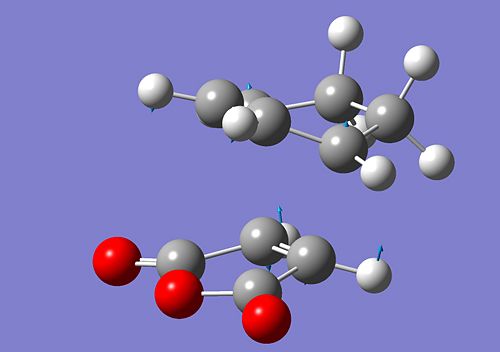The presence of imaginery frequencies in the obtained checkpoint files for both endo and exo product proves that the structures below are actual transition states. Moreover, by looking at the bondlengths we can explain why the exo form is found to be more strained than the endo conformation. The imaginery frequency is found to be -806.36 cm-1 for the endo conformer and -812.13 cm-1 for the exo conformer. As before, the lowest positive vibrational frequency isn't related to the bond forming. Indeed, it refers to a simple vibrational mode of some bonds. Additionally, we can compare the total energy for both conformer and comment on any differences.

	Endo conformer	Exo conformer
Total energy - Harthrees	-0.05150479	-0.05041984

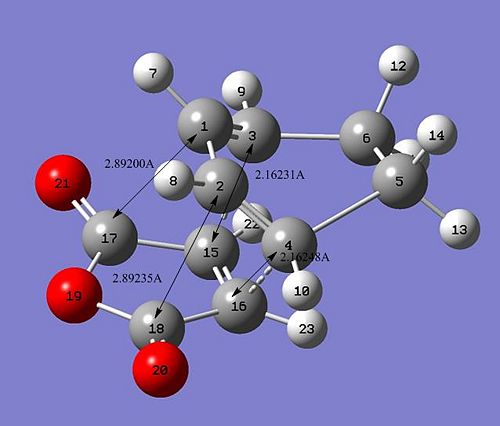Either in terms of total energy and bondlengths, there is a small difference between the endo and the exo conformers. In fact, the endo conformer is slightly lower in energy than the exo conformer. We can rationalize this observation firtly by looking at the bondlengths. In the case of the endo conformer, we notice that the diene and the dienephile are more distant. Indeed, the HOMO and LUMO of both conformers gave us a better understanding of this difference in energy, notably in terms of secondary orbital overlap (Shown below). Indeed, since there is no secondary orbital overlap for exo conformer, the total energy of the molecule would be slightly higher and thus less stable in terms of thermodynamics. The secondary orbital overlap explains why the bondlengths in the endo conformer are shorter than the exo one. Both fragments need to be as close as possible for the diene HOMO and the dienephile LUMO to interact. We can therefore conclude that the exo conformer is the more strained. Additionally, the nodal plane present on each conformer confirms the fact that their symmetry is anti-symmetric. The nodal plane is found in the C-C through space distances between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” -CH2-CH2- for the exo and the “opposite” -CH=CH- for the endo.

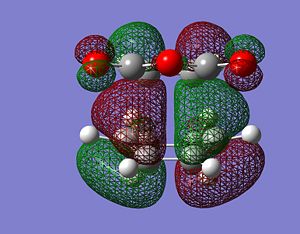Exo product, No secondary orbital overlap

	Molecular Orbital	Symmetry		Molecular Orbital	Symmetry
HOMO Endo conformer		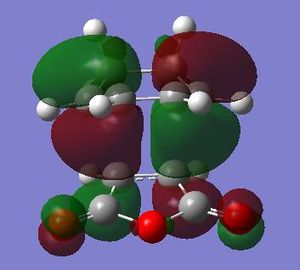Anti-symmetric	HOMO Exo conformer		Anti-symmetric
LUMO Endo conformer		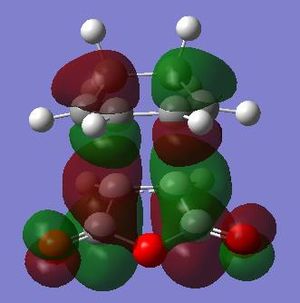Anti-symmetric	LUMO Endo conformer		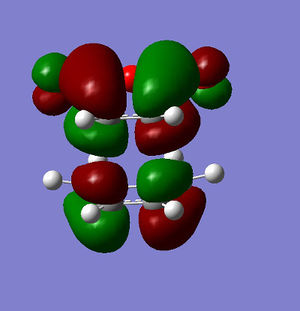Anti-symmetric

 Optimised (+freq) endo conformer: https://www.ch.ic.ac.uk/wiki/images/7/75/Opt_ex3_part3_reaction_opt_freq_endo.chk
 Optimised (+freq) exo conformer: https://www.ch.ic.ac.uk/wiki/images/3/3f/Opt_ex3_part3_reaction_opt_freq.chk

Key literature

http://www.umd.umich.edu/casl/natsci/chem/decamp/c226/Secondary%20Orbital%20Overlap.pdf
J. Org. Chem., 1987, 52 (8), pp 1469–1474 DOI: 10.1021/jo00384a016
Organic Pericyclic Reactions, Henry Rzepa, second year lecture notes