Rep:RWCOMPTSPAGE

Transition States

Introduction to Methods used

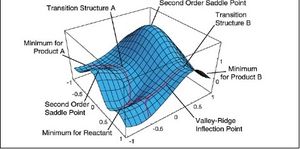
The potential energy surface for the species involved in a reaction has many local maxima and minima as well as a global maxima and minima. The minima often correspond to thermodynamically stable geometries such as the products or reactants of a chemical reaction. Conversely, the local maxima correspond to points of highest energy such as transition states of chemical reactions. They are only maxima for the minimum energy pathways. It was noted in the frequency analysis for the transition states that the vibration corresponding to a successful transition state was a negative frequency. This is because the force constant is the second derivative of the PES and this is shown in the equation below. Where δ=d

$F_{\mathrm{r}}^{{\mathrm{\text{'}}}^{\prime }}=-d{e}_{\mathrm{r}}^{\mathrm{2}}/d{e}^2$

Nf710 (talk) 21:59, 28 November 2017 (UTC) A TS is a saddle point. And you need to understand that the umber of dimensions in the PES is the same as the number of degrees of freeedom in the molevule 3N-6.

According to the quantum harmonic oscillator model, the Hamiltonian energy is equal to a term that has the square root of the force constant over the atomic mass as one of the terms. At a transition state, the slope and hence the gradient is coming from the highest point and so the gradient and double derivative will be negative so the force constant will also have to be negative. As you cannot get the square root of a negative number it means this frequency is an imaginary frequency or a complex number.

Nf710 (talk) 21:59, 28 November 2017 (UTC)It is not the energy is is the frequency

Figure 1.1: Labelled Potential Energy Surface

Some understanding of the transition state geometries is very useful in order to gauge an understanding of how to obtain energies and exact geometries for the transition states. A good description of how the reactants approach each other and their orientation is required to obtain an optimised transition structure and, therefore, a clear picture of the reaction profile. During this experiment, a variety of methods could be used for obtaining this transition structure. Method one was a guess at the transition structure and a direct optimisation of this to arrive at the saddle point. Method two involved first optimising this guess at the transition state to a local minimum with select frozen co-ordinates and a subsequent optimisation to obtain the desired structure. Method three involved first creating the product, optimising this structure, then breaking the bonds that are formed in this reaction and moving the two species apart to a different distance that is just outside the typical bond lengths of a transition state. This formed a structure resembling the transition state and from this point method two was carried out. Method three was the most indirect method by starting from the reactants or the products, but by far the most reliable as the initial guesses had to be very good in order for method one or two to lead to a successful formation of the transition state. The correct orientation of the reacting molecules in method 3 is simple to get right as the estimate was created from the product, and so a detailed knowledge of the transition state was not required. It could be argued that this method would only work reliably starting from the products if there is a late transition state for that particular reaction but no problems were encountered for method 3 in this investigation. For all the reactions except for that in exercise 1, method three proved to be the best method. This is a result of the species being more complex, and so, a direct route to the optimised transition structure became more difficult. Furthermore, in Exercise 2, the transition state, product and reactants were optimised using two different levels of optimisation, PM6 and B3LYP/6-31G(d) respectively.Intrinsic Reaction Co-ordinate (IRC) calculations were carried out to illustrate the progress of the reaction from one local minimum, through the transition state saddle point, and to another minimum.

The PM6 level of optimisation is much quicker but less accurate that that of the B3LYP/6-31G(d). The two have different reference points for the calculated energies under the heading 'Thermochemistry' and this is why it was essential that all calculations for a molecule were carried out at the same optimisation level as the values between different methods cannot be compared as the process is different for the different methods.

Nf710 (talk) 22:01, 28 November 2017 (UTC) This is correct, good understandung

Basis Sets used

The semi-empirical PM6 method has pre-set values for certain common integrals obtained from previous experiments that it knows. This reduces the number of integrals that need to be evaluated, thus, significantly reducing the time required for the program to run but decreasing the accuracy of the result as certain values are assumed to be certain values. The DFT B3LYP/6-31G(d) level of optimisation has a hamiltonian that is a function of charge density. Below is the exchange correlation part of the Hamiltonian for the B3LYP method. This is the part of the Hamiltonian that cannot be solved analytically with Density Functional Theory and so the integrals are evaluated via the Hartree-Fock method

$E_{\mathrm{x}\mathrm{c}}^{\mathrm{B}\mathrm{3}\mathrm{L}\mathrm{Y}\mathrm{P}}=E_{\mathrm{x}}^{\mathrm{L}\mathrm{D}\mathrm{A}}+a_0(E_{\mathrm{x}}^{\mathrm{H}\mathrm{F}}-E_{\mathrm{x}}^{\mathrm{L}\mathrm{D}\mathrm{A}})+a_{\mathrm{x}}(E_{\mathrm{x}}^{\mathrm{G}\mathrm{G}\mathrm{A}}-E_{\mathrm{x}}^{\mathrm{L}\mathrm{D}\mathrm{A}})+E_{\mathrm{c}}^{\mathrm{L}\mathrm{D}\mathrm{A}}+a_{\mathrm{c}}(E_{\mathrm{c}}^{\mathrm{G}\mathrm{G}\mathrm{A}}-E_{\mathrm{c}}^{\mathrm{L}\mathrm{D}\mathrm{A}})$

This method uses a hamiltonian that is a function of r(the radius of a the orbitals used. These calculations have many dimensions and more depending on the complexity of the molecule. Therefore, evaluating all of the integrals in the matrix as a function of their position is extremely time consuming and this has to be carried out for each consecutive iteration of the calculation and is the major contribution to calculations taking a long time to run as it produces a complex matrix set which can be n by n large. The B3LYP function takes the Hartree-Fock method and adds some corrections, as the Hartree-Fock method overestimates the energy as electron correlation is completely ignored and it is assumed electrons do not exchange. This leads to much longer processing times when optimising using the B3LYP method relative to the PM6 level of optimisation. For example, when optimising the transition structures in Exercise 2, using the B3LYP level of optimisation the run time was between 30 and 80 minutes whereas with the PM6 level it was four minutes to 15 minutes run time. Therefore, for the purpose of qualitative analysis, the PM6 level of optimisation alone was sufficient for the majority of this investigation and certainly as structures get very complex, the run time would not be suitable within the time-constraints of a week long lab.

22:06, 28 November 2017 (UTC) In this section you are only talking about the exchange correlation. This is a really good understanding anf you have shown B3LYP is DFT method with some extra tweaks for the exchange correlation with HF and local density approximations. Well done. you have gone into a lot of detail. Hopefully you have gained some undertsanding and want to be a theoretical chemist.

Introduction to Pericyclic Reactions

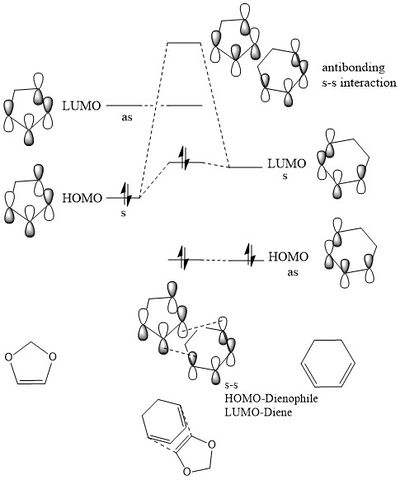
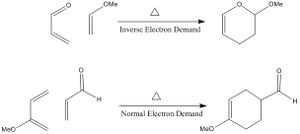
Exercises 1, 2 and 3 all involve a class of pericyclic reactions, namely [4+2] cycloadditions which would be driven by thermally allowed transition states. The Diels-Alder reactions can be classed as normal or inverse electron demand. Normal electron demand is when the strongest bonding interaction involves the combination of the diene HOMO and dienophile LUMO. This is mainly the case when the dienophile is bonded to an electron withdrawing group and the diene has an electron donating substituent. Thus, the HOMO and LUMO of the dieneophile are lowered in energy enough to have a good interaction with the HOMO and LUMO of the diene. However, if the diene is bonded to an electron-withdrawing group and the dieneophile is bonded to electron-donating groups, raising the energy of the HOMO and LUMO, inverse electron demand will be observed. This is when the strongest bonding interaction involves overlap of the HOMO of the dienophile and LUMO of the diene. Generic examples of these are illustrated below in figure 1.2 in order to illustrate this point. Leading on, there is another type of reaction investigated in this report which is the chelotropic reaction which is introduced in exercise 3 with Sulphur dioxide reacting with the Xylene molecule. The Thermodynamics of all of the cycloadditions has been compared and analysed in this report as well as being compared to this chelotropic reaction.

Figure 1.2: Examples of normal and electron demand prototypical reactions

Exercise 1

Butadiene and Ethene

The Diels-Alder reaction between Butadiene and Ethene is a (4+2) thermally allowed reaction according to the Woodward-Hoffman rules. It contains a 4πS and a 2πS component. Traditionally, this reaction probably wouldn't work due to the requirement of an electron withdrawing group on the dienophile. However, the reaction will be introduced here in order to introduce the methods used for this report. This is due to the symmetry of the system meaning no Exo or Endo specific products are formed. The reaction is shown below in figure 1.3. All of the molecules and transitions states were optimised and calculated using the PM6 method.

Figure 1.3: Reaction Scheme for Diels Alder formation of Cyclohexene

Visualizing the Real MO's

Ethene HOMO and LUMO	Butadiene HOMO and LUMO	Transition State Key Interacting Orbitals

MO Diagram

Figure 1.4: Transition State MO Diagram of Diels Alder formation of Cyclohexene

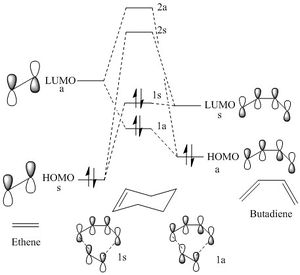
(Fv611 (talk) Good diagram, but the energy of the butadiene and ethene LUMOs should be much closer to that of the Transition State LUMO rather, as this is an intermediate case between normal and inverse electron demand. Additionally you should have labeled your TS MOs consistently between the JMol table and the diagram.)

This Frontier Molecular orbital(FMO) diagram is constructed from the HOMO and LUMO orbitals of butadiene and ethene coming together in the cyclohexene transition state. This diagram comes directly from the real MO's visualised above from the optimised transition state at the PM6 level. It is clear from the interactions present that the symmetry of the FMO's are vital to the success of an interaction. The symmetry of butadiene HOMO and the ethene LUMO are both anti-symmetric and are sufficiently close in energy in order to react. Moreover, the symmetry of the butadiene LUMO and the ethene HOMO are symmetric meaning they can react successfully as they are sufficiently close in energy.

(Fv611 (talk) The wording of the two sentences above is unclear. I know what you want to say, but it's the orbitals that are symmetric or antisymmetric, not their symmetry.)

The interaction with the symmetric orbitals appears to be stronger and lead to a larger splitting as in the MO's visualised they are the HOMO-1 and the LUMO+1. In reality, the bonding interactions would always be lower in the energy than the contributing FMO's, but due to this being a transition state MO diagram, the MO's are empirically placed at what would be the highest point in energy of the reaction. This aligns with the description of a transition state and so the bonding interactions are placed higher on the diagram than the FMO's.

The analysis that led to the placing of these MO's came from two sources. Firstly, it is known that as the conjugation of a molecule increases, the closer in energy the HOMO and LUMO orbitals. Therefore, butadiene would have a HOMO and LUMO closer in energy than the ethene. Secondly, visualising the produced MO's from the PM6 method, it was noted that the antibonding interactions for the LUMO+1 had very little character from the butadiene FMO. Moreover, the anti-bonding interaction for the LUMO had very little contribution from the HOMO FMO of the ethene and so the LUMO of the butadiene had to be closer in energy to the anti-bonding interaction.

As a result of this discussion, it must be the case that the overlap integral for a symmetric-symmetric interaction is non-zero, an asymmetric-asymmetric interaction in non-zero and a symmetric-anti-symmetric interaction is zero. As only orbital components of the same symmetry can overlap and interact and it is the symmetry necessary for a reaction to be allowed. It is this discussion that led to the Woodward-Hoffman rules that suggested for a reaction to be thermally allowed. The following equation must result in an odd number.

(4q+2)s+(4r)a = odd to be thermally allowed. This equation translates to q being equal to the number equivalent to an integer from 0 to technically infinite. In this case there is a 4πS component and a 2πS component so this value would be 1, as there is no value of q which can satisfy this value equaling 4. But there is a value of q which can satisfy the 2 π component as if q = 0 then 4(0) + 2 = 2. Therefore, as there is also no antifarcial components then this reaction is thermally allowed as this equation would equal 1, an odd number

Vibrations

In any molecule the number of vibrations can be predicted from the equation 3N-6, where N is equal to the number of bonding atoms in a non-linear molecule. In this case in the transition state, there is expected to be 42 vibrational modes as there is 16 atoms in the molecule. From analysing the first two vibrations of the optimised transition state in the formation of cyclohexene. It can be observed that the first vibration which is the imaginary vibration is clearly a vibration of the atoms taking part in the chemical reaction moving towards each other in an imaginary axis in order for the chemical reaction to take place. The symmetry of this vibration with both ends of the butadiene vibrating towards the ethene equally, suggests that the bonds in this pericyclic reaction are formed in the same step and at the same time; Which is expected in a concerted transition state. This is an example of a synchronous bond formation. It can also be observed from vibration 2 that there is no other imaginary frequencies in this optimised transition state. The vibration of the second frequency is very much in an X,Y plane and is more in line with a traditional bending mode observed in typical IR spectrums.

Bond Length Analysis

C-C Bond Type	Bond Length (Angstroms)
	Butadiene	Ethene	Transition State	1 Step before Bond formation (IRC)	Cyclohexene
C1-C2	1.33472	-	1.37977	1.49237	1.50090
C2-C3	1.46883	-	1.41111	1.34208	1.33784
C3-C4	1.33472	-	1.37977	1.49237	1.50090
C4-C5	-	-	2.11473	1.66091	1.54040
C5-C6	-	1.32725	1.38176	1.53733	1.54091
C6-C1	-	-	2.11473	1.66091	1.54040

It is clear from the table above that as the reaction proceeds, the C-C single bond present in butadiene begins to shorten to a typical C=C bond length heading towards 1.32 Angstroms as the ethene approaches the transition state and beyond geometry. Moreover, it is clear that the C=C double bonds present in butadiene and ethene begin to elongate towards the C-C single bond length similar to that of the C-C in butadiene especially at the transition state, Then onto a typical Sp3-Sp3 bond length of about 1.54 Angstroms in the final product. There is an element of symmetry present in the approach of the ethene as the bond lengths between the symmetrical bonds are the same length to 2 decimal places for all components of the reaction coordinate, and this can also be seen in the table. It is interesting to note, that the final C=C double bond distance is in-between that of ethene and butadiene. Moreover, the bond lengths predicted from the computational calculation at the PM6 level are within 10% of the literature values suggesting for a simple system the PM6 provides a good estimate of the energy over a transition state and of the reactants and final products.

Bond Length (Angstroms)
Butadiene C=C	Ethene C=C	Butadiene C-C
1.338	1.3305	1.454

Figure 1.5: Labelled Cyclohexene to illustrate the carbons the bond lengths refer to

It is also of note, that even at the transition state, all of the atoms involved in the chemical reaction are within the van der waals radii of a carbon atom. Even the carbons on the ethene with the butadiene carbons they will bond to. The Van Der Waals radius of carbon is 1.70 Å. The only time they are outside the Van Der Waals radii is before any distortion of the orbitals takes place at a distance of about <3.4 Å at the start of the IRC calculations when the the two molecules are simply approaching each other through space.

(Fv611 (talk) Again, the wording is sort of unclear. Would have been better to start the discussion from the length of the forming bonds, and relating that to the sp3 distance and the VdW radii.)

Exercise 2

Reaction Scheme

Figure 2.1: Reaction scheme for formation of Endo and Exo Products from Hexadiene and 1,3-Dioxole

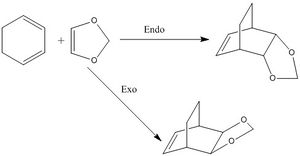
For exercise 2, the (4+2) thermal cycloaddition between Hexadiene and 1,3-Dioxole is investigated. Due to the nature of the cyclic diene, there is possibility for endo and exo products. The endo product can be identified as the dienophile approaches from below the plane of the diene and the hydrogens stick upwards in the product. Likewise, the exo product can be spotted as the dienophile approaches from above the plane of the diene and hydrogens point downwards in the final product. All MO diagrams and optimisations are presented at the B3LYP method level. Optimisations were first carried out at the PM6 level in order to get an optimised guess first and then the B3LYP method was carried out, Which shortens the length of time it takes to run the B3LYP calculations.

Molecular Orbital Interactions

Exo Transition State HOMO and LUMO	Endo Transition State HOMO and LUMO	Dienophile HOMO and LUMO	Diene HOMO and LUMO

From the B3LYP molecular orbitals it can be observed from the output that there is no interaction between the LUMO of the Oxole dienophile and HOMO of the hexadiene. This is possibly due to the fact that there is strong electron donation from the Oxole oxygens into the HOMO and LUMO FMO's which pushes them both higher in energy. This pushes the LUMO too high in energy in order to react with the HOMO of the hexadiene, so even though they are of the correct symmetry. They are not close enough in energy to interact sufficiently. Because we have in effect an electron rich dienophile, this is an inverse electron demand reaction where the strongest bonding interaction comes from the HOMO of the dienophile and the LUMO of the diene.

Nf710 (talk) 22:22, 28 November 2017 (UTC) Ho would the symetry of the orbitals tell us if it was inverse or normal electron demand

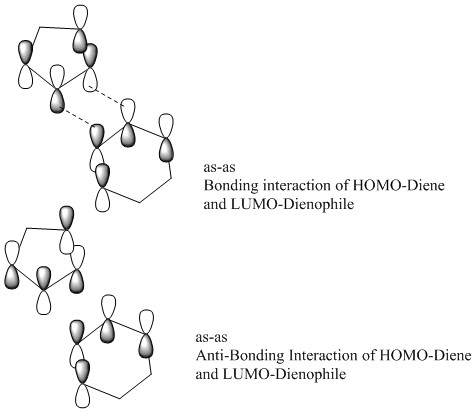
Also displayed above are the exo and endo HOMO's and LUMO's, these can be analysed to identify any potential differences in the thermochemistry of these two reactions that may explain why one is the major product. Using an MO cut off value of 0.01 and using the B3LYP orbitals. It can be observed that in the interaction of the endo transition state. There is not only primary orbital interactions between the end orbitals of the diene and dienophile. But, there is also secondary orbital interactions of the middle two orbitals of the diene with the dienophile. This extra bonding interaction may stabilise the transition state enough to lower the energy barrier. This would suggest the endo product is the kinetic product of this diels alder reaction and would be the major product. This interaction is shown above as an MO but also below in a simplified example in figure 2.2, to show how the geometry of the endo transition state facilitates this interaction. The interaction can be seen above as there is a bonding red interaction beneath the plane of the diene which is an interaction of the LUMO middle two orbitals of the hexadiene with the HOMO lone pair p orbitals on the oxygens.

Figure 2.2: Exo and Endo Products showing primary and secondary orbital interactions

From the molecular orbital interactions shown above, it is clear in the endo trajectory, that the lone pairs on the oxygen p orbitals are close enough to interact with the middle two p orbitals in the butadiene. This is a secondary orbital interaction as it does not lead to bond formation but an additional bonding interaction of same symmetry does stabilise the transition state, this interaction is displayed with the red arrows. Moreover, in the exo transition state, while the primary bonding interactions take place, the lone pairs on oxygen are now too far away to interact sufficiently to stabilise the transition state, these primary bonding interactions are shown in blue.

All of this discussion is summarised in the MO diagram below in figure 2.3 which shows the transition state energies which is why the bonding interaction is higher in energy than the contributing FMO's. It can be seen from this diagram how symmetry once again plays a part in determining the orbitals which react. However, the diagram also shows how the LUMO of the dienophile is very far away in energy to interact strongly with the HOMO of the diene even though they have the correct symmetry, an interaction does take place and this symmetry is also shown below in figure 2.4. This is an MO diagram for an exo interaction. The endo MO diagram would look very similar except the transition state bonding interaction would be slightly lower in energy in order to demonstrate how the transition state has a lower energy barrier due to the secondary bonding interactions.

(Fv611 (talk) Unfortunately you misunderstood which MOs are the HOMO and LUMO in your TS JMols, which is probably what caused your confusion in the MO diagram. You selected MOs 42 and 43 (respectively symmetric and antisymmetric, when the HOMO and LUMO are orbitals 41 and 42, which are both symmetric. You are right in that the Antisymmetric interactions do take place, between the HOMO of the diene and the dienophile LUMO, and they should have been included in your diagram. The TS LUMO definitely isn't the same as the dioxole LUMO, and you know that from the computed MOs. A comment on whether this is a normal or inverse electron demand would also have been nice.)

MO Diagram between 1,3-Dioxole and Hexadiene	Anti-Symmetric Interactions between 1,3-Dioxole and Hexadiene
Figure 2.3: MO Diagram for the transition state in the Diels-Alder reaction between 1,3-Dioxole and Hexadiene	Figure 2.4: Anti-Symmetric interactions for MO Diagram between 1,3-Dioxole and Hexadiene

Thermochemistry

Method Type	Stereoisomer Type	Activation Energy Kj Mol	Reaction Energy Kj Mol
PM6	Endo	262.90	-73.47
PM6	Exo	264.99	-73.02
B3lYP	Endo	149.70	-77.52
B3lYP	Exo	153.93	-73.92

From the thermochemistry data obtained from PM6 and B3LYP calculations. It is clear that there is a stark quantitative difference between the activation energies predicted for the Endo and Exo products. However, the qualitative interpretation is the same from both levels of calculation. The Endo product is shown to have a lower energy transition state, which would suggest that the kinetic product is formed from the Endo Transition state and we would expect the major product from this reaction to be the endo adduct. Moreover, the thermal data suggests that the Endo product is also the thermodynamic product as the resultant product is more energetically stable due to the more exothermic reaction energy. This could be caused from the secondary orbital overlap also being present in the final product and those oxygen lone pairs interacting with the carbon based orbitals may lead to a more thermodynamically stable product. It is also of note, that the difference in reaction energies between the Exo and Endo adducts is greater in the B3LYP calculation compared to the PM6 calculation. Therefore, to obtain a more quantitative description of the energy of a system, the B3LYP calculation can provide a better insight.

Nf710 (talk) This is a good section, your energies of reaction seem to be slightly too negative. However you have come to the correct conclusion and explained everything clearly. You havent shown much insight into why the endo is the kinetic product.

Exercise 3

Reaction Scheme

Figure 3.1: Reaction scheme for formation of Endo and Exo products from reaction of SO2 and Xylene

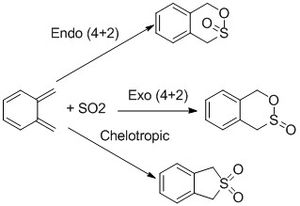
In this exercise, the (4+2) endo and exo Diels-Alder cycloadditions between sulphur dioxide and xylene are compared and contrasted with a detailed look into the thermochemistry of the system. These are both then compared to the chelotropic reaction. This produces a different product where only the sulphur is incorporated into the resulting ring and a 5-membered ring is formed. This is also a pericyclic reaction, however both new sigma bonds are formed to the same atom. These reactions are driven by the instability of xylene and the thermodynamics of this is investigated in this exercise.

Reaction Geometries

Below is attached the approaches of the SO2 at the transition state of each of the different types of the reactions as a .gif file

Reaction Type	Profile
Endo	‎‎
Exo
Chelotropic

File:PM6 SO2 OPTIMISED CHELE ABOVE TS.LOG

File:RW ENDO PM6 SO2 TS.LOG

File:RW PM6 SO2 OPTIMISED EXO TS.LOG

Thermochemistry

Reaction Type	Activation Energy kJ/mol	Reaction Energy kJ/mol
Endo	79.84	-100.96
Exo	83.824	-101.60
Chelotropic	102.16	-157.92

(You should include data for the reactants. A log file for each or their absolute energies would be useful. If you made a mistake in this table it would be hard to tell where it came from Tam10 (talk) 10:20, 24 November 2017 (UTC))

Energy Diagram for Diels-Alder and Chelotropic reactions

From the thermochemistry data presented above in a table and in an energy diagram to more clearly display the relative energies, it is clear that there is some clear differences between the energetics of Diels-Alder and chelotropic reactions. The endo product has a lower energy transition state once more, possibly due to secondary orbitals overlap. The exo is ever slightly the more thermodynamic product, possibly as there is a lesser effect from sterics but the values are very similar possibly attributed to how similar the two products are in structure. It is interesting to note that the chelotropic reaction is the most thermodynamically stable product, surprising given a smaller ring is formed, but it has a higher energy transition state and so this product would be even more of a minor product than the exo adduct. However, in equilibrating conditions and at high temperature there would be a mixture of exo and chelotropic and an investigation experimentally to determine which is the major product could lead to a useful insight.

(With such a large difference in energy between the cheletropic and both DA products, the cheletropic would probably exclusively be the thermodynamic product at high temperature Tam10 (talk) 10:20, 24 November 2017 (UTC))

Xylene Instability

Figure 3.2: Reaction scheme for formation of Endo and Exo products from reaction of SO2 and Xylene

This reaction scheme above demonstrates why xylene is so unstable. Its many reactions are driven by the fact there is an enthalpic drive to reform the aromatic benzene ring. This is a major driving force for the reactions with SO2 shown above in which the main driving force for that site being the target of pericyclic reactions is the reforming of the stable aromatic ring. There is a concerted 6-membered transition state to form the DielsAlder products and a fairly stable but higher energy transition state to form the 5-membered ring in the chelotropic product. In the IRC's for these reactions it can be observed that at the transition state there is a two 6-membered cyclic transition states forming and one highly resembles that of an aromatic system. Driving the reaction through to a thermodynamically stable product in which an aromatic ring is formed.

Second Diels Alder Site

As mentioned previously, there is a second diene site in the xylene molecule that should in theory be able to react in a Diels-Alder reaction. However, when analysing the reaction scheme as well as examining the thermochemistry data obtained for these reactions. There is very little enthalpic gain to the molecule to go through this reaction pathway as there is no aromatic ring formed as a product to the reaction and as a result a product is formed which isn't particularly thermodynamically stable.

Figure 3.3: Reaction Scheme for reaction at bad Diels-Alder Site

In the table below, it can be seen that again there is a lower energy transition state for the endo product of these Diels-Alder reactions. However, it is clear from these energies why the reactions at this site do not take place. Both of the products are in fact less thermodynamically stable than the starting reactants whereas the other site produces thermodynamically more stable products due to the re-aromatising of the benzene ring. Furthermore, the activation energies for these reactions are both higher than the normal exo and endo reactions at the other site by about 30-40 kJ/Mol so a lot more energy would have to be put into the systems to force these reactions to go. It is also interesting to note that the exo product is also not the thermodynamic product in this case as it produces a more thermodynamically unstable product than the endo reaciton.

Reaction Type	Activation Energy kJ/Mol	Reaction Energy kJ/Mol
Endo	+110.06	+14.34
Exo	+117.90	+18.77

(Well summarised Tam10 (talk) 10:20, 24 November 2017 (UTC))

File:RW PM6 B DA 2 AFTEROPT IRC.LOG

File:RW PM6 OPTIMISED B DA AFTEROPT IRC.LOG

Conclusion

In this report, various pericyclic reactions have been investigated. Most of the calculations have been completed using PM6 which while a quick and simple method. Often gave a very good indication into the energetics of a reaction system. When B3LYP was used, there was a more quantitative value obtained but the time consuming nature of these methods meant a PM6 was a very reliable and quick method to obtain good data quickly as the qualitative explanation was the same for these reactions even using the simpler calculation. Method 3 proved to be the most useful to carry out these calculations as very little information about the transition state was required in order to carry out optimisations and transition state calculations. In order to obtain better data, perhaps with more time further methods could be explored such as more complex DFT and Hartree-Fock methods.

References

<references>