Rep:Pth115TS
Introduction
Potential Energy Surface: Minima
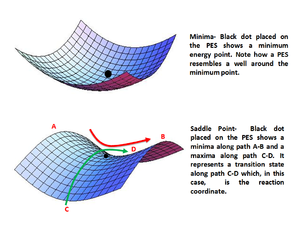
A potential energy surface (PES) is a representation of the energy of a molecule as a function of its geometrical configuration. Therefore, a molecule's potential energy is dependent on its internal coordinates[2]. A minimum on a PES (which can be local or global) corresponds to a minimum-energy geometry of a molecule and is defined as a point on the PES where the first derivative of the potential energy (V) with respect to distance (x) is equal to zero , whilst the second derivative is positive . In a chemical sense, a minimum on a PES corresponds to a stable or quasi-stable species (such as reactants, product or intermediates)[2].
The latter mathematical condition also implies that the force constant (k) has to be larger than 0 at all times since the equation holds true. As the wavenumber (v) of a bond vibration depends on the strength of the bonds , one can anticipate to obtain exclusively positive vibration frequencies for a molecule in a minimum-energy configuration.
The computational development of PESs relies fundamentally on the Born-Oppenheimer approximation, which states that due to the considerably large difference between electronic and nuclear masses, nuclei move much slower than electrons and their respective motions can be considered separately. Consequently, the overall wavefunction of a molecule may be separated into a nuclear and an electronic term.
Transition States
The transition state of a reaction is defined as the point on a PES which behaves as a saddle point. This means that that specific point behaves like a potential energy minimum in all dimensions but one, for which it behaves like a maximum[2]. Mathematically, for a system with 2 degrees of freedom (x and y), one can express these conditions as and . It is to be noted, however, that the inequalities of the second derivatives of potential energy may be switched (the former being greater than 0 whilst the latter is less than 0), depending on the nature of the saddle point.
The location of a transition state for a molecule with Gaussian can be verified by obtaining a single negative (imaginary) vibration frequency. This stems from the one negative second derivative, which corresponds to a negative force constant (as mentioned before, k is equivalent to the second derivative of the potential energy with respect to a degree of freedom).
As there are 3N-6 normal vibrational modes (and hence degrees of freedom and dimensions) for a non-linear molecule, there will be 3N-6 k values, each associated with a vibrational mode. Gaussian computes the values for k (and thus the vibration frequencies) by obtaining the eigenvalues of the Hessian matrix of 3N-6 dimensions.
Nf710 (talk) 22:08, 21 February 2018 (UTC) Good section. YOu can get all the force constants at the TS geom by diagonalising the hessian. The eigenvectors are the normal modes and the eigenvectors are the force constants. The normal modes are linear combinations of all the degrees of freedom and thats which its associated vibration looks like a bond breaking/forming.
Computations on Gaussian
Basis Sets
The computer programme Gaussian relies on the principle of the linear combination of atomic orbitals (LCAO) to estimate values for the energies for molecular orbitals (MO), using the Hamiltonian (H):. The LCAO to obtain MOs can be illustrated mathematically by the following expression: , where φi represents an atomic orbital, ci its weighting coefficient and |Ψ> the integral over an MO with which one is able to compute E with the Hamiltonian.
Nf710 (talk) 22:14, 21 February 2018 (UTC) When there is only 1 ket and not a bra-ket pair its not an integral its just a vector
PM6
PM6 optimisations utilise semi-empirical methods (which are based on the Hartree-Fock approach, amongst other approximations) to calculate the Hamiltonian. Semi-empirical approaches such as PM6 parametrise integrals based on experimental data[3]. Due to this, optimisations at PM6 are performed fairly quickly and can be used on large molecules (with complex Hamiltonian expressions), however with significant amounts of unreliability and high chances of inaccuracy.
DFT: B3LYP/6-31(d)
B3LYP calculations produce better quality and more reliable results than PM6 computations. B3LYP makes use of Density Functional Theory (DFT) to actually calculate every term of the Hamiltonian expression (apart from one term, the exchange-correlation term, for which the DFT employs the Hatree-Fock approximation). The higher precision and accuracy of the B3LYP optimisation comes at the cost of taking significantly more time to process the calculations.
Nf710 (talk) 22:16, 21 February 2018 (UTC) Really good intro! nice uses of equations to explain the basis set. You could have added some into your description of the quantum chemical meethods.
Exercise 1
(Fv611 (talk) Excellent work and thorough discussion across the whole exercise. Good job!)
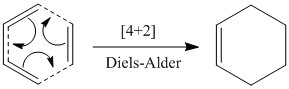
Reaction
This exercise looked at the Diels Alder reaction between 1,3-butadiene (acting as the diene) and ethene (the dienophile). The pericyclic reaction between the two molecules is a thermal [4+2] cycloaddition, indicating the number of π electrons on each of the reactants (4π e- on 1,3-butadiene and 2π e- on ethene). The reaction involves a σ-overlap between the π-orbitals of the two unsaturated compounds[4].
The ethene and 1,3-Butadiene structures were both energetically minimised at PM6 level. The minimised structures of the unsaturated compounds were subsequently used to run an optimisation of the transition state structure of the Diels-Alder reaction, again at PM6 level. An IRC of the transition state was performed at PM6, and the structure of the product of the reaction (cyclohexene) was also optimised at PM6 level.
 |
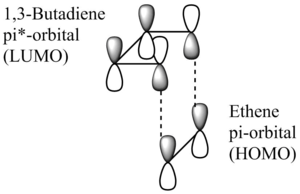 |
MO Analysis
MO Diagram

MOs: 1,3-Butadiene
| 1,3-Butadiene MOs | |||||||
|---|---|---|---|---|---|---|---|
|
|
MOs: Ethene
| Ethene MOs | |||||||
|---|---|---|---|---|---|---|---|
|
|
MOs: Transition State
| Transition State MOs | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
Discussion
The way in which the molecular orbitals of the reacting species interact is restricted, so that only orbitals of the same symmetry (antisymmetric (a) or symmetric(s)) are ab to interact with each other. When this condition is fullfilled, the reaction may be classified as 'allowed'. In the case that there are no orbitals of the same symmetry present that are able to interact with each other to lower the overall energy of the system, the reaction is 'forbidden'.
When two antisymmetric orbitals interact, the overlap integral will be non-zero. The same is true when two symmetric orbitals interact. However, should a symmetric and an antisymmetric orbital interact, the overlap integral would be equal to zero. This may be rationalised by looking at the orbital phases that overlap in each of the three scenarios. Whenever two orbitals of like symmetry overlap there is favourable constructive interference (the orbital lobes that overlap are of the same phase) leading to a non-zero overlap integral. Although, if two orbitals of opposite symmetries overlap, there would be unfavourable destructive interference (the orbitals that overlap would be of opposite phases), resulting in an overlap integral that equates to zero. The discussion about overlap integrals is summarised in the table below.
| Overlap Symmetries | Interference | Overlap Integral |
|---|---|---|
| Symmetric with Symmetric | Constructive | Non-Zero |
| Antisymmetric with Antisymmetric | Constructive | Non-Zero |
| Symmetric with Antisymmetric | Destructive | Zero |
From the MO diagram shown above, one observes that the HOMO of the 1,3-butadiene molecule and the LUMO of ethene have matching symmetries and interact to give two transition state orbitals. The same is true for the LUMO of 1,3-butadiene and the HOMO of ethene.
As expected, the formation of the transition state raises the overall energy of the system (as the electrons are now located in frontier orbitals that are higher in energy than the HOMOs of the reactants).
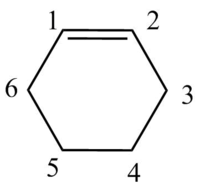
C-C Bond Lengths
Tabulated Data
| C-C Bond Lengths/Å
(Raw Information) |
C=C Bond Lengths/Å
(Raw Information) |
C-C Bond Lengths/Å
(2 decimal points) |
C=C Bond Lengths/Å
(2 decimal points) | |
|---|---|---|---|---|
| Ethene | N/A | 1.32754 | N/A | 1.33 |
| 1,3-Butadiene | 1.47077 (C2-C3) | 1.33349 (C1-C2)
1.33345 (C3-C4) |
1.47 (C2-C3) | 1.33 (C1-C2)
1.33 (C3-C4) |
| Transition State | 1.41107 (C1-C2)
2.11492 (C3-C4) 2.11452 (C5-C6) |
1.37976 (C1-C6)
1.37978 (C2-C3) 1.38176 (C4-C5) |
1.41 (C1-C2)
2.11 (C3-C4) 2.11 (C5-C6) |
1.38 (C1-C6)
1.38 (C2-C3) 1.38 (C4-C5) |
| Cyclohexene (Product) | 1.50085 (C2-C3)
1.53718 (C3-C4) 1.53458 (C4-C5) 1.53716 (C5-C6) 1.50088 (C1-C6) |
1.33697 (C1-C2) | 1.50 (C2-C3)
1.54 (C3-C4) 1.53(C4-C5) 1.54 (C5-C6) 1.50 (C1-C6) |
1.34 (C1-C2) |
 |
 |
 |
| Typical sp2 C-C Bond Length/Å | 1.34[5] |
| Typical sp3 C-C Bond Length/Å | 1.54[5] |
| C-atom Van der Waals Radius/Å | 1.7[6] |
| 2x C-atom Van der Waals Radius/Å | 3.4 |
IRC
| Animation | Graph |
|---|---|
 |
 |
Discussion
Comparing the bond lengths of the ethene molecule before the reaction and in the transition state, an extension of the C-C bond is observable. This can be accounted for by the filling of ethene's π*-orbital during the reaction, which ultimately leads to the extension and cleavage of the C-C π-bond. The hybridisation of the ethene C-atoms changes from sp2 to sp3.
As for the co-reactant, 1,3-butadiene, the collected C-C bond-length data shows a clear extension of the C1-C2 and C3-C4 bonds (originally double bonds, but single bonds after the reaction) and a contraction of the C2-C3 bond (originally a single bond, but a double bond after the reaction) as the diene reaches the transition state. This data is indicative of both C-C double bonds in 1,3-butadiene being broken during the Diels-Alder reaction, whilst a new π-bond is formed at C2-C3. Carbon atoms C1 and C4 change from sp2 to sp3 hybridisation, whereas the hybridisations of C2 and C3 remain unchanged at sp2.
In the cyclohexene product, the C-C bonds C3-C4 and C5-C6 are newly formed σ-bonds from the Diels-Alder process. In the transition state, the distances between carbon atoms C3 and C4, and C5 and C6 (2.11492 Å and 2.11452 Å respectively) are shorter than the sum two C-atom Van der Waals radii (3.4 Å). This demonstrates that there is favourable orbital overlap between the reactants that will lead to the formation of 2 new σ-bonds.
In both cases, ethene and 1,3-butadiene, the lengths of C-C double bonds that are broken at the transition state are closer in value to the bond lengths of the reactants than to the bond lengths of the products. For ethene: C-C double bond at transition state is 1.38 Å long, which is closer to 1.33 Å (reactant) than 1.53 Å (product). For 1,3-butadiene: C-C double bond at transition state is 1.38 Å long, which is closer to 1.33 Å (reactant) than 1.50 Å (product). By considering Hammond's postulate, one can deduce that we are dealing with an early transition state in this reaction (transition state resembles more the reactants than the products).
Vibrations
By inspection of the animation of the negative (and hence imaginary) bond vibration frequency at -948.86 cm-1 of the transition state, one can see that the bond formation between the diene and the dienophile is synchronous. This is as expected since the Diels-Alder reaction is concerted (i.e. all bond breaking and bond formation processes occur simultaneously).
Bond forming vibration |
Log Files
File:PTH115-CYCLOHEXENE-PM6.LOG
Exercise 2
Reaction
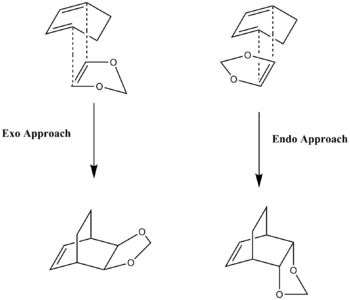
Exercise 2 investigates the Diels-Alder reaction ([4+2] cycloadition) between cyclohexadiene (diene) and 1,3-dioxole (dienophile). The reaction can take place in two ways, depending on the orientation of the reactants: exo or endo. An MO analysis, as well as a thermodynamic examination of the two different reaction pathways, was performed.
The Gaussian calculations were carried out by firstly optimising each of the reactants to a minimum, toPM6 and subsequently to B3LYP/6-31(d) level. Secondly, the reactants were placed in the exo or endo approach (with appropriate bonds frozen) and a PM6, followed by a B3LYP/6-31(d), minimum optimisation was performed. Thirdly, transition state calculations of the output from the last optimisation (with now unfrozen bonds) were done, as before first to PM6 then to B3LYP/6-31(d) level. Lastly, the output of the transition state optimisations was used to perform IRC calculations (one for exo and one for endo).
MO Analysis
MO Diagram
(Fv611 (talk) Very nice MO diagrams, could have expanded a bit more on the differences between the endo and exo conformations in terms of the relative energies of the TS MOs.)
| Endo Diels-Alder
MO Diagram |
Exo Diels-Alder
MO Diagram |
|---|---|
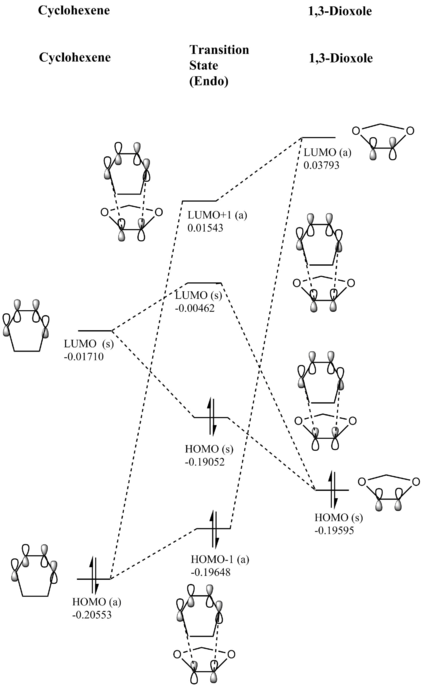 |
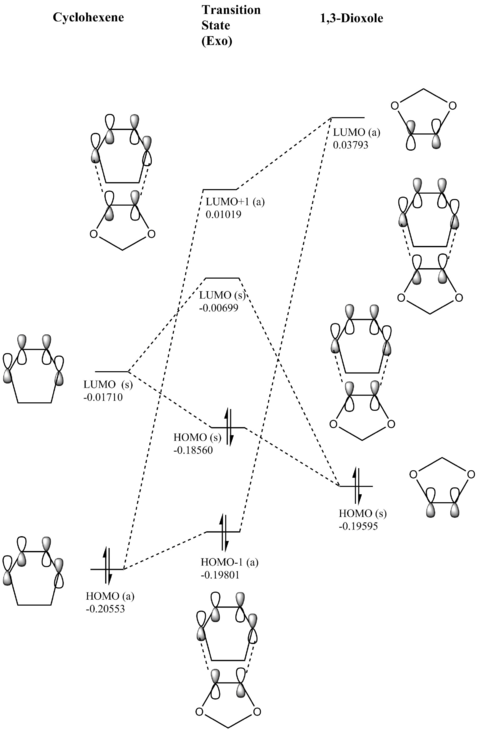 |
MOs: Exo Diels-Alder Transition State
| Exo
Transition State MOs |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
MOs: Endo Diels-Alder Transition State
| Endo
Transition State MOs |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
Electron Demand
In a normal scenario for a Diels-Alder reaction, the diene is electron-rich, whilst the dienophile is usually electron-poor. Hence, in the case of normal electron demand, the HOMO of the diene will be lower in energy than the LUMO of the dienophile (these are orbitals that interact with each other). For a Diels-Alder cycloaddition with inverse electron demand (where the diene is less electron-rich/more electron-poor and/or the dienophile is more electron-rich/less electron-poor), the HOMO is located on the dienophile and the LUMO on the diene[7].
By doing an energy calculation on both of the reactants and looking at the energies of the molecular orbitals, one sees that the LUMO is on cyclohexadiene and that the HOMO is on the 1,3-dioxole. This signifies that the Diels-Alder reaction between those two compounds takes place under inverse electron demand. A chemical reasoning for this may be that the two O-atoms attached to the double bond in 1,3-dioxole make the dienophile more electron-rich through lone-pair electron donation into the π-bond, raising the dienophile's molecular orbital energies above those of the diene.
Nf710 (talk) 22:19, 21 February 2018 (UTC) Nice discussion. However the conclusion is not that clear. it would have been clearer if you had plotted all the FMOs and then you can see them relative to each otber. But i understand what you mean.
| Dienophile HOMO | DIene LUMO | ||||||
|---|---|---|---|---|---|---|---|
|
|
Thermochemistry
Tabulated Data
| Reaction Barrier/Hartrees | Reaction Barrier/kJmol-1 | Reaction Energy/Hartrees | Reaction Energy/kJmol-1 | |
|---|---|---|---|---|
| Exo | 0.063853 | 167.65 | -0.024304 | -63.81 |
| Endo | 0.060868 | 159.81 | -0.025677 | -67.41 |
Conversion between units: 1 Hartree = 2625.5 kJmol-1
Reaction Profile
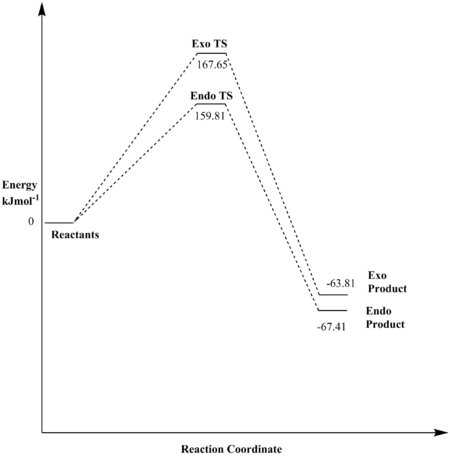
Discussion
The data shown above indicates that the endo pathway requires less energy to reach the transition state (lower reaction barrier), whilst also forming the energetically favoured product (lower reaction energy). This means that the endo reaction forms the kinetic as well as the thermodynamic product. The lower reaction barrier of the endo pathway stems from the favourable secondary orbital interactions between the lone pair on the O-atom of the 1,3-dioxole and the π-orbitals on the cyclohexadiene, leading to an overall stabilisation of the transition state. The exo transition state has no possibility to form such stabilising interactions since the 1,3-dioxole O-atoms are too far away from the diene π-system. That the endo pathway is thermodynamically more favourable may be attributed to the fact that the product formed in that reaction suffers less steric strain, as the cyclohexadiene ring and the 1,3-dioxole ring are on opposite faces. This is not the case for the exo-product, where one finds significant streic clash, thus raising the energy of the molecule.
Log Files
Note: Exo and Endo are swapped in the files below (i.e.: the .LOG file labelled PTH115-EXO-TS-B3LYP contains the endo transition state, not the exo).
File:PTH115-CYCLOHEXADIENE-B3LYP.LOG
File:PTH115-EX2-EXO-TS-B3LYP.LOG
File:PTH115-EX2-ENDO-TS-B3LYP.LOG
File:PTH115-EX2-EXO-PROD-B3LYP.LOG
File:PTH115-EX2-ENDO-PROD-B3LYP.LOG
Nf710 (talk) 22:22, 21 February 2018 (UTC) Good section. Your energies are correct and you have come to the correct conclusion. You haven't shown explicitly the secondary orbital overlap however and your discussion was quite brief. Well done on the intro.
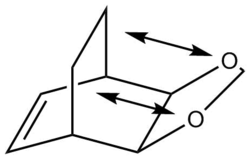
Exercise 3
Reaction
For Exercise 3, the pericyclic reactions between o-xylylene (diene) and SO2 (dienophile) are analysed. O-xylylene has two cis-butadiene sites for cycloadditions to take place (as shown in the image below): site A and site B. At site A, the reaction can take three different pathways: exo, endo or cheletropic. On the other hand at site B, only the exo and endo reactions with SO2 are examined.
All calculations and optimisations for this exercise where carried out at PM6 level.
| Reactions: Cis-Butadiene Site B | Reactions: Cis-ButadieneSite A | |
|---|---|---|
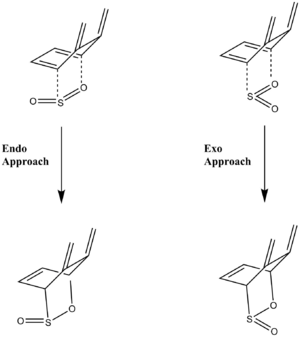 |
 |
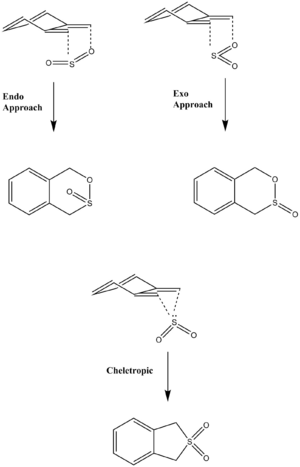 |
IRC Calculations
Reaction at Cis-Butadiene Site A
Exo:
| Animation | Graph |
|---|---|
 |
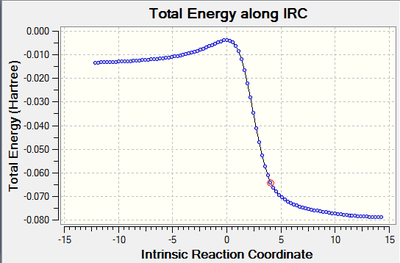 |
Endo:
| Animation | Graph |
|---|---|
 |
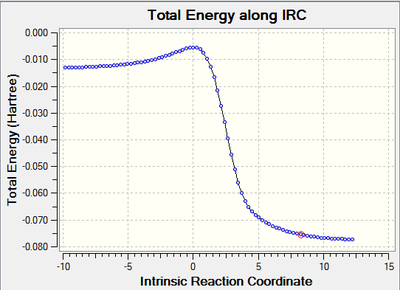 |
Cheletropic:
| Animation | Graph |
|---|---|
 |
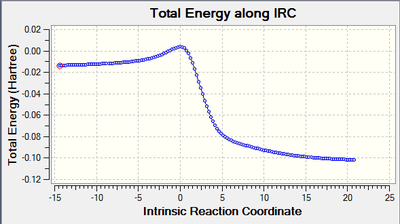 |
Reaction at Cis-Butadiene Site B
| Exo | Endo |
|---|---|
 |
 |
Thermochemistry
Reaction at Cis-Butadiene Site A
| Reaction Barrier/Hartrees | Reaction Barrier/kJmol-1 | Reaction Energy/Hartrees | Reaction Energy/kJmol-1 | |
|---|---|---|---|---|
| Endo | 0.031708 | 83.25 | -0.03715 | -97.54 |
| Exo | 0.033220 | 87.22 | -0.03740 | -98.18 |
| Cheletropic | 0.040211 | 105.57 | -0.05885 | -154.52 |
Conversion between units: 1 Hartree = 2625.5 kJmol-1
Reaction at Cis-Butadiene Site B
| Reaction Barrier/Hartrees | Reaction Barrier/kJmol-1 | Reaction Energy/Hartrees | Reaction Energy/kJmol-1 | |
|---|---|---|---|---|
| Endo | 0.043219 | 172.26 | 0.006759 | 17.75 |
| Exo | 0.046205 | 176.71 | 0.008454 | 22.20 |
Conversion between units: 1 Hartree = 2625.5 kJmol-1
Reaction Profiles
| Reaction Profile (Site A) | Reaction Profile (Site B) |
|---|---|
 |
 |
(Your endo product is a bit too high in energy Tam10 (talk) 16:46, 23 February 2018 (UTC))
Discussion
From the thermochemical data and the reaction profile of the reactions at cis-butadiene site A of o-xylylene, one can see that the cheletropic pathway has the (by far) highest kinetic barrier, but nonetheless forms the thermodynamically most favoured product. The thermodynamic stability of the product of the cheletropic reaction may be explained by the fact that the strong S=O bonds (522 kJmol-1)[8] are not being broken, which is not the case for the exo or endo reactions where one such bond is cleaved.
Further, when comparing the exo and endo pathways of the reactions at site A, it is evident that the exo reaction gives the thermodynamically (slightly) more favoured product, whilst the endo reaction has a lower kinetic barrier and thus leads to the kinetic product. The reason for this is similar to what was discussed in the Thermochemistry section of Exercise 2: secondary orbital interactions stabilise the endo path transition state.
As for the reactions at cis-butadiene site B: The endo pathway results in the formation of the kinetically as well as the thermodynamically more favoured hypothetical product. However, it is worth taking note of the considerably high reaction barriers and the endothermic nature of the exo and endo processes at site B, indicating that these reactions are very unlikely to occur in reality.
Log Files
File:PTH115-CHLERO-PROD-PM6.LOG
File:PTH115-CHLERO-IRC-PM6.LOG
File:PTH115-EX3-EXO-TS-PM6.LOG
File:PTH115-EX3-EXO-IRC-PM6.LOG
File:PTH115-EX3-EXO-PROD-PM6.LOG
File:PTH115-EX3-ENDO-IRC-PM6.LOG
File:PTH115-EX3-ENDO-TS-PM6.LOG
File:PTH115-EX3-EXO-PROD-PM6.LOG
File:PTH115-EX3-ALT-EXO-PROD-PM6.LOG
File:PTH115-EX3-ALT-EXO-TS-PM6.zip
File:PTH115-EX3-ALT-EXO-PROD-PM6.LOG
File:PTH115-EX3-ALT-EXO-IRC-PM6.LOG
File:PTH115-EX3-ALT-ENDO-PROD-PM6.LOG
File:PTH115-EX3-ALT-ENDO-TS-PM6.LOG
File:PTH115-EX3-ALT-ENDO-IRC-PM6.LOG
Further Work
Reaction
The extension dealt with the thermal 4π electrocylic reaction that forms an equilibrium between the cyclobutene and the 1,3-butadiene form. Due to ring strain, the equilibrium lies strongly to the side of the 1,3-butadiene form, so for this exercise, only the forward reaction (the ring opening of the cyclobutene form) is considered.
All optimisations were carried out at PM6 level.
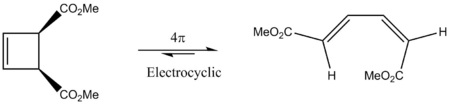
MO Analysis
MOs: Cyclobutene Ring Form
|
|
MOs: Transition State
|
|
IRC Calculations
| Animation | Graph |
|---|---|
 |
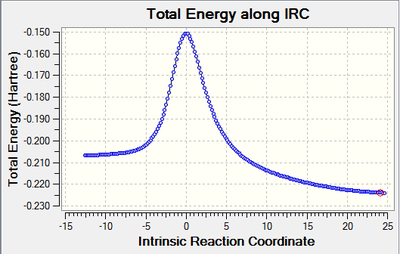 |
Analysis
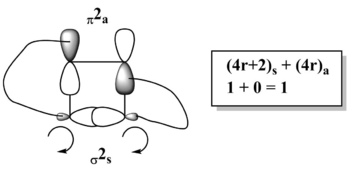
In the Woodward-Hoffmann analysis of pericyclic reactions, one makes use of the equation [9] where the (4q + 2)s term corresponds to the number of suprafacial bond formations with 4q+2 electrons, whilst (4r)a is equal to the number of antrafacial bond formations with 4r electrons, where q and r are positive integers. If the number obtained from the Woodward-Hoffmann the equation is odd, the reaction is thermally disallowed, whilst if the result is even the electrocyclic reaction is thermally allowed.
It is also known that any thermal electrocylcic reaction that involves (4n)π electrons will proceed conrotationary (meaning that the groups rotate in the same direction)[10]. Since the electrocyclic ring-opening dealt with here involves 4π electrons, it is anticipated that it proceeds in a conrotationary manner.
From the graphical Woodward-Hoffmann analysis illustrated in the image to the right (showing the HOMO of the cyclobutene ring form), one can see that the π-bond breaks in an antrafacial manner, whilst the σ-bond cleaves suprafacially. By taking into account the number of electrons in each of the processes (2 in both cases) and applying the Woodward-Hoffman equation (yielding 1, an odd number), one arrives at the conclusion that the electrocyclic ring-opening process (that produces the 1,3-butadiene form) is thermally allowed.
Moreover, by examining the lines on the analysis diagram to the right, one recognises that for the new π-bonds to form (and the shown σ-bond to break), each of the σ-bond sp3 orbitals has to rotate by 90o clockwise, explaining the origin of the conrotatory nature of the reaction.
(A lot of weird stuff happens while the groups are rotating. The mobius aromatic TS involves the rotations of pi and sigma orbitals and you don't really get what you've shown in the diagram. But a good attempt! Tam10 (talk) 16:49, 23 February 2018 (UTC))
Log Files
File:PTH115-EXTENSION-PROD.LOG
File:PTH115-EXTENSION-REACTANT1.LOG
Conclusion
The PM6 level computational investigation of the Diels-Alder reaction between ethene and 1,3-butadiene enabled us to obtain data about the energies of the reactant, transition state and product molecular orbitals. With this data, a molecular orbital diagram was constructed, with the aid of which one came to the conclusion, that only when reactant orbitals of the same symmetry can interact is a reaction considered to be allowed. Further, the bond lengths of the reacting species and the transition state were analysed to observe how and why specific bonds lengths change in the course of the cycloaddition reaction. By carrying out an IRC calculation, it was possible to determine that the bond formation process in the reaction occurs synchronously.
Exercise 2 dealt with the two different ways (exo or endo fashion) 1,3-dioxole and cyclohexadiene can undergo a [4+2] cycloaddition. B3LYP/6-31(d) optimisations on Gaussian enabled the collection of data for the molecular orbitals energies of the reacting species, the two kinds of transition states (exo and endo) and of the products formed through each reaction pathway. From this information, one was able to build molecular orbital diagrams as well as determine that the reaction proceeds through inverse electron demand. Additionally, thermodynamic data was obtained for the reaction, from which one could tell that the endo-pathway leads to the formation of the kinetic, as well as the thermodynamic product. This is attributed to secondary orbital interactions lowering the endo-reaction reaction barrier, and to less steric clash present in the endo-product.
In the next exercise, the pericyclic reactions between o-xylylene and SO2 were analysed. Both cis-butadiene reaction sites of o-xylylene were taken into consideration. By performing B3LYP/6-31(d) calculations and thus getting hold of thermodynamic data about the different reaction ways, one established that at for the reactions at o-xylylene site A, the endo product (again, due to secondary orbital interactions) is kinetically favoured, whereas the cheletropic product (due to the conservation of strong S=O bonds) dominates under thermodynamic conditions. As for site B on o-xylylene: the formation of the endo-product is preferred under both, kinetic and thermodynamic conditions.
Finally, in the form of an extension, the 4π electrcyclic ring-opening reaction of a cyclobutadiene derivative was examined. Through PM6 optimisations and an IRC computation, and a consequent Woodward-Hoffmann analysis, one could explain the conrotatory nature of the process.
Overall, the use of the Gaussian software gave us the opportunity to study a variety of aspects and the feasibility of certain pericyclic reactions. The rich amount of data obtained through the computations allowed for the in depth discussion of the mechanistic procedures of the investigated reactions.
References
- ↑ https://en.wikipedia.org/wiki/Energy_profile_(chemistry)#/media/File:Minima_and_Saddle_Point.png
- ↑ 2.0 2.1 2.2 http://vergil.chemistry.gatech.edu/courses/chem6485/pdf/pes-lecture.pdf
- ↑ http://people.chem.ucsb.edu/kahn/kalju/chem226/public/semiemp_intro.html
- ↑ http://www.ch.ic.ac.uk/motm/porphyrins/introDA.html
- ↑ 5.0 5.1 http://hydra.vcp.monash.edu.au/modules/mod2/bondlen.html
- ↑ http://periodictable.com/Elements/006/data.html
- ↑ http://www.organic-chemistry.org/namedreactions/diels-alder-reaction.shtm
- ↑ http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html
- ↑ http://www.chemtube3d.com/DAWoodward-Hoffman.html
- ↑ https://www.princeton.edu/chemistry/macmillan/group-meetings/RRK-orbital.pdf
