Rep:Physsg
Module 3: The Transistion State
Objectives
In module 1 relative energies of conformers were investigated. In this module we can move on to investigate how reactions take place i.e. bonds forming and bonds breaking. This can be done, using molecular orbital methods, numerically solving the Schrodinger equation to find transistion structures on the local shape of a potential energy surface . For this module 3 different reactions will be investigated; the Cope Rearrangement of 1,5-hexadiene and the Diels-Alder Cycloadditions of cis-butadiene with ethylene and Cyclohexa-1,3-diene with with maleic anhydride.
The Cope Rearrangement Tutorial
In the following exercise computational methods will be used in order to investigate the [3,3]-sigmatropic shift rearrangement 1,5-hexadiene.
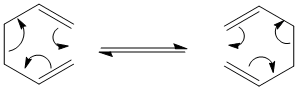
Optimisation of Reactants and Produtcs
1,5-hexadiene can exist in either an anti or gauche conformation. The optimised structures of the reactants and products need to be determined before any further investigation into the transition state structures. Therefore the anti and gauche conformers were visualised and optimised using GaussView 5.0 and their relative energies recorded.
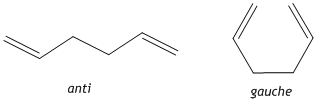
ANTI anti optimisation File Name anti1_5_hexadiene_optimisation File Type .chk Calculation Type FOPT Calculation Method RHF Basis Set 3-21G Charge 0 Spin Singlet Total Energy -231.69253528 a.u. RMS Gradient Norm 0.00001891 a.u. Imaginary Freq Dipole Moment 0.0000 Debye Point Group
Symmetrize? Point Group = Ci
Energy given in table -231.69254, in agreement with my energy Total Energy -231.69253528
GAUCHE
HF/3-21G
File Name gauche1_5hexadiene_optimisation File Type .chk Calculation Type FOPT Calculation Method RHF Basis Set 3-21G Charge 0 Spin Singlet Total Energy -231.69266118 a.u. RMS Gradient Norm 0.00001742 a.u. Imaginary Freq Dipole Moment 0.3404 Debye Point Group
Symmetrized.. Point Group = C1
Run anti2 again with B3LYP/6-31G*
anti2 high level optimisation File Name anti1_5_hexadiene_optimisation_highlevel File Type .chk Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-31G(D) Charge 0 Spin Singlet Total Energy -234.61171027 a.u. RMS Gradient Norm 0.00000985 a.u. Imaginary Freq Dipole Moment 0.0000 Debye Point Group
 |
 |
Torsion Angles (high level) C 1,2,3,4 118.54991 C 2,3,4,5 180.0 C 3,4,5,6 118.54991
Torsion Angles (low level) C 1,2,3,4 114.66878 C 2,3,4,5 180.0 C 3,4,5,6 114.66878
Vibrational analysis of anti2
B3LYP/6-31G*
Modes all positive and real
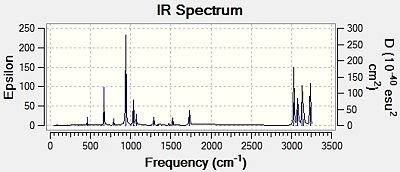
Sum of electronic and zero-point Energies= -234.469203 Sum of electronic and thermal Energies= -234.461856 Sum of electronic and thermal Enthalpies= -234.460912 Sum of electronic and thermal Free Energies= -234.500777
Freq analysis ran at lower basis set for activation energies [later].
Sum of electronic and zero-point Energies= -231.539539 Sum of electronic and thermal Energies= -231.532565 Sum of electronic and thermal Enthalpies= -231.531621 Sum of electronic and thermal Free Energies= -231.570916
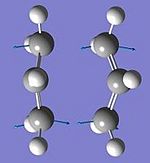
Optimising the Chair and Boat Transistion Structures
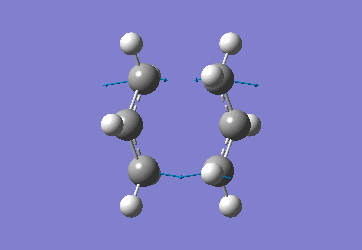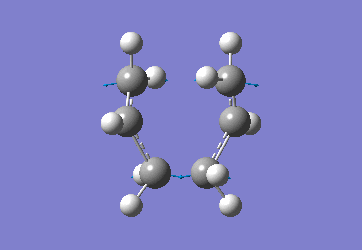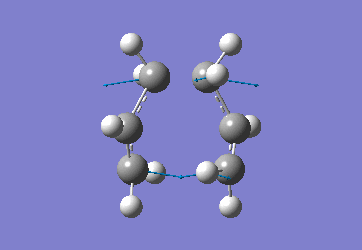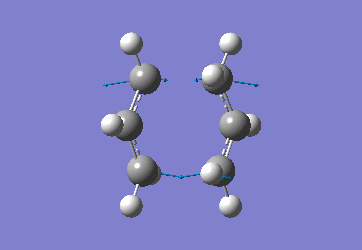
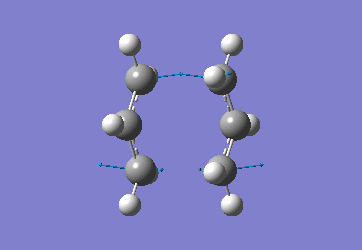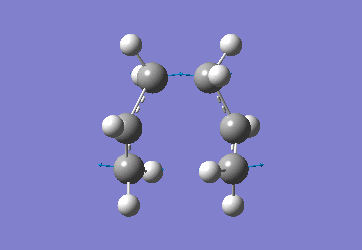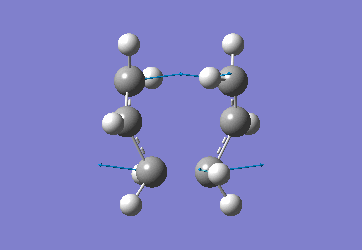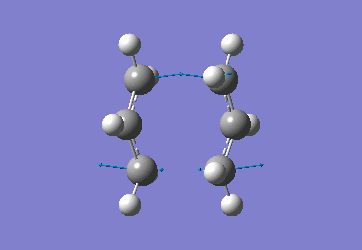
Chair Optimised to a TS (Berny)
C-C [terminal] = 2.02055 Imaginary vibration at 817.9cm-1 Optimised using frozen method
 |
 |
Boat
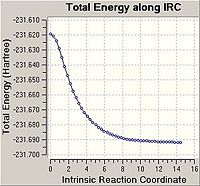 |
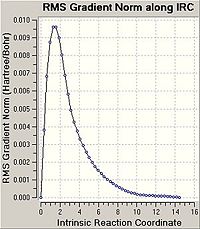 |
The Diels-Alder Cycloaddition
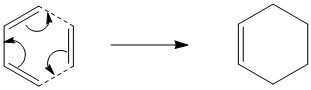
Optimisation and Analysis of cis-butadiene and ethylene
cis butadiene opt File Name cis-butadiene-opt File Type .chk Calculation Type FOPT Calculation Method RPDDG Basis Set ZDO Charge 0 Spin Singlet Total Energy 0.04616719 a.u. RMS Gradient Norm 0.00013689 a.u. Imaginary Freq Dipole Moment 0.0407 Debye Point Group
 |
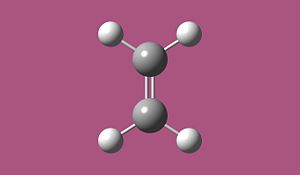 |
cis-butadiene
 |
 |
ethylene
 |
 |
Optimisation and Analysis of Transistion State
The Transition State was modelled using GaussView and optimised. A frequency calculation was also carried out in order to confirm the transition state had reached a minima. An imaginary frequency at -956cm-1 confirms this minima and is shown below. This frequency corresponds to the forming of the 2 new σ bonds. The next lowest frequency is at 147cm-1 which corresponds to the rocking motion of the ethylene hydrogens.
 |
 |
