Rep:Physicalsg
Module 3: Transition States and Reactivity
Objectives
In module 1 relative energies of conformers were investigated. In this module we can move on to investigate how reactions take place i.e. bonds forming and bonds breaking. This can be done, using molecular orbital methods, numerically solving the Schrodinger equation to find transistion structures on the local shape of a potential energy surface . For this module 3 different reactions will be investigated; the Cope Rearrangement of 1,5-hexadiene and the Diels-Alder Cycloadditions of cis-butadiene with ethylene and cyclohexa-1,3-diene with with maleic anhydride.
The Cope Rearrangement Tutorial
In the following exercise computational methods will be used in order to investigate the [3,3]-sigmatropic cope rearrangement of 1,5-hexadiene. The reaction obeys the 4n+2 rule, proceeds thermally and as such involves a Hückel Transition State.
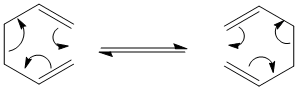
Optimisation of Reactants and Produtcs
1,5-hexadiene can exist in either an anti or gauche conformation. The optimised structures of the reactants and products need to be determined before any further investigation into the transition state structures. Therefore the anti and gauche conformers were visualised using GaussView 5.0 and optimised using the HF/3-21G method and their relative energies recorded.
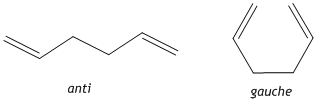
The anti conformer was found to have an energy of -231.69253528a.u and the gauche conformer was found to have an energy of -231.69266118a.u. With an energy difference of 0.3308 kJ/mol between the 2 conformers it has been found that the gauche conformer is the more stable and this can be explained by the CH-π interaction, i.e. a favourable interaction between the σ* orbital of the vinyl proton and the π orbital of C=C bond of the alkene. In fact, the energy difference found here is actually smaller than would be expected from the effect of the CH-π interaction, however the HF method does not consider these electron-interactions accurately.[1] The energies and symmetries [Ci]of the 2 conformers agree with that found for anti2 and gauche3 found in Appendix 2. The anti2 structure was then optimised again using a higher level basis set B3LYP/6-31G* and using this basis set the energy of the molecule was found to be -234.61170997a.u in agreement with the information in Appendix 2 i.e. using a larger basis set locates a lower energy, more stable minimum.[2] The C-C, C=C bond lengths are in agreement with literature values at 1.54Å and 1.34Å respectively.[3]
 |
 |
 |
There is a significant difference in computed torsion angles in using the low level basis set as opposed to the high level basis set.
Torsion Angles (high level):
[C 1,2,3,4] 118.54991 degrees
[C 2,3,4,5] 180.0 degrees
[C 3,4,5,6] 118.54991 degrees
Torsion Angles (low level):
[C 1,2,3,4] 114.66878 degrees
[C 2,3,4,5] 180.0 degrees
[C 3,4,5,6] 114.66878 degrees
Vibrational analysis of anti2
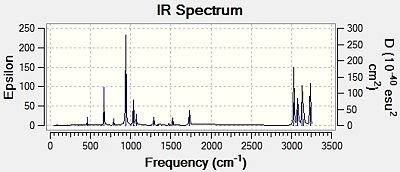
Using a frequency analysis it was possible to confirm whether the anti2 had in fact been optimised. The results of this analysis show all modes are positive and real confirming that this optimisation was successful. The frequency calculation was run using the higher level basis set,B3LYP/6-31G*. Thermochemical data obtained from the output log of the frequency calculation confirms that all net forces and displacements have fully converged;
Thermochemical Data Obtained from output file [B3LYP/6-31G*]:
sum of electronic and zero-point Energies= -234.469203, sum of electronic and thermal Energies= -234.461856, sum of electronic and thermal Enthalpies= -234.460912, sum of electronic and thermal Free Energies= -234.500777.
Frequency analysis was also run using the lower level basis set [HF/3-21G], necessary later in report for determination of activation energies.
Thermochemical Data Obtained from output file [HF/3-21G]:
Sum of electronic and zero-point Energies= -231.539539 Sum of electronic and thermal Energies= -231.532565 Sum of electronic and thermal Enthalpies= -231.531621 Sum of electronic and thermal Free Energies= -231.570916
Optimising the Chair and Boat Transistion Structures
The Cope Rearrangement will proceed via a Chair or Boat shaped transition state. In the next set of calculations the transition states will be analysed in detail. To begin with, a CH2CHCH2 allyl fragment was visualised in GaussView i.e. half of each transition state and optimised using the low level basis set HF/3-21G. These optimised fragments could then be used to create a guess structure of both transition states.
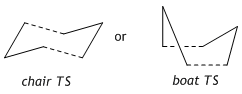
Chair Transtion Structure
In order to create a 'guess' of the Chair TS it was necessary to paste the previously created allyl fragment twice and orientate it to resemble the Chair structure. Firstly the chair TS was optimised to a TS (Berny), calculating the force constant once. The distance between terminal Cs had been set to 2.2Å as this method is sensitive to the input structure and as such will not work accurately if the guessed transition structure is not relatively close to that of the actual structure. Since the structure was already know this method produced good results in this case.
The optimised C-C [terminal] bond distances were found to be 2.02055Å in the optimised chair TS. A frequency calculation was also carried out which confirmed the structure was optimised to a transition state with one imaginary frequency at -817.9cm-1. This frequency corresponds to the breaking/forming of the new bond in the Cope Rearrangement. The chair conformation was then optimised again, using the Frozen Coordinate method. As before, the 2 allyl fragments were orientated to resemble the chair structure and the distance between the terminal Cs fixed or "frozen" to 2.2Å with the rest of the structure then being optimised. A second optimisation of the structure then involved this distance being relaxed. Again, a frequency analysis confirmed the TS had reached a minimum with an imaginary frequency at -818cm-1.
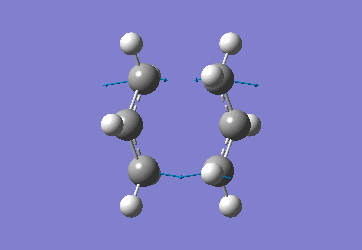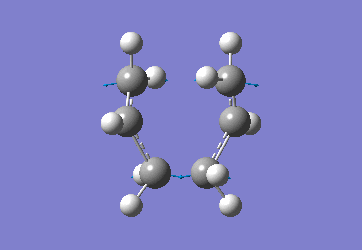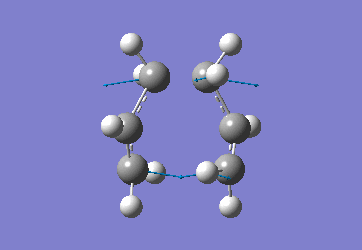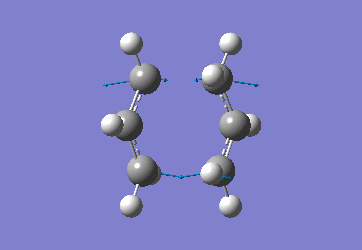 |
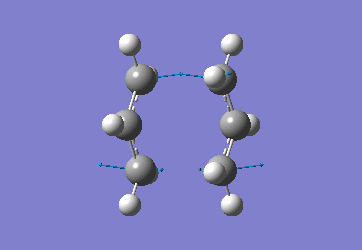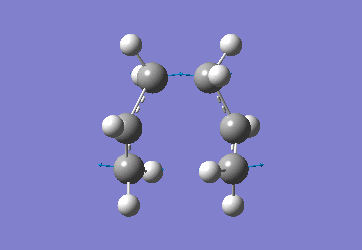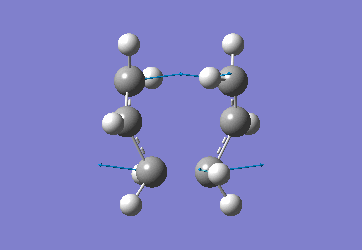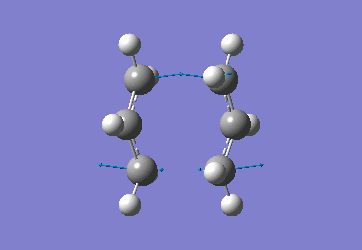 |
Boat Transition Structure
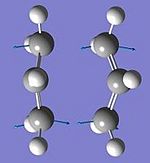
The QST2 method was used in order to optimise the Boat Transition Structure. In order to optimise using this method, the reactant and product must be input and the TS will be intrapolated between the 2 points. Firstly, the reactant and product were numbered according to the numbering if the reactant rearranges. This method did not produce successful results at the TS was not sufficiently accurate. This failure is as a result of the method not taking into account possible rotations around the central C-C bond. Some alterations were therefore made to the structure i.e. the C-C-C-C dihedral angle was set to 0 degrees and the inner C2-C3-C4 and C3-C4-C5 angles were set to 100 degrees. With these alterations the optimisation was then carried out successfully giving a final energy of -231.602802a.u for the boat TS. One imaginary frequency at 840cm-1 confirms the optimisation was successful.
Intrinsic Reaction Coordinate
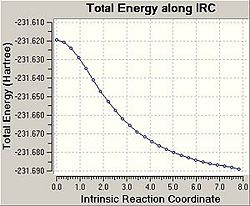
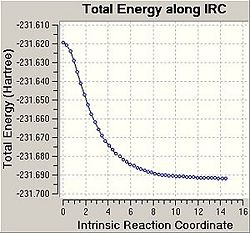
Using the Intrinsic Reaction Coordinate function of GaussView it is possible to predict which conformers are formed from the transition states i.e. which reaction path will be taken. The IRC follows the minimum energy path from a transition structure down to its local minimum on a potential energy surface.
 |
 |
 |
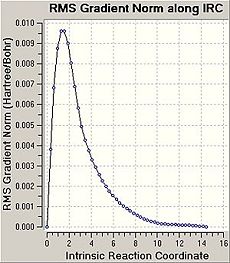 |
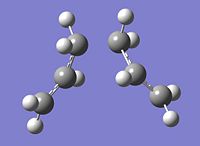
Firstly, the force constant was only calculated for the first step however this did not give accurate results. The graphs produced show the optimisation did not reach a minimum i.e. the graph has not plateaued. From these results it was clear that further calculations needed to be carried out on the final structures located by the IRC. The calculation was therefore repeated with the force constant being calculated at every step. In this case the graphs produced have plateaued and as such it is clear that a minimal energy structure has been reached for the chair transition state. A minimisation was then carried out on the chair transition structure and the final structure achieved is shown. The final energy was found to be -231.69167a.u which corresponds to the gauche2 conformer, as listed in Appendix 1.
Determining Activation Energies
Thermochemical data obtained from output file [all energies from output file in a.u]:
anti2
[HF/3-21G]: sum of electronic and zero-point Energies= -231.539539, sum of electronic and thermal Energies= -231.53256, sum of electronic and thermal Enthalpies = -231.531621, sum of electronic and thermal Free Energies= -231.570916.
[B3LYP/6-31G*]:sum of electronic and zero-point Energies= -234.469203, sum of electronic and thermal Energies= -234.461856, sum of electronic and thermal Enthalpies= -234.460912, sum of electronic and thermal Free Energies= -234.500777.
chair transition structure
[HF/3-21G]: electronic energy = -231.619322, sum of electronic and zero-point Energies= -231.466700, sum of electronic and thermal Enthalpies = -231.461340.
[B3LYP/6-31G*]:electronic energy = -234.556984, sum of electronic and zero-point Energies= -234.414931, sum of electronic and thermal Enthalpies = -234.409010
boat transition structure
[HF/3-21G]: electronic energy = -231.602802, sum of electronic and zero-point Energies= -231.450929, sum of electronic and thermal Enthalpies = -231.445300.
[B3LYP/6-31G*]:electronic energy = -234.543093, sum of electronic and zero-point Energies= -234.402342, sum of electronic and thermal Enthalpies = -234.396008
ACTIVATION ENERGIES
HF/3-21G
ΔE Chair @ 0K = 45.71kcal/mol, @ 298.15K = 44.69kcal/mol
ΔE Boat @ 0K = 55.60kcal/mol, @ 298.15K = 54.76kcal/mol
B3LYP/6-31G*
ΔE Chair@ 0K = 34.06kcal/mol, @ 298.15K = 33.17kcal/mol
ΔE Boat@ 0K = 41.96kcal/mol, @ 298.15K = 41.33kcal/mol
The Diels-Alder Cycloaddition
In the following exercise the reactivity and mechanism of the Diels-Alder cycloadditions of cis-butadiene with ethylene and cyclohexa-1,3-diene with maleic anhydride will be investigated i.e. the effect of the presence of substituents on stabilising the regiochemistry of the Diels-Alder product. The reactions will be explored using GaussView to visualise reactants and products along with Gaussian optimisation, frequency and MO calculations. The Diels-Alder reaction proceeds via a concerted mechanism in which 2 or more σ bonds are formed or broken between the termini of 2 or more π-conjugated systems.
Optimisation and MO/Frequency Analysis of cis-butadiene and ethylene
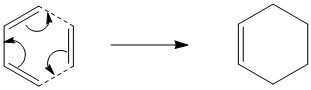
The Diels-Alder cycloaddition of cis-butadiene with ethylene proceeds via a 4n+2 [thermal] Hűckel transition state and as such takes place suprafacially. The MOs of the reactants and products and the resulting transition state were computed to assess if the reaction proceeds via a concerted stereospecific fashion or not.
The reactants were visualised using GaussView and optimisation calculations carried out using the semi-empirical AM1 method. The total energy for the cis-butadiene molecule was found to be 0.04616719 a.u and for ethylene the energy was found to be 0.02619027a.u.
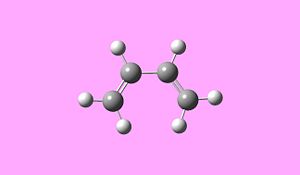 |
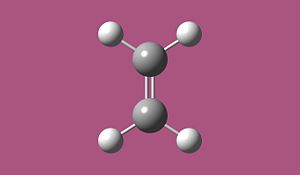 |
MO Analysis of cis-butadiene
 |
 |
MO Analysis of ethylene
 |
 |
From the computed MOs above we see that, as expected, the MOs with the most out-of-phase interactions will be of the highest energy i.e. the LUMO of ethylene is highest in energy while the MO with the most bonding interaction, the HOMO of ethylene is at the lowest energy. It should also be noted that the LUMO of cis-butadiene is almost anti-bonding i.e. at 0 a.u. The symmetry of the computed MOs was determined with respect to the σv plane. Since only MOs of the same symmetry can interact, it can be seen that the HOMO of cis-butadiene will interact with the LUMO of ethylene as they are both antisymmetric and vice versa.
The computed bond lengths of reactants and transition structures have been found and as such can be compared with literature values/typical bond lengths. For the starting materials the optimised structure of ethylene has a C=C bond length of 1.33Å while cis-butadiene has a C=C bond length of 1.34Å which agrees with the typical value of 1.341.54Å for the sp2 C=C bond length. When modelling the transition state the distance of the newly forming C-C single bonds were set to 2.2Å. This value did not change a lot in the optimisation of the transition structure, it is 2.1Å in the final structure. This bond length is a lot longer than the typical value of a sp3 C-C bond length [1.54Å], this is to be expected given that the bond is only partially formed.
The VdW radius of a Carbon atom is 1.71Å and given that the distance between the two terminal Cs is less than 2 times this distance and as such it can be confirmed that a bond is formed, although as this is a transition state the bond is obviously not fully formed yet. Since the bond distances are exactly the same, it can be said that bond formation is simultaneous, this observation can be confirmed by the number of imaginary frequencies observed in the spectrum, relating to bond forming vibrations i.e. one frequency suggests the 2 bonds are being formed simultaneously.
Optimisation and MO/Frequency Analysis of Transistion State
The Transition State of this reaction is an envelope shape structure which maximises overlap between the ethylene π orbitals and the conjugated π-system of cis-butadiene. The transition struture was modelled using GaussView and a Opt+Freq calculation carried out using the semi-empirical AM1 method. The optimisation was set to a TS (Berny) with the additional keywords "Opt=NoEigen". The 2 terminal C-C distances [between the 2 systems] was set to 2.1Å. The frequency calculation was included in order to confirm the transition state had reached a minima. An imaginary frequency at -956cm-1 confirms this minima and is shown below. This frequency corresponds to the forming of the 2 new σ bonds. The next lowest frequency is at 147cm-1 which corresponds to the rocking motion of the ethylene hydrogens. There is no bond breaking/forming related to this frequency which indicates ethylene is not involved in the reaction pathway.


FMOs of the Transition State
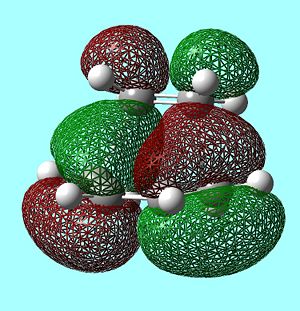 |
 |
As can be seen above, the HOMO of the TS is antisymmetric and has therefore been formed from the HOMO of cis-butadiene and the LUMO of ethylene as they are both antisymmetric. In the same way, the LUMO of the TS is symmetric and has been formed from the LUMO of cis-butadiene and the HOMO of ethylene.
The Regioselectivity of the Diels-Alder Cycloaddition: cyclohexa-1,3-diene with maleic anhydride
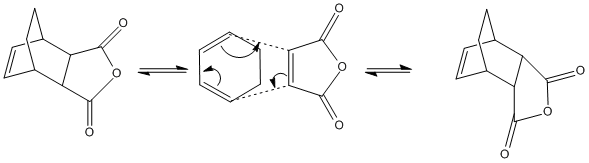
The reaction scheme shows the stereoselective Diels-Alder cycloaddition of cyclohexa-1,3-diene with maleic anhydride. Again, this reaction follows the obeys the 4n+2 rule, proceeds thermally and as such will take place via a Hückel Transition State with all components reacting suprafacially. It is already known that the reaction is kinetically controlled with the endo-adduct being the major product, given this, it is the energy of the transition states which need to be studied. Since the endo-product is the major product the transition state of the exo-adduct must be at a higher energy.
Optimisation and Frequency Analysis of Transition State
The starting materials were visualized using GaussView and arranged to make a good guess of the transition states of both the endo and the exo adduct. The distance between the two terminal C was set to 2.2Å. An Opt+Freq calculation was then carried out, again using the semi-empirical AM1 method with the optimisation set to a TS (Berny) and the additional keywords, Opt=NoEigen and the calculate force constant set to always.
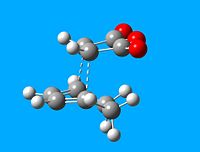 |
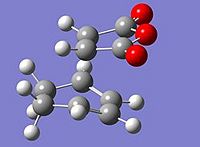 |
The optimised exo TS was found to have an energy of -0.05041985a.u while the optimised endo TS was found to have an energy of -0.05150480a.u. The difference in energy can be partly attributed to steric reasons, i.e. the exo transition structure experiences steric clash between the bridgehead of the cyclohexadiene ring and the 3 O atoms of the maleic anhydride. The endo structure avoids this clash as the these two components are on opposite ends.
A frequency analysis was carried out in order to confirm the transition states had been optimised. The presence of an imaginary frequency in both the spectrum of the endoadduct and exo adduct suggests they have been optimised, [-806cm-1 and -812cm-1 respectively].
 |
 |
MO Analysis of Reactants and Transition States
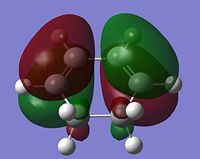 |
 |
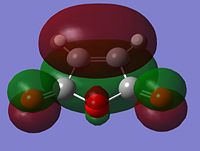 |
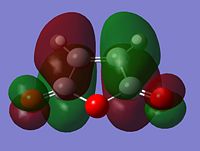 |
 |
 |
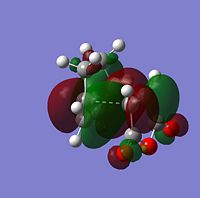 |
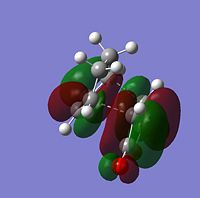 |
From looking at the symmery found for each of the MOs, it is clear that the HOMO of cyclohexadiene combines with the LUMO of maleic anhydride to form the endo and exo transition states, given that they are both antisymmetric and both transition states are antisymmetric. Further to the steric reasons mentioned in the previous section, the MOs of the endo and exo transition structures can be used to explain why the endo transition structure is of a lower energy. The stabilisation of the endo transition structure has been accounted to secondary orbital overlap. This orbital interactions between the diene and the dienophile in this case interaction between the π-orbitals of the C=O component of maleic anhydride and the π-orbitals of the dienophile [cyclohexadiene]. The secondary orbital interactions do not result in the formation of a bond, however primary orbital overlaps/interactions do. [4]
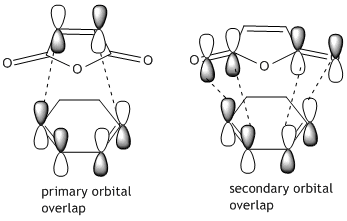
In the exo structure the carbonyl components of the maleic anhydride are pointing in the opposite direction and as such no stabilising secondary orbital interaction can take place. It is also important to note that the distance of the newly forming C-C bonds in the endo structure is slightly smaller, 2.162Å compared to 2.169Å for the exo structure.
References
- ↑ Hirota et al; "Intramolecular CH–π interaction: Substituent effect as a probe for hydrogen bond-like character," Journal of Physical Organic Chemistry, Vol. 13, Issue 10, p.620–623,2000.
- ↑ Module 3
- ↑ Hirota et al; "Intramolecular CH–π interaction: Substituent effect as a probe for hydrogen bond-like character," Journal of Physical Organic Chemistry, Vol. 13, Issue 10, p.620–623,2000.
- ↑ B.S. Jursic; "A Density Functional Theory Study of Secondary Orbital Overlap in Endo Cycloaddition Reactions," J. Org. Chem. 1997, 62, 3046-3048.
