Rep:Physical:whoisthedaddy
The aim of this investigation is to use a variety of calculation techniques in order to study the transition structures of two different reactions.
Investigation into the Cope Rearrangement
Reactants
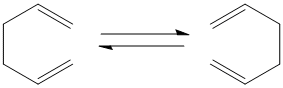
In order to explore the Cope reaction shown in the diagram to the left, a variety of conformers must be analysed. Primarily conformers of the reactants will be investigated followed by transition states. The first of which being the anti and gauche 1,5 cyclohexadiene reactants, the default method and basis set HF and 321G were used and the point groups and energies are shown in the table below. By comparing the energies and point groups of the two optimised conformers with Appendix 1 it was confirmed that they are the Gauche(1) and Trans(2) conformers.
| Point Group | Energy (Hartrees) Method = HF/3-21G | Energy (Hartrees) Method = B3LYP/6-31G |
|---|---|---|
| Ci | -231.68539619 | -233.32932706 |
| Point Group | Energy (Hartrees) |
|---|---|
| C2 | -231.67932505 |
It was expected that the Trans conformer would be more stable and this is infact the case. The steric interactions present in the Gauche conformers tend to destabillise them. However the lowest energy conformer found is actually the Gauche(3) conformation showm below. The reason that this conformer is most stable is the Gauche effect. The Gauche effect involes the donation of electron density from the C-H σ orbital into the п* orbital of the C=C double bond. This effect weakens the C=C bond but stabilises the molecule as a whole. The presence of the Gauche effect in the Guache(3) conformation could be rationalised by analysing the molecular orbitals of the molecule, however this would be beyond the scope of this investigation.
| Point Group | Energy (Hartrees) |
|---|---|
| C1 | -231.69132505 |

The Anti(2) structure with Ci symmetry will now be optimised using the more accurate method BY3LP and 6-31G basis set. As expected the total energy of the conformer when optimized under this method is lower than that with the less accurate method, however this is not a reliable conlcusion as energies obtained by using different methods are not neccessarily comparable. The C=C double bonds shortened slightly with the BY3LP method optimisation and the single bonds lengthened slightly, these results are shown in the table below.
| Bond | Length BY3LP (A) | Length HF (A) |
|---|---|---|
| C1=C2 | 1.33132 | 1.31593 |
| C2-C3 | 1.52291 | 1.51972 |
| C3-C4 | 1.54704 | 1.54258 |
The frequency analysis of this molecule was then calculated to ensure a minimum had been obtained. The following energy values were gained from the subsequent log file.
| Type | Energy (Hartrees) |
|---|---|
| Sum of electronic and zero-point Energies | -233.186831 |
| Sum of electronic and thermal Energies | -233.180886 |
| Sum of electronic and thermal Enthalpies | -233.179942 |
| Sum of electronic and thermal Free Energies | -233.216489 |
Transition State
The investigation will now move onto the chair and boat transition states and will optimise both of these with three different methods. The first of these involves computing the force constants before the optimisation, the second will use a redundant force constant editor and the third will use QST2. All these calculations will proceed using the HF method and the standard 3-21G basis set.
Chair Optimisation
The chair structures shown below was optimised using the first two methods described above.For these optimisations a guess of for the chair transition state was made using two molecules of propadiene. The first optimisation proceded as a TS-Berry method, whilst the second method froze the two terminal carbon bond lengths to 2.2A before the optimisation.
| Property | 1 | 2 |
|---|---|---|
| Energy (Hartrees) | -231.61932238 | -231.61520208 |
| Terminal C-C bond (A) | 2.01978 | 2.19920 |
The imaginary vibration for both optimisations occured at a frequency of -818cm-1 and when animated showed the concerted formation and breaking of bonds involved in an electrocyclic reaction. As expected the different style of optimisiation gave little difference in energy, however the first optimisation gave shorter terminal C-C bond lengths.
Boat Optimisation
Two of the Anti(2) molecules from earlier in the investgation were modified to give the product and reactant of the Cope Rearrangement, they were then optimised using the 2-QST method with a HF-3-21G basis set. However this calulation failed as this method requires the products and reactants to look simillar to the transition state. The two molecules were then modified further to replicate the T.S, they were then optimised using T 2-QST method again to give the structure shown to the left.

The imaginary frequency of this transition state occured at -838cm-1 therefore proving that it was an actual T.S that was found as the vibration corresponded to the synchronised breaking and formation of the two bonds in the Cope rearrangement.
In conclusion the 2-QST method is slightly more labourious in the fatc that the reactants and products need to look like the T.S in order for the optimisation to work.
The slightly more complex B3YLP method and 6-31G basis set was then used to optimise the chair transition state further in order to obtain the actviation energy at 0K and 298K for the reaction.
Sum of electronic and zero-point Energies= -234.455705
Sum of electronic and thermal Energies= -234.447943
Sum of electronic and thermal Enthalpies= -234.350999
Sum of electronic and thermal Free Energies= -234.389080
The activation energy at 0K is the (Sum of electronic and zero-point Energies) - (Actual Energy).
(-234.455705)-(-234.50152962) = 28.755389334kcal/mol
The activation energy at 298K is the (Sum of electronic and thermal Energies) - (Actual Energy).
(-234.447943)-(-234.50152962) = 33.626125187kcal/mol
These values are in agreement with the literature vaules reported in the lab script.
Transition State Analysis
When viewing the different possible transition states it is hard to tell which one the reaction actually proceeds with. In order to do this the Intrinsic Reaction Coordinate (IRC) method must be used. This calculation proceeds with a T.S input file and measures the gradient across the potential energy surface The chair transition state shown above was then run under an IRC calculation in the forwards direction with 200 steps to ensure a minima was found, this was done to acheive an activation energy for the process and to analyse which of the 1.5 hexadiene conformers the reaction actually proceeds via.

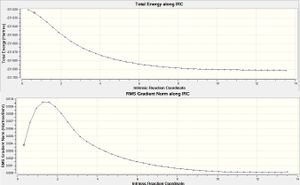
The structure obatined from the IRC calculation replicates the Gauche(2) conformer from the appendix in the lab script. The output from this calculation also has a C2 symmetry and an energy of -231.6882 Hartrees which correlates with -231.6916Hartrees for the Gauche(2) conformer therefore confirming that Cope Rearrangement proceeds via this conformer.
Diels Alder Analysis
Butadiene and Ethyene
This classic pericyclic reaction can only proceed if there is significant overlap between the HOMO of a Diene and the LUMO of a dieneophile. This experiment will show this with two different examples, the first of which being the reaction between ethylene and cis-butadiene..
Cis-butadiene was modelled in Gaussian and optimised with the basic HF-321G level of theory, its orbitals were then modelled and shown below.
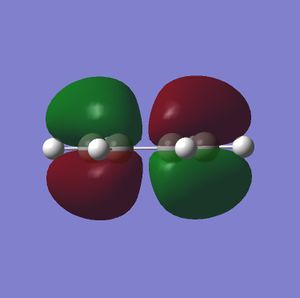

It can be seen clearly from these images that the HOMO is antisymmetric to the plane where as the LUMO is symmetric with the mirror plane of the molecule. Cis-butadiene can then only react if ethylene has an antisymmetric LUMO and this can be seen when analysing the HOMO and LUMO of Ethylene shown below.


The LUMO of Ethylene is antisymetric to the plane of symmetry in the molecule therefore this can interact with the HOMO of Cis-butadiene to give the T.S shown below.

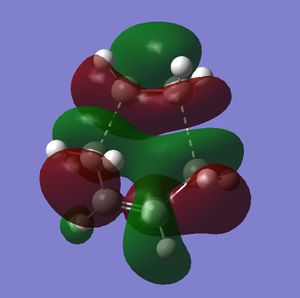
The transition state was then subjected to frequency analysis and the imaginary frequency at -527cm-1 is shown below, this vibration involves the synchronous formation of the two new C-C bonds proving that this is infact the transition state for this particular diels alder reaction. When viewing the HOMO of the T.S it is clear to see that it is assymetric withe the plane of symmetry of the molecule, this proves that the HOMO-LUMO interaction between ethylene and cis-butadiene is asymmetric.
The partially formed C-C bond lengths in the T.S are 2.267A and 2.356A and its energy is -231.476Hartrees. The partially formed C-C bonds are substantially longer than the literature value for sp3 C-C bond is 154pm . This increase in length suggests a decrease in the bond order of the C-C bond as there is only a small interaction between the atoms. The Van der Waal radius of C is 1.7A2, this value multiplied by two is 3.4A, which is greater than the measured bond lengths. Therefore there must be another attractive force between the two atoms as the bond distance is shorter than 3.4A, this frce is the formation of the C-C bond.
Cyclohexadiene and Maleic Anhydride
In order to extend this investigation the reaction between Maleic anhydride and 1,3 cyclohexadiene will be used to analyse the regioselectivity of the Diels Alder reaction. A TS Berny calculation was run at the HF/3-21G level of theory for both the Exo and Endo transition states of the reaction.
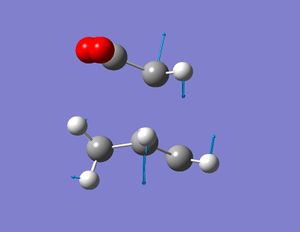

This table compares the imaginary frequencies and energies of the two isomers. The two images show the imaginary frequecies relating synchronous formation of the two C-C bonds in the Diels Alder reactions, confirming that the correct transitions states have been obtained.
| Property | Exo | Endo |
|---|---|---|
| Energy (Hartrees) | -605.60359125 | -605.61036823 |
| Imaginary Frequency (cm-1) | -647.45 | 643.52 |


The HOMO is antisymmetric as opposed to the LUMO which is symmetric to the mirror plane of the molecule.


As expected it is the opposite case for maleic anhydride as the HOMO is symmetric and the LUMO is antisymmetric. Therefore this reaction can proceed with orbital interactions between the antisymmetric HOMO of 1,3 cyclohexadiene and the antisymmetric LUMO of maleic anhydride. The reaction is most likely to proceed in this fashion as maleic anhydride is an electron poor dienophile so will have a low lying LUMO increasing the ease of interaction with the HOMO of the di-ene.
The Endo transition state has a lower energy than the Exo T.S, therefore kinetically the Endo isomer is favoured due to a smaller activation energy. The explanation for this being the secondary orbital overlap1 also favours the endo isomer as shown in the diagram below, this is the favourable overlap between orbitals not directly involved in the bonding during the reaction. It can be seen that the endo isomer experiences a greater secondary orbital effect making it kinetically more stable.

The Exo transition state is also destabilised by unfavourable steric ineractions between H atoms and the rest of anhydrous ring, these interactions are not present in the Endo isomer.
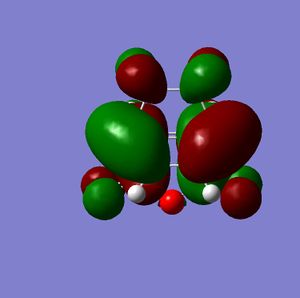



When viewing the MO's of the Endo transition state the interaction between the HOMO of 1,3 cyclohexadiene and he LUMO of maleic anhydride can clearly be seen.
References
1. M. A. Fox, R. Cardona, N. J. Kiwiet "J. Org. Chem." 1987, 52, 1469.
2. M. A. Fox, J. K. Whitesell, "Organische Chemie" 1949.
