Computational Labs: Module 3 - Transition State Chemistry

Introduction

This module focused on the structure of the transition state in the Cope Rearrangement and in Diels-Alder cycloadditions. Previously used molecular mechanics methodology could not be utilised here as it can only analyse molecular geometries, it cannot give any information about bond nature, electron distribution or make any calculations about bond breaking and forming. Instead, a new method of molecular orbital based computation will be employed, whereby the Schrodinger equation is numerically solved to give details about transition state structures and where they lie on the potential energy surface.

The Cope Rearrangement

Optimising the Reactants and Products

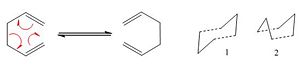
In this first exercise, the [3,3]-sigmatropic rearrangement of 1,5-hexadiene was studied. The aim was to locate the low energy minima and any transition structures on the reaction's potential energy surface, in order to comment on the mechanism. The scheme on the left shows the reaction and its two possible transition structures: the so-called boat and chair conformers. Gaussian software was used to model the reaction and initially the Hartree-Fock method with basis set 3-21G was employed.

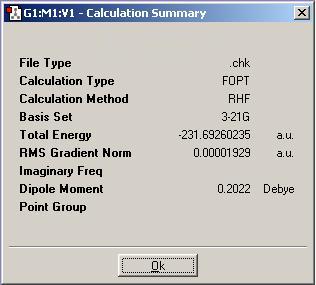
The first calculation was performed on 1,5-hexadiene in the anti conformation (model shown above). Optimising the molecule gave the results summary shown below (energy displayed in Hartrees). The symmetrize function was used in order to establish the point group of the molecule: C₂. This conformer is listed as 'anti 1' in Appendix 1.

The same procedure was also performed on 1,5-hexadiene in the gauche conformation, its point group was found to be: C₁. This conformer corresponds to 'gauche 3' in Appendix 1. A model of the molecule and results summary are shown below.

As can be seen from the summaries, the energies of both conformers are similar, only differing by: 0.00006 Hartrees. Initially the anti structure might be expected to be slightly lower in energy, for steric reasons. However, it is the gauche structure that is lowest in energy, this is due to the stabilisation seen from the "gauche effect". A process whereby electron density is donated from the σ_C-H to the п*_C=C orbital. Although this weakens the ene bond, it aids to lower the energy of the molecule overall. The energies of the optimised structures using this method are nearly a perfect match with the recorded energies for the anti 1 and gauche 3 conformers listed in Appendix 1. Relative to all other possible conformers, Appendix 1 confirms gauche 3 is the lowest energy structure, with anti 1 being the second lowest (relative energy: 0.04).

A final conformer was studied in this section, it corresponds to anti 2 in Appendix 1 and is an alternative anti orientation of 1,5-hexadiene - with C_i symmetry. It is drawn below with the results summary produced from a HF/3-21G calculation. Again the energy of the structure is a near perfect match to the value listed in Appendix 1.

This conformer was then subject to further calculation using a more accurate basis set: 6/31G* with B3LYP methodology. The results summary is shown below. The geometry of the B3LYP conformer did not change much at all from the less accurate HF model. On average, all of its C-C bonds elongated by ~0.001A - which given the inaccuracies of both calculations isnt a measurable difference. More notable is the difference in energy, the more accurate calculation displays a lower energy for the molecule. This is expected since a more in-depth optimisation has been performed.

In order to compare the optimised energies with experimental values, a frequency analysis of the anti 2 molecule was performed. This was also used to determine whether the structure was at an energy minimum. The analysis is summarised in the table below, showing a breakdown of the energies from the output .log file. All the frequencies in the output were positive, showing a minimum had been found.

Optimising the Chair Transition Structure

In order to create the chair transition structure, a propandiene fragment was modelled in Gaussian and was subject to HF/3-21G optimisation. Two of these fragments were then superimposed in a chair-like manor, 2.2A apart. This transition structure was then fully optimised using the TS Berny parameters, by calculating the force constants at the start of the calculation. A model of the transition structure is shown below.

A 'redundant coordinate editor' (RCE) method was then used to optimise the original structure as well. This method differed from TS-Berny by freezing the bond lengths between the terminal carbons of each fragment at 2.2A before the optimisation. The resultant molecule had almost identical geometry to the TS Berny optimised molecule, the corresponding C-C bond lengths only changing by a maximum of 0.01A. Also to note was the imaginary frequency of both molecules: -818 cm^-1, this is identical to the wavenumber quoted in the script. The vibration from this frequency is animated below, it shows the Cope rearrangement reaction because the arrow vectors indicate a concerted effort to break and make bonds on the termini of the two fragments.

Animated vibration of TS Berny optimisation, RCE optimisation provided almost identical animation.

Optimisation Comparison
Property	TS Berny	RCE
Energy/Hartrees	-231.61923477	-231.61863392

Optimising the Boat Transition Structure

In order to analyse the boat transition state for this reaction, the QST2 optimisation method had to be employed. This method required the input of the reactant and product molecule for it to deduce the transition state structure. Further to this, the calculation also required every atom to be correctly labelled so it knew exactly which atoms were taking part in the bond breaking and making. It was the previously studied anti 2 orientated molecule that was modified for this calculation, so it resembled a boat structure. The picture below on the left shows an incorrectly identified optimised transition structure, this was as a result of not entering the necessary information into the calculation as just detailed. The picture below on the right is the correctly identified boat transition structure, this calculation did run to completion. The evidence of this comes from the frequency analysis, showing an imaginary frequency vibration at -840 cm^-1, as expected in the script.

Transition Structure Analysis

To determine which conformers the Cope rearrangement actually proceeds by, the Intrinsic Reaction Coordinate (IRC) method was utilised. Here, the calculation took small geometric 'steps' along the gradient of the energy surface in order to determine a minimum energy pathway for the reaction. (This was done for the chair and boat structures.) Initially, the calculation was performed with 50 steps, the results however were incorrect - a minimum was not found. So the steps were increased to 200, and the following optimised structures were found.

The chair structure resembles the gauche 2 conformer and the boat structure matches the gauche 3 conformer, it must therefore be these two structures most found in the transition state of the Cope rearrangement.

Finally, an activation energy calculation was performed on the transition structures. Both structures were reoptimised under the B3LYP/6-31G* level of theory, from their original HF/3-21G structures. Frequency calculations were then run. The results are displayed in the table below, whilst the geometries of the two structures were similar, their activation energies differed considerably.

Activation Energy Data
Conformer	Calculated E_a/kcalmol^-1	Experimental E_a/kcalmol^-1
Chair	34.19	33.5±0.5
Boat	42.68	44.7±2.0

To conclude, the calculated energies are in very good agreement with the experimental values, suggesting the calculations have all been successful and are based on sound theory.

The Diels-Alder Cycloaddition

Cis-butadiene reacts with ethylene in a pericyclic [4s + 2s] cycloaddition reaction to form the cyclic ene shown in the scheme below. This part of the module was concerned with plotting the molecular orbitals of this reaction to understand the mechanistic rationale. I.e. if the HOMO and LUMO interactions are favourable the reaction will happen as described, if however they are not of matching symmetry or have poor overlap, this reaction will be forbidden.

Molecular Orbitals

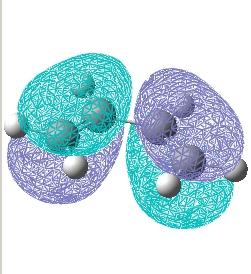
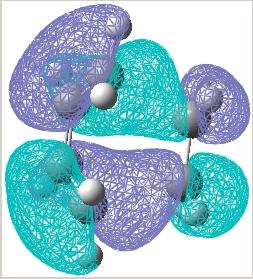
Firstly, butadiene and ethylene were modelled and optimised in Gaussian using the semi-empirical AM1 methodology. This level of theory was sufficient since only the HOMO and LUMO orbitals were being investigated. Orbital diagrams are shown below, they have the following symmetry:

Orbital Symmetry Data
Orbital	Symmetry
Butadiene HOMO	Antisymmetric
Butadiene LUMO	Symmetric
Ethylene HOMO	Symmetric
Ethylene LUMO	Antisymmetric

Transition State

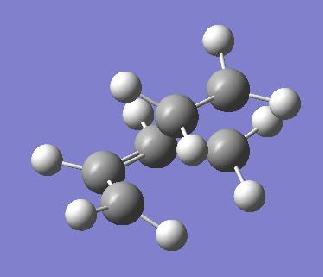
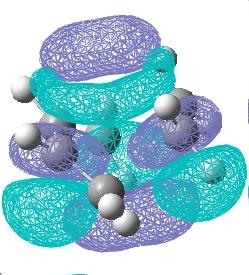
The transition state for this reaction can be thought of as an envelope structure - allowing π orbitals of both reactants to align and react. In this part of the module the transition structure was optimised using the same AM1 methodology (using frozen coordinates), as employed before. The optimisation structure is shown below, it yielded one imaginary frequency at -956 cm^-1 suggesting the desired bonds had been formed.

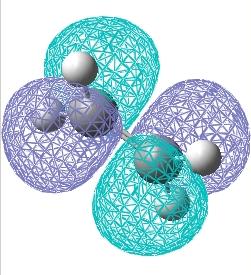
The HOMO and LUMO molecular orbitals were then plotted for the transition structure, these are shown below. It can be seen that the HOMO orbital is antisymmetric whilst the LUMO is symmetric. The reaction clearly works since the antisymmetric butadiene HOMO overlaps well with the antisymmetric ethylene LUMO to produce an antisymmetric transition structure.

Finally, by C-C bond length comparison it was deduced the transition structure was correct. The table below lists typical bond lengths for C-C bonds in the product cyclohexene, along with the C-C transition structure bond computed by Gaussian, and the VdW bond radius for comparison. What can be seen is the computed bond length is much longer than the ideal C-C bond in the product molecule suggesting the transition structure bonds are weaker and not fully formed. However, by being larger than the VdW value it signifies a chemical bond is present.

Cyclohexene bond lengths
Bond	Length/A
sp3 C-C	1.55
sp2 C=C	1.47
Transition C-C (from Gaussian)	2.19
C VdW Radius	1.70