Rep:Physical:indeed
The Cope Rearrangement
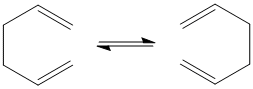
The Cope rearrangement is [3,3]-sigmatropic reaction involving six electrons, that results in an isomer of the reactant. The reaction scheme for the Cope rearrangement of 1,5-hexadiene is shown to the right. In this report, the reactants and products of this pericyclic reaction will be modelled in Gaussview and optimised by Gaussian in order to attempt to ascertain whether the reaction occurs by a concerted (or some other) mechanism. In order for results of the optimisations to be compared, the same calculation method and basis set must be used for all calculations.
Optimising the Reactants and Products
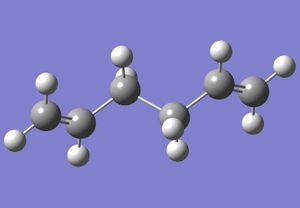
The reactant was modelled in Gaussview. An optimisation was carried out using the calculation method HF and the basis set 3-21G. The memory of the calculation was set to 250 MB, and the calculation was run. The 'anti' version of the molecule was obtained. This is shown below.
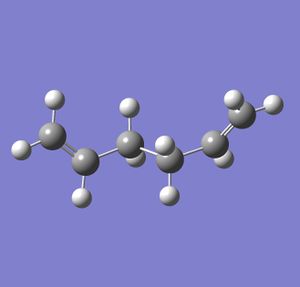
The structure was symmetrised, and gave a point group of C2. The dihedral angle between the hydrogen atoms on the two central carbons is 177.9 degrees, and the energy of the conformation is -231.69260235 Hartrees (note: although the accuracy of the calculated Hartree energies is not good enough to warrant a value quoted to this many decimal places, for a comparison to be made between conformations with only a small difference in energy, they must be quoted to the number of decimal places that Gaussian gives).
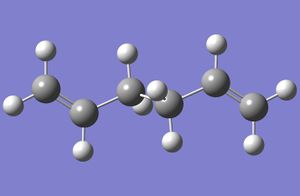
After this result, a 'gauche' conformation was modelled using the same calculation method and basis set, and the same memory limit of 250 MB. The result is shown below.
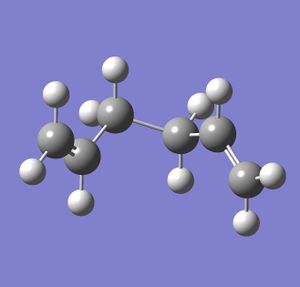
The structure was symmetrised, and gave a point group of C2. The dihedral angle between the hydrogen atoms on the two central carbons is 62.5 degrees, and the energy of the conformation is -231.69166702 Hartrees.
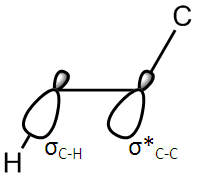
These conformers are not the only conformations of 1,5-hexadiene. Despite this, all conformers will either have an antiperiplanar or Gauche structure. Antiperiplanar molecules are genrally more stable due to steric effects, and so it would be fair to assume that one of the anti conformations is likely to be the most stable. However, the Gauche conformations in this molecule will benefit from the Gauche effect. This is when a favourable overlap occurs between the sigma orbital of a C-H bond and the sigma star of a C-R bond. R can be any group, but the nature of the group affects the strength of the trans effect. Here, it is between a C-H and C-C bond, which is a good enough overlap to make it likely that a Gauche conformation will be the most stable.
Comparing my calculated conformations with the Appendix table[1], it is the anti 1 and gauche 4 conformers that have been made. The lowest energy conformers are anti 1 and gauche 3. These are shown below (although anti 1 has already been shown above, it is shown below for clarity).
 |
 |
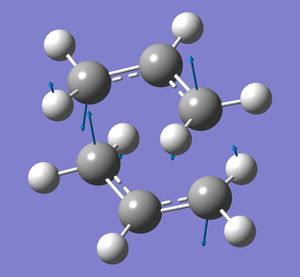
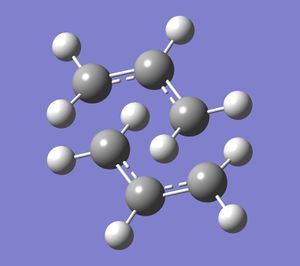
The anti 2 conformation, which has a symmetry of Ci, was calculated using the HF calculation method and 3-21G basis set. After this, it was re-calculated using the B3LYP calculation method and 3-21G basis set, and the total energies were compared. As seen in the results below, the more accurate B3LYP method results in a lowering of the energy by 4315.8 kJ/mol, with retention of the Ci point group. However there is little visible change in the molecule's conformation, showing that the difference in energy is mainly due to the change to a more accurate calculation method.
 |
 |
A frequency calculation was then run on the B3LYP-calculated conformation. All of the vibrations obtained from the calculation were positive, showing that a minimum had been reached correctly. The output file was then examined, and some thermochemical values were obtained, shown below.

Optimising the "Chair" and "Boat" Transition Structures
To understand whether the transition state in the Cope rearrangement is a 'chair' or 'boat' shape, both possible states must modelled and optimised.
The Chair Transition Structure
The chair transition state was made first. This was done by drawing and optimising an allyl fragment (CH2CHCH2). This was then copied into a new molecule window twice to make the initial, non-optimised chair structure:

The structure was deliberately drawn to be fairly similar to an expected chair transition state, which will greatly speed up calculations and stop Gaussian from reaching the wrong minimum for the molecule.
The Gaussian calculation was then carried out using an Opt+freq calculation for a TS (Berny). Force constants were calculated Once, and the keyword Opt=NoEigen was used. This resulted in an optimised structure with an imaginary vibration at -818 cm-1. This vibration corresponds to the rearrangement reaction - the breaking of one bond at one end of the allyl fragments, and the formation of a bond at the other end.
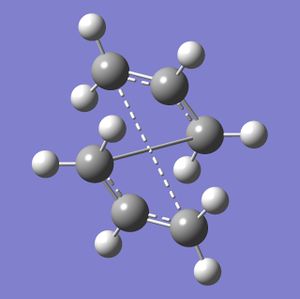
Next, a different type of optimisation was used: the frozen coordinate method. Using the same initial chair structure, the distance between the terminal ends of each allyl fragment were 'frozen' at 2.2 Angstrom. This means Gaussview optimises the rest of the molecule, but leaves these interactions, which will then be optimised afterwards in a seperate calculation (where the bonds are set to 'Derivative' rather than 'Freeze Coordinate'). The chair structure obtained after these two calculations is shown below.
The values obtained from the two methods are compared in the table, shown below.

As shown in the table, the two calculation methods produce very similar results, with little difference in the bond lengths and total energies.
The Boat Transition Structure
The boat structure was optimised using a different method - the QTS2 method. This uses the reactant and product to generate a transition state. However, in order for the job to run properly and the correct minimum to be reached, the input must be similar to the required output. The carbon and hydrogen atoms must therefore be labelled correctly, indicating to the program where in the molecule one bond is broken and where one is formed. The geometry of the reactant and product must also be similar to the transiton state.
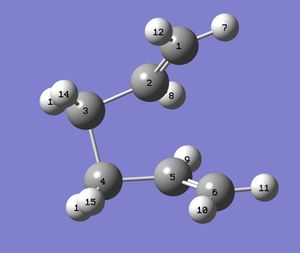 |
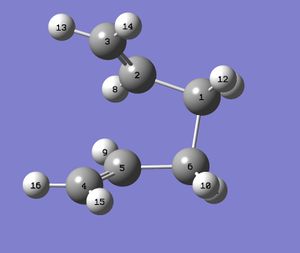 |
 |
The input file containing this information was submitted to Gaussian, and the desired boat transition structure was generated. The molecule contained an imaginary vibration at -840cm-1, which shows the rearrangement.

Next, an Intrinsic Reaction Coordinate (IRC) calculation was run. First, the number of points along the IRC were set to 50. However this did not give a minimum geometry. From this result there are several ways of reaching a minimum, and the methods and results used to do this are displayed below.
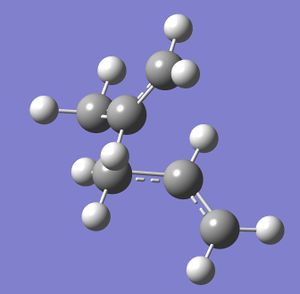 |
 |
 |
The transition state is getting closer to looking like the most stable (gauche 3) conformer. However, if the reaction is concerted, it can only get closer up to a certain point, otherwise one terminal carbon end will be too far from the other carbon end for a bond to be formed or broken. If the reaction is not concerted, then it is likely that the gauche conformation will be seen in one of the transition states of the reaction, as no such constraint will apply.
Activation Energies
To calculate the activation energies of the chair and boat conformations, a new minimisation has to be run using the B3LYP/6-31G level of theory. First, the lowest energy 1,5-hexadiene conformation was calculated using the new level of theory, giving a value of -234.61132934 Hartrees. The activation energy was then calculated. This is shown in the table below.
 |
 |
 |

The computational data obtained is in good agreement with the experimental data, showing the high level of accuracy of the B3LYP theory. Interestingly, the B3LYP molecules are in very similar conformations to the molecules computed by the HF method, although there is a large difference between the two sets of values.
The Diels Alder Cycloaddition
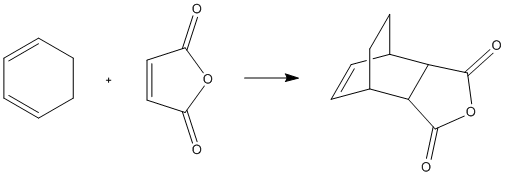
The Diels Alder reaction is a pericyclic cycloaddition. The reaction being investigated is between maleic anhydride and cyclohexa-1,3-diene, which reacts to give largely the endo product. This means that the exo product is higher in energy. This will be investigated computationally.
Modelling cis-Butadiene
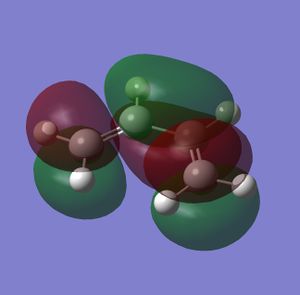
Before the full cycloaddition was modelled, cis-butadiene was optimised using the semi-empirical method AM1, and its orbitals were generated. This method is used because it is very fast and gives accurate enough results for analysis. Once a minimum is reached by the AM1 method, the moelcule can be more accurately optimised using other methods such as HF or B3LYP. However, with cis-butadiene there is no need for further optimisation as only the HOMO and LUMO orbitals are being investigated. These are shown below. From the plane of symmetry, it can be ascertained whether the orbitals are symmetric or anti-symmetric.
 |
 |
 |
Computing Transition State Geometry for a Prototype Reaction
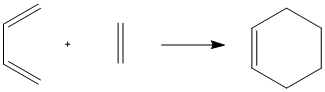
The reactants were modelled using the reaction scheme to the left in Gaussview. For the optimisation, the frozen coordinate method was used, using the AM1 calculation method. The Opt+Freq calculation generated a transition state with one imaginary vibration, showing that a minimum had been reached. This vibration corresponded to the bond breaking and bond forming in the reaction.
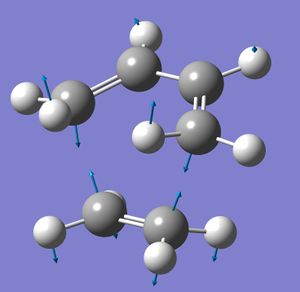
The MOs of the transtion state were modelled, and the HOMO and LUMO orbitals were investigated for their symmetry.
 |
 |
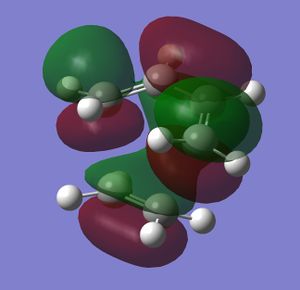 |
There is a large overlap between the orbitals of the butadiene and the ethene in the HOMO. This shows that in the transition state bonds are being formed between the two molecules, which agrees with the reaction scheme. The HOMO has been formed from two anti-symmetric orbitals - the antisymmetric butadiene HOMO, and the anti-symmetric ethene HOMO. As only antisymmetric promotions are allowed from the singlet ground state (symmetric promotions are forbidden), this is an allowed transition, and so the reaction will occur.
The transition state can be further investigated to check whether the correct bonds are being formed. This can be done by checking the bond lengths of the carbons in the transition state, and comparing them to sp3 and sp2 C-C bond lengths from the literature[2].

As the table shows, the C-C and C=C bond lengths in cyclohexadiene are very similar, showing that in the transition state the bonds are in a state of change (from double to single, or vice versa). The bond lengths are shorter than expected - you would expect them to be between single and double length (they are in fact very close to a sp C-C bond, which has a length of 137pm) - but this is probably due to the way Gaussian calculates stereoelectronics in transition states.
The Van der Waals radius of carbon is 170pm[3]. This means that, as the terminal carbon atoms are 210pm apart, there must be a chemical bond interaction between the two, as they are closer than their Van der Waals radius' allow for non-interactions.
The transiton state calculated is clearly the correct one, as the bond formation and breaking corresponds to the reaction scheme. The reaction is therefore concerted, and the formation of the two carbon bonds is synchronous.
Cycloaddition of Maleic Anhydride and Cylohexadiene
The endo and exo transition states of the diels-alder reaction between maleic anhydride and cyclohexadiene were modelled and optimised using the AM1 frozen coordinate method. After the transition states were optimised this way, the checkpoint files were re-optimised using the B3LYP/6-31g calculation to give the final optimised transition states. Both transition states had one imaginary vibration, showing that they had reached a minimum.
 |
 |
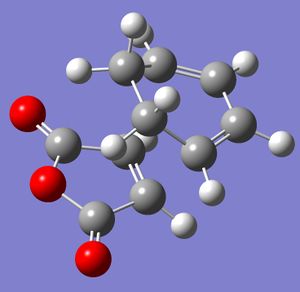 |
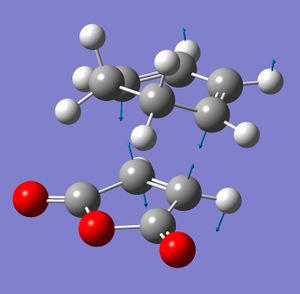 |
The terminal carbon distances and total energies are shown in the table below.

Both transition states have a terminal carbon distance of 2.3 Angstrom (230pm), which shows that there is an interaction occuring between the carbon atoms. The endo transition state, is, as predicted, more stable, and the energy difference between the two transition states is 10.73 kJ/mol.
The endo transition state is most likely more stable due to steric effects - the oxygen substituents on the maleic anhydride sterically clash with the diene in the exo transition state, whereas in the endo this does not occur due to the positioning of the maleic anhydride. However, these clashes do not affect the transition states too heavily, as the relative energy difference between them is quite low.
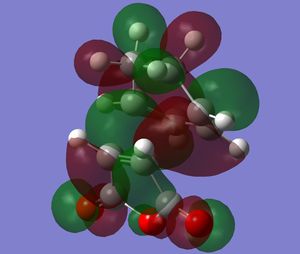
The transition states' MOs were then calculated. The HOMOs of the transition states are shown below. Looking at the plane of symmetry for the reaction, it is clear that both HOMOs are anti-symmetric.
 |
 |
 |
There is strong overlap in the orbitals in the two areas where a C-C bond is being formed, confirming that the correct transition states have been calculated.
According to the literature[4], the endo structure benefits more greatly from the secondary orbital overlap effect than the exo product - one of the reasons why the endo product is favoured. Looking at the HOMO orbitals of the two transition states, it is hard to see this effect in any real detail. However, the oxygen substituents' position in the endo structure seem be in a position to allow favourable overlap between the oxygen orbitals and orbitals on the diene. The exo does not benefit from this as its oxygen atoms are pointing out from the molecule and therefore cannot overlap any diene orbitals (they may slightly overlap with the two methyl groups on the diene, but their is a large distance between the methyls and oxygen atoms, so this is unlikely).
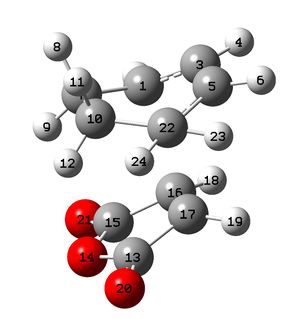
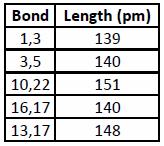
To further check whether the correct transition state had been made, the bond lengths were measured.
 |
 |
 |
 |
The C-C bond lengths are very similar to the values obtained from the cyclohexene transition state, again showing that the bonds are neither single nor double in the transition state. Additionally, the values are virtually identical when comparing the two transition states. This once again proves that the correct transition states were calculated.
These results are to a high standard, and agree with all the theory proposed. This means that the method and calculations chosen were very good, especially for a fast concerted reaction like the Diels-Alder. Apart from simply improving the detail of the calculation, there is little to be done that will increase the accuracy of the results. However, solvent effects were unaccounted for in the calculations, and these can greatly effect the selectivity of reactions (although it is understandable as to why they have been left out of the calculations, as accounting for solvent effects would cause a lot of additional time-consuming calculation time).
References
- ↑ http://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3#Appendix_1
- ↑ Fox, MA and JK Whitesell. Organische Chemie. 1994. Spektrum
- ↑ http://dx.doi.org/10.1021/j100785a001
- ↑ http://dx.doi.org/10.1021/jo00384a016
