Rep:Physical:Club banger
Module 3
The Conformations of 1,5 hexadiene
A selection of the low-energy conformations of 1,5 hexadiene were analysed computationally and their relative energies are given in the table below. The main variables in geometry between the different examples is the anti-periplanar or gauche nature of the 4 central carbon atoms and then the orientation of the alkene groups relative to each other. The method used for the calculations was Hartree Fock and the basis set was 3-21G.
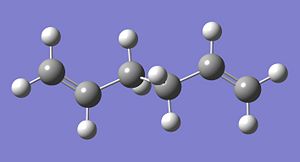
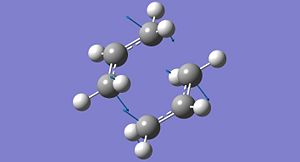
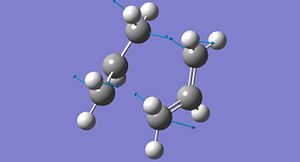
A particular conformer of the 1,5-hexadiene belongs to the Ci point group. This conformer is shown in its optimised form from both the HF/3-21G method (left) and the B3LYP/6-31G method. It can be seen that the difference in geometry between the two structures is minimal, despite the differences in basis set and the level of theory used.
Energy of the Ci conformation was -234.55965655 Hartree. ...kJ/mol higher than the optimal conformation.
Some thermochemical data was extracted from the calculation and is displayed below.
Sum of electronic and zero-point Energies= -234.416253 Sum of electronic and thermal Energies= -234.408952 Sum of electronic and thermal Enthalpies= -234.408008 Sum of electronic and thermal Free Energies= -234.447897
Optimising the Chair and Boat Transition Structures
The Cope rearrangement of 1,5-hexadiene is believed to be able to proceed via two possible transition states, one which resembles the 'boat' form of cyclohexane and one which resembles the 'chair' form. These two structures are essentially two C2H5 allyl fragments roughly 200pm apart. To study these transition structures the allyl fragments first had to be optimised within themselves and orientated to a reasonable estimation of the TS geometry.
The initial optimisations were done using the Hartree Fock method and the 3-21G basis set for the ally fragments, and for the transition state search.
The chair transition state was found using two different methods, the first was a single calculation which optimised the structure to a Berny TS. This required an initially good guess for the geometry of the TS and managed to optimise to the structure shown below.
The other method involved a preparative optimisation in which the geometry was constrained to keep the distance between the two fragments at a known distance. The redundant coordinate option allows a certain part of the molecule, be it atom position, bond length or an angle to be frozen whilst the rest of the molecule optimises around this. This allowed the two allyl fragments to be kept at a desired orientation whilst the optimisation took place. After this initial process, the constraints were released and the system was optimised again. The system proceeded to the expected TS and gave a negative freqeuncy almost identical to that in the other process. The advantages of using the redundant coordinates are not immediately obvious with this particular compound as the more direct method worked as well, but the using a constrained geometry can often allow an initally tricky optimisation to proceed to the desired minimum, when an unconstrained optimisation might proceed elsewhere.
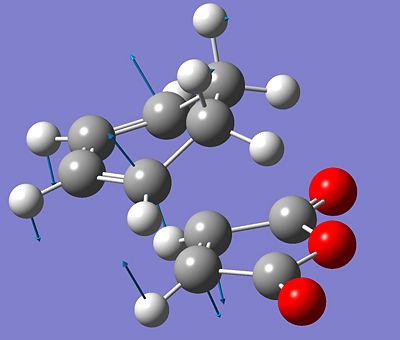
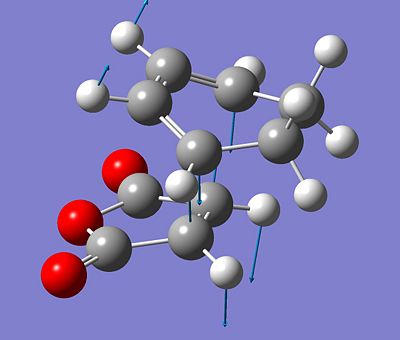
The two computed 'chair' transition states are shown below - the redundant coordinate is the right image. The arrow vectors signify the movement of the imaginary vibration given in the output from the frequency calculation. It shows the concerted formation and cleavage of C-C bonds on opposite sides of the transitional 6-membered ring. This gives evidence for the concerted reaction, which has no intermediates and just one transition state.
As mentioned above, the rearrangment is known to go via a different transiton state, one that resembles a 'boat' conformation of cyclohexane. The optimisation to this particular TS was more tricky and a different method needed to be employed. This method was QST2, a form of optimisation that takes two structures as an input and interpolates between the two to find a transition structure for their interconversion. As the product and reactant in the Cope rearrangement are identical the two structures put into the input file were exactly the same. The only difference being in the positions of the double bond. They appeared at the ends of each molecule, but to inform the computer that a rearrangement process had actually occured, the labelling of the atoms was adjusted.
The inital search for a transition state between these two structures was unsucessful. The geometries of the input molecules were expected to be too far from that of the expected transition structure and so some manipulations were made to make the initial molecules more similar the the TS and so give the search the equivalent of a smaller range of conformations to search in.
This manipulation eventually worked - after some problems with relative orientations of the hydrogens in the reactant and product state - and gave the desired transition state. This is shown below, with the vibration vectors again showing the imaginary frequency associated with the maximal stationary point.
After finding these transition states, the conformations which they connect need to be determined and this can be done by using the IRC method incorporated into gaussian. This follows the lowest energy path from the transition state to a minimal point and gives the low energy conformers which will interconvert via the geometry found.
The IRC calculations were run with 50 steps specified as the ending point. Both calculations ran for 24 steps and then terminated, it is not apparent why but the optimisations were run from this and gave favourable conformations. As the PE surface around the transition state should be symmetrical, the IRC was only computed in one direction. The computed conformations from the two different transition states are shown below. The conformation derived from the boat TS is the left image, and the conformation derived from the chair TS is the right image.
The activation energy for the rearrangement process could then be determined from these geometries, but to gain a more accurate insight the optimisations were redone using a better basis set and method, B3LYP/6-31G. It was seen that the geometies changed very little after optimisation to a higher level, but the energies did alter.
The energy differences between the starting conformations, and the transition states are tabulated below for the B3LYP methods.
| Energy Differences / kJ/mol | B3LYP/6-31G | Literature values / kcal/mol |
|---|---|---|
| Chair | 139 | 138.6-142.8 |
| Boat | 174 | 185.6-189.8 |
The calculated values are in good agreement with the reported literature values (on chemistry wiki). The chair transition state within the error range, but the boat transition state is a little lower than expected. Crucially the computational results agree with the relative activation energies particularly well.
Transition States of Diels Alder Reactions
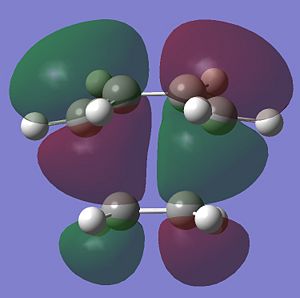
Quantum based computational methods were used to study the transition states of Diels Alder cycloadditions. The first study was on the most simple form of these diene-dienophile reactions, that of butadiene and ethylene. Butadiene was optimised using the semi-empirical method AM1. For Diels Alder reactions it is important to note the symmetry of the HOMO and LUMO with respect to the plane of the molecule and an axis in that plane.
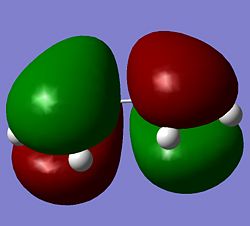
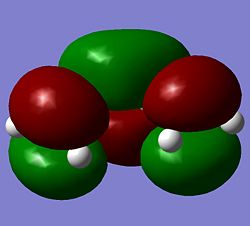
These images of the molecular orbitals show that the HOMO (left) is antisymmetric with respect to the plane as upon mirrorirng the carbons and orbitals map onto each other but the orbitals have a phase inversion. The rotational axis shows symmetry upon rotation through 180deg. The LUMO on the other hand is symmetric with respect to the plane and antisymmetric to the axis of rotation.
The butadiene molecule was then studied in an interaction with an ethylene molecule. The two fragments were orientated at an angle which allowed maximal pi orbital overlap. The planes of the molecules were perpendicular to each other and initally the distance between the two fragments was constrained to 2.2angstroms. This allowed a level of optimisation to be formed and gave a convenient stepping stone to a full optimisation to the transition state for the diels Alder reaction.
The optimised structure is shown here with the vibration vectors for the imaginary frequency. The vectors show the concerted formation of the two new sigma bonds, and shortening of the middle C-C bond in the butadiene. This is expected as the the mechanism is thought to be a concerted pericyclic whic forms a C=C double bond between the two original double bonds of the butadiene.
The image of the TS HOMO clearly shows the HOMO of the diene interacting with the LUMO of the ethylene. There is significant overlap between the pi-orbitals of the ethylene and the butadiene and this supports the formation of the bond. The two interacting fragment orbitals are of the same symmetry to the defined planes and roatational axis. They are symmetric with respect to the rotation and anti-symmetric with respect to the mirror plane. This is consistent with the symmetry constraints for orbital interaction in pericyclic reactions.
The forming C=C double bond, between C2 and C3, has a length of 1.40A. The 3 C=C bonds that are converting to sigma bonds all have a distance of 1.38A. These values are all intermediate between standard double and single C-C bond distances (1.32A and 1.52A). This would be expected in the transition state, as the reaction has not fully occured. The four intermediate values also gives evidence for the concerted nature of the reaction, as the bond being formed is occuring as the other bonds are being broken.
The new C-C sigma bonds being formed are at a distance of 2.12A. The reported Van der Waals radii for carbon is 1.70A[3]. This means that the two carbons would normally come no closer than 3.4A. The fact that they are at a separation much shorter than this implies that the interactions between the two atoms are not just Van der Waals forces (intermolecular) but that a chemical bond is likely forming, as electron density builds up between the two atoms.
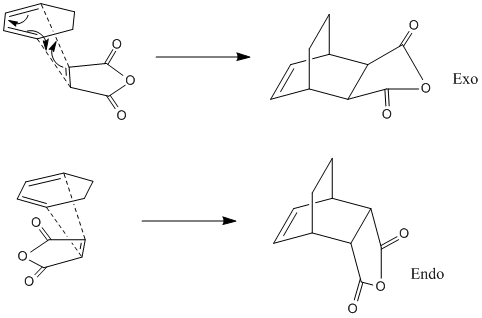
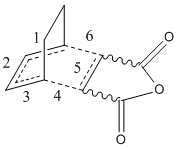
To build on this study of butadiene and ethylene, another diene and dienophile reaction was studied. Maleic anhydride and 1,3cyclohexadiene were the reactants, and this reaction was also picked to study the regioselectivity of such reactions. The isomers arise from the orientation of the reactants as they come together for the pericyclic reaction. The outcome can either be the exo or endo isomer. These two isomers formations are shown below.
The aim of the computation was to generate and distinguish the two transition states for the formation of the two isomers. This was achieved through the use of a semi-empirical method AM1. This allowed a good orbital approximation to be made before further optimisations were run as the basis set allows for a quantum analysis as well a classical view. Redundant coordinates were imposed to set a realistic orientation of the two reactant molecules. This was then optimised to a minimum, not a maximum. This gave a stable conformation to start from and reduced the chance of the transition state search getting 'lost' on the PE surface. Some problems were found with the reactant molecules just separating rather than coming together. The constrained minimum energy structure was then optimised to a transition state and this was then allowed to optimise fully. A frequency analysis was also run to confirm the stationary point found was a maximum. Both isomers were optimised by this method and gave 1 negative frequency each.
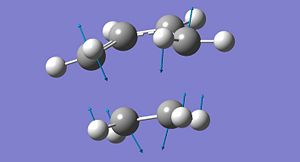
Images of the transition states are given below. The optimisation was run using the AM1 semi-empirical formula. The displacement vectors represent the movement of the atoms in the imaginary frequency. They show the concerted formation of the two sigma bonds between the pi-systems. Exo isomer is the left image, endo is the right.
The bond lengths of the newly formed six membered ring are tabulated below.#
| Bond | Exo | Endo |
|---|---|---|
| 1 | 1.39 | 1.39 |
| 2 | 1.40 | 1.39 |
| 3 | 1.39 | 1.39 |
| 4 | 2.17 | 2.16 |
| 5 | 1.41 | 1.40 |
| 6 | 2.17 | 2.16 |
It is interesting to see that the 4 C-C bonds that are either forming or losing a pi-interaction are almost all the same distance at 1.39/1.41. Common C-C single bond lengths is around 1.52A, and C=C is usually ~1.32A. These distances displayed are clearly intermediate between the two, and so all four must still retain some pi-character. The reaction is known to proceed in a concerted manner - hence finding just one transition state and no intermediate - so it is not suprising to see the rates of formation and cleavage of pi-bonds occur at the same rate.
The reaction is known to give the major product as the endo form, rather than the exo. It is also expected that the reaction is kinetically controlled, so the activation energy for formation of the exo isomer must be higher than that of the endo TS. Diels Alder reactions are known to be controlled heavily by orbital overlap, this primarily occurs between the pi-orbitals of the two reacting compounds, but some substituted reactants, such as the maleic anhydride can have secondary orbital effects, which work to stabilise the transition state, and so lower the activation barrier. These orbital effects must be balanced with steric interactions that occur in the transition state and so both effects will be analysed.
The steric interactions mainly occur between the anhydride group on the dienophile and the closest H2C-CH2 (HC=CH in endo form) of the diene. The hydrogens on the carbon come closest to the oxygens so are expected to have the biggest interaction. In the exo form the hydrogens pointion down toward the anhydride group are 2.69A from their respective carbonyl oxygens and 2.76A from the central oxygen. The endo form has much larger distances between the substituents at 3.31 from the carbonyl oxygens to the hydrogens on the carbon and 3.46 from the hydrogens to the central oxygen. This increase is distance is partly to do with the sp2 character in the carbons bringing the hydrogens into the plane of the C=C bond and away from the anhydride.
This data gives evidence for the endo transition state being more destabilised, as the atomic interactions will be stronger.
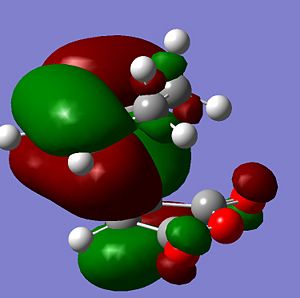
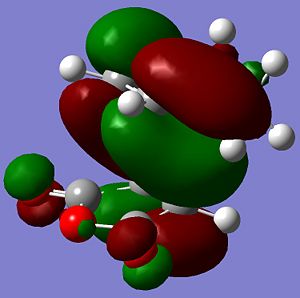
To study the orbital interactions in the transition state, the MOs of each form should be visualised. Below are images showing the HOMO of the exo form (left) and the endo form (right).
The endo effect occurs in Diels Alder reactions as the carbonyl substituents on the diene can interact favourably with the forming pi-bond at the back of the diene. This interaction can obviously only occur in the endo form, as in the exo the carbonyls are on the opposite side of the molecule compared to the forming C=C pi-bond.
The MOs above both show the HOMO of the diene, with one node between C2 and C3, interacting with the LUMO pi* of the dienophile. This interaction takes up much of the orbital space in the transition state HOMO.
For a favourable interaction to occur between orbitals, an occupied orbital should interact with an unoccupied one to yield a net reduction in energy of the occupied orbital. As the new pi-bond is formed at the back of the diene, it starts to gain electron density as electrons from the HOMO of the diene move to the LUMO - see orbitals of butadiene above. This orbital has significant pi-cloud above and below the C2-C3 bond, and this can interact with the large pi* lobes on the carbonyl carbons. This reduces the orbital being occupied and so reduces the energy of the transition state.
The endo form seems to be more stable in the transition state due to reduced steric interactions and increased favourable stereoelectronic interactions. The absolute energies of the two transition states show the endo form to be 2.9kJ/mol lower than the exo form at the AM1 level. Unfortunately, due to problems with optimisation, the B3LYP/6-31G calculations for the transition state were not completed. These would have given a much more accurate picture of the difference in energies and the geometries of the transition states but the AM1 also seems to be consistent with itself, as the less hindered and more electronically favourable endo gives a lower energy TS.
The main effect which has been ignored in these calculations is that of the solvent used. It is well documented[1],[2] that the solvent used in a Diels-Alder cycloaddition can greatly effect the ratio of products produced. The calculations are done on an isolated diene and dienophile so any possible solvent effects are ignored.
References
1. Pure & Appl. Chem. Vol 59, 1987 M. E. Paulatis, G. C. Alexander
2. J. Chem. Soc. Perkin Trans 2 1997 C Cativiela, JI Garcia, J Gil, RM Martinez
3. J Phys Chem. Vol 68, 1964 A Bondi