Rep:Physical:Alex
Module 3: Physical
The Cope Rearrangement

Molecular modelling can be used to determine, amongst other things, the transitions states and the low energy-minima associated with molecules taking part in a chemical reaction. When modelling a reaction this information can then be used to make predictions about the reaction mechanism. The cope rearrangement is an example of a [3,3]-sigmatropic rearrangement, with the reaction shown on the left. In this experiment molecular modelling will be used to predict the preferred reaction mechanism for this sigmatropic rearrangement.
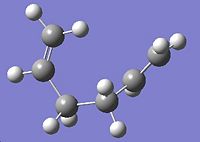


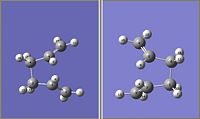
Initially 1,5-hexadiene was drawn on Gaussview, with the 4 central carbon atoms in an anti-peri planar configuration, and the structure was optimised using the Hartree Fock method using the 3-21G basis set. The optimised energy of the structure was then found to be -231.69260 Hartree (0.04 kcal/mol) and the point group was found to be C2. This conformation was found to be the gauche 6 conformation in Appendix 1 The conformation of 1,5-hexadiene with the central 4 atoms in the gauche formation was then optimised using the same method and basis set, the energy was found to be -231.689160 Hartree (2.2kcal/mol) and the point group was found to be C1. This conformation was found to be anti1 in appendix 1. Within these two examples the anti-peri planar structure was found to be the lowest in energy (when the energies are converted to kcal/mol). A lower energy conformation was found with an energy of -231.69266 Hartree (0.00kcal/mol). This conformation was found to be gauche3 in appendix 1 and is the lowest possible energy conformation. This is unusual as at a glance it would be expected that the gauche conformer's terminal carbons would undergo steric repulsions due to their close proximity, which would result in a higher energy conformation than the anti. The anti2 conformation was found to have Ci geometry and an energy of -231.69254 Hartree.
The anti2 conformation was then re-optimised using the DFT method and the 6-31G(d) basis set. The energy was found to be -231.69254 Hartree by this method. The overall geometry did not change, and the point group remained Ci. A frequency calculation at the same level was then carried out. From the frequency calculation it was found that there were no negative frequencies, therefore the molecule has optimised correctly. The thermochemical data for the molecule was calculated at both 0K and 298.15K.
| Energies | 0K/Hartree | 298.15K/Hartree |
| Sum of electronic and zero point energies (Known as Zero Point energy) | -234.468312 | -234.469212 |
| Sum of electronic and thermal energies (These values take into account the vibrational,rotataional and translational energies at the specified temperatures | -234.468312 | -234.461856 |
| Sum of electronic and thermal Enthalpies (These values take into account a correction for RT (H = E + RT)) | -234.468312 | -234.460912 |
| Sum of electronic and thermal Free Energies(Includes the entropic contribution G = H - TS) | -234.468312 | -234.500821 |
All calculations were run at a pressure of 1 atmosphere.
It is difficult to determine which computational method is more accurate as both are medium level calculations with a reasonable degree of accuracy. If more accuracy was required a higher level method could be employed, but the computational time and therefore costs associated with the calculation would be much higher.
Optimising the chair and boat transition structures of the Cope rearrangement
Chair Conformer
So the chair and boat transition structures could be optimised, it was necessary to draw them.
To draw the chair transition state a CH2CHCH2, allyl, fragment, was drawn then optimised using the Hartree-Fock method and 3-21G basis set, then copying the fragment and creating two fragments which look like the transition state.
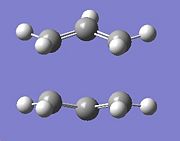 |
 |
An optimisation+frequency calculation was done on the transition state. Optimising a transition state is harder than an optimisation on a molecule, as for the calculation to run correctly it is necessary to know the location of the reaction coordinate. To attempt to get around this the force matrix constant of the transition state will be calculated and updated during the calculation.
Once the calculation had completed the frequencies of the vibrations were looked at and there was found to be a vibration at an imaginary frequency of 840cm-1.
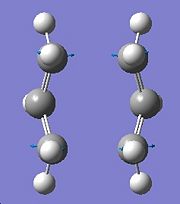
The transition state was then re-optimised this time using the frozen coordinate method, during this the bond forming/breaking distances were set to be equal to 2.2Å. Then the bond forming/breaking distances were optimised using a normal guess Hessian which has been modified so that it has the necessary information about the bond coordinates the differentiation is happening along. Once this had been done the structure of the transition state was found to look like the structure that was optimised earlier, see picture on left. The bond forming/breaking distances were found to be 2.1393Å.
Boat Structure
For the boat transition structure it was optimised using the QST2 method, the 1,5-hexadiene optimised previously was used to create the reactant and product molecule in separate geometries. These molecules were then numbered according to where the bonds in the reactant will be, after the reaction, in the product. Without modification of the structure of the molecules the opt+freq calculation fails. Once the central dihedral angle (corresponding to the central 4 carbon atoms) is changed to 0° and the two angles within the central 4 carbon atoms are changed to 100° in both molecules, the calculation then runs. This is because if the QST2 method deals with the more linear structures then it cannot get to the boat transition structure. If the molecules are modified to look more like the transition state then the QST2 method can perform the calculations on them. Once the boat transition state had been optimised it was found that there was one imaginary vibration at 841cm-1.
From the boat and chair conformers it is not possible to see which conformer of 1,5-hexadiene has lead to which transition state. It is possible to use a method which makes it possible to use a transition sturcture and from that follow the minimum energy path to reach the lowest energy conformation. This method is the Intrinsic Reaction Coordinate method. Using this method it was attempted to find the lowest energy geometry for the chair transition structure. The IRC calculation was run on the previously optimised chair transition structure from the frozen coordinate method, using the Hartree-Fock method and the 3-21G basis set. The reaction coordinates were only computed in the forward direction as the chair transition structure is symmetrical, and the number of points along the IRC computed was set to 50.
The results of this calculation were that the calculation did not have enough points along the IRC to calculate the minimum geometry. To try and reach the minimum geometry the number of points along the IRC was increased to 70. There was found to be little difference in the conformation produced by 70 points so a calculation was performed using 150 points. The results of this calculation showed, in the intermediate geometries, a bond being formed between the two segments of the transition state.
Activation Energies
The chair and boat transition states were both reoptimised, this time using the DFT B3LYP method and 6-31Gd basis set. Frequency calculations were then performed using the same method and basis set. The gauche conformer of 1,5-hexadiene, which was found to be the lowest energy conformer, was also reoptimised at the same level and a frequency calculation performed on it. The optimised energy of the gauche 1,5-hexadiene was found to be -234.62342934 Hartree.
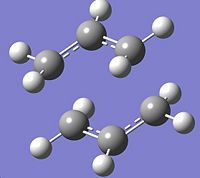 |
 |
| Conformer | Energy/Hartree | Energy of gauche-Energy of molecule/Hartree | Activation Energy/kcalmol-1 | Experimental Value/kcalmol-1 |
| Chair | -234.6740355 | 0.0506062 | 34.91679319 | 33.5±0.5 |
| Boat | -234.62342934 | 0.06085213 | 41.98618427 | 44.7±2.0 |
The DFT B3LYP method with the 6-31Gd basis set provides a good approximation of the activation energies of the reaction, this suggests that it is a good level of method for calculations of this nature.
The Diels Alder Cycloaddition
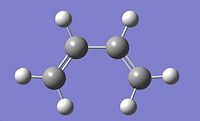
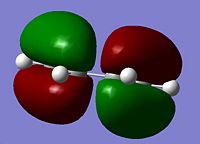
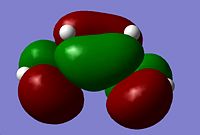
The Diels Alder cycloaddition is a nobel prize winning reaction1 involving a reaction between a diene and a dienophile, in the shape of a substituted alkene. Both of the reactants can take many forms but the diene must be in the cis-conformation. A typical diene for the reaction is cis-butadiene, the molecule was drawn on Gaussview and optimised using the AM1 semi-empirical method. Once optimised an energy calculation was run using the same method to calculate the molecular orbitals of the cis-butadiene. The Diels-Alder reaction takes place between the HOMO and LUMO of the reactants and therefore it was these molecular orbitals which were focused on.
 |
 |
 |
 |
The HOMO is anti-symmetric with respect to the plane of symmetry of cis-butadiene. The LUMO is symmetric with respect to this plane.
Transition state geometry and investigation into reaction pathway
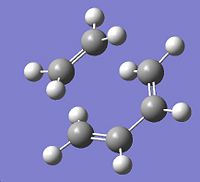
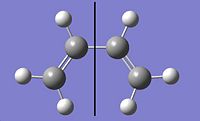
An approximation of the transition state between cis-butadiene and ethylene was drawn on Gaussview by drawing bicyclo[2.2.1]heptane and atoms removed until it resembled the predicted transition state. The frozen coordinate method was used to optimise the transition state. Initially the bond forming/breaking distances were frozen to 2.2Å and the rest of the molecules optimised to a minimum using the AM1 semi-empirical method. The chk file of the calculation was then used to perform a derivative along the bond forming/breaking distances, using a normal Hessian. An optimisation and frequency calculation was then performed on the transition state. The resulting transition state is shown below.
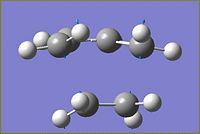
Typical sp3 C-C bond lengths are 1.54Å and sp2 C-C bond lengths are 1.47Å.3 The C-C bond lengths in the transition state are 1.38Å (sp2 C-C) and 1.40Å(sp3 C-C). The transition state bond lengths are shorter than literature values. This could be due to inadequacies in the calculation used, or could suggest that the system has aromatic characteristics, as a delocalised π system results in shortening of C-C bond lengths. The resulting length of the bond forming/breaking distances, after optimisation, was found to be 2.12Å. The Van der Waals radius of a carbon atom is 170pm4 when taking this into account it is possible to see that although the terminal carbons are not within, sp2 or sp3, carbon bond length distances of each other, they are close enough to each for some form of bonding interaction to take place between them.
The vibration corresponding to the bond formation/breaking is imaginary and occurs at 959cm-1. The formation is synchronous with both of the bonds forming between ethylene and cis-butadiene occuring at the same time. The lowest positive frequency occurs at 147cm-1 and corresponds to a 'twisting' motion between the two molecules. This is an asynchronous motion and does not resemble the transition state.
 |
 |
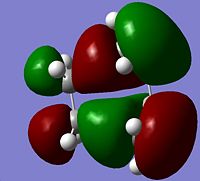
The HOMO of the transition state is clearly anti-symmetric and the LUMO clearly symmetric.
The HOMO is made up of the molecular orbitals from the butadiene and ethylene, the mixing of the orbitals implies that bonding is occuring between the two molecules. The two orbitals used to form the HOMO are the HOMOs of both ethylene and butadiene, both of which are anti-symmetric. For the reaction to proceed there must be a promotion of electrons into the transition state HOMO from the ethylene and butadiene HOMOs. In the singlet ground state only anti-symmetric promotions are allowed, as all the HOMOs are anti-symmetric promotion between them is allowed, therefore the reaction taking place in the transition state is allowed.
Regioselectivity of the Diels-Alder reaction
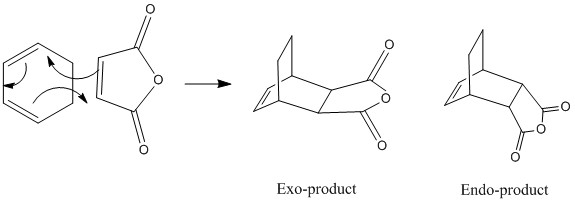
When cyclohexa-1,3-diene undergoes a Diels-Alder reaction with maleic anhydride the endo product is the major product. This reaction has two potential transition states the endo and exo, to investigate why the endo product is the major product both of these transition states will be modelled and from this the reaction they undergo investiagted.
Before the transition states could be modelled, cyclohexa-1,3-diene and maleic anhydride had to be drawn in Gaussview and individually optimised to minimise the potential errors and calculation time for the optimisation of the transition states. Both were optimised to using the HF method and the 3-21G basis set. Once this had been done, both of the optimised molecules were used to create the two transition states.

The transition states were then themselves optimised using the frozen coordinate method. The distances between which the bonds from between the two molecules were frozen to 2.2Å and the molecules then had an opt+freq calculation to a transition state done on them, using the HF method and the 3-21G basis set. Once this had been done, the distances which had previously had their coordinates frozen were unfrozen and a normal guess Hessian was used to differentiate along the bond. An optimisation was then done on the two transition states again, at the HF 3-21G level. Pictures of both of the optimised transition states are shown below.

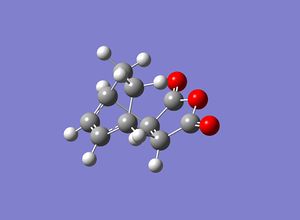
The relative energies of the transition states were determined, the exo transition state was found to have a relative energy of -605.65217922Hartree and the endo transition state -605.72132080Hartree. The endo transition state is the most stable as it is the lowest energy conformation. These results correspond with the view that the reaction is kinetically contolled and therefore the exo state should be higher in energy.
In both transition states the bond lengths of some C-C distances were measured:
| C-C bond forming distances/Å | C=C bond length in maleic anhydride/Å | C=C bond length in cyclohexa-1,3-diene/Å | C-C bond length in cyclohexa-1,3-diene/Å | |
| Endo transition state | 2.23 | 1.53 | 1.51 | 1.56 |
| Exo transition state | 2.26 | 1.54 | 1.52 | 1.56 |
In both of the transition states the carbons between which the bonds will form are within the distances set by the VdW radius of C which determines whether interaction will occur. The endo transition state has a slightly larger interaction that the exo transition state, as in the exo transition state there is a slight repulsive force due to interaction between the hydrogens on the cyclohexa-1,3-diene which are on the sp3 hybridised carbon atoms. In the endo transition state due to the opposite orientation of the maleic anhydride this interaction does not occur and therefore there will be no repulsive forces caused by this. According to the literature this combined with a steric clashing of the oxygen atoms on the maleic anhydride and the hydrogens on the cyclohexa-1,3-diene is what causes the exo transition state to be slightly higher in energy and therefore the minor product in the reaction.
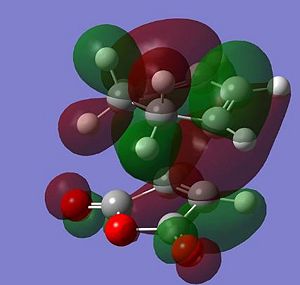

According to the following journal DOI 'secondary orbital overlap' plays a part in the predominance of the endo product over the exo product. 'Secondary orbital overlap' is based on molecular orbital theory and suggests that the endo transition state is stabilised by interaction between atomic orbitals which do not influence the formation/breaking of bonds specifically those on the oxygen atoms and the diene. In the exo transition state the positioning of the oxygen atoms away from the diene means that this secondary orbital overalp cannot occur, perhaps suggesting why the exo product is the predominant product. This theory relies on the concept of localised areas of electron density which manifest themselves in the forms of orbitals, in this case specifically between the interaction of the atomic orbitals on the terminal ends of the diene and the orbitals on the ends of the alkene bond in the maleic anhydride.
The HOMOs for both transition states were modelled using the same HF 3-21G level as before, both HOMOs are anti-symmetric. The orbitals on the maleic anhydride and cyclohexa-1,3-diene have a strong overlap in the bond forming regions between the two, suggesting a correct transition state has been identified. According to the journal the secondary orbital overlap is stronger in the endo transition state, this is visible in the diagrams shown as there is more electron density shown on the central oxygen atom of the maleic anhydride in the endo transition state.
References
1. Diels, O.; Alder, K. (1928). "Synthesen in der hydroaromatischen Reihe". Justus Liebig's Annalen der Chemie 460: 98. DOI
2. Handbook of Chemistry & Physics, 65th Edition, CRC Press, ISBN 0-8493-0465-2
3. Fox, MA and JK Whitesell. Organic Chemistry. 1st edition, 1994. pp1083
4. Bondi, A. "Van der Waals Volumes and Radii". J. Phys. Chem, 1964, 68 (3) pp441–51. DOI