Rep:PS4615 Transition States and Reactivity

Introduction

In this experiment, the reactivity of different Diels-Alder reactions were explored computationally by carrying out energy calculations of the reactants, products and more importantly the transition states. The two computational methods used are the PM6 (semi-empirical) and B3LYP (Density Functional Theory).

Potential Energy Surface (PES) and Transition States

A potential energy surface (PES) describes the potential energy of a system, especially a collection of atoms or molecules, in terms of certain parameters. In this case, the PES describes the potential energy of the system when it is in different geometries. Its dimensionality depends on the number of atoms in the system. Using 3-dimensional cartesian coordinates to describe the position of the atoms in the system, it can be deduced that the dimensionality would be $3N$. Although, the potential energy, hence the PES does not depend on the absolute position of the atoms, but only their relative positions. As a result, the translational and rotational degrees of freedom (3 each) can be removed from the dimensionality of the PES. As a result, the dimensionality of the PES becomes:

$3N-6$ (1)

where N is the number of atoms in the system.

The most interesting points on PES's are stationary points. A stationary point on a PES is a point with nuclear configuration where all the forces vanish. In other words, it is where every component of the gradient in all directions/dimensions $\alpha$ is zero.

$\frac{\delta V(X)}{\delta X_{\alpha }}=0$ (2)

where $V(X)$ represents the potential energy of a particular coordinate $X$. $\alpha$ represents a particular dimension in the PES where $\alpha ϵ[3N-6]$. The following summarises the three points:

1. Minima: corresponds to stable (global minimum) species or quasi-stable (local minima) species. Examples include the reactants, intermediates and products.

2. Transition states: saddle points which are minimum in all dimensions in the PES except for one, where it is a maximum in that dimension. In other words, the transition state is the true kinetic barrier of a reaction.

3. Higher-order saddle points: a minimum in all dimensions except for $n$ number of dimensions, where $n>1$. It is the maximum points in the $n$ dimensions.

At the stationary point, since the first derivative of the potential energy (which is the force) is zero, the leading terms of a Taylor expansion of the potential energy $V(Q)$ at a stationary point $M$, where $Q=X-M$ are quadratic.

$V(Q)=\frac{1}{2}\sum _{\alpha =1}^{3N-6}{\omega }_{\alpha }^2{Q}_{\alpha }^2+K$ (3)

where $Q_{\alpha }$ represents the $\alpha$ component of $Q$, ${\omega }_{\alpha }$ represents the Hessian eigenvalues of $\alpha$ of $Q$ and $K$ represents the higher order terms in the Taylor expansion (Harmonic Approximation).

The Hessian eigenvalues determine the characteristic of the stationary points. More importantly, the Hessian index, which is the number of negative Hessian eigenvalues, determines whether the stationary point is a minimum, transition state or high order saddle point. It also corresponds to the number of imaginary (negative) vibrational frequencies. For minimum points, the Hessian index is zero. This means all the vibrational frequencies must be positive. On the other hand, a transition state is a stationary point with a Hessian index of 1. This means that the frequency analysis of the transition state must result in one imaginary/negative vibrational frequency. A saddle point has a Hessian index of more than 1, which again can be observed from the output frequencies after running a vibrational analysis. h Nf710 (talk) 22:52, 28 March 2018 (BST) You have clearly read beyond the script used your notes from Molecular reaction dynamics. Well done. You havent meantioneed the normal modes which the Hessian eigenvalues are paired too. They are linear compinations of the degrees of freedom wbich when you move back and forth along these vectors are vibrations that you see.

Figure 1. The transition state (TS) indicated on a sample PES. MEP stands for the minimum energy path, which in this case is the IRC.

In this experiment, the energies of the reactants, transition states and the products of different pericyclic reactions were computed. The difference between the energy of the reactions' transition state and reactants were used to quantify the kinetic barriers of the reactions. In addition, the minimum energy paths that connect the reactants, transition states and products were visualised to show the reaction coordinate of the reactions (IRC).

Methods

Gaussian was used for the computations in this experiment, where GaussView was used as a user interface and visualisation of the molecular orbitals. There are three methods that can be used to compute the transition state geometries and energies of the pericyclic reactions in this experiment. The following outlines the methods available:

Method 1. This method only work for small systems, where a guessed transition state is optimised in one single step with the PM6 method. This only work for simple systems because for complex systems with many atoms, the PES will be very complex with multiple higher order saddle points around the true transition state. It is the fastest method but at the same time the least reliable as the converged structure might actually be a higher order saddle point due to the complex PES.

Method 2. Again, this method requires guessing the transition state structure. Although, the atoms that is involved in the reaction are frozen, with the resulting structure optimised to a minimum before the whole guessed transition state is optimised to find the converged structure. This ensures that the guessed structure is as close to the transition state as possible in the PES, providing the fastest reliable method for computing the geometry of transition states.

Method 3. Compared to the other 2, this method does not require the guessing of the transition state. It is the most reliable method of the three, but take the longest time due to additional steps required. The product or the reactants of the reaction is optimised individually to a minima. This is followed by altering the bond lengths so that the structure resembles the transition state. The atoms involved in the reactions are then frozen like Method 2, optimised to a minimum before being optimised again to get the converged structure.

From earlier, it was mentioned how the PES can be used to determine the geometries and energies of transition states, but not how they can be generated. For very simple systems, the PES can be fitted to experimental data. For more complex and reactive systems, the PES must be generated by quantum mechanical calculations (eg. semi-empirical, DFT, etc).

The Parameterisation Method 6 (PM6) method, which is a semi-emipirical method, is an approximate version of the Hartree-Fock method. Many approximations are made to calculate the Hamiltonian of the Schrodinger equation of the system. Namely, some two-electron and sometimes one-electron integrals are neglected to speed up the computation and reduce the computation cost. To make up for this, empirical parameters are used to make up for these approximations. For the remaining integrals, some are computed exactly, but some are computed using parameters obtained from experiments (hence semi-empirical). This means that the method will work well for systems that experimental parameters are available, but not reliable otherwise.

The B3LYP method used in this experiment is a hybrid method that contains elements from Density Functional Theory (DFT) and Hartree-Fock theory. The 'B3' part specifies the exchange functional (Hartree-Fock) used to run the computation, whereas the 'LYP' specifies the correlation functional (DFT). In other words, it utilises the Hartree-Fock theory to calculate the exchange integral terms in the Hamiltonian. In addition to that, it uses DFT to approximate the correlated motions of electrons in the system. 6-31G basis set was used to model the electronic wavefunctions. Overall, B3LYP carry out calculations more accurately compared to PM6, but takes longer time and computation cost.

Nf710 (talk) 23:26, 28 March 2018 (BST) This section was written extremely well. You could have gone into more detail into the basis sets used and added some more equations to example the quantum chemstry theories. But you have clearly read beyond the script and shown further understanding. Well done.

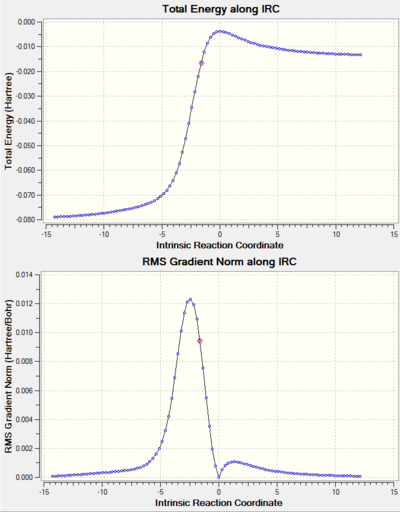
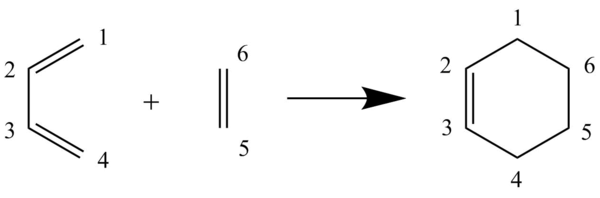
Exercise 1: Reaction of Butadiene with Ethylene

(Fv611 (talk) Very well done across the whole exercise. Good job!)

Figure 2. The reaction scheme between butadiene and ethylene to make cyclohexene.

Corresponding Log files

PS4615_1_ETHENE_MIN_OPT_FREQ_PM6.LOG

PS4615_1_BUTADIENE_MIN_OPT_FREQ_PM6_AGAIN_BREAK_SYM.LOG

PS4615_1_CYCLOHEXENE_MIN_PM6.LOG

PS4615_1_TS_BERNY_PM6_2.LOG

PS4615_1_TS_IRC_PM6.LOG

Transition State MO diagram

Figure 3. The transition state MO diagram of the reaction. Note that the energies of the MOs are obtained (in Hartrees) from Gaussian.

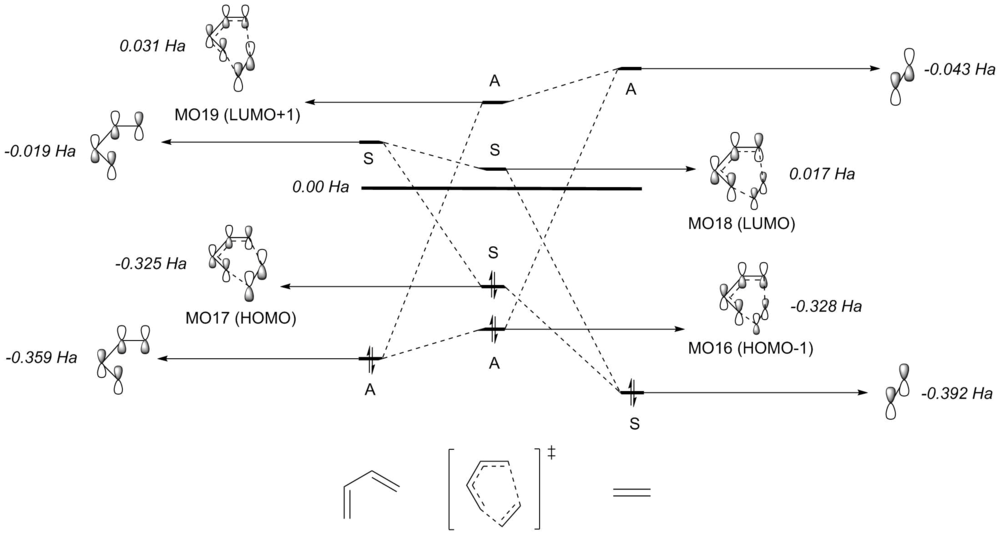
The MO diagram as shown in figure 3 was constructed using the MOs from the reactants optimised using Gaussian. In addition, the MOs of the transition state were obtained using Method 3, where they were used to correlate the reactants' MOs that interacted to make up the TS MOs. The MOs obtained from the calculation are shown below in table 1. The symmetry of the MOs were determined by following the steps as described below:

1. Identify a plane of symmetry in the MOs.

2. If the phase of the atomic orbitals on both sides of the plane are the same, then the MO is symmetric (S). If it is in the opposite phase, then it must be antisymmetric (A).

Table 1. The HOMO and LUMO of butadiene, ethylene and the transition state of the reaction.

Butadiene HOMO	Butadiene LUMO	Ethylene HOMO	Ethylene LUMO
Transition State HOMO-1	Transition State HOMO	Transition State LUMO	Transition State LUMO + 1

Firstly, the HOMO and LUMO of the transition structure was analysed. It can be seen from the MOs that it is a result of the interaction between the HOMO of the reactant ethylene and LUMO of butadiene, both of which are symmetric. As a result, the transition state MOs must be symmetric. This was further confirmed by carrying the symmetry analysis described on the TS MOs. As for the HOMO-1 and LUMO+1 of the TS, it was determined that they are the result of the interaction between the LUMO of ethylene and HOMO of the butadiene. The reactants' MOs are all antisymmetric, which resulted in antisymmetric HOMO-1 and LUMO+1 of the TS.

From this, it can be concluded that only orbitals with the same symmetry can interact to produce molecular orbitals. Furthermore, it is possible to draw up the conclusion that in order to determine whether the reaction is forbidden or allowed, the MOs of the reactants must be analysed. For an allowed reaction, the orbitals of the reactants must have the same symmetry. On the other hand, if the orbitals of the reactants does not have the same symmetry, the reaction is then said to be forbidden. This can be explained further by considering the overlap integrals $S_{AB}$ of the orbitals. It is a quantitative way of analysing the extent of interaction between the orbitals. For symmetric-symmetric or antisymmetric-antisymmetric orbital interaction, the overall overlap integral is non-zero, leading to two new MOs (the TS MOs in this case). As for antisymmetric-symmetric orbital interaction, the overlap integral is zero leading to no MOs formed.

Carbon-Carbon Bond Length Analysis

Table 2. The Carbon-Carbon bond lengths for the reaction obtained from the calculation.

	Bond Length (Å)
C-C Bond	Butadiene (Reactant)	Ethylene (Reactant)	Transition State	Cyclohexene (Product)
C1-C2	1.333	N/A	1.380	1.491
C2-C3	1.471	N/A	1.411	1.363
C3-C4	1.333	N/A	1.380	1.491
C4-C5	N/A	N/A	2.116	1.583
C5-C6	N/A	1.327	1.382	1.560
C6-C1	N/A	N/A	2.113	1.583

During the course of the reaction, the different C-C bonds change as it progresses from the reactant to the transition state and finally the product. Firstly, the hybridisation of the carbons in the reactants and products must be discussed to make the explanation easier. It is clear from the reaction scheme that all of the carbons in the reactants are $s{p}^2$ hybridised. After the reaction has proceeded to the product, the hybridisation of C2 and C3 stays the same, whereas the rest of the carbons changed their hybridisation to $s{p}^3$.

The analysis of the hybridisation of the carbons are essentially for identifying the change in the bond lengths. From Table 2, it can seen that C1-C2/ C3-C4 bond lengths (they are the same due to symmetry) changes from 1.333 Å (double bond) to 1.491 Å ($s{p}^2-s{p}^3$ single bond), with the bond length of 1.380 Å for the transition state. One of the reasons why the bond length increases is because the bond length changes from being a double bond to being a single bond. Moreover, the hybridisation of the carbons that make up the bonds changes from being $s{p}^2-s{p}^2$ to $s{p}^2-s{p}^3$. Having less s-character in the hybridisation increases the bond length, as s-orbital electron densities are closer to the nucleus.

As for C5-C6, the bond changes from 1.327 Å (double bond) to 1.560 Å ($s{p}^3-s{p}^3$ single bond), with the bond length of 1.382 Å for the transition state. Again, the same analysis can be made for the discussion of the changes in the C-C bond lengths. Although, it is worth noting that the C5-C6 bond length is greater than the C1-C2 / C3-C4 bond lengths in product. One possible explanation is that even though both of the bonds has a bond order of 1, the hybridisation of C5-C6 bond is $s{p}^3-s{p}^3$. Hence, there is less s-character in the bond, making it longer. For C2-C3, the bond length changes from 1.471 Å ($s{p}^2-s{p}^2$ single bond) to 1.362 Å (double bond) with the bond length of 1.411 Å for the transition state. For this case, the transition state bond length is observed to be shorter than the reactants compare to the other cases discussed. This is because for this case, instead of the double bonds in the reactant partially breaking (decreasing in electron density) in the transition state, a double bond is partially forming (increasing electron density) here, making the bond length decrease.

As for the new bonds created (C1-C6 and C4-C5), the corresponding bond lengths for both of them is 1.583 Å ($s{p}^3-s{p}^3$ single bond). As for the transition states, the corresponding partially formed bond lengths are 2.113 Å and 2.116 Å for C1-C6 and C4-C5 respectively. This is shorter than Van der Waals radii between two carbons of 3.4 Å (each being 1.7 Å) but at the same time longer than a typical C-C single bond. This indicates that the orbitals in the carbons involved are drawn together, interacting, and about to form new bonds in the transition state.

From this, it can be approximated that the typical bond length for C-C double bonds is 1.3 Å (lit. 1.34 Å), 1.6 Å (lit. 1.54 Å) for $s{p}^3-s{p}^3$ single bonds, and 1.5 Å for $s{p}^2-s{p}^3$/$s{p}^2-s{p}^2$ single bonds, with $s{p}^2-s{p}^2$ single bonds slightly shorter than $s{p}^2-s{p}^3$ single bonds (lit. 1.50 Å for $s{p}^2-s{p}^3$ and 1.47 Å for $s{p}^2-s{p}^2$) .

Transition State Vibrations

Figure 4. The IRC of the reaction.

Figure 5 shows the vibration of the transition state.

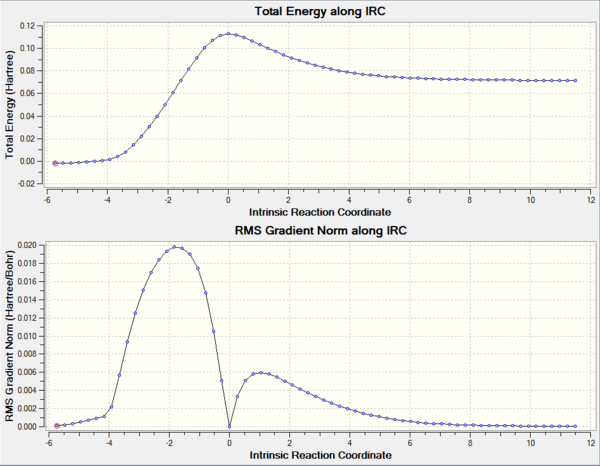
By running an IRC calculation, the vibration calculation was confirmed to be successful (see Figure 4). In addition, vibration corresponding to the transition state is illustrated (Figure 5). As described in the introduction, the frequency of this particular vibration of the transition state is negative. From the IRC of the reaction, it can be deduced that the bond formation between terminal carbons in butadiene and ethylene is synchronous, as the bond formation occurred at the same time. Also, it can be seen from the Jmol that the carbons involved in forming the new bonds approach each other at the same time and synchronously. This results in synchronous bond formation.

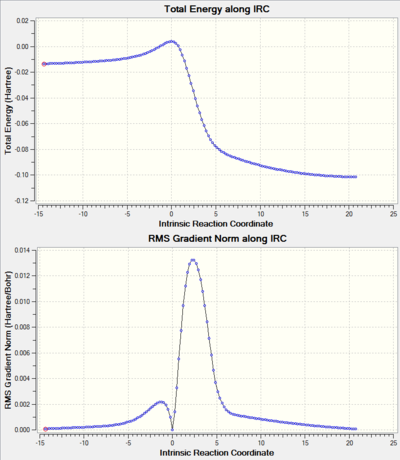
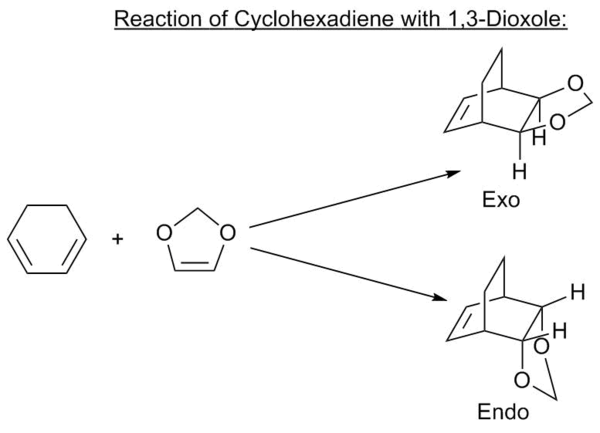
Exercise 2 - Reaction of Cyclohexadiene and 1,3-Dioxole

Figure 6. The reaction scheme of the reaction. Note that there are two possible products from the reaction.

Corresponding Log files

Reactants:

PS4615_2_CYCLOHEXADIENE_MIN_PM6.LOG

PS4615_2_CYCLOHEXADIENE_MIN_B3LYP.LOG

PS4615_2_1_3_DIOXOLE_MIN_PM6.LOG

PS4615_2_1_3_DIOXOLE_MIN_B3LYP.LOG

ENDO TS and products:

PS4615_2_TS_BERNY_ENDO_PM6.LOG

PS4615_2_TS_BERNY_ENDO_B3LYP.LOG

PS4615_2_PRODUCT_ENDO_MIN_PM6.LOG

PS4615_2_PRODUCT_ENDO_MIN_B3LYP.LOG

PS4615_2_TS_IRC_ENDO_PM6.LOG

EXO TS and products:

PS4615_2_TS_BERNY_EXO_PM6.LOG

PS4615_2_TS_BERNY_EXO_B3LYP.LOG

PS4615_2_PRODUCT_EXO_MIN_PM6.LOG

PS4615_2_PRODUCT_EXO_MIN_B3LYP.LOG

PS4615_2_TS_EXO_IRC_PM6.LOG

Transition State MO Diagram and Analysis

(Fv611 (talk) Nice MO diagrams. Could have extended the discussion a little bit.)

Figure 7. The transition state MO diagram of the reaction (ENDO). Note that the energies of the MOs are obtained (in Hartree) from Gaussian.

Figure 8. The transition state MO diagram of the reaction (EXO). Note that the energies of the MOs are obtained (in Hartree) from Gaussian.

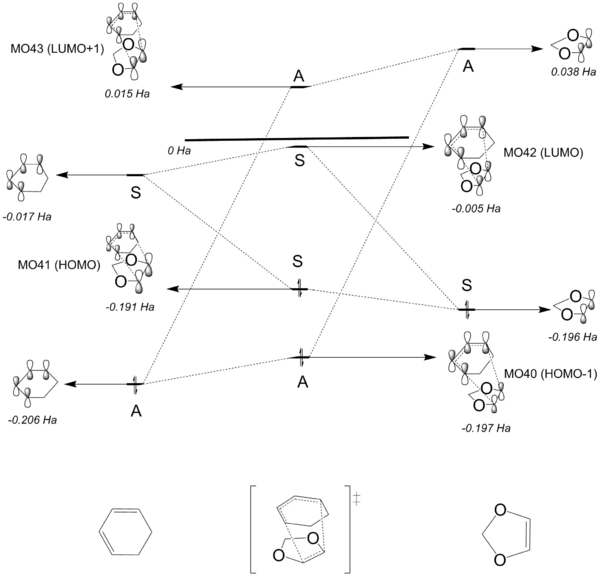
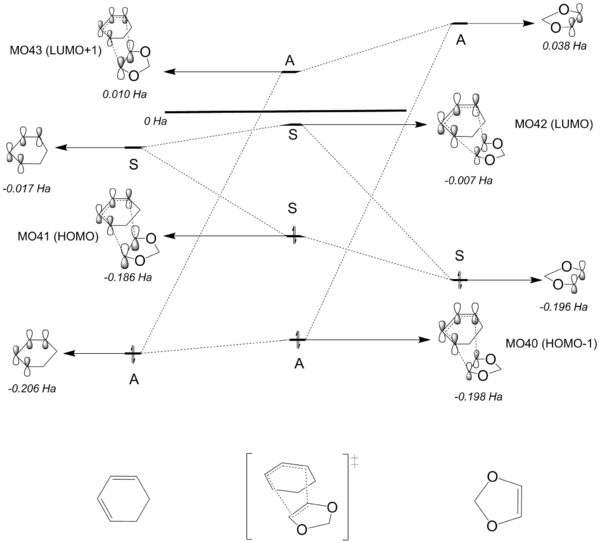
Figure 7 illustrates the molecular orbital diagram of the transition states for the Diels-Alder reaction. The MO diagrams were constructed by carrying out the same analysis on the relevant MOs of the reaction's transition states (see table 3 for the MOs of the transition states). Again, it was observed that MOs that has the same symmetry interact to form the TS MOs. It can be seen that for each case, the overall energy of the transition state for the ENDO case is lower compared to the transition state for the EXO product. Qualitatively speaking, this indicates that the kinetic barrier/activation energy for the EXO case is higher, resulting in the pathway being kinetically stable compared to the ENDO pathway. A more quantitative analysis is discussed in the Thermochemistry section below.

Table 3. The relevant molecular orbitals of the transition states of the Diels-Alder reaction.

TS ENDO HOMO-1	TS ENDO HOMO	TS ENDO LUMO	TS ENDO LUMO+1
TS ENDO HOMO-1	TS ENDO HOMO	TS ENDO LUMO	TS ENDO LUMO+1

Diels-Alder reactions such as this case can be classified as either normal or inverse electron-demand. For a qualitative analysis, it can be said that for a normal electron-demand Diels-Alder reaction, the diene is electron rich whereas the dienophile is electron deficient. On the other hand, the diene is required to be electron deficient, where the dienophile is electron rich for an inverse electron-demand Diels-Alder reaction. For a more quantitative analysis, whether the reaction is normal or inverse electron-demand depends on the relative energies of the HOMO and LUMO of the reactants involved in the reaction. For a normal electron-demand reaction, the HOMO and LUMO of the dienophile is lower in energy compared to the respective HOMO and LUMO of the diene. As a result, there is a strong interaction between the HOMO of the diene and the LUMO of the dienenophile as they have similar energies, forming the HOMO and LUMO of the product. An example of this is the Diels-Alder reaction in Exercise 1 (see figure 3 for the MO diagram). For an inverse electron-demand reaction, the HOMO and LUMO of the dienophile is higher in energy compared to the respective HOMO and LUMO of the diene. For this case, the HOMO of the dienophile and LUMO of the diene interact strongly to produce the HOMO and LUMO of the product. For the Diels-Alder reaction between cyclohexadiene and 1,3-dioxole, the reaction is an inverse electron-demand reaction, with explanations as described above. One of the reasons why the HOMO and LUMO of the dienophile has such high energies, surpassing the MOs of the diene, is because of the electron donating effect of the two oxygens next to the alkene, raising the energy of MOs of the dienophile. Figure 9 illustrates the inverse electron-demand characteristic of the (ENDO) reaction nicely, with the energies of the product MOs calculated by running an optimisation on the product structure (B3LYP).

Figure 9. A simplified MO diagram (ENDO product) illustrating the inverse electron demand nature of the reaction.

Nf710 (talk) 23:38, 28 March 2018 (BST) This was a very good analysis, but were the reactant MOs energies calculated from a single point energy with both on the same surface. or seperatly? Because then you cannot compare the energies if they are seperate as the hamiltonians have different potentials as they have different numbers of atoms/electrons

Thermochemistry

Table 4 The table shows activation energies and the Gibbs free energies of the ENDO and EXO Diels-Alder reaction.

	Activation Energy / $kJmo{l}^{-1}$	Gibbs Free Energy / $kJmo{l}^{-1}$
ENDO	+159.8	-67.4
EXO	+167.7	-63.8

From table 4, it can be seen that the ENDO pathway has a lower activation energy compared to the EXO pathway, making it kinetically favourable. This is because the HOMO of the ENDO transition state is further stabilised by secondary orbital interactions. From table 5, it can be seen that the p orbitals on the oxygens of the dienophile interacts with the delocalised π orbitals on the diene, which has a stabilising effect on the transition state. Secondary orbital interaction is absent in the EXO pathway, as transition state does not have the correct geometry for it. This makes the energy of the ENDO transition state lower than that of the EXO pathway, making it kinetically favoured.

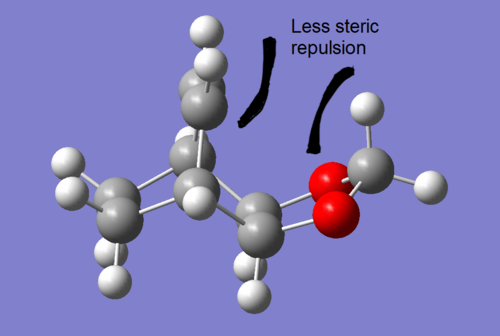
In addition, the ENDO pathway is more exothermic compared to the EXO pathway, making it the thermodynamically favoured compared to the other pathway. As a result, this makes the ENDO product thermodynamically more stable than the EXO product. Secondary orbital interactions within the ENDO product is one of the factors that make the energy of the ENDO product lower than the EXO product. This is the same interaction as described above, with the EXO product lacking in the stabilising interaction due to its geometry. Furthermore, unfavourable steric interactions between the dioxole group and the ethylene bridgehead in the EXO product may have played a significant role in increasing its energy, making it less exothermic. This effect is likely to be less significant for the ENDO product, as the dioxole is closest to the saturated bridgehead, resulting in less interaction with the hydrogen atoms (see table 6 for illustration).

Table 5 The table shows the HOMO of the transition states with the isovalue set to 0.01 to show secondary orbital interactions.

TS ENDO HOMO	TS EXO HOMO

Table 6 The table shows the steric interactions in the ENDO and EXO product.

ENDO product	EXO product
|	|

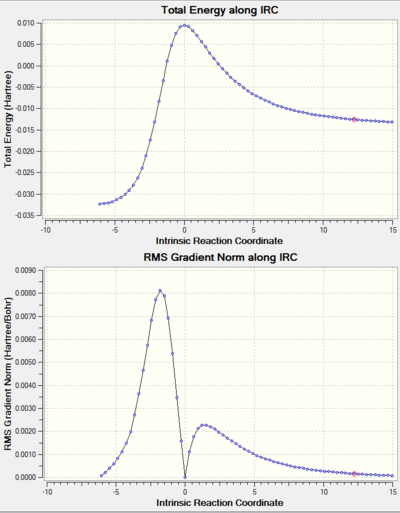
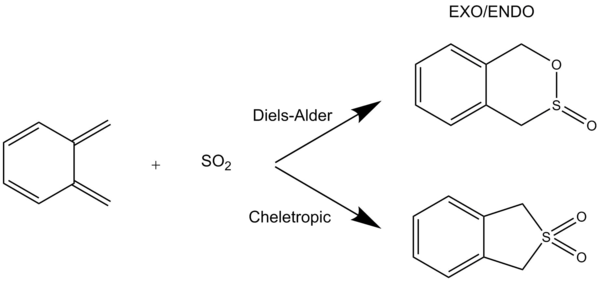
Exercise 3: Diels-Alder vs Cheletropic

Figure 10. The reaction scheme of the reaction. Note that there are two possible reaction pathways, including Diels-ALder and Cheletropic.

Corresponding Log files

Reactants:

PS4615_3_REACTANT_DIENE_MIN_PM6.LOG

PS4615_3_REACTANT_SO2_MIN_PM6.LOG

Diels-Alder ENDO TS and products:

PS4615_3_DA_TS_BERNY_ENDO_PM6.LOG

PS4615_3_DA_TS_IRC_ENDO_PM6.LOG

PS4615_3_DA_PRODUCT_MIN_ENDO_PM6.LOG

Diels-Alder EXO TS and products:

PS4615_3_DA_EXO_TS_BERNY_PM6.LOG

PS4615_3_DA_EXO_TS_IRC_PM6.LOG

PS4615_3_DA_EXO_PRODUCT_MIN_PM6.LOG

Cheletropic TS and products:

PS4615_3_CHELETROPIC_TS_BERNY_PM6.LOG

PS4615_3_CHELETROPIC_TS_IRC_PM6.LOG

PS4615_3_CHELETROPIC_PRODUCT_MIN_PM6.LOG

Alternative Diels-Alder ENDO TS and products:

PS4615_3_ALT_DA_ENDO_TS_BERNY_PM6.LOG

PS4615_3_ALT_DA_ENDO_TS_IRC_PM6.LOG

PS4615_3_ALT_DA_ENDO_PRODUCT_MIN_PM6.LOG

Alternative Diels-Alder EXO TS and products:

PS4615_3_ALT_DA_EXO_TS_BERNY_PM6.LOG

PS4615_3_ALT_DA_EXO_TS_IRC_PM6.LOG

PS4615_3_ALT_DA_EXO_PRODUCT_MIN_PM6.LOG

IRC

Table 7 The table shows the different IRC of the Diels-Alder and Cheletropic reaction. Note that the IRC of the Diels-Alder EXO IRC is in the opposite direction.

Diels-Alder ENDO IRC	Diels-Alder EXO IRC	Cheletropic IRC	Alternative Diels-Alder ENDO IRC	Alternative Diels-Alder EXO IRC
|	|	|	|	|

Table 8 visualises the IRC path of the Diels-Alder and Cheletropic reactions. Click on the links to see the animations.

Diels-Alder ENDO IRC	Diels-Alder EXO IRC	Cheletropic IRC	Alternative Diels-Alder ENDO IRC	Alternative Diels-Alder EXO IRC
[[1]]|	[[2]]|	[[3]]|	[[4]]|	[[5]]|

Table 7 and table 8 Shows the IRC (described in the Introduction section) of the reaction pathways of this exercise, including the movie file links that illustrates the nature of bond formations of the pathways. From the movies, it can be seen that all the Diels-Alder reaction pathways (including the reaction at the high energy site) form new bonds asynchronously. On the other hand, the bond formation of the cheletropic pathway is synchronous. It is worth noting that xylylene is an extremely reactive species, as it is only one oxidation state away from forming a 6-membered aromatic ring. In fact, this can be seen during the reaction of xylylene with sulphur dioxide (see the IRC animation), where the ring becomes aromatised when transition states are formed. This is not the case for the alternative pathway at the inner diene site, resulting in the reaction being highly unfavourable.

Thermochemistry

Table 9 shows the activation energies and Gibbs free energies of the different reaction pathways.

	Activation Energy / $kJmo{l}^{-1}$	Gibbs Free Energy / $kJmo{l}^{-1}$
DA ENDO	+84.4	-96.4
DA EXO	+88.4	-97.0
Cheletropic	+106.7	-153.4
Alternative DA ENDO	+114.7	+18.9
Alternative DA EXO	+122.5	+23.4

(This is really a change in free energy. Best to just call it a reaction energy Tam10 (talk) 14:42, 16 March 2018 (UTC))

Figure 11. The energy diagram illustrating the relative activation energies and Gibbs free energies of the Diels-Alder and Cheletropic reaction.

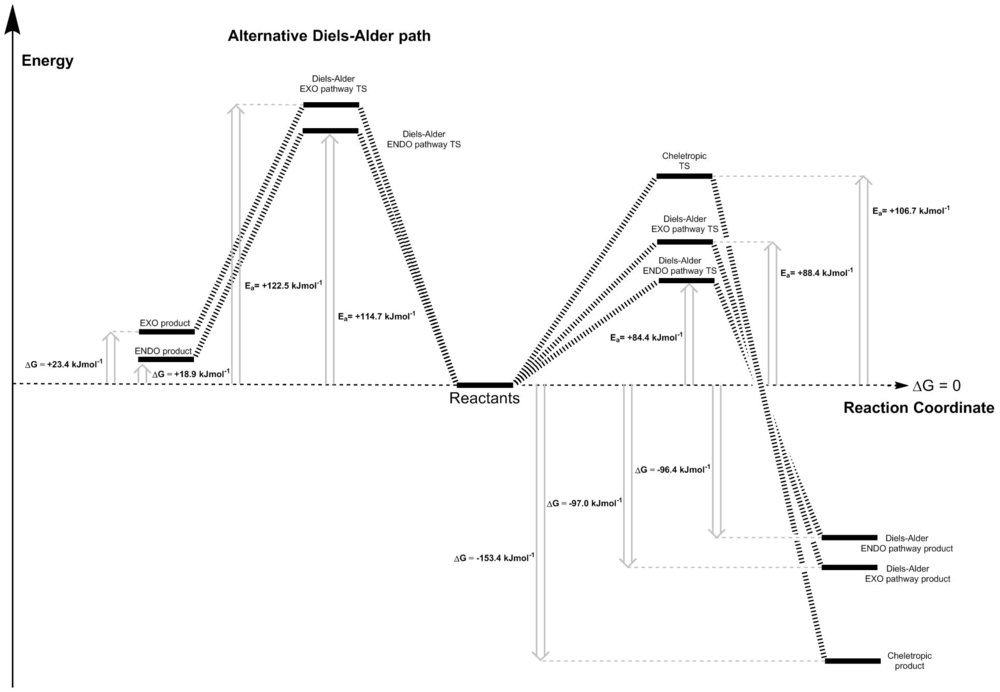
From figure 11, it can be seen that out of all the reaction pathways (excluding the alternative Diels-Alder), the cheletropic pathway has the greatest activation energy, making it the most kinetically stable compared to the other 2 pathways. One of the possible explanation for this is the fact that the reaction forms a new 5-membered ring, compared to 6-membered rings for the other pathways. The ring strain in the 5-membered ring raises the energy of the transition state, raising its activation energy. Even though it is the most kinetically inert compared to the other three, the cheletropic path is the most thermodynamically favourable, as it is the most exothermic pathway (most negative Gibbs free energy of reaction). This is because of the stabilisation of the product by the 2 strong S=O bonds (bond enthalpy of 518 kJ/mol each ) compared to only one S=O and one S-O (S-O contributes 348 kJ/mol ) in the Diels-Alder products. The two S=O bonds has a much greater effect than the ring strain in the 5-membered ring, making it the most exothermic reaction of the three.

Contrarily, the ENDO Diels-Alder pathway has the lowest activation energy, making it the fastest kinetically compared to the other two paths. This is due to the stabilisation of the transition state by secondary orbital interactions (similar to Exercise 2 case). This involves the interaction between the p orbital of the oxygen in sulphur dioxide and the delocalised π orbitals of xylylene. This is not possible for the EXO case as it does not have the correct geometry for the interaction, making its activation energy higher (but still lower than cheletropic path) than the ENDO transition state. Due to steric repulsions between the oxygen in the S=O and the rest of the molecule, the ENDO product energy is slightly above the EXO product. This makes the EXO path more thermodynamically favourable than the ENDO pathway, as it is slightly more exothermic. If the reaction is carried out under equilibrating conditions, the cheletropic product will be the major product of the reaction between sulphur dioxide and xylylene, as it is the most thermonamically favourable pathway.

The energy diagram (figure 11) shows that the alternative Diels-Alder reaction at the inner site is both thermodynamically and kinetically unfavourable. Firstly, the activation energy of the reaction is greater than any of the pathways described before. The reactions (EXO and ENDO) are endothermic, which means that they require energy to convert from reactants to product overall. The ENDO product here is both the kinetic and thermodynamic product compared to the EXO case. The transition states for this alternative pathway is higher in energy than the preferred path because it lacks the aromatic ring formed at the 6-membered ring. This also explains the why the reaction is endothermic, as the products does not have the aromatic 6-membered ring in it like the normal Diels-Alder and cheletropic products.

Extension: Electrocyclic reaction

Figure 12. The reaction scheme of the electrocyclic reaction of cyclobutene.

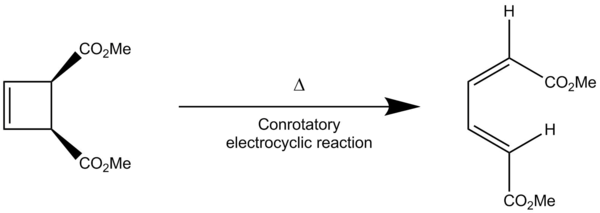
Corresponding Log Files

PS4615_EXT_CYCLOBUTENE_MIN_PM6.LOG

PS4615_EXT_CYCLOBUTENE_MIN_B3LYP.LOG

PS4615_EXT_TS_BERNY_PM6.LOG

PS4615_EXT_TS_BERNY_B3LYP.LOG

PS4615_EXT_TS_IRC_PM6.LOG

PS4615_EXT_PRODUCT_B3LYP.LOG

In this extension, the thermal electrocyclic ring opening of the molecule shown in the reaction scheme above was studied. Since electrocyclic reactions is a class of a pericyclic reaction, the stereochemistry of the product can be determined using the Woodward-Hoffman rules. From this, it was determined that the reaction undergoes conrotatory electrocyclic ring opening, which agrees with the calculations carried out using B3LYP (see the animation in table 10 and the vibrations of the transition state at figure 13). The activation energy of the reaction was found to be $+122.4kJmo{l}^{-1}$, with the Gibbs free energy of the reaction at $-64.1kJmo{l}^{-1}$. This shows that the reaction has a significantly high activation energy, making it kinetically inert. One possible explanation to this is the raise in the TS energy due to steric interactions between the bulky methyl ester groups during the transition from the reactant to product (see animations). Since the reaction is significantly exothermic, the reaction is considered thermodynamically favourable.

Figure 13 shows the vibration of the transition state.

Table 10 shows the IRC of the reaction, where the movie shows that the reaction is conrotatory.

The reaction's IRC
|
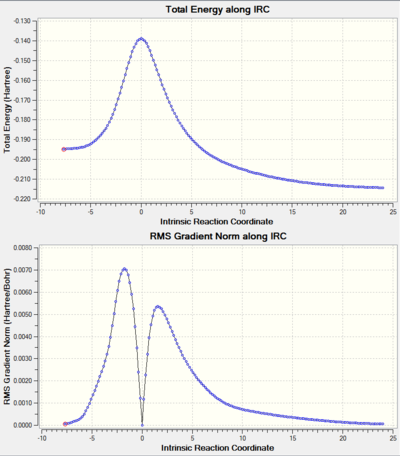IRC movie. Click on the link for movie.
[[6]]|

It is clear from the animations and the transition state vibrations that the reaction is a conrotatory electrocyclic ring opening. Aside from using the Woodward-Hoffmann rules, this can be determined and illustrated by looking the the HOMO of the reactants and products (see table 11). From the HOMO of the product, it can be seen that the only way that the reaction can proceed (working backwards) is through antarafacial interactions of the MOs at the terminal carbons, as this is the only way to achieve constructive interaction between the orbitals. In terms of the symmetry (when considering just the diene fragment), the HOMO is asymmetric. By following through with the reaction to the reactants, it can be seen that the terminal carbons rotate in the same direction to form the cyclobutene. This is illustrated in the in figure 14.

Figure 14. This illustrates the Frontier orbital (HOMO) approach to determining the stereochemistry of the reaction.

Table 11. The relevant molecular orbitals of the reaction.

Cyclobutene HOMO	Transition state HOMO	Product HOMO
Cyclobutene LUMO	Transition state LUMO	Product LUMO

(It is actually the HOMO-1 in the TS that has the orbitals that you are looking for Tam10 (talk) 14:49, 16 March 2018 (UTC))

Conclusion

In this experiment, a semi-empirical method PM6 and a hybrid method B3LYP were used to calculate the geometries and vibrations of 4 different transition states of 4 different pericyclic reactions successfully. Method three was used for all of the calculations, as it is the most accurate method out of the three. Starting with the first exercise, the C-C bond lengths involved in the reaction were analysed as the reaction progresses from the reactants, to the transition states and finally the product. It was also found that the bond formation is synchronous, which is not the case for the reactions in exercise 3. The activation energies and Gibbs free energies of the ENDO and EXO Diels-Alder reactions were calculated in exercise 2 up to the B3LYP level of accuracy. The relevant MOs were visualised to qualitatively show the effect of secondary orbital interactions and steric repulsions on the thermochemistry of the reactions. From the energies of the relavant MOs, it was proven that the Diels-Alder reaction in exercise 2 is an inverse electron-demand reaction. As for exercise 3, the different reaction paths were investigated for the reaction between sulphur dioxide and xylylene. It was found that the most thermodynamically favourable pathway is the Cheletropic path, whereas the ENDO Diels-Alder reaction path is the most kinetically driven. Lastly, calculations up to B3LYP level of accuracy for a thermal electrocyclic ring opening of cyclobutene was carried out. The IRC animation and the transition state vibrations showed that the reaction is conrotatory, which is in agreement with the Woodward-Hoffmann rules.