Rep:OJA300793

Computational Chemistry: Physical

Tutorial: Cope Rearrangement

Reactants and Products

Anti-periplaner vs Gauche

In order to establish which conformer of 1,5-hexadiene is the most stable, optmization calcualtions have been carried out on both a typical Anti-periplanar (app) and gauche conformer.

1,5 Hexadiene Anti-peri planar Configuration Optimization

Summary Table

1,5 Hexadiene Optimization
File Name	OJA_1_5_hexadiene_optimization_3
File Type	.chk
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.69253528 a.u.
RMS Gradient Norm	0.00001891 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group
Media:OJA_1_5_hexadiene_optimization_3.log

Point Group: C_i

Energy: -231.69254 a.u.

1,5 Hexadiene Gauche Configuration Optimization

Summary Table

1,5 Hexadiene Gauche Optimization
File Name	OJA_1_5_hexadiene_optimization_gauche
File Type	.chk
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.69266122 a.u.
RMS Gradient Norm	0.00000702 a.u.
Imaginary Freq
Dipole Moment	0.3405 Debye
Point Group
Media:OJA_1_5_hexadiene_optimization_gauche.log

Point Group: C₁

Energy: -231.69266

This data confirms that the Gauche conformer is more stable than the app one as it is lower in energy by 0.079kcal/mol. In comparison with the values given in the Tutorial Appendix it is clear that the reference conformer has been attained, and hence the lowest energy state of 1,5-Hexadiene, which has an energy of -231.69266 a.u.

When considering the Newman Projections, displayed below, of the two conformers it would be expected that the app conformer would be lower in energy due to a lack of steric interactions. However the distance between the two -CH=CH2 must be within the 'attractive' range of the two so by being gauche to one another there are in fact attractive forces between them, making the gauche conformer more stable. The through space bonding between the carbons on the two CH-CH₂ groups have been tabulated below. The maximum attractive force between two carbons is at 3.2Å, and all bar one of these distances are greater than 3.2A meaning they are attractive. However some argue that the fact that the difference in energy of the conformers means it is impossible to establish a single one as the universal minima for the molecule

Newman Projections

App	Gauche

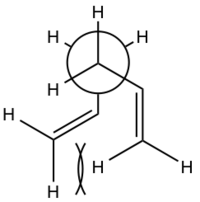
1,5 Hexadiene App Opt 631G(d)

Summary Table

1,5 Hexadiene App Optimization
File Name	OJA_1_5_hexadiene_optimization_app_631Gd
File Type	.chk
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(D)
Charge	O
Spin	Singlet
Total Energy	-234.61170280 a.u.
RMS Gradient Norm	0.00001326 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group
Media:OJA_1_5_hexadiene_optimization_app_631Gd.log

Point Group: C_i

By using a more advanced basis set a more accurate picture of the molecule can be obtained. The app has retained its symmetry, with both structures having C_i point group. To the naked eye the strucutres are the same but on closer inspection differences can be seen. For example corresponding bond lengths and angles are not identical across the two, as tabulated below. Although these differences are only small it demonstrates the affect of using a more advanced basis set.

Basis Set	C1-C2	C2-C3	C3-C4	C4-C5	C5-C6	C1-Ĉ2-C3
3-21	1.316Å	1.509Å	1.553Å	1.509Å	1.316Å	124.8
6-31G*	1.334Å	1.504Å	1.548Å	1.504Å	1.334Å	125.3

In order to establish that a molecule has been optimised to a minima it is important to carry out a vibrational analysis on the optimised structure. If a minima has been achieved then all frequencies should be real, i.e none will be negative. A frequency analysis was carried out on 1,5-hexadiene using the 631G* structure.

1,5 Hexadiene App Frequency

Summary Table

1,5 Hexadiene App Frequency		IR Spectrum
File Name	OJA_1_5_hexadiene_optimization_app_Freq
File Type	.log
Calculation Type	Freq
Calculation Method	RB3LYP
Basis Set	6-31G(d)
Charge	0
Spin	Singlet
Total Energy	-234.61171021 a.u.
RMS Gradient Norm	0.00001497 a.u.
Imaginary Freq	0
Dipole Moment	0.0000 Debye
Point Group	CI
Media:OJA_1_5_hexadiene_optimization_app_Freq.log

Point Group: C_i

In the table above the IR spectrum can be seen, which shows all real frequencies only, therefore this structure is a minima. Below the Thermochemistry data for the molecule has been extracted from the calculation file.

Thermochemistry

Sum of electronic and zero-point Energies= -234.469204
Sum of electronic and thermal Energies= -234.461857
Sum of electronic and thermal Enthalpies= -234.460913
Sum of electronic and thermal Free Energies= -234.500778 

Transition States

In the Cope Rearrangement there are two transition states, the chair and the boat. In this exercies both will be optimised and evaluated in order to build a better picture of what happens in the reaction.

Chair Transition State

Summary Table

Chair TS Optimization & Frequency		Vibration
File Name	OJA_Chair_TS_Guess_1
File Type	.chk
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.61932246 a.u.
RMS Gradient Norm	0.00000727 a.u.
Imaginary Freq	1
Dipole Moment	0.0003 Debye
Point Group		Imaginary Frequency is at -817.94 cm-1
Media:OJA_Chair_TS_Guess_1.log

By combining optimisation and frequency only 1 calculation needs to be run through Gaussian. As can be seen by the animation above this imaginary frequency firstly shows that this structure is a minimum and secondly that this is how the transition state develops towards the product.

There is more than one way of optmising a transition state and the Bond Freeze method has been used below.

Chair Transition State Bond Freeze Opt

Summary Table

Chair TS Bond Freeze Optimization
File Name	OJA_Chair_TS_bond_freeze_2_berny
File Type	.log
Calculation Type	FTS
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
E(RHF)	-231.61932239 a.u.
RMS Gradient Norm	0.00002349 a.u.
Imaginary Freq
Dipole Moment	0.0005 Debye
Point Group	C1
Media:OJA_Chair_TS_bond_freeze_2_berny.log

On direct inspection the two structures found look very similar and have similar energies. A table below shows the bond breaking/forming bond lengths in the molecules. As the values are the same it shows that both of these methods are valid when optimising the transition state.

Structure	Bond Forming	Bond Breaking
Opt&Freq	2.021 Å	1.389 Å
Bond Freeze	2.021 Å	1.389 Å

Carbon	Bond Distance
	Opt & Freq	Bond Freeze
C3 - C14	2.02051Å	2.02064Å
C6 - C11	2.02051Å	2.02064Å

Boat Transition State

In order to optimise the boat transition structure it must be in a geometry similar to the optimised structure before the calculation is carried out. When attempted in a linear chain form the calculation failed, and only ran when the molecules were manipulated to resemble a 'C' did the calculation run.

Summary Table

Boat TS Optimization & Frequency		Vibration
File Name	OJA_Boat_TS_Opt_Freq_Finally
File Type	.chk
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.60280247 a.u.
RMS Gradient Norm	0.00001668 a.u.
Imaginary Freq	1
Dipole Moment	0.1583 Debye
Point Group		Imaginary Frequency is at -840.03 cm-1
Media:OJA_Boat_TS_Opt_Freq_Finally.log

Chair IRC

Summary Table

Chair IRC
File Namecell	OJA_Chair_TS_IRC_4
File Typecell	.log
Calculation Type cell	IRC
Calculation Methodcell
Basis Setcell
Charge cell	0
Spincell	Singlet
E(RHF)cell	-231.61932246 a.u.
RMS Gradient Normcell	0.00000728 a.u.
Imaginary Freqcell
Dipole Momentcell	0.0003 Debye
Point Groupcell	C1
Media:OJA_Chair_TS_IRC_4.log

On the link below a video of the IRC can be found.

File:OJA Chair TS TO PRODUCT.m4v

However the IRC doesn't confirm which final structure has been formed so an optimisation to a minimum was carried out on the final structure given.

Summary Table

IRC Structure Optimization
File Name	OJA_Chair_IRC_Final_Structure_Opt
File Type	.chk
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
E(RHF)	-231.69166702 a.u.
RMS Gradient Norm	0.00000475 a.u.
Imaginary Freq
Dipole Moment	0.3806 Debye
Point Group	C1
Media:OJA_Chair_IRC_Final_Structure_Opt.log

From this it can be seen that Gauche conformer has been formed, and by comparing the energies given in Appedix 1 on the tutorial sheet is between Gauche 2 and Gauche 4. Although this is not the most accurate way of establishing the conformer it is quick and is good to use as an approximation.

Reoptimization of Chair And Boat

Summary Table

Chair TS Reoptimization & Frequency
File Name	OJA_Chair_TS_ReOpt_freq
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(D)
Charge	O
Spin	Singlet
E(RB3LYP)	-234.55698295 a.u.
RMS Gradient Norm	0.00002879 a.u.
Imaginary Freq	1
Dipole Moment	0.0003 Debye
Point Group	C1
Media:OJA_Chair_TS_ReOpt_freq.log

Summary Table

Boat TS Reoptimization & Frequency
File Name	OJA_Boat_TS_ReOpt_freq
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(D)
Charge	O
Spin	Singlet
E(RB3LYP)	-234.54309366 a.u.
RMS Gradient Norm	0.00008351 a.u.
Imaginary Freq	1
Dipole Moment	0.0612 Debye
Point Group	C1
Media:OJA_Boat_TS_ReOpt_freq.log

Summary Table

Below is a compilation of all the Energy data collected across the calculations run in this exercise for the Reactants and Char and Boat Transition structures for the Cope Rearrangement. These are in line with those given in Appendix 2 of the Tutorial.

in a.u.

Molecule	HF/3-21G			B3LYP/6-31G*
	Electronic Energy	Sum of Electronic and Zero-Point Energies (0K)	Sum of Electronic and Thermal Energies (298.15K)	Electronic Energy	Sum of Electronic and Zero-Point Energies (0K)	Sum of Electronic and Thermal Energies (298.15K)
Reactant (App)	-231.69253528	-231.539539	-231.532565	-234.61171021	-234.469204	-234.461857
Chair TS	-231.61932246	-231.466701	-231.461341	-234.55698295	-234.414932	-234.409011
Boat TS	-231.60280247	-231.450930	-231.445301	-234.54309366	-234.402347	-234.396012

in kcal/mol

Molecule	HF/3-21G		B3LYP/6-31G*
	(0K)	(298.15K)	(0K)	(298.15K)
ΔE (Chair)	45.71	44.69	34.06	33.16
ΔE (Boat)	55.60	54.76	41.95	41.32

Diels Alder Reaction

Butadiene

Summary Table

Butadiene Optimization & Frequency
File Name	OJA_Butadiene_Opt_Freq
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d)
Charge	0
Spin	Singlet
E(RB3LYP)	-155.98595614 a.u.
RMS Gradient Normc	0.00002726 a.u.
Imaginary Freq	1
Dipole Moment	0.0854 Debye
Point Group	CS
Media:OJA_Butadiene_Opt_Freq.log

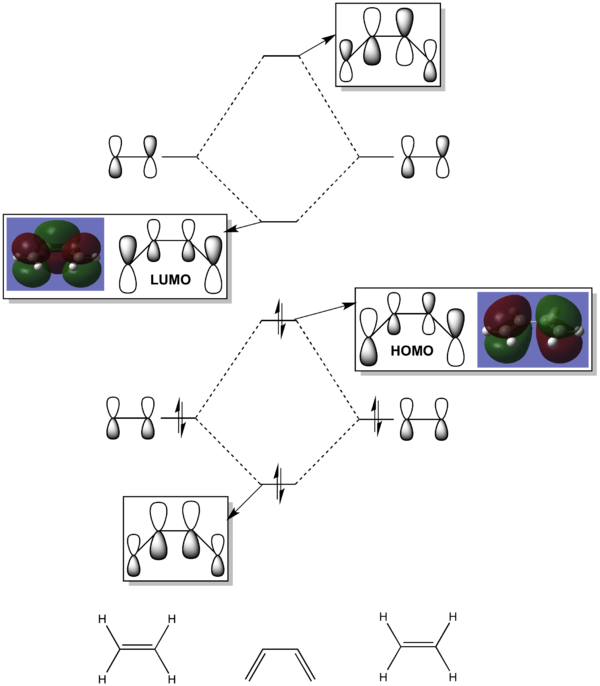
From this structure the HOMO and LUMO have been plotted, as shown below.

Butadiene Molecular Orbitals
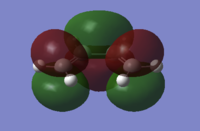HOMO, asymmetric with respect to the plane, a	LUMO, symmetric with respect to the plane, s

A sketch of the MOs has been made for ease of interpretation. The π orbitals are very distinct in the Gaussian MOs and the orbital contributions can clearly be seen; carbons 2 and 3 contribute less than 1 and 4 hence their smaller orbitals.

Transition State

The transition state for a Diels Alder reaction between Butadiene and Ethene was constructed and optimised using TS(Berny) and calculating the Force Constants Once. This method was used after failing to run a TS(QST2) calculation due to a lack of similarity of structures submitted against the actual transition state minima.

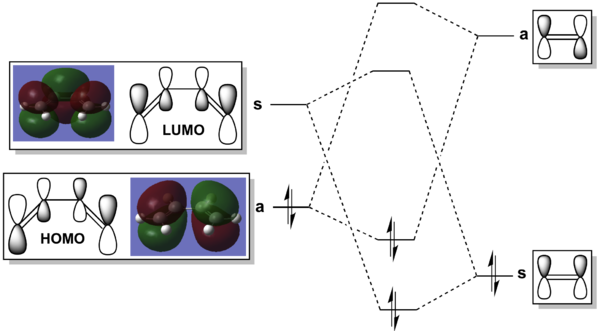
A frontier orbital molecular orbital diagram of butadiene and ethene can be seen below. This transiotn is allowed due to the mathcing orbital symmetry for Ethene(LUMO)-Butadiene(HOMO) and Ethene(HOMO)-Butadiene(LUMO) denoted by an s (symmetric) and an a (asymmetric) with respect to the plane on the MO diagram.

Summary Table

Diels Alder TS Opt&Freq
File Name	OJA_DA_TS_Guess_8
File Type	.chk
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d)
Charge	0
Spin	Singlet
E(RB3LYP)	-234.54389655 a.u.
RMS Gradient Normc	0.00000182 a.u.
Imaginary Freq	1
Dipole Moment	0.3942 Debye
Point Group
Media:OJA_DA_TS_Guess_8.log

Figure 1

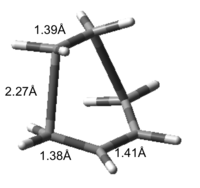
This structure can be confirmed as a transition state due to the presence of a single imaginary frequency at -525cm^-1 which matches the proposed mechanism of the Diels Alder Reaction. The formation of the two bonds is synchronous, as shown by the vibration, however the lowest 'real' frequency of the molecule is an asynchronous twist of the ethene molecule, giving an obvious distinction between the 'reacting' vibration and the real one.

The partially formed C-C σ bonds in the transition state have a length of 2.27Å, which is in accordance with literature values found. This value is larger than both sp³ and sp² carbon bonds (1.54Å and 1.47Å respectively) but is smaller than the sum of Carbons van der Waals Radii (3.4Å, 1.7Å per carbon) indicating that a bond is in the process of forming and this inter atomic distance will contract as shown in the vibration above.

The bond lengths of the other carbon bonds can be seen in Figure 1.

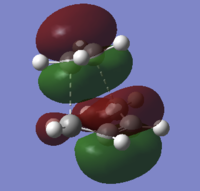
On inspection of the HOMO of the Transition State it can be seen to be made up of a mix of π and sp3 orbitals as certain π bonds break and the orbitals hybridise to sp³ orbitals. The fact that the symetrical homo-π orbitals of ethene are seemingly intact in the transtion state it can be specualted the the transition state HOMO is the combination Ethene(HOMO)-Butadiene(LUMO). From the MO diagram at the beginning of this section, this combination does not produce the HOMO of cyclohexene indicating that this orbital once reacted will lower itself in energy below the Ethene(LUMO)-Butadiene(HOMO) combination. The LUMO, as predicted in the MO is a combination of Ethene(HOMO)-Butadiene(LUMO) but inverted. A sketch along with the calculated MO diagrams can be found in the table below.

Transition State Molecular Orbitals
HOMO, s	LUMO, s

Cyclohexa-1,3-diene & Maleic Anhydride

In order to determine the transition states in the Diels Alder reaction between Cyclohexa-1,3-diene and Maleic Anhydride, the reactants and products were optimised for comparative purposes. The optimised reactant structures were then used in order to assemble the 'guess' transition states before they were optimised.

Reactants Summary Table

	Cyclohexa-1,3-diene Optimization	Maleic Anhydride Optimization
File Name	OJA_Cyclohexa13_Opt	OJA_MaleicAnhydride_Opt
File Type	.chk	.chk
Calculation Type	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP
Basis Set	6-31G(D)	6-31G(D)
Charge	0	0
Spin	Singlet	Singlet
Total Energy	-233.41891004 a.u.	-379.28954412 a.u.
RMS Gradient Norm	0.00013317 a.u.	0.00011730 a.u.
Imaginary Freq
Dipole Moment	0.3785 Debye	4.0749 Debye
Point Group
log File:	Media:OJA_Cyclohexa13_Opt.log	Media:OJA_MaleicAnhydride_Opt.log

Products Summary Table

	Diels Alder Endo Product Optimization	Diels Alder Exo Product Optimization
File Name	OJA_DA_Pr_Exo	OJA_DA_Pr_Endo
File Type	.fch	.fch
Calculation Type	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP
Basis Set	6-31G(D)	6-31G(D)
Charge	0	0
Spin	Singlet	Singlet
Total Energy	-612.75578531 a.u.	-612.75829018 a.u.
RMS Gradient Norm	0.00003162 a.u.	0.00001678 a.u.
Imaginary Freq
Dipole Moment	4.7592 Debye	5.0202 Debye
Point Group
D-Space	DOI:10042/25964	DOI:10042/25963

The transition states were optimised to TS(Berny) with force constants calculated once, as in the Diels Alder reaction between Butadiene and Ethene. The Imaginary Frequencies can be seen below the summary table and show the breaking and forming of the bonds in the transition of the reaction.

Transition States Summary Table

	Diels Alder TS Exo Opt&Freq	Diels Alder TS Endo Opt&Freq
File Name	OJA_DA_TS_Exo_2	OJA_DA_TS_Endo_1
File Type	.fch	.fch
Calculation Type	FREQ	FREQ
Calculation Method	RB3LYP	RB3LYP
Basis Set	6-31G(D)	6-31G(D)
Charge	0	0
Spin	Singlet	Singlet
Total Energy	-612.67931094 a.u.	-612.68339675 a.u.
RMS Gradient Norm	0.00001057 a.u.	0.00001893 a.u.
Imaginary Freq	1	1
Dipole Moment	5.5504 Debye	6.1143 Debye
Point Group
D-Space	DOI:10042/25967	DOI:10042/25968

Imaginary Frequencies
Exo, -448cm-1	Endo, -447cm-1

Figure 2

The comparitve energy to the reactants has been tabulated with the exo transition state requiring a greater amount of energy. This reaction is kinetically controlled meaning that the endo product will be favoured as the major product. This is well represented by the reaction coordinate in Figure 2, the blue line is the Endo formation and the red line is the exo formation.

Isomer	ΔE
Exo	18.32 kcal/mol
Endo	15.75 kcal/mol

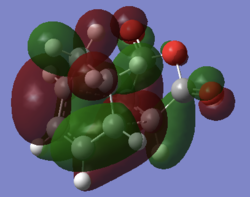
Although there is only a relatively small difference in activation energy for the two transition states there will be a large difference in products formed due to the exponential relationship between energy and rate in the Arrhenius equation. The lower activation energy for the Endo transition state can be put down to secondary orbital interactions. This is where the carbon π orbital on the Anhydride -C=O interacts with the carbon π orbital in the diene in a positive way to stabilise the whole molecule. There is a through space bond distance of 3Å, which is less than the sum of the van der waals radii of two carbon atoms, meaning that the two orbitals are close enough to interact. This stabilisation is lost in the exo structure as the Anhydride π orbital cannot interact with the sp³ orbital of the carbon it is opposite due to a lack of matching orbital symmetry despite being within the sum of the van der Waals raddii. This indicates that this interaction is a potentially repulsive one, hence the higher activation energy required to reach this state.

On inspection of the HOMOs of the two transition states the SOI can definitely be seen in the endo structure, with a mass of electron density centred between the double bond in the diene and the maleic anhydride

HOMO Molecular Orbtials

Exo	Endo
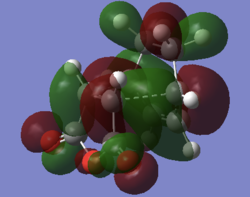a	a

Bond Lengths
Exo	Endo