Rep:Namespace:jr4073
Computational Chemistry - Introduction and application...
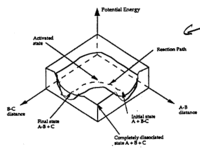
Computational chemistry allows us to model transition states and potential energy surfaces to predict reactivity, which has many applications, illustrated here with the Cope rearrangement and Diels Alder cycloaddition reactions.
Modelling Techniques & Calculations
The computational models may be built from ChemDraw structural drawings, which convert to 3D structures in Chem3D, or by direct modelling in GaussView. Optimisations may be run by MM2 (molecular mechanics) or PM6 (semi-empirical molecular orbital theory) in Chem3D. The principale method here is the use of Gaussian to run molecular orbital-based quantum calculations - numerically solving the Schroedinger equation - giving a more accurate result.
Computational Chemistry - Module 3: Physical
The first section of this investigation illustrates the virtues of computational methods in determining transition states, using the Cope Rearrangement as an example. The mini-project that follows then applies these methods to deduce new conclusions.
Cope Rearrangement

Computational methods are used to investigate transition states (potential energy minima) for the Cope rearrangement of 1,5-hexadiene to determine the preferred mechanism (step-wise, dissociative or concerted). This is begun with a conformational analysis of the reactants before considering transition state geometry (chair or boat).
Conformational analysis of hexadiene
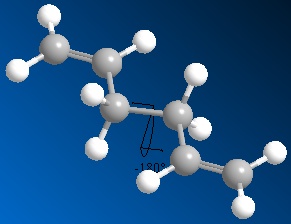
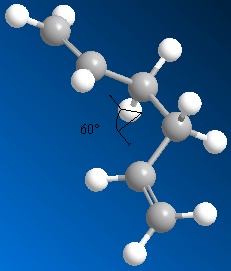

Molecules may exist in various conformations, of differing energies. For substituted carbons these may be termed depending upon the arrangement of substituents relative to each other, this is illustrated below by Newman projection.
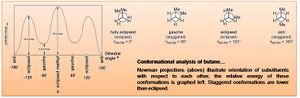
1,5-hexadiene has been geometry optimised in Gaussian (method: Hartree-Fock [HF]; basis set: 3-21G) for both the anti and gauche conformation (of the central four C atoms); the %mem term has been set at 250MB and 500MB for both calculations, showing no difference in the results. The energy and symmetry (point group) of the optimised structures are tabulated below. One would expect the gauche conformation to be at a higher energy, and this is the initial result. However, a number of possible gauche structures can be imagined, and these have also been optimised, identifying a gauche conformation at lower energy than the anti, which match the reference structures (https://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3#Appendix_1). This is a result of the gauche conformer increasing the entropy of the system, which is favourable.
The initial anti and gauche conformations are shown right (click to enlarge; links to 3D JMols).
- Note: the numbering of gauche conformations in the table below does not intend to correspond with the numbering on the reference table

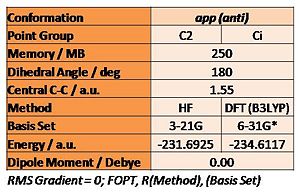
A further anti conformation has been modelled also, shown right. The Ci (symmetry) anti2 conformation of 1,5-hexadiene has been optimised at both the HF/3-21G and B3LYP/6-31G* level, the energies are tabulated below. There is essentially no difference between the geometry of the two structures, but a large difference in energy.
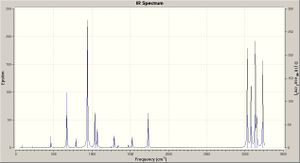
Vibrational analysis confirms the structures to be minimal energy (vibrational frequecies are the second derivative of energy, being real and positive thus corresponds to a minima point). For the higher level calculation, the 'low frequencies' are:
Low frequencies --- -9.4888 -0.0006 -0.0006 0.0002 3.7552 13.0176 Low frequencies --- 74.2853 80.9980 121.4178
The infrared spectrum is shown right. The vibrational analysis also computes real properties that may be compared:
Sum of electronic and zero-point Energies= -234.469204 Sum of electronic and thermal Energies= -234.461857 Sum of electronic and thermal Enthalpies= -234.460913 Sum of electronic and thermal Free Energies= -234.500777
The first of these is the potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE), the second is the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + Evib + Erot + Etrans), the third contains an additional correction for RT (H = E + RT) which is particularly important when looking at dissociation reactions, and the last includes the entropic contribution to the free energy (G = H - TS).
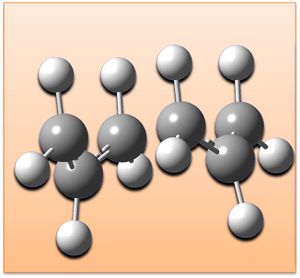
Optimising the chair and boat transition structures
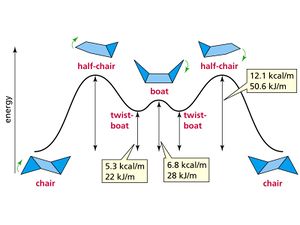

The chair and boat conformations of cyclohexane are illustrated right (also showing their relative energies), as transition states the atoms are in these arrangements with bond being made and broken.
Optimisation to a TS (Berny; chair)
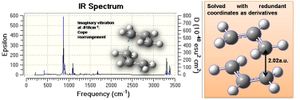
Initially the delocalised allyl fragment (CH2CHCH2) was optimised (HF/3-21G) and configured in the assumed chair transition state (terminal C's approx. 2.2a.u. apart): this is shown right. A vibrational analysis was performed, revealing an imaginary vibration at 818cm-1 corresponding to the Cope rearrangement - this is shown below; the optimised transition state structure is shown right, with a distance of 2.02a.u. between the terminal carbons of each fragment.
Frozen coordinate method (chair)
The transition state optimisation was repeated with frozen coordinates (the bond distance between the terminal carbons fixed), this was then repeated with the frozen coordinate bond as a derivative (no force constants calculated). The optimised lengths of the bond forming/breaking is retained at 2.02a.u. This corresponds to the chair transition state, with the same appearance as that of the TS (Berny) method, shown right.
QST2 method (boat)

The boat transition state is optimised by the QST2 method: specifying the reactant and product structures, with the calculation interpolating between the two; crucial to this is a numbering of the carbons in the reactant and product that match. This method is not possible with the anti conformer of the reactant as rotation about the central bond is not possible and a transition state corresponds not to the Cope rearrangement. However, adjusting the reactant geometries allows for a boat transition state. This is illustrated below.
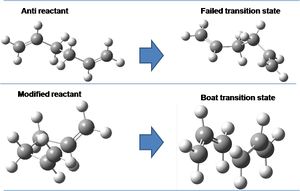
The bottom carbons of the fragments are separated 'through space' by 2.14a.u., CC distances in the fragments 1.38a.u.; the further apart carbons at the top of each fragment are separated by 2.78a.u. through space.
Intermediate reaction coordinate analysis

The optimised chair and boat transition structures connect conformers of 1,5-hexadiene, though by visual inspection it is nearly impossible to tell which ones. This is determined instead by following the minimum enery path from the transition state down to the local minimum (reactants) on a potential energy surface (intrinsic reaction coordinate [IRC] method in Gaussian).
Force constants have been determined once at the beggining of the calculation, running the reaction coordinate in just the forward direction (since this is symmetrical), with 50 points. Initially a minimum is not reached (the gradient does not fall to zero - see graph, right), leaving three options:
- take the last point on the IRC and run a normal minimization (may lead to a local minima)
- restart the IRC and specify a larger number of points until it reaches a minimum (if not enough points, again a local minima)
- redo the IRC specifying to compute the force constants at every step (expensive and infeasible for large systems)
The third option has been implemented, revealing the chair to result from conformer gauche 2 (see reference table: https://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3) and the boat from a rather higher energy totally eclipsed conformer, resembling that used for the modified QST2 calculations above (a minimum was not achieved here, even using 100 iteration points).
The reaction coordinate paths for the chair and boat transition states are illustrated below.

Higher level optimisation to determine activation energies & discussion

The chair and boat transition structures have been reoptimised at the higher B3LYP/6-31G* level of theory, these are shown right with links to 3D JMols (note these return the structure to a localised bonding representation). The energies of the transition structures are both levels of theory are tabulated below and activation energies calculated, at the higher level of theory these are in fair aggreement with the experimental values (0K) when accounting for error, being no more than 1 kcal/mol out.

A geometry analysis has also been performed, investigating the through space separation of the fragments in the transition state, and C-C bond lengths within the fragments at the different levels of theory. These are tabulated (and illustrated) below.
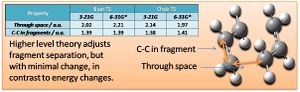
In summary the geometry changes minimally at the higher level of theory, while the molecules are greatly stabilised and found to have much lower energies (more accurate also, being a better agreement with experimental data for activation energy).
It is concluded that under kinetic control the reaction will proceed via the chair transition state as this has the lower activation energy.
Mini-Project
A mini-project in transition state computational chemistry has been conducted based on the Diels-Alder cycloaddition.
The projects should be viewed here: https://www.ch.ic.ac.uk/wiki/index.php/Namespace:jr4073PROJECT.
Error analysis...
Calculated energies are accurate to ~10kJ/mol; dipole moments are accurate to 0.01 Debye, and frequencies reported to 1cm-1 (typically 10% error), likewise intensities (infrared) are given as whole numbers; bond distances are accurate to 0.01a.u. and angles to 0.1deg.
Notably energies between molecules should only be considered on a relative (kJ/mol; not absolute!) level; absolute values are noted for reproducibility only (a.u.), and consistency is paramount for comparison (basis set, method, details).
References
External links
- [Michigan Engineering College - Transition State Theory: http://www.engin.umich.edu/]
- [Chemistry SCAN Link: https://scanweb.cc.imperial.ac.uk/uportal2/]
- [Illustration of vibrational mode categories: http://en.wikipedia.org/wiki/Infrared_spectroscopy]
- [Online symmetry point group flow chart: http://capsicum.me.utexas.edu/ChE386K/Images/point_group_flowchart_shriver.jpg]
- [Mini-project: https://www.ch.ic.ac.uk/wiki/index.php/Namespace:jr4073PROJECT]
