Rep:Mpg15TSReport

Introduction

Potential Energy Surfaces

Figure 1: Plot illustrating a PES

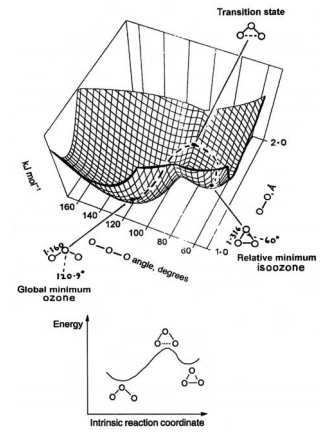
The basic concept behind optimisation calculations in computational chemistry is the Potential Energy Surface. It is a multi-dimensional plot showing the changes in energy of the system being studied as a function of the spatial configuration of its constituent atoms. A non-linear molecule has 3N-6 degrees of freedom, so a surface that follows the energy changes along each possible geometric coordinate will have 3N-6 dimensions. Different geometries of the molecule will have different potential energies, and as such, will correspond to different points on this surface. These points can be minima, maxima or saddle points. A minimum on an energy surface represents a stable molecular configuration. These can be local or global, corresponding to various possible species that can form within the reaction, such as the reactants, products or stable intermediates. Since the PES has many dimensions, the minima are defined in terms of the derivatives of the energy (E) against distance in all directions (r): $(\frac{\partial E}{\partial r}=0)$ and $(\frac{{\partial }^{2}E}{\partial r^{{}^2}}>0)$. This second derivative is also equivalent to a force constant k, and therefore corresponds to a vibration of the molecule. . The calculations of these sets of second differentials are carried out using a Hessian matrix. It is the solution of this matrix that underpins all of computational calculations carried out in this lab.

The transition state on a PES is a maximum linking two minima. If the minima involved are the reactants and products, the highest point directly between them is the transition state of the reaction. Mathematically, this is calculated much like the minimum, with the first derivative equal to zero in all directions, and the second derivative being positive in all directions but one. Along the coordinate which links the two minima, the second derivative is negative, indicating a maximum. This means the transition state can be confirmed by the presence of a single negative vibration, which is given by a negative (imaginary) force constant.

Nf710 (talk) 09:07, 6 March 2018 (UTC) This is correct. You obtain this info by diagonalising the Hessian Matrix its eigen values at the zero gradient geom are the force constants and the eigenvectors of this eiegn pair are the normal mode which are linear combinations of the degrees of freedom.

Computational Methods

To calculate the energy surface, we use the Born-Oppenheimer approximation, which states that atomic nuclei are stationary relative to the electrons. We can then solve the Schrödinger equation and calcuate the Hamiltonian for the system. To do this we must construct the electronic wavefunctions for the system being studied. We approximate these using a Linear Combination of Atomic Orbitals, which takes the atomic orbitals as a basis set, and scales them to build up representations of the molecular orbitals, which are then integrated to compute the energy of the system.

The two computational methods used - PM6 and B3LYP - differ in the method which they use to compute the hamiltonian. PM6 is a semi-empirical method, which uses the Hartree-Foch approach to calculate the Hamiltonian. It does not directly compute the integrals involved in the Hamiltonian. Instead, it uses pre-existing experimentally obtained values to approximate these, which saves computational time but reduces accuracy of the calculated energies. B3LYP is a density functional theory method, which also uses the Hartree-Foch approach, but instead calculates the integrals numerically, which gives much more accurate results, but takes significantly longer.

Nf710 (talk) 09:09, 6 March 2018 (UTC) Good understanding. You could have gone into some detail about the basis sets and possibly added some equations to aid your discussion.

Exercise 1: Reaction of Butadiene with Ethylene

(Fv611 (talk) This section was very well done. Good job!)

The reaction carried out was the Diels-Alder cycloaddition of butadiene and ethylene. All calculations were carried out at the PM6 level.

Figure 2: Cyclohexene Formation

MO Diagram

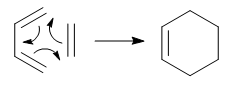
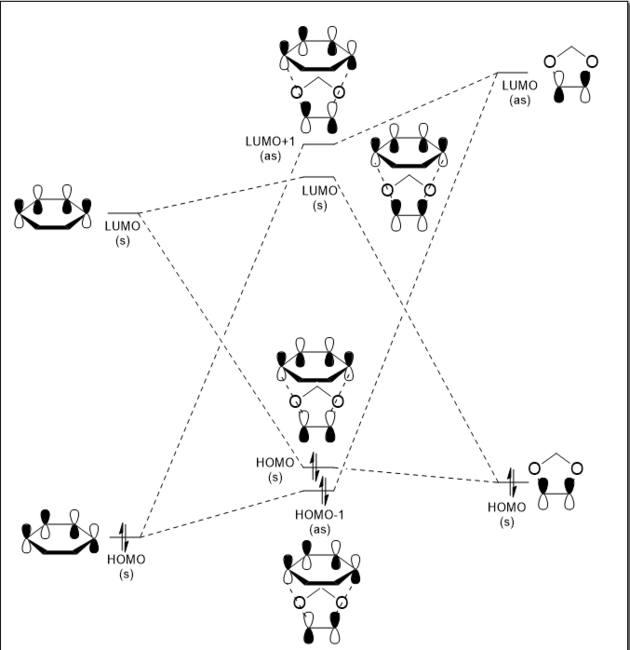
Figure 3: Diels-Alder Transition State MO Diagram

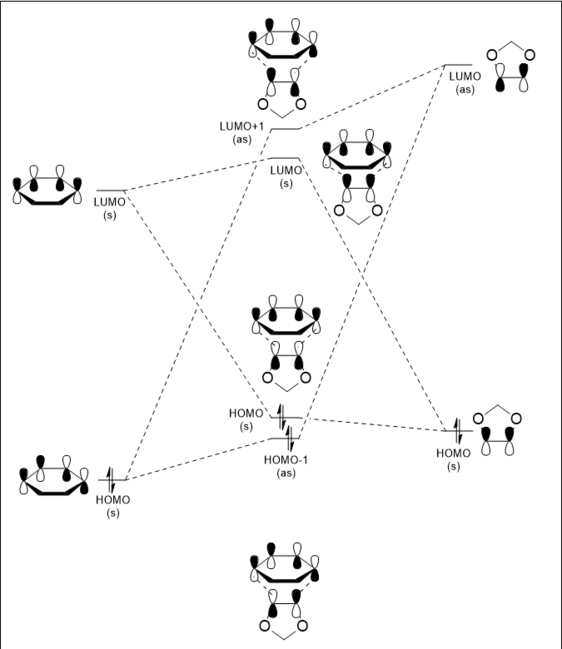
The MO diagram shows a schematic representation of the interacting MOs in the formation of the transition state of the reaction. These are visualized in 3D in the table below. The reaction proceeds with interactions between the HOMO and LUMO MOs of both molecules, with symmetric MOs combining together, and antisymmetric MOs combining together. The orbitals that form are of a higher energy due to the fact the transition state is a point of maximum energy along the reaction coordinate. The JMol visualizations for the transition state HOMO and LUMO+1 are lacking a set of P orbitals on the carbon atoms on the ends of the butadiene. This is a result of the approximations taken by the PM6 calculation method - there is in fact a bonding/antibonding interaction between the two molecules which involves these P orbitals, as indicated on the MO diagram. To visualise these more accurately, the TS optimisation could be repeated using the B3LYP method.

The symmetry of the interacting MOs indicates the value of the overlap integral. The overlap integral is the measure of the space shared by two molecular orbitals, calculated using the following equation: ${\mathbf{S}}_{\mathrm{A}\mathrm{B}}=\int {\mathrm{\Psi }}_{\mathrm{A}}^{*}{\mathrm{\Psi }}_{\mathrm{B}}dV$.
This integral will be equal to zero if the wavefunctions involved are orthogonal to one another, or if they have positive and negative components which cancel one another out. Therefore in the case of this reaction, the overlap integral will be non-zero for the interactions of symmetric orbitals with symmetric orbitals and the interactions of antisymmetric orbitals with antisymmetric orbitals. It is zero when antisymmetric orbitals interact with symmetric orbitals, which is why no such interactions are visible on the MO diagram and in the 3D visualizations.

Ethene	Butadiene	Transition State
Ethene HOMO	Butadiene HOMO	TS HOMO (See Discussion)	TS HOMO -1
Ethene LUMO	Butadiene LUMO	TS LUMO	TS LUMO +1 (See Discussion)

Bond Lengths and Transition State

Figure 4: Numbering of C atoms used in bond length calculation

Figure 5: Plot of C-C bond lengths vs reaction coordinate

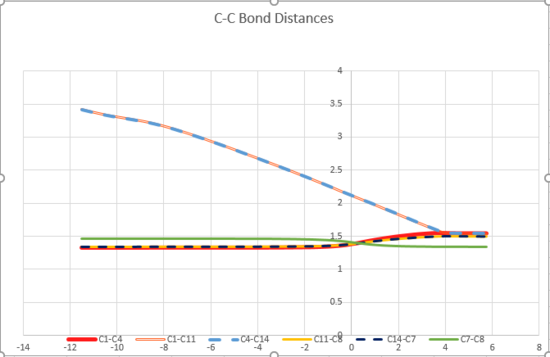
A qualitative look at the change of C-C bond lengths (Figure 5) shows that three shorter C=C bonds extend over the course of the reaction to longer C-C bonds, the single C-C bonds shortens to a C=C bond, and two new C-C bonds form between the two reactant molecules. This is exactly what we would expect from this reaction.

C-C Pair	Reactants	Transition state	Product
C1-C4	1.327	1.382	1.541
C1-C11	3.414	2.115	1.54
C4-C14	3.414	2.115	1.54
C11-C8	1.335	1.38	1.501
C14-C7	1.335	1.38	1.501
C7-C8	1.468	1.411	1.338

The values for carbon-carbon bond lengths given in the literature are as follows: C-C: 1.54Å C=C: 1.34Å The Van der Waals radius for a carbon atom is: 1.70Å A closer analysis of the C-C bond lengths shows that the bonds in the product and reactants match the literature values closely. The single C-C bond in the butadiene is somewhat shorter than expected, which suggests a degree of conjugation across the molecule giving the bond partial C=C character. In the transition state, the C-C bonds are distorted from their equilibrium lengths as expected, with C=C bonds lengthening and the C-C bond shortening. In all cases, the lengths of the Transition state bonds are closer to those of the reactants than the products. This suggests that, according to Hammond's Postulate, the reaction proceeds via an early transition state. The intermolecular C-C distance between the reactants is greater than the sum of the Van der Waal radii as expected. In the transition state, it is significantly lower, indicating orbital overlap and the beginning of some bonding interactions.

Figure 6: Vibration illustrating Diels-Alder Transition State

The vibration visualised in Figure 6 shows the imaginary vibration frequency associated with the transition state. It clearly shows the formation of the two new C-C bonds is synchronous, as expected for a Diels-Alder reaction and as indicated by the C-C bond distance plot in figure 5.

IRC

IRC Animation	IRC Profile

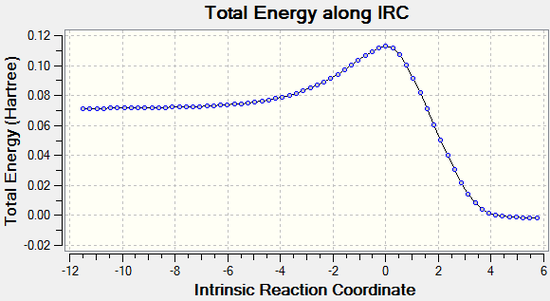
The animation above again illustrates the synchronous bond formation. (Click to play)

Additional LOG Files

File:Mpg15 PROD OPT.LOG

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Figure 7: Endo And Exo Reactions for cycloaddition of 1,3 dioxole and cyclohexadiene

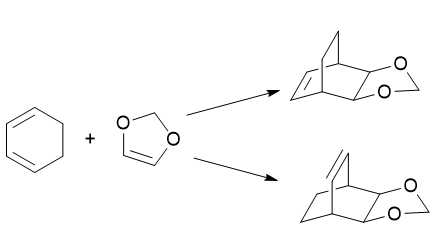
The reaction carried out was a Diels-Alder cycloaddition between cyclohexadiene and 1,3-dioxole. Two possible reaction pathways were investigated, involving an exo and endo approach of the reactants. All calculations were initially performed at the PM6 level to act as a guide for subsequent calculations at the B3LYP level. IRC calculations were carried out at the PM6 level only due to time constraints.

MO Diagram

(Fv611 (talk) There is not much point in presenting two MO diagrams (endo and exo) if you draw them in the same way and do not mention at all the difference between endo and exo conformation in terms of relative MO energies)

Reactant MOs
Cyclohexadiene HOMO	Cyclohexadiene LUMO	1,3-Dioxole HOMO	1,3-Dioxole LUMO

Endo MO Diagram	Exo MO Diagram

Transition State MOs
Endo HOMO -1	Endo HOMO	Endo LUMO	Endo LUMO +1
Exo HOMO -1	Exo HOMO	Exo LUMO	Exo LUMO +1

As before, the MO diagrams show that only orbitals of the same symmetry interact to form transition state MOs which are higher in energy than the reactants. By looking at the calculated energies of the orbitals as seen on the JMol applets, we can see that for the combination of reactants, the HOMO of the system will be on the 1,3-dioxole at -0.19591 Hartrees, while the LUMO will be on the cyclohexadiene at -0.01709 Hartrees. Since the HOMO is located on the dienophile and not on the diene as is usually the case, the reaction is defined as having inverse electron demand. This is due to the presence of the electron-rich oxygen atoms instead of the usual electron-withdrawing substituents on the dienophile, raising the energies of the molecular orbitals.

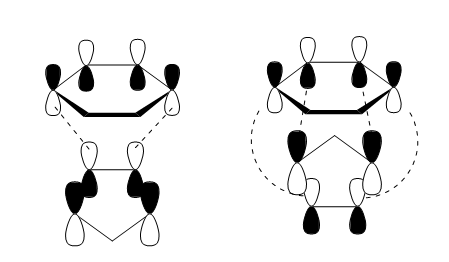
A comparison of the energies of the TS MOs for the exo and endo products shows that the endo HOMO has a lower energy than the exo HOMO, and the endo LUMO has a higher energy than the exo LUMO. When looking at the HOMO-1 and LUMO+1 the opposite holds true. This demonstrates that in the endo state, there is a greater overlap and stabilisation associated with symmetric MOs, and in the exo state there is greater overlap and stabilisation associated with the antisymmetric MOs. This could be an indication of the secondary orbital interactions possible for the symmetric orbitals in the endo form, as illustrated in Figure 9 below.

Nf710 (talk) 09:19, 6 March 2018 (UTC) So here you have compared the energies of the MOs in different potential windows thats means that the relative zeros will be different and therefore it doesn't make much sense to compare them. (This is due to how the potential and XC terms change with different number of atoms, it is not consistent if they have different numbers of atoms). You have come to the correct conclusion however.

Thermochemistry

Figure 8: Energy level diagram for both reaction pathways

Figure 9: Illustration of secondary orbital interactions in the endo form

Figure 10: Illustration of steric hinderance in the exo form

Geometry	Reactant Energies (kJ/mol)	TS Energies (kJ/mol)	Product Energies (kJ/mol)
Endo	-1313781.371	-1313621.557	-1313848.773
Exo	-1313781.371	-1313613.717	-1313845.155
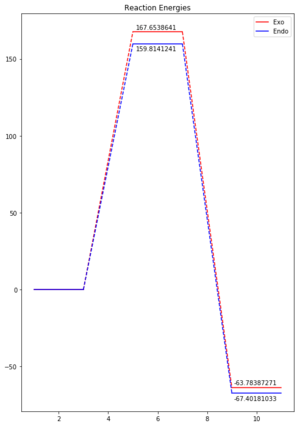
Relative Endo	0	159.814	-67.402
Relative Exo	0	167.654	-63.784

The reaction energies were taken from the B3LYP optimisation log files and converted into kJ/mol by multiplying by a factor of 2625.499. These have been plotted as shown in Figure 8. We can see that while the endo form of the product has a lower energy for both the activation barrier and the reaction energy, the difference reduces in size as we go from the transition state to the product. This suggests the factors involved in stabilising the endo form or destabilising the exo form have the greatest impact on the actual reaction pathway. It also shows that the endo product is both kinetically and thermodynamically more favourable.

The difference in energies could be due to two factors. One could be the previously mentioned stabilising secondary orbital interaction that occurs in the endo form. A look at the orbital lobes in the JMol file for the endo TS HOMO shows a clear interaction between the oxygen atoms on the 1,3-dioxole and the carbon atoms of the cyclohexadiene, which is not present in the exo form. The difference in energies could also be due to the slight steric clash present in the exo form - the hydrogen atoms on the sp3 hybridised carbons of the cyclohexadiene point toward the hydrogens from the sp3 hybridised carbon of the 1,3-dioxole. This could hinder the approach of the two molecules, and raise the reaction barrier.

Nf710 (talk) 09:21, 6 March 2018 (UTC) Good section, You have the correct energies. Your diagram of steric clashing is drawn in the wrong orientation and therefore is not shown them. But your SOO diagram is nice. There were a few parts where you could have gone into more detail.

Additional LOG Files

File:Mpg15 PROD OPT B3LYP endo.LOG

File:Mpg15 PROD OPT B3LYP exo.LOG

Exercise 3: Diels-Alder vs Cheletropic

Figure 11: Possible reactions of o-xylene and SO₂

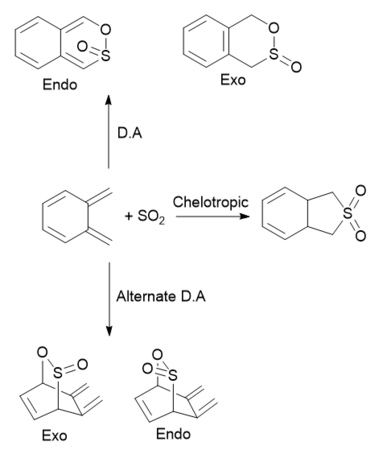
Multiple reactions of o-xylene and SO₂ were carried out. Two Diels-Alder cycloadditions and a chelotropic cycloaddition were carried out at the diene component formed outside of the o-xylene ring, and an additional pair of Diels-Alder cycloadditions were carried out on the diene fragment within the o-xylene ring. All calculations were carried out at the PM6 level.

IRC

Diels-Alder

Endo DA Animation	Endo IRC Plot

Exo DA Animation	Exo IRC Plot

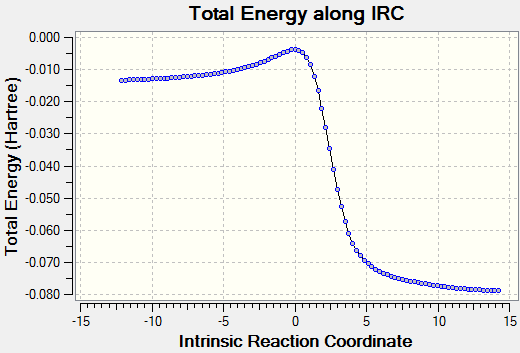
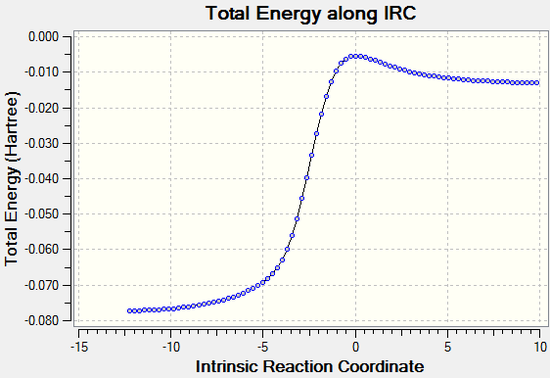
The IRC's for the first set of DA reactions show that in both cases the formation of C-O bonds occurs before the formation of C-S bonds, which can be explained due to the higher strength of C-O bonds (358 kJ/mol vs 259 kJ/mol). We can also see that the formation of an aromatic ring system occurs before any bonds are formed between the reactants, which is indicative of the instability of o-xylene.

Chelotropic

Chelotropic DA Animation	Chelotropic IRC Plot

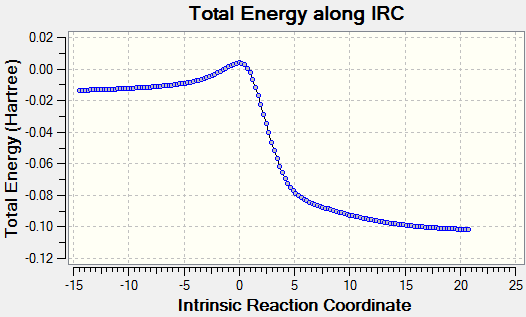
The IRC for this reaction once again shows the formation of the aromatic ring before the forming of any C-S bonds, which is likely driven by the twisting and bending of the terminal carbon atoms as the SO₂ molecule approaches. While not clearly visible due to the angle of the IRC animation, the formation of both C-S bonds is synchronous, as expected of a symmetric system.

Alternate Diels-Alder

Alternate Endo DA Animation	Alternate Endo IRC Plot

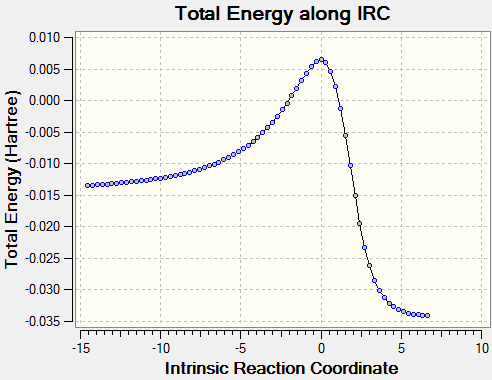
Alternate Exo DA Animation	Alternate Exo IRC Plot

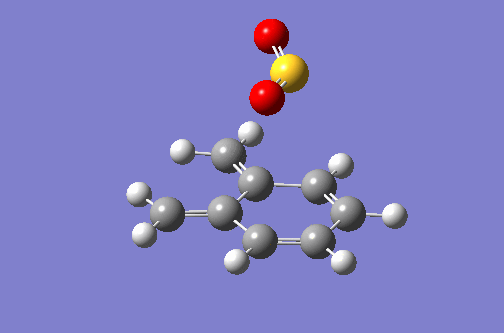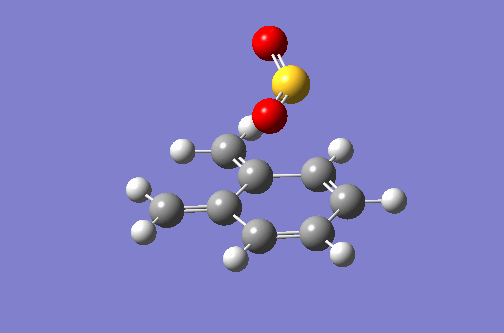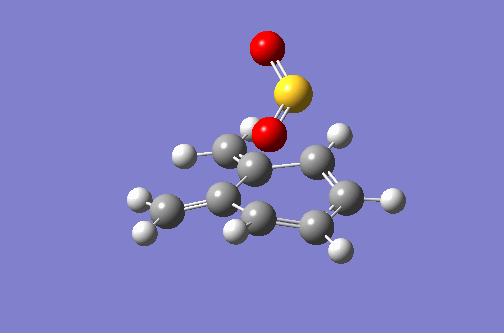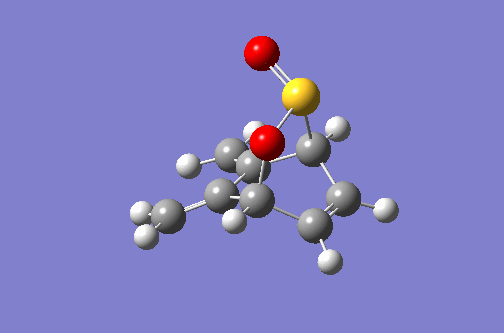
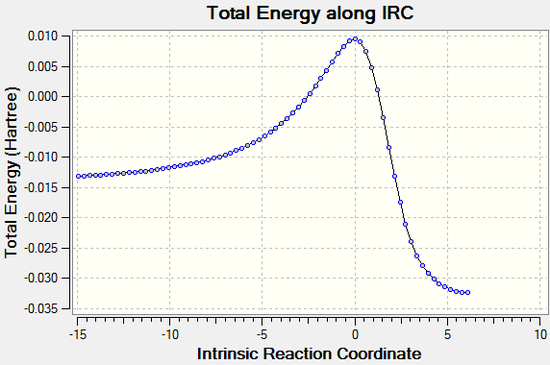
For the DA reaction at the alternate site, the IRC is very similar to the reaction above. The formation of C-O bonds again occurs before the formation of C-S bonds. In this case the formation of the aromatic system cannot occur.

Thermochemistry

Figure 12: Reaction Energies for the addition of o-Xylene and SO2

Reaction	Relative TS energy	Relative Product energy
Endo DA	84.187	-96.616
Exo DA	88.159	-97.262
Chelotropic	106.495	-153.597
Alternate Endo DA	114.393	18.667
Alternate Exo DA	122.230	23.115

A plot of all of the reaction energies and activation barriers shows the large differences between the different reactions carried out. The endo Diels-Alder cycloaddition at the first site has the smallest activation energy, making it the kinetically most favourable reaction. The difference in activation energies between the endo and exo forms is quite small, and the difference in product energies is essentially negligible, with the exo product being slightly lower in energy. The increased stabilisation in the endo transition state is likely due to the possibility of secondary orbital interactions much like in Exercise 2. The chelotropic reaction pathway has a higher activation energy than the DA reaction, but forms a much more stable product. This could be due to the fact both strong S=O bonds (522 kJ/mol) are kept intact during the reaction.

The DA reactions at the alternate site are by far the most unfavourable, with very large activation energies. Once again, the endo TS has a lower energy than the exo, which again suggests the presence of secondary orbital interactions. Overall the reactions are endothermic, with the products having a higher energy than the reactants, and the endo pathway being slightly lower in energy than the exo. This makes the reactions at this site both kinetically and thermodynamically unfavourable.

Additional LOG Files

Reactants:

File:Mpg15 REACT OPT SO2.LOG

File:Mpg15 REACT OPT RING.LOG

DA Cycloaddition:

File:Mpg15 EXO TS IRC.LOG

File:Mpg15 EXO TS CALC.LOG

File:Mpg15 EXO IRC PROD OPT.LOG

File:Mpg15 ENDO TS IRC.LOG

File:Mpg15 ENDO TS CALC.LOG

File:Mpg15 ENDO IRC PROD OPT.LOG

Chelotropic Cycloaddition:

File:Mpg15 CHELO TS IRC.LOG

File:Mpg15 CHELO TS CALC.LOG

File:Mpg15 CHELO IRC PROD OPT.LOG

Alternate DA Cycloaddition:

File:Mpg15 ALT EXO TS IRC.LOG

File:Mpg15 ALT EXO TS CALC.LOG

File:Mpg15 ALT EXO IRC PRODS OPT.LOG

File:Mpg15 ALT ENDO TS IRC.LOG

File:Mpg15 ALT ENDO TS CALC.LOG

File:Mpg15 ALT ENDO IRC PRODS OPT.LOG

Extension

Figure 13: Formation of cis and trans 2,3-dimethylaziridine

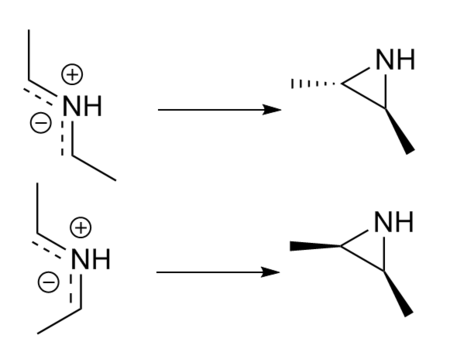
The reaction chosen for the extension was the electrocyclic formation of a 2,3-dimethylaziridine ring from a ylid linear form. Two different reactions were studied, differentiated by the stereochemistry of the reactant and product. All calculations were carried out at the PM6 level.

MOs

Trans reactant	Cis Transition state	Cis 2,3-dimethylaziridine
Reactant HOMO	TS HOMO	Product HOMO
Reactant LUMO	TS LUMO	Product LUMO

Cis amine reactant	Trans Transition state	Trans 2,3-dimethylaziridine
Reactant HOMO	TS HOMO	Product HOMO
Reactant LUMO	TS LUMO	Product LUMO

IRC's

Trans 2,3-dimethylaziridine DA Animation	Trans 2,3-dimethylaziridine IRC Plot

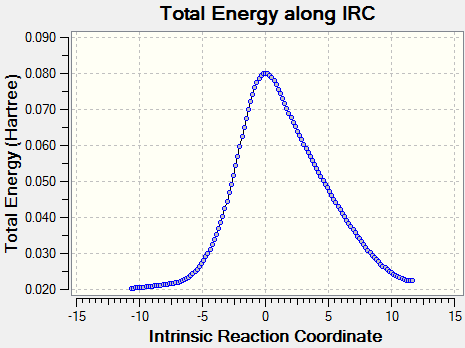
Cis 2,3-dimethylaziridine DA Animation	Cis 2,3-dimethylaziridine IRC Plot

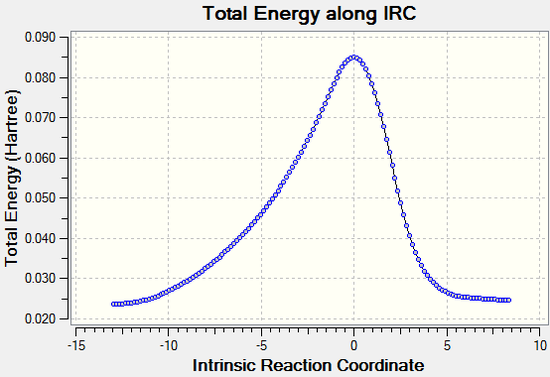
Discussion

Figure 14: Reaction energies for the formation of 2,3-dimethylaziridine

Figure 15: Diagram illustrating the conrotatory mechanism

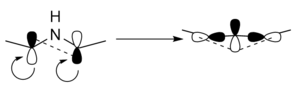
For the reaction in question, a Woodward-Hoffman analysis can be carried out to identify the reaction mechanism and to confirm if the reaction is thermally allowed. This is done with the use of the equation: $(4Q+2)s+(4R)a$, where s represents the number of suprafacial bond formations, and a represents the number of antrafacial bond formations. If the numbers of electrons involved that satisfy the equations for any given value of Q or S, and result in an odd sum, the reaction is thermally allowed. Otherwise, it is thermally disallowed.

In the case of this reaction, the bond formed is antrafacial, and involves a 4 electron system, as illustrated in Figure 15. This means the reaction is thermally allowed, and follows a conrotatory mechanism. The IRC's for both reaction pathways demonstrate the conrotatory nature of the reaction mechanism. This can also be seen by analysing the MOs of the reactant, TS and product. The TS shows a twisted geometry which has a bonding interaction between the two lobes of the p orbitals on the C atoms. In the product, a further interaction is seen with the p orbital on the nitrogen, due to the fact it is angled 'into' the three membered ring.

Geometry	Relative TS Energy	Relative Product Energy
Cis Ring	151.121	2.612
Trans Ring	144.888	1.940

A look at the reaction energies shows a fair difference in the activation energies. This is likely due to the greater steric clash that occurs during the formation of the cis ring. There is only a small difference between the two products, with the trans ring being slightly lower in energy. Overall the reaction is thermodynamically unfavourable, likely due to the strain present in the three membered ring.

(A very nice exercise, and a comparison between the two reactions. For the thermodynamics, you would probably need a better level of theory (B3LYP or better) to confirm Tam10 (talk) 15:04, 5 March 2018 (UTC))

Conclusion

The reactions of Butadiene and Ethylene, Cyclohexane and 1,3-Dioxole, o-xylene and SO₂ and the formation of a 2,3-dimethylaziridine ring were studied using computational methods. In most cases, calculations were carried out using the semi-empirical PM6 method, which offered reasonably accurate results whilst saving on computational time. Optimised structures for products, reactants and transition states were obtained, and these were used to generate MO diagrams and energy pathways for the reactions following an analysis of the relevant molecular orbitals. The reaction pathways were animated with the use of IRC calculations. Higher accuracy DFT calculations were used in the reaction of cyclohexane and 1,3-dioxole, which was studied using the B3LYP method. The increased accuracy of the method was shown in the MO diagrams that were generated in the reaction, which did not have any obviously missing orbital fragments, as was sometimes the case in the PM6 calculations. However, the close match between the calculated bond lengths in Excercise 1 and those found in the literature showed that even with its limitations, the PM6 method can offer fairly reliable results.

Overall, the methods used in this exercise showed that simulations of chemical reactions can offer a wide range of knowledge regarding the reaction pathway and its mechanism. The issue of the trade-off between accuracy and computational time was not very significant given the relatively simple reactions studied, but it can be seen that accurate simulations of complex chemical reactions can be very time consuming and costly to carry out.