Rep:Module 3:mh108 3apr9tru

The Coup Rearrangement

It is generally accepted that the Coup Rearrangement of 1,5-Hexadiene proceeds in a concerted fashion via either "chair" or "boat" like transition states. The aim was to simulate 1,5-Hexadiene using Gausview03 and calculate the relative energies of the two transition states and compare them to the lowest energy conformer of 1,5-Hexadiene using Gaussian to obtain the activation energy for the Coup Rearrangement. Furthermore different methods of transition state optimisation were considered for comparison of the method efficacy.

Optimizing the reactants and products

Method

With the aim to find the lowest energy conformation approximate anti and gauche-conformations of 1,5-hexadiene were cleaned and optimised by Gaussian03W with HF/3-21G method and basis set. To ensure accuracy further optimisation by Gaussian03W using B3LYP/6-31G were performed and the lowest energy anti-conformer was subjected to frequency analysis. The thermochemistry data were noted for comparison with the transition states energies. Other possible conformations were tested but are not reported here as the resulting relative energies were significantly higher for further details on these consult supplementary data files.

Results

HF/3-21G method and basis set revealed one of the possible gauche conformations most energetically stable, shown left, where the anti conformer, shown right, was disfavoured by 0.08kcal/mol. However with increased accuracy to B3LYP/6-31G the reverse was found to be true, where the anti conformer was favoured by 0.21kcal/mol. The calculation summaries with point group symmetries can be found in table 1 and 2.

Table 1	Anti-conformation 1,5-Hexadiene
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G
Charge	0
Spin	Singlet
E(RB3LYP)	-234.55969576 a.u.
RMS Gradient Norm	0.00004441 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group	CI

Table 2	Gauche-conformation 1,5-Hexadiene
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G
Charge	0
Spin	Singlet
E(RB3LYP)	-234.55933663 a.u.
RMS Gradient Norm	0.00000628 a.u.
Imaginary Freq
Dipole Moment	0.4198 Debye
Point Group	C1

The frequency analysis of the anti-conformer of 1,5-Hexadiene did not reveal any negative frequencies. For further details consult the supplementary material . The thermochemistry data is shown bellow. Note that the data is presented as calculated by Gaussian03W in Hartree with approximate accuracy ±3E-3a.u.

Sum of electronic and zero-point Energies           -234.416268
Sum of electronic and thermal Energies              -234.408957
Sum of electronic and thermal Enthalpies            -234.408013
Sum of electronic and thermal Free Energies         -234.447950

Discussion

The anti-conformer was expected to be more stable as for small molecules non-bonding interactions are small and unlikely to overcome destabilisation induced by the gauche conformation. Furthermore the resulting relative energy difference was within calculation error ≈2.4kcal/mol for the method and basis set used thus the use of more accurate method and basis set were required. The result confirmed expectations however is still within calculation error. In conclusion it can be assumed that the two conformations inter-convert freely at room temperature and our choice of anti-conformer for further comparison is purely arbitrary.

Optimizing the "Chair" and "Boat" Transition Structures

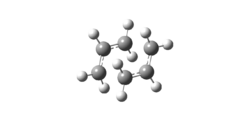
Method

A CH2CHCH2 fragment was optimised by Gaussian at HF/3-21G level and two copies were placed in approximate 'chair' transition state with ≈2.2A intermolecular distance, where the new and old bond would be in the Coup Rearrangement. Finally two different methods were used for optimisation of the approximate transition state.

In the first method force constants were calculated followed by an optimisation of the Hessian matrix, opt + freq with optimisation to a TS (Berny), with additional, opt=noeigen, to prevent crashing of the Gaussian calculation if the guess was not accurate enough. In the second method the reaction coordinates were frozen and the rest of the molecule optimised, mod=redundant. After optimisation the reaction coordinates were unfrozen and TS optimised as before but without the force constant calculation. Both methods used HF/3-21G level optimisation.

The 'boat' transition state was reached and optimised by QST2 at HF/3-21G level by specifying the reactant and product as the same 1,5-hexadiene with complementary atom numbering. However this method fails if the conformation is not adjusted with reacting bonds in the right orientation thus the dihedral angle of the four middle carbon atoms was changed to 0° with each C-C-C bond angle of 100° as shown.

To make calculation of the activation energy and comparison with the ground state configuration possible both transition states were further optimised at B3LYP/6-31G level and subjected to IRC in order to find which conformer is originally formed during the Coup Rearrangement from lower energy 'chair' transition state. The number of steps used for IRC was 50 after that the structure was optimised using HF/3-21G level to reach minimum energy.

Results

Table 3	Chair TS Optimisation
File Type	.log
Calculation Type	FTS
Calculation Method	RB3LYP
Basis Set	6-31G
Charge	0
Spin	Singlet
E(RB3LYP)	-234.50546727 a.u.
RMS Gradient Norm	0.00003546 a.u.
Dipole Moment	0.0002 Debye
Point Group	C1

Table 4	Boat TS Optimisation
File Type	.log
Calculation Type	FTS
Calculation Method	RB3LYP
Basis Set	6-31G
Charge	0
Spin	Singlet
E(RB3LYP)	-234.49291456 a.u.
RMS Gradient Norm	0.00001063 a.u.
Dipole Moment	0.0704 Debye
Point Group	C2V

Both methods for the calculation of the 'chair' transition state showed one imaginary frequency at 818cm-1 at HF/3-21G level. However for accurate comparison the B3LYP/6-31G level was necessary, which revealed the imaginary frequency at 562cm-1 and thermochemistry data as shown below. Note again that the data are presented as calculated by Gaussian03W in Hartree with approximate accuracy ±3E-3a.u. to allow accurate comparison.

Thermochemistry data for Chair Transition state
Sum of electronic and zero-point Energies=           -234.362665
Sum of electronic and thermal Energies=              -234.356753
Sum of electronic and thermal Enthalpies=            -234.355809
Sum of electronic and thermal Free Energies=         -234.391591

The activation energy of this process at 0K is 33.6kcal/mol and 32.8kcal/mol 298.15K. Finally following the reaction by IRC and optimising the structure resulted in a gauche structure with relative energy of -1.45E5 kcal/mol and C2 symmetry.

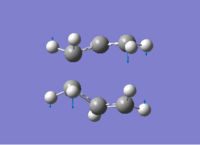
The boat structure optimised at HF/3-21G level has one imaginary frequency at 840cm-1. Again after further optimisation at B3LYP/6-31G level -505cm-1 with thermochemistry data as shown below again presented in Hartree with approximate accuracy ±3E-3a.u. Both transition states can be view in Jmol above and optimisation summaries are availible in table 3 and 4.

Thermochemistry date for Boat Transition state
Sum of electronic and zero-point Energies=           -234.351356
Sum of electronic and thermal Energies=              -234.345053
Sum of electronic and thermal Enthalpies=            -234.344109
Sum of electronic and thermal Free Energies=         -234.380121 

The activation energy for the Coup Rearrangement via a boat transition state at 0K is 40.7kcal/mol and 40.1kcal/mol at 298.15K. The activation energies can be found in table 5, vibrations are shown below.

Table 5	B3LYP/6-31G	B3LYP/6-31G	Experimental
	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	33.6	32.8	33.5 ± 0.5
ΔE (Boat)	40.7	40.1	44.7 ± 2.0

Chair TS

Boat TS

Disscusion

The most striking difference is in the value calculated for the imaginary frequencies of the transition states for the two levels of calculation employed, HF/3-31G and B3LYP/6-31G. However it should be noted that the quantities are not comparable as the vibrations are not real and cannot be measured. Importantly they both represent the same vibration that resembles the Coup Rearrangement and do not show any other imaginary frequency confirming the structure as a transition state of the Coup Rearrangement. Finally the value for the activation energy is comparable to measured quantity, when higher level calculation is used.

Conclusion

Transition state structure can be obtained via numerous methods however each method has its advantages and disadvantages, for example the QST2 is fully automated however does not consider rotation of bonds and fails to provide an answer if the right conformation is not used; optimisation with use of force constants is fastest but needs an accurate prediction of the transition state; finally the use of Hessian matrix is the most reliable but for small molecules like this one too complex and a relatively good prediction of the transition state is still needed.

However all the methods provided in the end a valid answer with comparable results to the experiment and can all find its use in the calculation of transition states depending on the complexity of the molecule and if the approximate structure of the transtion state is known or not.

The Diels Alder Cycloaddition

The aim was to analyse the relative energy of the transition state in the Diels Alder reaction and rationalise the selectivity based on calculated molecular orbitals and transition state structures.

Molecular Orbitals of butadiene

The aim was to calculate and assign symmetry to butadiene HOMO and LUMO in order to understand the possible interaction in Diels Alder cycloaddition and finally use them later for comparison with the HOMO of the transition state in Diels Alder reaction.

Method

Butadiene was simulated by Gaussview03 and optimised at B3LYP/6-31G level by Gaussian03W. The molecular orbitals were then calculated at the same level of calculation to ensure accuracy. Finally the MO symmetry was assigned for further comparison with the Diels Alder Cycloaddition transtion state.

Result

Table 6	cis-Butadiene OPT
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G
E(RB3LYP)	-155.95382512 a.u.
RMS Gradient Norm	0.00001691 a.u.
Dipole Moment	0.0941 Debye
Point Group	C2V

The optimisation summary can be viewed in table 6 on the right. The important result of this calculation are the symmetries of highest occupied and lowest unoccupied molecular orbitals (HOMO and LUMO). The HOMO is a bonding orbital, which is antisymmetric with respect to xz and yz plane and symmetrical with respect to xy plane. The LUMO is still a bonding orbital, although it is on the border line and can be considered non-bonding. It is symmetrical with respect to xy and xz planes but anti-symmetrical with respect to yz plane.

HOMO

LUMO

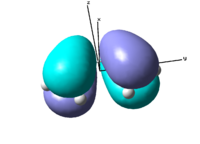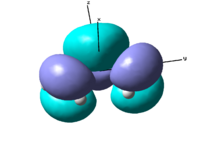Discussion

Ethene the dienophile in the Diels Alder Cycloaddition under consideration approaches butadiene from front of the top or bottom face, parallel to xy and yz plane, where the HOMO-LUMO interactions can occur, thus the symmetry with respect to these planes are not relevant. However the perpendicular interaction with respect to xz plane stresses the importance of MO reflectional symmetry with respect to this plane.

In conclusion, even though both HOMO and LUMO of butadiene are symmetrical and antisymmetrical depending on the plane under consideration, it is only the symmetry with respect to xz plane that is relevant thus the HOMO is anti-symmetrical and LUMO symmetrical. Furthermore the HOMO and LUMO of ethene have complementary symmetry with respect to the xz plane allowing for interactions.

Prototype Transition State in Diels Alder Cycloaddition

The aim was to get insight into the molecular orbital interaction and geometry in Diels Alder transition state (TS) and identify the molecular orbitals participating in the reaction between butadiene and ethene.

Method

Table 7	Diels Alder TS
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G
Charge	0
Spin	Singlet
E(RB3LYP)	-234.49456035 a.u.
RMS Gradient Norm	0.00002031 a.u.
Imaginary Freq	1
Dipole Moment	0.4506 Debye
Point Group	C1

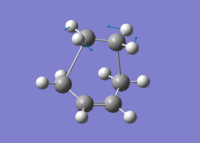
Assuming envelope like structure of the transition state in Diels Alder Cycloaddition of butadiene with ethene as shown in fig. 1, where the butadiene fragment and ethene fragment were frozen 2.14A apart and optimised using Mod-redundant at HF/3-31G level using Gaussian03W. After the optimisation the bonds were unfrozen and derivated to reach a transition state at the same level of theory. Finally the pre-optimised transition structure was optimised at B3LYP/6-31G level and molecular orbitals computed at the same level of theory.

Results

The transition state was shown to have an envelope like structure with a bond angle of 102.2°±0.1 between the former ethene fragment and butadiene fragment. The newly forming C-C σ bonds have bond length of 2.26A and an imaginary frequency of -534cm-1. The transition structure can be seen in Jmol in fig.1 with the optimisation summary in table 7.

The imaginary vibration is a synchronous stretching/compressing vibration corresponding to the concerted formation of the two new C-C σ bonds. On the other hand the first real vibration is a an asynchronous bending vibration corresponding to twisting of the ethene fragment with respect to the reaction plane.

Imaginary Frequency

First Real Frequency

Ethene HOMO

Ethene LUMO

TS HOMO

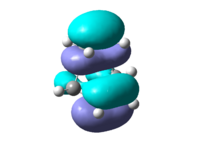
The HOMO and LUMO of ethene are shown for illustration of the MOs participating in the reaction. The HOMO is a symmetrical orbital and the LUMO antisymmetrical with respect to the xz plane. Finally the resulting HOMO of the transition state is symmetrical MOs.

Discussion

The sp3, sp2 bond lengths for carbon are 1.53A and 1.34A respectively both much shorter than the two forming σ C-C bonds in the transition state. However the newly forming bonds are shorter than the sum of Van der Waals radii of two carbon atoms, 3.40A.Furthermore the bond lengths of the original C=C in the starting material have prolonged to 1.39A and the single bond contracted to 1.41A indicating shifting of the electron density in the transition state compared to the starting material. It can be concluded that the structure shown is indeed a transition state, where sp2 bonds are broken and new sp3 bonds formed in a concerted fashion as similar bonds have similar lengths.

Similar conclusion can be made from the MO mixing. The HOMO of ethene is mixing with the LUMO of butadiene resulting in an orbital with even electronic distribution in the transition state i.e comparable bond lengths for originaly similar bonds. The mixing, and thus the reaction is allowed, due to similar molecular orbital symmetry. If the symmetry waas opposite the reaction could not proceed due to selection rules.

Relative Energies of Exo and Endo TS in Diels Alder Reaction

Assuming that the major product of Diels Alder Cycloaddition is kinetically controlled; the aim was to calculate the relative energies of exo and endo transition states in Diels Alder Cycloaddition in order to support the assumption and rationalise the observed selectivity.

Method

The relative energies of exo and endo transition states were simulated on the reaction of cyclohexa-1,3-diene reaction with maleic anhydride. The transition states were calculated as before by Mod-redundant starting from previously calculated distances between the diene and dienophile in the Diels Alder transition state and optimized at HF/3-31G level followed by B3LYP/6-31G. Finally the molecular orbitals were computed at the same level of theory by Gaussian.

Results

Table 8	Endo TS
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G
Charge	0
Spin	Singlet
E(RB3LYP)	-612.49547769 a.u.
RMS Gradient Norm	0.00000668 a.u.
Imaginary Freq	1
Dipole Moment	7.0088 Debye
Point Group	C1

Table 9	Exo TS
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G
Charge	0
Spin	Singlet
E(RB3LYP)	-612.49098153 a.u.
RMS Gradient Norm	0.00000657 a.u.
Imaginary Freq	1
Dipole Moment	6.3940 Debye
Point Group	C1

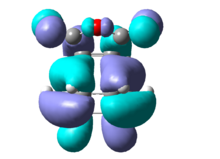
Both in the endo and exo transition states the maleic anhydride approaches from top face however in the endo transition state the -(C=O)O(C=O)- component of maleic anhydride is directly above the newly forming double bond whereas in the exo TS it is opposite to it resulting in different MO interactions with a different energy HOMO and consequent different relative energy of the transition state. The endo transition state has a relative energy of -3.84342E5kcal/mol with an associated imaginary frequency at -447cm-1 corresponding to the Diels Alder addition as discussed above. The exo transition state has a relative energy of -3.84339E5kcal/mol, 2.82kcal/mol less stable than the endo TS, and has an associated imaginary frequency of 448cm-1. Summary of the optimisation and frequency calculation parameters are in table 7 and 8.

Endo HOMO view 1

Endo HOMO view 2

Exo HOMO view 1

Exo HOMO view 2

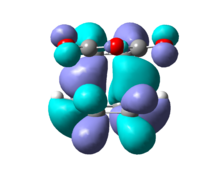The atomic orbital interaction in the HOMO between -(C=O)O(C=O)- and the rest of the molecule have one extra nodal plane in the exo TS compared to the endo TS. The nodal plane is located between the central oxygen atom and the C-C antibonding component of the MO on cyclohexa-1,3-diene. Whereas similar interaction with the double bond on the other side of the molecule is favoured due to complementary symmetry.

Discussion

The energy difference between the two transition states supports the assumption that the kinetic endo product is formed. The energy difference calculated is small as it is only the outcome of secondary orbital overlap, where the exo TS have one extra nodal plane with a distant part of the molecule, however large enough to drive the reaction selectively to the endo product. On the other hand if the cyclohexa-1,3-diene was substituted this negative interaction might be replaced resulting in different selectivity. In conclusion the selectivity is highly dependent on the nature of the subsituents on the diene and the dienophile.

Conclusion

In conclusion it is the HOMO of ethene that interacts with LUMO of butadiene however similarly the LUMO of ethene can interact with HOMO of the butadiene as it is also allowed by symmetry. The interaction only depends on further substituents on the diene and the dienophile, which can shift the electronics of the reaction but in either case the reaction will proceed in a concerted fashion forming both new bonds simultaneously while redistributing the electronic density around the newly formed molecule.

Furthermore the endo selectivity observed is a produt of kinetic reactivity, where the endo transition state has lower energy but it is also highly dependable on the substitent groups that can shift the electronic distribution negating the unfavourable interactions and possibly reversing the selectivity to exo product.

Finally large substituens on both the diene and the dienophile can prevent formation of one of the transition states by hindering the access from the most favourable angle. If this happens the electronic attractions that predominate in the unsubstituted reactants might be overcome by new negative interactions between substituent groups.

In conclusion selectivity and reactivity in the Diels Alder cycloaddition is substrate specific and cannot be generalised from two simple examples as discussed here. For reactivity and selection of further substituted reactants in Diels Alder reaction visit.