Rep:Module3rh1909

Module 3

The Cope Rearrangement

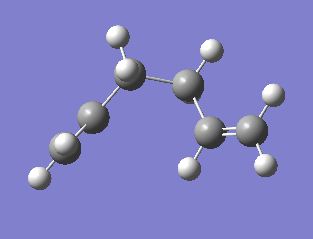
This part of the module will study the [3,3]-sigmatropic shift seen in the Cope rearrangement of 1,5-hexadiene. The reaction scheme is shown below.

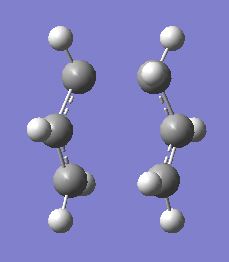
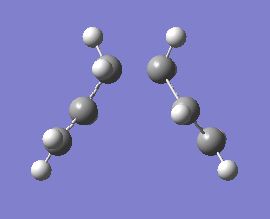
Firstly, an anti- and a gauche- conformer of 1,5-hexadiene will be optimised using the HF/3-21G level of theory. A prediction of the lowest energy conformer is then optimised and their structures compared to those given in APPENDIX 1 of the module. Below is a table showing the results of the optimisations, with energies and point groups of each conformer. See links here for .chk files. Media:Reaction_anti2_rh.chk, Media:Reaction_gauche_rh.chk and Media:Reaction_gauche_hypothesis_lowest_conformer.chk

Conformer	Total Energy (Hartrees)	Point Group
anti2	-231.69254	Ci
gauche5	-231.68962	C1
gauche3	-231.69266	C1

As you can see, the values for the total energy of these conformers are in very strong agreement with the values given in APPENDIX 1, in fact, they are exactly the same!

The anti2 conformer was then optimised using the B3LYP/6-31G* level, a higher level of theory than HF/3-21G. Media:Reaction_anti2_DFT.chk. A successful frequency analysis of the structure was also carried at this level. Media:Reaction_anti2_DFT_freq.chk. The angles and dihedral angles, and total energies for both optimised structures were then compared. See table below.

	HF/3-21G	B3LYP/6-31G*
	Angle (Deg)	Angle (Deg)
H-C2-C3-H	174.28	176.89
H-C3-C4-H	180.00	180.00
C1-C2-C3	124.80	125.29
C2-C3-C4	111.34;	112.67
Total Energy (Hartree)	-231.69254;	-234.61170;

As you can see, the total energy for the B3LYP/6-31G* optimised structure is a considerably lower energy than the structure optimised to a lower level. Comparing the angles of the two structures shows that the higher level of theory has larger angles, bar the H-C3-C4-H angle, and although the increase in angle and change in overall geometry is small, it does have a stabilising effect on the conformer.

It is known that the Cope rearrangement can occur via a chair- or boat-like transition state. The chair transition state will be studied first and modelled using two C₃H₅ allyl fragments placed 2.2angstroms apart with C_2h symmetry. The fragments are optimised to a transition state and frequency analysed using the HF/3-21G level of theory. Media:Chair_ts_guess_opt_freq_-_Copy_-_Copy.chk. The optimised structure is shown in the picture.

The frequency analysis showed the presence of one imaginary (negative) frequency at -818cm^-1 as expected, and visualisation showed the vibration correctly corresponding to the Cope rearrangement. The terminal allyl carbons move towards and away from each other, with each end of the fragments moving in a non-concerted fashion.

The two allyl fragments were then optimised using the frozen coordinate method. See optimisation files here. Media:Chair_ts_guess_opt_second_method.chk and Media:Chair_ts_guess_opt_second_method_part2.chk. This gave an optimised transition state as shown in the picture.

The geometry after this optimisation is obviously quite different to the first optimisation. The distances between the terminal carbons are 1.55angstroms for one pair, and 4.39angstroms for the other. This suggests that the transition state is not symmetrical and is either more similar to the reactant or to the product. As this reaction is a concerted pericyclic reaction, an asymmetrical transition state is not feasible. This has been confirmed in previous studies.

The boat conformation was then studied. Originally, the QST2 method was used to optimise the two allyl fragments (now in a boat-like, C_2v position). This method failed a number of times, so it was abandoned, and the QST3 method was used. Media:BOAT_TS_GUESS_QST3.LOG.

These optimised transition states were then further optimised to a B3LYP/6-31G* level. See file here for chair optimisation Media:Chair_ts_b3lyp_opt_partg.chk and boat optimisation Media:Boat_ts_b3lyp_opt.chk. The energies from both levels of theories can be seen in the results table below, along with the energies of the resulting conformer of the product. The conformations of the products were calculated by carrying out an IRC on the transition states.

The chair transition state was run for 50 cycles but failed, the error message said that a minimum was not found within this number of cycles. The next step was to double the number of cycles to 100, however, the IRC still failed. Then the IRC was set to calculate force constants at each step of the process, this was successful. The product is clearly the gauche2 conformer, with a total energy of -231.69164 Hartree, in very close agreement with the values in APPENDIX 1. The final conformation is shown below.

An IRC was run for the boat transition state. A minimum was found after just 50 cycles, most probably because the more accurate QST3 method was used to find the transition state structure. The product is clearly the gauche3 conformer, with the lowest energy of -231.69266 Hartree.

The conformation is shown below.

The results table below shows all the energies of both transition states and of the reactants is shown below.

	HF/3-21G			B3LYP/6-31G*
	Electronic Energy (Hartree)	Sum of Electronic and Zero-Point Energies (Hartree)	Sum of Electronic and Thermal Energies (Hartree)	Electronic Energy (Hartree)	Sum of Electronic and Zero-Point Energies (Hartree)	Sum of Electronic and Thermal Energies (Hartree)
		At 0K	At 298.15K		At 0K	At 298.15K
Chair Transition State	-231.61932	-231.46670	-231.46134	-234.55698	-234.41493	-234.40901
Boat Transition State	-231.60280	-231.45093	-231.44530	-234.54309	-234.40234	-234.39601
Anti2 Reactant	-231.69253	-231.53954	-231.53257	-234.61170	-234.46921	-234.46186

The table below shows the activation energies.

	HF/3-21G		B3LYP/6-31G*		Experimental
	At 0K	At 298.15K	At 0K	At 298.15K
ΔE Chair (kcal/mol)	45.7	44.7	34.0	33.2	33.5
ΔE Boat (kcal/mol)	55.6	54.8	42.0	41.3	44.7

As you can see from the results tables above, the activation energies at 0K and 298.15K for the chair transition state are much lower than for the boat transition state. This is in accordance with many studies. It should also be pointed out that by optimising at the B3LYP/6-31G* level of theory, the activation energies are in very strong agreement with experimental values and are more accurate.

The results of the IRC also back up these results. The product formed via the boat transition state is the lowest energy conformer. This means that reaction via the boat transition state is the thermodynamic path, giving the most stable product. Likewise, the reaction via the chair transition state gives the second from last stable product, and reaction occurs via kinetic pathway.

</body>

</html>