Rep:Module3:yinweiwoaini
The Cope Rearrangement Tutorial
The Cope Rearrangement involves rearrangement of electrons in 1,5-dihexene via a 'chair' or 'boat' transition structure. Here we calculate the energy minimum of the transition structures to determine which is the prefered pathway. [1]
Optimizing the Reactants and Products
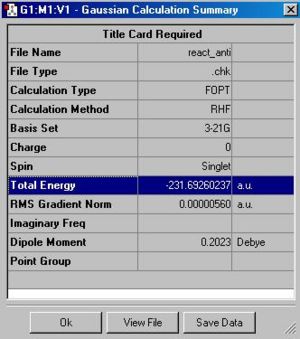 |
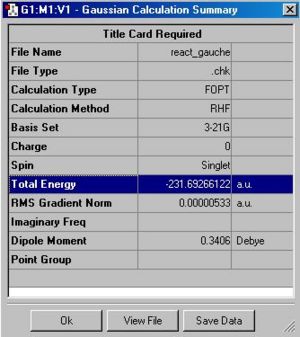 |
The final anti-structure has an energy of -231.69260 Hatrees and symmetry with point group: C2.
The final gauche-structure has an energy of -231.69266 Hatrees and symmetry with point group C1.
One would have expected the anti comformation to have the lowest energy. However computational chemistry shows that the gauche-structure infact has the lower energy.
Appendix 1 contains the low energy conformers of 1,5-hexadiene and their point groups. The structures I have generated are the gauche3 and anti1 conformers.
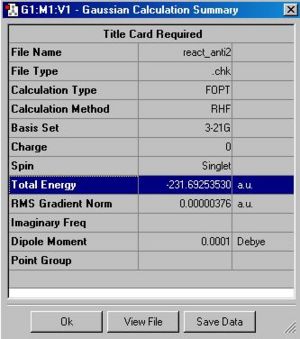
The final anti2-structure has an energy of -231.69254 Hatrees and symmetry with point group: Ci. This is the same as given in the appendix.
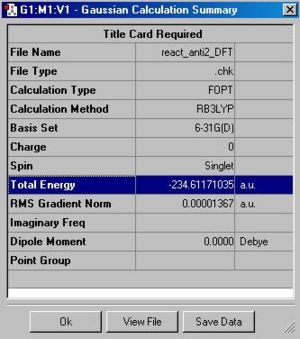
The final anti2-structure has an energy of -234.611710 Hatrees and symmetry with point group: Ci. This is different from the previous calculated energy and is assumed to be more accurate to the use of a higher theory.
The vibrations are positive and real and hence shows that the critical point is a minimum.
- Sum of electronic and zero-point Energies: -234.469204
- Sum of electronic and thermal Energies: -234.461857
- Sum of electronic and thermal Enthalpies: -234.460913
- Sum of electronic and thermal Free Energies: -234.500777
(Energies given in Hatrees)
Optimizing the "Chair" and "Boat" Transition Structures
The guide for the procedures for the optimisations can be found here.
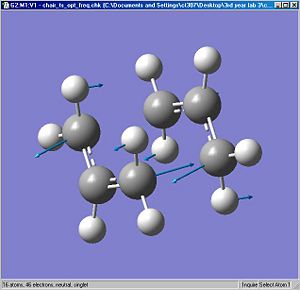
There is an imaginary vibration at -818 cm-1 .
Here a QST2 calculation is performed which uses the HF/3-21G basis set and minimum to TS (QST2). The job fails because the structure looks a bit like a dissociated chair transition structure. The calculation only translates the top allyl fragment and does not consider the possibility of a rotation around the central bonds. The reactant and product geometries to make it close to the boat geometry. The calculation is performed again, this time succesfully. Analysis of the frequency shows a negative vibration where the C1 and C6 atoms come together to form a bond , while the C3-C4 bond extends until the bond breaks.
 |
 |
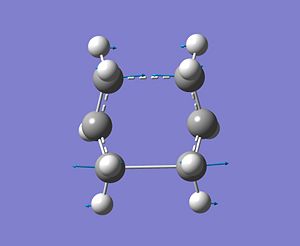
Next the optimised transition state was sent to IRC calculation. Since the reaction coordinate is symmetrical, it was computed it in the forward direction. The energy of the structure was calculated to be -231.69267 Hartree.
| HF/3-21G | HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | B3LYP/6-31G* | |
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| Chair TS | -231.61932 | -231.466701 | -231.46134 | -234.55698 | -234.41492 | -234.40899 |
| Boat TS | -231.60280 | -231.45093 | -231.445302 | -234.543092 | -234.40233 | -234.39601 |
| Reactant (anti2) | -231.69254 | -231.53954 | -231.53257 | -234.61171 | -234.46920 | -234.46185 |
The calculated values are almost exactly same as the values from the RESULTS TABLE. We can see that the chair transition state is more stable than the boat transition state, with the energy difference between the TS and product being 43 kJ/mol and 34kJ/mol. The chair TS would be the prefered transition state and pathway since this would be the lowest activation energy.
The Diels Alder Cycloaddition
The Hartree Fock and the 3-21G basis set have been used in this section unless otherwise stated. A guide to the procedures for optimisation can be found here.
Molecular Orbital
 |
 |
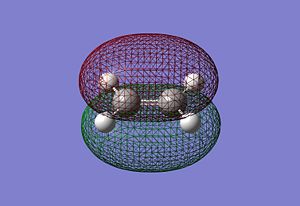 |
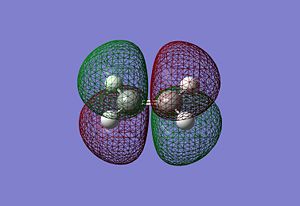 |
It can be seen that the HOMO of the cisbutadiene is unsymmetric with respect to the plane while the LUMO is symmetric. On the other hand the HOMO of the ethene is symmetric with respect to the plane while the LUMO is unsymmetric. One would expect the HOMO of the cisbutadiene react with the LUMO of the ethene, or the HOMO of the ethene to react with the LUMO of the cisbutadiene to form two new bonding MOs. Both reactions are allowed. The HOMO-LUMO have similar symmetry properties and so there is a significant overlap density for interaction.
Transition State
 |
 |
 |
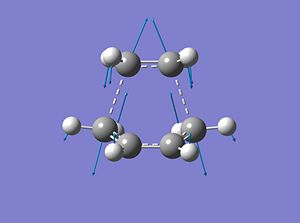
Although not clearly shown, the transition state molecular orbital of the cycloaddition suggests the HOMO of the cisbutadiene interacts with the LUMO of the ethane to form the product.
The interfragment C-C distance is 2.21Å which is much smaller than the σ C-C bond distance (1.54Å)[2]. This means it is not yet a bond, however, it is within the sum of the Van der Waals radius of carbon (3.4Å). This suggests that it exists as something between nothing (no interaction) and a bond, and is what we call a transition state.
There is an imaginary vibration at -818 cm-1 which corresponds to the interaction of the fragments during the cycloaddition. If the blue displacement arrows are reversed then it will show the terminal carbons of the cisbutadiene and the ethene converging towards each other. The vibration is symmetrical and so the formation of the two new bonds should be synchronous.
Regioselectivity
 |
 |
The endo product has an energy of -0.0515 Hartrees and the exo product has an energy of -0.504 Hartrees which means the endo product is thermodynamically favoured product. The maleic anhydride fragment is situated almost paralell and next to the cyclohexa-1,3-diene in the endo product, whereas in the exo product is is situated away from the diene. One would expect the endo product to be higher in energy and less favourable due to the steric clash between the diene fragments and the -(O=C)-O-(C=O)- fragment of the anhydride. However there exists a secondary orbital overlap between the two groups in the endo product which is not possible in the exo product. This overlap stabilises the product, and most importantly, the stabilisation overcomes the destabilisation from the steric clash.
