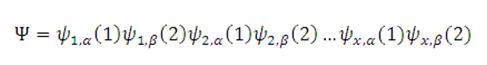Rep:Module3:tb407
Module 3: The Transition State
The Cope Rearrangement
Optimisation of reactants
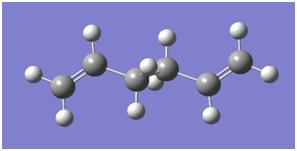
A molecule of anti - 1,5-hexadiene (fig. 1) was drawn using GaussView and optimised using a Hartree-Fock (HF) calculation method and a 3-21G basis set.
File:Anti 1,5 hexadiene tb407.jpg
The Hartree-Fock method treats the molecular wavefunction as a product of single electron wavefunctions[1].
In the above equation, the molecular orbital (Ψ) is written as a sum of atomic wavefunctions (ψ1...ψx), each containing two electrons (1 & 2) with spins α and β.
A prerequisite of the wavefunction is that if the spins of electrons 1 or 2 are reversed in a particular orbital (particle exchange), then the sign of the wavefunction must change. This occurs due to Pauli's principle, which states that if the "label" of two fermions (such as electrons) changes, the overall wavefunction must change sign[3]. In order to achieve this behaviour, the wavefunction must contain the other possible particle positions.
This can then be written as a Slater Determinant.
The variational principle is applied to this general wavefunction and the coefficients of each term weighted such that the lowest energy is given, when the wavefunction is put into the Schrodinger Equation.
The 3-21G basis set determines the atomic orbitals (ψ1, ψ2...ψx), which can be used in this method and Slater determinant. The method is not costly and gives results of comparable quality to those yielded by higher level basis sets such as 4-21G, 4-31G and STO-3G[6].
The product of the optimisation at this level is shown in fig. 2[7].
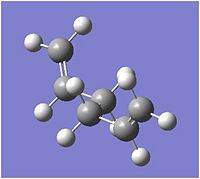
The energy of this optimised structure was calculated to be -231.69260 Hartree, in perfect agreement with the value in appendix 1 of the wiki. The structure was symmetrised and the point group calculated to be C2.
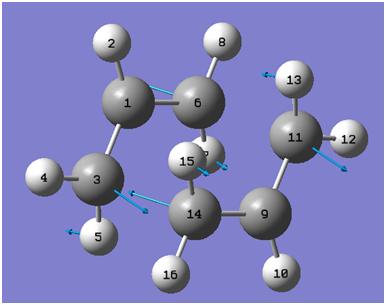
The energy of the gauche form (fig. 3) may be expected to be higher than that of the anti form of the 1,5-hexadiene, since it involves much more steric hindrance in the molecule due to the proximity of the two alkene groups to each other.
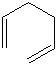
The product of optimisation at the same level as for the anti form is given in fig. 4[8][9].
File:Gauche C2 (1) optimised tb407.JPG
The energy of this molecule was calculated to be -231.68916 Hartree, once again in perfect agreement with the result in appendix 1 of the wiki. The structure was symmetrised and the point group found to be C1. The energy calculated was indeed less negative than that observed after optimising the anti structure, confirming that the prediction made that the gauche structure would be less stable was correct.
The lowest energy conformation of the molecule can be assumed to be an anti structure (as demonstrated above.) It may also follow that the lowest energy conformation maximises the distance between the two alkene double bonds in the structure (given the evidence from the higher energy of the gauche molecule with alkenes close to each other.
This proves to be the case. Upon changing the anti structure[10] so that the alkene bonds no longer point in the same direction (as they do in the C2 structure) the energy of the structure drops to -234.62318 Hartree (Ci point group.)
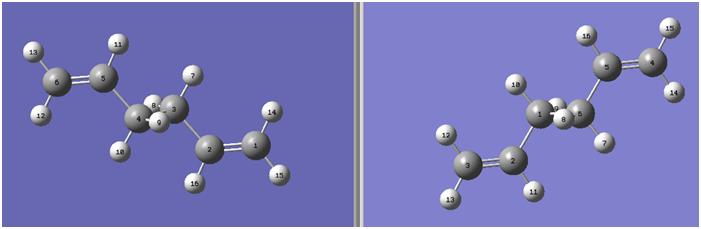
The HF/3-21G optimised Ci structure was further optimised using the DFT B3LYP method and the 6-31G* basis set[11], which are higher level approximations. The geometries of the two optimised structures are very similar. The C2-C3-C4 and C3-C4-C5 angles in the structure reoptimised at B3LYP/6-31G (right in the image below) is 112o. This is close to the value of 111o observed in the structure optimised by HF/3-21G (left.) The dihedral angle betwee C2 and C4 for the B3LYP/6-31G* structure is exactly 180o vs 179o for the HF/3-21G optimised structure. Thus the geometry of the optimised structure does not vary much with the method and basis set used.
On the other hand, the energies of the two different optimisations are quite different. The HF/3-21G optimised structure has energy -231.68916 Hartree cf. -234.62317 Hartree for the B3LYP/6-31G* optimised structure. Given that the B3LYP/6-31G* set-up is the higher level optimisation, it is reasonable to assume that this is probably the more accurate of the two energies.
In order to compare the energy of the molecule with experiment, a frequency prediction was carried out[12] on the B3LYP/6-31G* optimised structure at the same level. The reason that this must be carried out before comparisons with literature can be made is that the energy calculated in the optimisation does not contain any contributions from zero point energy or rotational/vibrational and translational energies at room temperature and therefore is not very accurate.
The vibrations calculated all returned with a positive frequency, which suggests that the calculation has succeeded. The predicted IR spectrum is given in fig. 5.
File:IR spec anti cope Ci tb407.JPG
The thermochemistry data obtained from the .log file is as follows.
Sum of electronic and zero-point Energies= -234.469199 Sum of electronic and thermal Energies= -234.461855 Sum of electronic and thermal Enthalpies= -234.460911 Sum of electronic and thermal Free Energies= -234.500776
The correction to the energy due to the zero point energy is calculated to be 0.142520 Hartree, or 89.43 kcal mol-1. This compares reasonably well with the value reported in the literature of 86.3 kcal mol-1[13].
Optimisation of the Chair and Boat transition states
Optimisation of the Chair transition state
An allyl fragement (fig. 6) was drawn in GaussView and and optimised at the HF/3-21G level[14]. The energy of this optimised structure was found to be -115.82304 Hartree.
Two of these optimised fragements were placed in the way shown below (fig. 7), such that the separation between the terminal CH2 units were separated by approximately 2.2 Å.
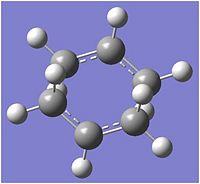
The structure was optimised to a transition state[15], computing force constants once, and the frequencies calculated, invoking Opt=NoEigen in order to prevent the calculation from crashing when a negative frequency was calculated. The energy of the transition state was calculated to be -231.619322 Hartree and an imaginary frequency was calculated at 817.92 cm-1 (818 cm-1), in perfect agreement with the values given in appendix 2, suggesting that optimisation has occurred to the correct structure. The optimised transition state structure is given in fig. 8.
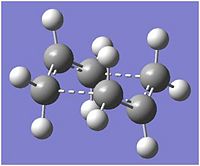
As viewed below, the imaginary frequency corresponds to the Cope rearrangement itself.
The carbon atoms numbered 3 and 14 approach each other and carbons 6 and 11 move apart. A double bond begins to form between 9 and 14 and the double bond previous between 1 and 3 breaks. The bond forming distance is 2.02053 Å and the bond breaking distance, 2.02066 Å.
Another method of optimising the transition state is the frozen coordinate method. In this method, the bond forming and breaking distances are fixed at a value of 2.2 Å while the rest of the structure is optimised[16]. Next the two bonds can be optimised[17] using the normal transition state optimisation without the need to compute force constants using the normal optimisation method.
The bond forming distance after this optimisation becomes 2.20001 Å and the bond breaking distance optimised to 2.19920 Å. This is slightly longer than the optimised distances found from the method where force constants, however the geometry of the two optimised structures is otherwise very similar. The bond angle between carbon atoms 3, 1 and 6 and 14, 9 and 11 is approximately 120o.
Optimisation of the Boat transition state
In order to optimise the boat transition structure, the reacant anti - 1,5-hexadiene (Ci) and product of the Cope reactant must be drawn with all atom labels directly corresponding between the structures as demonstrated below.
In the QST2 process, the system takes two molecules, an initial and final state (reactant and product), and optimises between the two to find a reasonable structure for the transition state. The result of the optimisation at HF/3-21G level is not however the correct transition state. This suggests that the method is quite dependant on the reactant and product structures provided. If the starting and finishing structures are altered as shown in fig. 9, the optimised transition state[18] shown below is obtained. The presence of one imaginary frequency at -840.09 cm-1 (-840 cm-1), in exact agreement with the appendix 2 and the energy (-231.602802 Hartree), also in exact agreement with the appendix, suggest that this result is the correct one.
File:Boat ts opt reactant and product 2 tb407.JPG
File:Optimised boat structure tb407.JPG
By examining the reactant and transition state geometries we can try to make a guess as to what the conformation of the final product will be when the reaction proceeds via a boat transition state and when it proceeds via a chair transition state.
By animating the imaginary (negative) frequency calculated, it is possible to see how the molecule moves during the Cope rearrangement.
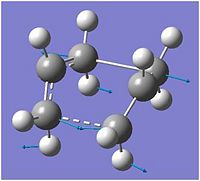
It can clearly be seen that the transition state is moving towards a C2 gauche structure (gauche4 or gauche2 in the appendix in this case rather than gauche1.)
In the case of the chair transition state, it is harder to tell towards which structure the transition state is moving. It appears that it is tending towards gauche3 or gauche5, both C1 structures, since the terminal carbons are pointing away from each other rather than in the same direction as in the case with the boat transition state. A method of predicting the final geometry of the product more definitively in this case is the Intrinsic Reaction Coordinate (IRC) method. The HF/3-21G optimised chair transition state was run using an IRC method with 50 points, computing the force constants once[19] to yield the final structure shown in fig. 11 in a total of 26 steps.

In order to complete the geometry optimisation, three different methods were used. First, a straightforward minimisation was run[20] on the final point of the IRC (fig. 11) to yield the structure shown in fig. 12.
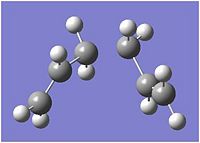
The energy of this optimised structure was found to be -231.69167 Hartree and, upon symmetrisation, the point group was found to be C2. This matches exactly with the appendix data for the gauche2 structure, suggesting that the Cope rearrangement proceeding via a chair transition state gives rise to the gauche2 conformer.
The second method used to complete the optimisation from the IRC was to simply run the IRC again using a greater number of points along the way[21] (7000.) This proved useless, since the system simply converged to exactly the same point as the system using points in 26 steps.
The final method used was to run the IRC again, calculating the force constants at every one of the 50 steps[22], rather than just once. This system converged in 47 steps to give a molecule with energy, -231.69167 Hartree, and point group C2 just like the optimisation on the final point of the initial IRC calculation.
Thus, calculating the force constants at each step of the minimisation helped to achieve the correct final structure as did optimisation of the final structure given in the IRC where force constants were computed only once. However, the computing time to calculate force constants at ever step is significantly longer than that to simply minimise the final point of an initial IRC calculation, particularly as the size of the system increases, and therefore where possible it is preferable to use the second method to try and establish to which conformer a transition state is moving.
Increasing the number of points in the calculation in this case had no effect on the accuracy of the final structure predicted and the system gave the same result with a maximum of 7000 steps as with 50. This is because in this particular case, the optimised structure was found in 26 steps. Since this is already well within the 50 steps allowed, it follows logically that increasing the number of steps avaiable will have no effect on the structure predicted.
Finding the Activation Energies of the Cope rearrangement
Calculating the Activation Energy of the reaction proceeding via a chair transition state
In order to calculate the activation energies, the frequencies of the transition states must be calculated and the thermochemistry data obtained compared with that of the Ci reactant molecule.
The chair transition state was optimised to a transition state (with opt=noeigen), calculating force constants once again only this time using the B3LYP/6-31G* method and basis set[23]. This returned a structure with an electronic energy of -234.556983 Hartree, in perfect agreement with the value reported in the appendix.
This optimised structure was then subjected to frequency calculations[24] at the same high level. The sum of the electronic and zero-point energies and the sum of electronic energies and thermal energies were calculated and found to be as follows:
Sum of electronic and zero-point Energies= -234.414930 Sum of electronic and thermal Energies= -234.409009
Recalling the same data from the frequency calculation of the reactant molecule (Ci anti 1,5-hexadiene molecule):
Sum of electronic and zero-point Energies= -234.469199 Sum of electronic and thermal Energies= -234.461855
All of these values are in extremely good agreement with those values published in the appendix of the exercise.
The activation energy at 0K is calculated by finding the energy difference between the electronic + zero-point energies for the transition state and the reactant.
Thus the activation energy at 0K for the Cope rearrangement proceeding via a chair transition state is given by the following:
-234.414930 - (-234.469199) = 0.054285 Hartree
This is equivalent to 34.06 kcal mol-1, in perfect agreement with the value listed in the appendix and very close to the the confidence limits for the experimental value.
The activation at 298.15 K is found in a similar way, substitutint the electronic plus zero-point energy terms for the electronic plus thermal energy terms.
Thus the activation energy at 298.15 K for the same process is given by:
-234.409009 - (-234.461855) = 0.052846 Hartree
This corresponds to 33.16 kcal mol-1, very close to the reported value for this calculation and within the confidence intervals for the experimental value, even though the experimental values are reported for 0 K. This suggests that even at values close to 0 K, which cannot truly be reached under experimental conditions, the energy of the molecule is affected by translational, rotational and especially vibrational energies.
Calculating the Activation Energy of the reaction proceeding via a boat transition state
The HF/3-21G Boat transition state was optimised and its frequencies calculated at the B3LYP/6-31G* level in the same way as the chair transition state above[25][26].
The thermochemistry data in the output was as follows:
Sum of electronic and zero-point Energies= -234.402342 Sum of electronic and thermal Energies= -234.396008
This data agreed perfectly with the values reported in the appendix of the exercise.
Taking the same values for the reactant molecule as before, the activation energies are calculated as follows:
For the reaction proceeding via boat transition state at 0 K:
-234.402342 - (-234.469199) = 0.066857 Hartree
This corresponds to 41.95 kcal mol-1 in good agreement with the reported value and reasonably close to the confidence intervals found for the experimental value.
For the reaction proceeding at 298.15 K:
-234.396008 - (-234.461855) = 0.065847 Hartree
This corresponds to 41.32 kcal mol-1, in perfect agreement with the calculated value given in the appendix and close to the confidence intervals for the experimental value.
Thus it can be safely stated that the Activation energies calculated using this method and basis-set are reasonably accurate, giving good agreement with literature for systems such as this. As the size of the system increases, the ability of the method and basis-set to model reality will drop however and thus, for large systems, a better method and basis-set is required.
References
- ↑ P. Atkins, J. de Paula, in Physical Chemistry, 2006, 8th edition, Oxford University Press, pp.392
- ↑ P. Atkins, J. de Paula, in Physical Chemistry, 2006, 8th edition, Oxford University Press, pp.392
- ↑ P. Atkins, J. de Paula, in Physical Chemistry, 2006, 8th edition, Oxford University Press, pp.338
- ↑ P. Atkins, J. de Paula, in Physical Chemistry, 2006, 8th edition, Oxford University Press, pp.392
- ↑ P. Atkins, J. de Paula, in Physical Chemistry, 2006, 8th edition, Oxford University Press, pp.392
- ↑ J.S. Binkley, J.A. Pople, W.J. Hehre, J. Am. Chem. Soc, 1980, pp.939
- ↑ http://hdl.handle.net/10042/to-4754
- ↑ http://hdl.handle.net/10042/to-4755
- ↑ http://hdl.handle.net/10042/to-4756
- ↑ http://hdl.handle.net/10042/to-4757
- ↑ http://hdl.handle.net/10042/to-4787
- ↑ http://hdl.handle.net/10042/to-4788
- ↑ J.M. Schulman, R.L. Disch, Chem Phys Lett, 1985, 113, pp.292
- ↑ http://hdl.handle.net/10042/to-4760
- ↑ http://hdl.handle.net/10042/to-4761
- ↑ http://hdl.handle.net/10042/to-4762
- ↑ http://hdl.handle.net/10042/to-4763
- ↑ http://hdl.handle.net/10042/to-4764
- ↑ http://hdl.handle.net/10042/to-4765
- ↑ http://hdl.handle.net/10042/to-4766
- ↑ http://hdl.handle.net/10042/to-4767
- ↑ http://hdl.handle.net/10042/to-4768
- ↑ http://hdl.handle.net/10042/to-4769
- ↑ http://hdl.handle.net/10042/to-4772
- ↑ http://hdl.handle.net/10042/to-4782
- ↑ http://hdl.handle.net/10042/to-4786