Rep:Module3:scastiglione1

Module 3: The Transition State

Computational Lab Module 3

S.Castiglione

Introduction

In this part of the computational lab, the transition structures of potential energy surfaces for the Cope rearrangement and Diels Alder cycloaddition reactions will be examined. In the first part, the tutorial, one will learn how to use the programs and methods required to do ones own investigation in the more challenging second part. In previous experiments smaller molecules were studied but here transition structures will be studied in larger molecules. Unlike in the previous sections we will be using molecular orbital-based methods, numerically solving the Schrodinger equation, and locating transition structures based on the local shape of a potential energy surface. Reaction paths and barrier heights can also be calculated. The previous molecular mechanics methods are not sufficient as they cannot describe bonds being broken and formed, and changes in bonding and electron distribution.

Part 1: Tutorial

Part 1.1: The Cope Rearrangement

Part 1.1.1: Introduction

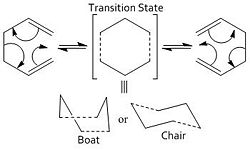
The Cope Rearrangement Of 1,5 Hexadiene

The Cope rearrangement of 1,5 heaxadiene will be examined to study chemical reactivity. The low energy minima and transition structres are to be found on the potential energy surface to find the preferred reaction mechanism. The reaction is a [3,3]-sigmatropic shift rearrangement (six electron process) and occurs via a concerted cyclic "chair" or a "boat" transition structure (pericyclic), where the "boat" transition is higher in energy. The 1,5-hexadiene can be in either the anti or the gauche form. Both these forms are optimised and their energy levels are compared.

Part 1.1.2: Optimizing The Reactants And Products

For reference and analysis the table from appendix 1 is recreated here with images and values from my own investigations;

Conformer	Structure	Point Group	Energy/ Hartrees HF/3-21G	Relative Energy /kcal/mol
gauche1		C2	-231.688	3.10
gauche2		C2	-231.692	0.62
gauche3	File:Gauche3drawing.jpg	C1	-231.693	0.00
gauche4	File:Gauche4drawing.jpg	C2	-231.692	0.71
gauche5	File:Gauche5drawing.jpg	C1	-231.690	1.91
gauche6		C1	-231.689	2.20
anti1		C2	-231.693	0.04
anti2		Ci	-231.693	0.08
anti3		C2h	-231.689	2.25
anti4		C1	-231.691	1.06

Image Of Optimised 'Anti 1' Conformer

Image Of Optimised 'Gauche 1' Conformer

Firstly several structures will be optimized, symmetrized it to find the point groups, the vibrational frequencies will be calculated and visualized and potential energies will be calculated and compared with experimental values.

An antiperiplanar 1,5, hexadiene was drawn and optimised using the Hartree Fock method and 3-21G basis set. The optimised structure has C₂ point group symmetry and an energy of -231.6926 Hartrees. This is the 'anti1' form shown in the table in appendix 1 . The appendix gives the calculated energy of this conformer is -231.69260 Hartrees which is a great match and agrees with the point group symmetry.

A gauche conformer was modelled next. The same method and basis set were used. I would expect the gauche molecule to be higher in energy than the anti conformer as sterically the groups would ideally be furthest away from each other as possible. The energy of the gauche ('gauche 1') conformer is -231.6877 Hartree and its symmetry is C₂. This is a higher (more positive) energy than shown by the anti conformer , as expected. Of course there is a possibility for rotation in these molecules but it would seem that it is more likely the molecule will adopt an anti conformation. The anti conformation has less steric interactions and so is more stable.

Most of the lowest energy conformers in appendix 1 are the anti conformers with the exception of the 'anti 3' and 'anti 4' which are comparatively higher in energy and the 'gauche 3' conformer which is comparatively low in energy. The two anti forms have one of the alkene groups pointing pout of the molecule general plane. These groups will sterically interact with hydrogens on the other sections and destabilise the molecule. The gauche 3 molecule is more stable most likely due to the sigma C-H bonding, pi star C=C antibonding orbital overlap known to occur in this configuration. In this particular gauche configuration has most of these possible stabilising overlaps, whilst the gauche 2 and 4 conformers have some also (but fewer) and so are slightly stabilised.

Jmol rotatable molecules.

Press the buttons below to open up Jmol files for the molecule.

Comparison Of Structures
(energy in Hartrees, bond lengths in angstroms, angles in degrees)

Value	HF/3-21G	B3LYP/6-31G*
Energy	-231.693	-234.612
C=C Bond Lengths	1.32	1.33
Outer C-C Bond Lengths	1.51	1.50
Centre C-C Bond Length	1.55	1.55
C1-C2-C3 and C4-C5-C6 Angle	124.8	125.3
C2-C3-C4 and C3-C4-C5 Angle	111.3	112.7
C1-C2-C3-C4 and C3-C4-C5-C6 Dihedral Angle	114.6	118.8
C2-C3-C4-C5 Dihedral Angle	180.0	180.0

The C_i 'anti 2' molecule was next to be optimised using the same method and basis set as before and then using the B3LYP/6-31G* DFT level, a higher level of theory . Both has C_i symmetry and their properties are summarised in the table to the right.

The value obtained is the same as that in the appendix (for the HF optimisation), as is the point group. For the higher level of theory the energy is more negative and also matches that in the table. For the higher level of theory the energy is found to be more negative however really we should not compare across theory levels. Whilst the symmetry remains the bond lengths change with only the central C-C bond length remaining the same .Whilst the central dihedral angle is the same in both the other angles differ, being larger for the B3LYP/6-31G* optimised structure in which the groups are more spread out. This greater spreading will reduce steric instability possibly accounting for the lower energy.

Jmol rotatable molecule.

Press the buttons below to open up Jmol files for the molecule.

Part 1.1.3: Frequency Calculations

File:Noimagvibs.jpg

A frequency calculation was next run at the B3LYP/6-31G* theory level to visualise the vibrations of the molecule and check that the molecule is a genuine minimum and not a transition state. There are no imaginary vibrations so the molecule is at a global minimum . The energy is the same as that given for the optimisation at this theory level, as expected. The non-fingerprint region high intensity vibrations are shown in the table and assigned. The computed IR spectrum is also presented.

Thermochemical properties can also be examined using this calculation.
The energies calculated would be for room temperature, i.e. 298.15 K.
The reference values given are from the table in appendix 2 and energies are quoted in Hartrees.

Selected Vibrations Of 'anti 2' 1,5 hexadiene

Frequency /cm-1	Image	Intensity	Assignment
1734		18	C=C Stretch
3031		54	Alkane C-H Stretch
3080		36	Alkane C-H Stretch
3136	File:3136.gif	56	Alkene C-H Stretch
3156	File:3156.gif	15	Alkene C-H Stretch
3234		45	Alkene C-H Stretch

IR Spectrum Of 'anti 2'

The electronic energy was calculated to be -234.6117 Hartree, the same as in the literature.

The sum of electronic and zero point energies (energy at 0K , E=E_elec + ZPE) was calculated to be -234.4692 Hartree.

The sum of electronic and thermal energies ( E=E + E_vib + E_rot + E_trans)was calculated to be -234.4618 Hartree (Ref: -234.4619 Hartree).

The sum of electronic and thermal energies with correction for room temperature was -234.4609 Hartree.

The sum of electronic and thermal free energies including entropic contribution to free energy was -234.5008 Hartree.

Recalculation at 0 degrees Kelvin gave the same values.

The good agreement between the calculated and reference values indicate the calculations have been performed correctly. The electronic energy is more negative than the other 4 values so one would expect the zero-point energy, thermal energy, thermal enthalpy and free energy to be positive in value.

Part 1.2: The Chair And Boat Transition Structures

Part 1.2.1: Introduction

Transition structure optimizations will be set up in this section and the "chair" and "boat" transition structures for the Cope rearrangement will be examined. Both consist of two C₃H₅ allyl fragments positioned approximately 2.2 Å apart, one with C₂h symmetry and the other with C₂v symmetry.

Part 1.2.2: Optimising The Chair Transition Structure

Firstly, one allyl fragment of CH₂CHCH₂ is optimised at the HF/3-21G level of theory. A guessed chair transition state was drawn using two of the optimised allyl fragments separated by a distance of 2.2Å. This was then optimised at the HF/3-21G level of theory using two different methods as described below.

Part 1.2.2.1: Hessian/ TS Berny Method

File:Chairtsbimage.jpg

Chair TS Imaginary Vibration

The guessed transition state is optimised using the TS berny method and a frequency calculation was run simultaneously (HF/3-21G level of theory). The TS berny method calculates the reaction coordinate by computing the force constant matrix. The theoretical to-be-formed bonds are 2.021 Angstroms in the transition state and there is an imaginary frequency of magnitude 818 cm^-1 as expected. This vibration (shown) corresponds to the cope rearrangement showing the formation of the one sigma C-C bond and the breaking of the one opposite it. The negativity of the frequency indicates this is a transition state. Looking at the thermochemistry values the Electronic energy is -231.619 Hartree, as in Appendix 2. The sum of electronic and zero-point energies (-231.467 Hartree) and the sum of electronic and thermal energies (-231.461 Hartree) are also both the same as given in the appendix, suggesting the calculations have been successful.

Jmol rotatable molecule.

Press the buttons below to open up Jmol files for the molecule.

Part 1.2.2.2: Frozen Coordinate Method

Chair TS

Now we will try optimizing the transition structure again using the frozen coordinate method. The guessed TS is first optimised like a minimum and the breaking/forming bonds are fixed at 2.2 Angstroms. This bond length is then unfrozen and the TS optimisation is performed without calculating force constants.Looking at the new thermochemistry values the Electronic energy is once again -231.619 Hartree, as in Appendix 2. The sum of electronic and zero-point energies (-231.467 Hartree) and the sum of electronic and thermal energies (-231.461 Hartree) are also both the same as given in the appendix. These values are the same as in the previous calculation. The optimised structure looks the same as found using the first method. The imaginary frequency is still at -818 cm^-1 which, like in the first optimisation, corresponds to the Cope Rearrangement. The C-C bond breaking and bond forming bond lengths are 2.02 Angstroms. This is the same as for the previous optimisation. The two methods seem to converge to a single optimisation, unsurprising given the simple fragments and limited conformational freedom.

Jmol rotatable molecule.

Press the buttons below to open up Jmol files for the molecule.

Part 1.2.3: Optimising The Boat Transition Structure

File:Boattsqts2image.jpg

A boat TS will now be calculated using a different method, a QST2 calculation.

Part 1.2.3.1: QST2 Method

File:Boatfreqimagin.gif

The optimised boat transition state is calculated from two different C_i 'anti 2' conformers of 1,5-hexadiene by interpolating the two structures until they reach the transition state. The atoms on both structures must be labelled correctly and some of the dihedral and bond angles are modified. This must be done before a QST2 calculation at the HF/3-21G level of theory is performed or the calculation will fail. The C-C breaking/forming bond lengths are 2.14 Angstroms here, larger than in the chair TS. There is an imaginary vibration at -840cm^-1 confirming this is a transition state. The vibration is consistent with the rearrangement with the formation of the one sigma C-C bond and the breaking of the one opposite it with the necessary bond changes. The boat TS has a C₂v point group. Looking at the thermochemical properties and comparing them to Appendix 2 there is a good correlation. The electronic energy is -231.6603 Hartree, as in Appendix 2. The sum of electronic and zero-point energies (-231.451 Hartree) and the sum of electronic and thermal energies (-231.445 Hartree) are also both the same as given in the appendix, suggesting the calculations have been successful and the QST2 calculations have been done correctly and the optimised structure is good.

Jmol rotatable molecule.

Press the buttons below to open up Jmol files for the molecule.

Part 1.2.4: IRC For The Chair Transition Structure

It is almost impossible to predict which conformer the reaction paths from the transitions structures will lead to. However, we can follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface. This can be done by looking at the Intrinsic Reaction Coordinate. This type of calculation takes a transition state and then takes small geometrical steps in the direction of the steepest slope of the potential energy surface looking for the conformers to which the TS connects. Since the reaction coordinate is symmetrical, the IRC calculation is performed in the forward direction only, with force constants calculated once and for 50 points. Next, the last found geometry was optimised using the HF/3-21G level of theory, creating what should be the right geometry, a C₂ gauche-esque molecule. The IRC calculation is stopped before a geometry with the minimum energy as the gradient of the potential energy graph is assumed to be small enough to be considered as a minimum. There are three methods to improve this, as detailed below. The first involves restarting the IRC with more points (I tried 150), however it stops at the same point as before. The second option involves using the last point found in the first calculation and optimising to a minimum. The energy of this molecule is -231.692 Hartree and the point group is C₂, corresponding to the 'gauche 2' conformer. We can also calculate the force constant every step of the way. Previously, the force constant was calculated at the start of the calculation and assumed henceforth. When it is calculated at every step, once the global minimum is reached it stops. The final result was the same as before.

Part 1.2.5: IRC For The Boat Transition Structure

The same optimisation was carried out for the boat transition state. The energy of the boat TS is -231.685 Hartree. It's a very high energy structure and doesn't correlate very well with any of the tabulated structures. It is possible that this method can be improved on by using the QST3 method in which a guess for the TS is entered into the calculation but I have not done this as the very high energy would indicate that it is most likely that the TS goes via the chair.

Part 1.2.6: Activation Energies For The Transition Structures

Comparison Of Boat And Chair TS At Different Theory Levels

	Chair	Chair	Boat	Boat
Value	HF/3-21G	B3LYP/6-31G	HF/3-21G	B3LYP/6-31G
Electronic Energy / Hartree	-231.619	-234.557	-231.603	-234.543
Sum of Electronic and Zero-Point Energies / Hartree	-231.467	-234.415	-231.451	-234.402
Sum of Electronic and Thermal Energies / Hartree	-231.461	-234.409	-231.445	-234.396
Breaking/Forming C-C Bond Length / Angstroms	2.02	1.97	2.14	2.21
C=C Bond Length / Angstroms	1.39	1.41	1.38	1.39
C-C-C Angle / Degrees	120	120	122	122
Imaginary Frequency / cm-1	-818	-566	-840	-530
Symmetry Point Group	C1	C1	C2v	C2v

Finally the activation energies for the reaction via both transition structures will be calculated. For this, the transition structures need to be reoptimised at the B3LYP/6-31G* level of theory and frequency calculations were run also. It is then possible to compare the structures for both levels of theory. The geometries are quite similar but the energy differences are much greater. The point groups for the chair and boat are the same irrespective of method used. The imaginary frequencies are very different depending on the theory level used but both vibrations correspond to the same transition for the Cope rearrangement. In both cases the boat is shown to be less stable and the energies correspond well to those in the given appendix.

Using the thermochemical values calculated at the B3LYP/6-31G* level of theory, we can calculate the activation energy for the Cope Rearrangement of 1,5-hexadiene. We can do this by observing the difference between the transition structure and the starting product (assumed to be the 'anti 2' conformer from the first part). We need to compare the sum of electronic and zero-point energies to give us the activation energy at 0k. For the chair conformer this gives 34 kcal/mol and for the boat conformer 42 kcal/mol (ref are 33.5 ± 0.5 kcal/mol via the chair transition structure and 44.7 ± 2.0 kcal/mol via the boat transition structure ). The activation energy is higher for the boat than the chair so the reaction will proceed via the chair transition state due to the lower activation energy.