Rep:Module3:rp1207
Module 3
During this module transition structures for different reactions were characterised on potential energy surfaces. Their energies, MO's and geometries were studied in order to gain a fuller knowledge of the way in whic hthe reactions proceed.
For the entirety of this project unless otherwise stated energies will be written in atomic units (hartree) and "The Script" or "appendix 1 and 2" both can be found at https://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3 as provided for this course.
The Cope Rearrangement
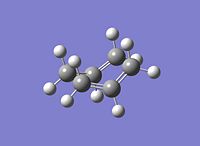
During this project the cope rearrangement of 1,5-hexadiene was used as an example of a chemical reactivity problem. This corresponds to a concerted 3,3-Sigmatropic rearrangement of the molecule as shown;
The low-energy minima and transition structures of the molecule were located on a potential energy surface and this information was used in order to determine the preferred reaction mechanism. Firstly the antiperiplanar and gauche structures were optimised using a Hartree Fock method with a 3-21G basis set, the output structures were then symmetrised to determine their point group this could also be used for comparison with the appendix 1 in order to determine the geometry of the molecules. The results of the optimisation are shown in the table below;
| Property | Antiperiplanar | Gauche |
|---|---|---|
| Calculation Type | FOPT | FOPT |
| Calculation Method | RHF | RHF |
| Basis Set | 3-21G | 3-21G |
| Energy a.u | -231.69166702 | -231.69260231 |
| RMS Gradient | 0.00002084 | 0.00000883 |
| Dipole Debye | 0.2019 | 0.3804 |
| Point Group | C2 | C2 |
| Image |  |
|
The table shows that the RMS gradient has converged to <0.0001 therefore can be assumed to be complete to a good degree of accuracy. As can be seen from the table the energies of the Gauche and Antiperiplanar molecules are very similar however it can be seen that the Guache molecule has a slightly lower energy than the Antiperiplanar equivelent.
Upon comparison with the energies, point groups and images in Appendix 1 it was concluded that the antiperiplanar molecule formed in this part of the experiment was the Anti 1 and the gauche the Guache 2 isomer.
The Ci Anti2 Isomer
The Anti 2 Ci molecule as found in the appendix was modelled using Guassview and optimised using the 3-21G basis set then the method was altered and it was calculated using the 6-31G basis set, the results of the two optimisations and the energy from the Appendix 1 are shown in the table below;
| Property | 3-21G | 6-31G |
|---|---|---|
| Calculation Type | FOPT | FOPT |
| Calculation Method | RHF | RB3LYP |
| Basis Set | 3-21G | 6-31G |
| Energy a.u | -231.69166702 | -234.55970424 |
| Lit Energy a.u | -231.69166702 | -231.69166702 |
| RMS Gradient | 0.00002084 | 0.00004646 |
| Dipole Debye | 0.2019 | 0.0000 |
| Point Group | Ci | Ci |
| Image |  |
|
As can be seen from the above table the 3-21G optimisation shows perfect agreement with the energy output seen in the appendix(-231.6966702a.u.) however the higher level optimisation has reached a lower optimised energy. This suggests that the 6-31G higher level of optimisation has altered the geometry of the molecule slightly in order to find a more stable product, this can seen seen in the above images as the structures can be seen to be almost identical. The similarity of the two outputs suggests that the 3-21G basis set is a good approximation for energy calculations.
Ci Frequency Calculation
The optimised B3LYP/6-31G structure was used to calculate the vibrations for the 1,5-hexadiene molecule. No imaginary frequencies were observed in the output allowing the assuption that the molecule had been optimised andfrequencies calculated to a good level of accuracy.
From the output file it could be seen that;
(i) The sum of the electronic and zero point energies were; -234.416244 a.u.
(ii) The sum of the electronic and thermal energies were;-234.408954 a.u.
(iii) The sum of the electronic and thermal enthalpies were; -234.408010 a.u.
(iv) The sum of the electronic and thermal free energies were; -234.447849 a.u.
These values will be used later in order to calculate activation energies.
Optimising Chair and Boat Transition States
The 'chair' and 'boat' structures are generally accepted to be the two possible transitoon states for the Cope rearrangement of 1,5-hexadiene. In this section these two forms of the transiton state were optimised and the frequecy analysis calculated using Guassian.
Via these optimisations the activation energies for each possible mechanism were calculated and compared.
Initially the CH2CHCH2 allyl structure was optimies using Hartree Fock 3-21G level of theory in order to be used in the continuing transition state optimisations.
This optimised structure was copied twice into a new window and were orientated to approximately the chair transition state, the terminal ends of the allyl fragments were orientated such that they were 2.2Å apart but were not fixed in this orientation.
High Level Optimisations
Upon use of high level optimisations a comparison of the chair and boat transition states were compared in order to determine the direction of the reaction. The transition state energies are compared in the table below;
| Tansition State | Chair | Boat | |
|---|---|---|---|
| Energy a.u | -231.69253524 | -234.55970724 | |
| RMS Gradient | 0.00002583 | 0.00004646 | |
| Dipole.Debye | 0.0006 | 0.0000 | |
| Point Group | C1i | C1i | |
| Image |  |
 |
The chair and boat transition states were optimised in two different ways in order to illustarate the accuracy of both, as well as the strengths and weaknesses of both.
The chair transition state was optimised by computing the foce constant matrix, this is the easiest of the two methods although requires an input 'guessed' transition state, whcih, if too far from reality will not produce a reasonable outcome. The guessed transition state was optimised to a Hartee Fock method and 3-21G Transition State(Bery) and the frequency calculated simultaneously. The vibrational output was used to show that a transition state had been formed and is discussed below.
The boat transition state was calculated usign the QST2 method. Although more time consuming and complex than the method used for the chair conformation the this method does not require an accurate guess transition state instead the reactant and the product molecule for a reaction are used and the transition state is calculated as an intermediate between these two molecules. The two molecules were modelled and labelled so that the atoms in the reagent and product correspond as they would in the reaction. The opt+freq calculation was then carried out as with the chair transition state optimisation however instead of TS(berny) the TS QST2 was used.
Upon fist attempt this calculation failed as the calculation simply attempts to linearly bind the two fragments and does not take a possible C-C central bond rotation into account, the dihedral angle in the molecule was then altered in the reactant and product molecules so that this gerometry could be accounted for, the optimisation was send to run again and the boat transition state was optimised. The optimised transition states are shown below;
As can be seen from the diagram below, the imaginary frequencies from both the boat and transition state correspond to the Cope rearrangement this confirms that the structures optimised are the correct transition states;
| Tansition State | Chair | Boat | |
|---|---|---|---|
| Frequency cm-1 | -565.46 | -530.58 | |
| Image |  |
 |
Confomer Determination-Intrinsic Reaction Coordinate (IRC) Calculation
Although it is useful to have the transition states optimised and frequencies calculated it is impossible to determine which conformers of 1,5-hexadiene these refer to. The Intrinsic Reaction Coordinate (IRC) calculation can be used to find a reaction path which takes the transition state to a local minimum by creating a series of points by small geometry alterations.
This calculation can be confimred to have completed to a good optimisation By ensuring that it has reached a minimum geometry ( RMS gradient should have gone to zero) at a first approximation this has not occured as not enough poitns have been calculated alogn the IRC gradient (50). In order to improve this the IRC was recalculated with double the number of points calculated.
The IRC was calculated for the chair conformation and the RMS gradient was seen to go to zero;
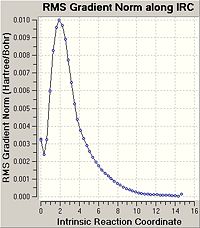
The computed minima is as seen in the diagram to the left.
A simple comparison of the energy of this stuructre which was read from the summary file to be = -231.69165584 and its geometry with the appendix file shows that this structure corresponds to the Guache 2 structure.
Activation Energy Calculations
The activiation energies for both transition structures were calculated by reoptimising the chair and boat transition states to a B3LYP 6-31G basis set and carrying out frequency calculations starting at the previously calculated Hartree Fock 3-21G basis set calculations.
The results of these optimisations are shown below;
| --- | Chair | Boat |
|---|---|---|
| Calc Type | Freq | Freq |
| Method | RB3LYP | RB3LYP |
| Basis Set | 6-31G | 6-31G |
| Charge | 0 | 0 |
| Total Energie a.u. | -234.55698284 | -234.54309303 |
| RMS Gradient | 0.00006361 | 0.00001057 |
| Dipole Moment | 0.0000 | 0.0614 |
Vibrations
| --- | Chair | Boat |
|---|---|---|
| Frequency | -565.46 | 530.58 |
| Infrared | 0.0828 | 0.3347 |
| Image | |
|
As each transitoopn state has only one imaginary vibration which corresponds to the reaction then it can be assumed that the optimisation calculation has been completed to a good level of accuracy.
In order to calculate the activiation energies of the transition states the optimisation energies of the start products are taken away from the transition state energies to calculate the activation energies.
| --- | HF/3-21G Electronic Energy (a.u.) | HF/3-21 Sum of electronic and zeropoint energies (a.u.) | Hf/3-21 Sum of electronic and thermal energies (a.u.) | B3LYP/6-31G* Electronic Energy (a.u.) | B3LYP/6-31G* Sum of electronic and zeropoint energies (a.u.) | B3LYP/6-31G* Sum of electronic and thermal energies (a.u.) |
|---|---|---|---|---|---|---|
| Chair | -231.61932207 | -231.4666693 | -231.461332 | -234.55698285 | -234.414919 | -234.408998 |
| Boat | -231.60280231 | -231.450926 | -231.445298 | -234.54309304 | -234.402339 | -234.396006 |
| Reactant (anti2) | -231.69253524 | -231.539540 | -231.532566 | -234.61171 | -234.46920 | 234.46185 |
| --- | HF/3-21G 0K | HF/3-21 298.15K | B3LYP/6-31G* 0K | B3LYP/6-31G* 298.15K |
|---|---|---|---|---|
| ΔE Chair (Kcal Mol-1) | 45.73 | 44.70 | 34.06 | 33.17 |
| ΔE Boat(Kcal Mol-1) | 55.61 | 54.76 | 41.96 | 41.28 |
As literature sites the experimental activation energies to be 33.5 ±0.5 Kcal mol-1 for the chair transition state and 44.7±0.2 Kcal mol-1 at 0K (as seen in the script) it can be seen that the 3-21G basis set underestimates the activation energy to a reasonable degree whereas the more accurate B3LYP 6-31G produces a good prediction-although for the boat structure this underestimates the activation energy slightly. The inaccuracy for the 3-21G may be due to the lower level of the calculation which suggests a slightly less stable transition state than the higher level method.
Diels Alder
During this part of the report two simple Diels-Alder reactions will be analysed. 1) The cycloaddition of butadiene and ethene. 2) The regioselectivity of the Diels-Alder reaction between Cyclohexa-1,3-diene and maleic anhydride
Butadiene and Ethene
The structure of the cis-butadiene molecule was optimised using the AM1 semi-empirical molecular orbital method. The MO's were visualised and their geometries determined, these and the images corresponding to them are shown for evidence in the table below;
| MO | HOMO | LUMO |
|---|---|---|
| Symmetry | antisymmetric | symmetric |
| Image |  |
|
As can be seen from the above table the geometries of the MOs with respect to the indicated plane are HOMO=antisymmetric and LUMO=symmetric. As Ethylene has a Symmetric LUMO, which refers to its occupied π bond and a Antisymetric HOMO, reffering to its unoccupied π* bond then this shows that the, HOMO Cis-Butadiene + LUMO Ethylene = Symmetric therefore interact as they have the same geometry. LUMO Cis-Butadiene + HOMO Ethylene = Antisymmetric therefore may interact.
It is expected that in the Diels-Alder reaction the orbitals with the same symmetry elements will overlap via an 'allowed' reaction.
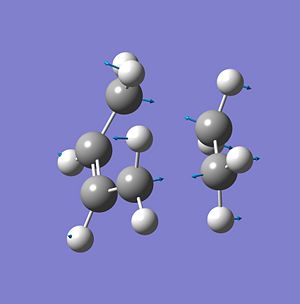
The transition state for this reaction was produced by calculating the force constant matrix, this was possible as there is a good level of understandign of this reaction, including the expected product therefore a good approximation of the actual transition state can be made and optimised to produce a computed more accurate equivalent. This was produced by modelling the final product and then 'breaking' the C-C bonds that join the two reactant molecules together lengthening the atom distances to 2Å to produce an approximate guess of the transition state. The transition state was them optimised to a TS (bernie) and the calculated geometry produced. The geometry produced appeared as expected with the two molecules within a reasonable semi-bond forming distance-distance between the two pairs of bond formnig C-C atoms=2.11878-2.11949Å.
As well as the geometry another way to confirm that the transition state has been accurately calculated is by using the frequency calculation which was calculated simultaneously with the optimisation. As expected there was only one imaginatry frequency and when this was visualised it was seen to correspond to the diels alder reaction as seen in the image below;
The transition state HOMO and LUMO were visualied and are seen in the table below;
| MO | HOMO | LUMO |
|---|---|---|
| Symmetry | antisymmetric | symmetric |
| Image |  |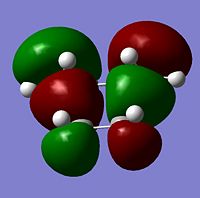
|
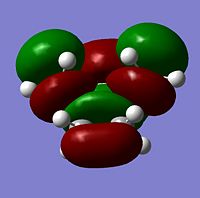
As can be seen the transition state molecule has the same HOMO and LUMO geometry as the cis-butadiene.
The LUMO molecules orbitals are seen to have mode nodes than the HOMO which explains the higher energy of the LUMO compared to the HOMO.
Regioselectivity of Diels Alder Reaction
The regioselectivity of the facile reaction between Cyclohexa-1,3-diene and maleic anhydride can be explained using molecular modelling and comparison of the relative transition state molecules. It is known that the endo product is the main product of this reaction.
In order to achieve this the transition states were using ChemBio3D and guassview and optimised using the 3-21G basis set followed by the 6-31G for accuracy. The vibrations for these optimisations were also calculated in order to confirm that a transition state has been modelled, the expected outcoem for each optimisation was one imaginary frequency correspondign to the reaction. The energy and other propetries of these transition state calculations are shown in the table below;
| --- | Endo | Exo | |
|---|---|---|---|
| Calc Type | Freq | Freq | |
| Method | Freq | RB3LYP | |
| Basis Set | 6-31G | 6-31G | |
| Charge | 0 | 0 | |
| Total Energie a.u. | -612.49547768 | -612.49098152 | |
| RMS Gradient | 0.00001013 | 0.00000556 | |
| Dipole Moment | 7.0087 | 6.3934 |
As can be seen from the above table the endo transition state can be seen to have a more stable structure as it's total energy is lower than that found for the exo structure. Therefore supports the reasoning that the endo product is the kineticly favoured product. The reasons for this relationship were further analysed and discussed below. The energy calculations for these transition states are comparitable as both transition states have the same number and types of atoms and were optimised to the same level of theory.
Endo Product;
Calculated Bond Lengths;
| Atoms | Bond Length (Å) |
|---|---|
| partly formed σ C-C | 2.16236 |
| partly formed σ C-C | 2.16244 |
| maleic C=O and cyclohexene-C bond length | 2.89227 |
| maleic C=O and cyclohexene-C bond length | 2.89216 |
Exo Product;
Calculated Bond Lengths;
| Atoms | Bond Length (Å) |
|---|---|
| partly formed σ C-C | 2.17614 |
| partly formed σ C-C | 2.17865 |
| maleic C=O and cyclohexene-C bond length | 2.93365 |
| maleic C=O and cyclohexene-C bond length | 2.93439 |
As can be seen from the above tables the endo transition state has a shorter maleic C=O to cyclohexene this related to this transiton state having a higher steric strain than the equivelent boat transition state. Despite this the endo transition state is known to be the major transition state, this will be discussed laster in the MO discussion.
Van Der Vaals Radii
Standard van der waals radii for the atoms found within this reaction are shown below;
| Atoms | Bond Length (Å) |
|---|---|
| C | 1.70 |
| O | 1.52 |
| H | 1.20 |
Typical C-C bond lengths for sp3 hybridised molecules are =1.55Å and =1.38Å for sp2 hybridied molecules.
Although it can be seen that the distance between both partically formed C-C bonds are shorter than the combined C van der vaals radii confirming that the bond between them is partically formed it can also be seen that they are longer than the standard Sp3 orbital that they become, they are also very similar in length suggesting that the bonds form almost simultaneously.
References
1. Bondi, A. (1964). "Van der Waals Volumes and Radii". J. Phys. Chem. 68 (3): 441–5 -van der waals 2. R. S. Rowland & R. Taylor, J. Phys. Chem., 100, 7384 - 7391, 1996 -van der waals H 3. J. Phys. C: Solid State Phys. 19 (1986) 4613-4621. -typical bond lengths
Molecular Orbital Analysis
| --- | Endo | Exo | |
|---|---|---|---|
| HOMO Energy (a.u.) | -0.24809 | -0.24742 | |
| HOMO Image |  |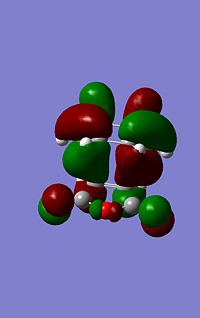
 |
|
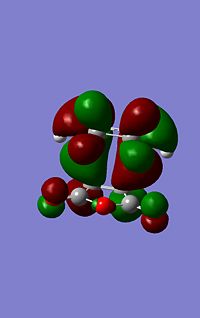| LUMO Energy (a.u.) | -0.08085 | -0.09163 | |
| LUMO Image |  |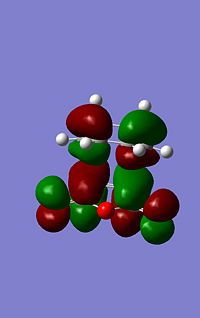
 |
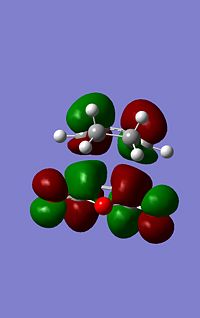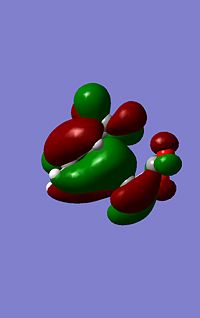
As can be seen from the images to the left the endo structure shows a secondary orbital overlap, a secondary orbital overlap refers to1 the overlap of orbitals that were not involved in the overall reaction, in this case thsi feres to the (C=O)-O-(C=) molecular orbitals with the above C-C orbitals. This extra stabilisation is reflected in the slightly increased stability of the endo HOMO. Althoug this interaction cannot be quantified using this analysis.
The secondary overlap interaction for the endo product however is likely to outwiegh the steric hinderence discussed above causing the transition state to be mroe stable and tehrefore the most kinetically prefered.
These calculations do not take dipole moments of the transition states into account, large dipole moments destabilise the molecule and therefore contribute to the overall energy contribution of the molecule.