Rep:Module3:physicalwm207
This module is primarily concerned with analysing transistion states via computational methods; specifically the Cope Rearrangement and the Diels-Alder Cycloaddition
The Cope Rearrangement

The Cope Rearrangement is a well known reversible reaction that requires a specific high-energy conformation to proceed. Hopefully we can learn about this reaction by analysing the conformations of Hexadiene and the possible transition states involved in the reaction.
Optimising Hexadiene
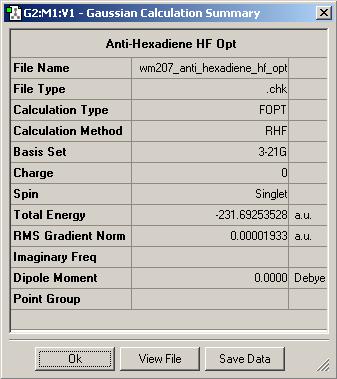
Hexadiene was first created in Gaussview with an anti-peri-planar (APP) arrangement as this is commonly assumed to be a low energy conformation. The molecule was optimised with a Hartree-Foch method using the 3-21G basis set.
This initial optimisation was later identified as anti2 in the Appendix provided in the Mod:phys3 wikipage. Although it is interesting to note that the submitted conformation was closer to that of anti1.
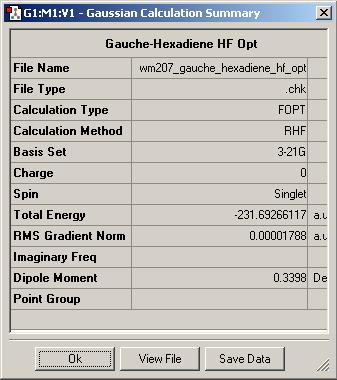
The anti2 optimised molecule was then edited by changing the torsion angle between C2-C3-C4-C5 from 180 degrees to 60 degrees, otherwise described as a gauche conformation. This molceule was optimised as before using Hartree-Foch and 3-21G; it was then identified using the Appendix as gauche3.
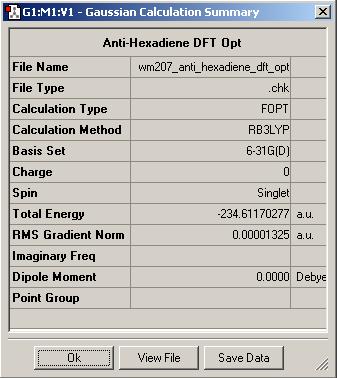
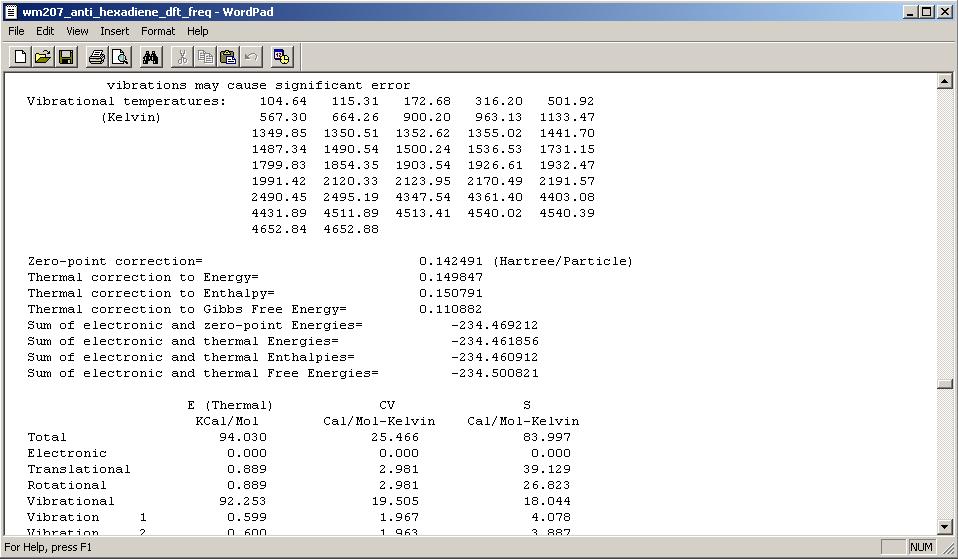
Finally, the anti2 molecule was re-optimised at a higher (DFT/B3LYP/6-31G*) level and the results can be compared to the HF/3-21G method below
| Gauche3 | Anti2 | Anti2 |
|---|---|---|
 |
 |
|
Comparisons of the output summaries shows that the Hartree-Foch anti2 conformation is indeed lower in energy than its gauche conterpart, as expected, but the DFT optimisation gives a substantially lower energy compared to the Hartree-Foch Optimisation. This serves to highlight the importance in only comparing energies for molecules optimised at the same level as calculations run at different levels of accuracy can vary quite widely.
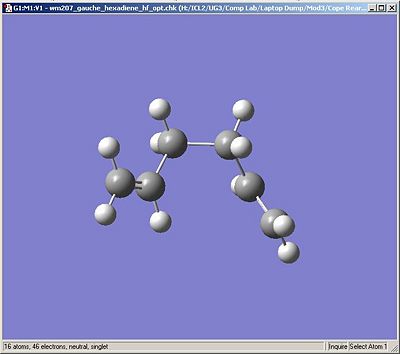
Below are the output images of the optimised molecules for comparison with the Appendix.
| Gauche3 | Anti2 |
|---|---|
 |
|
| C1 Symmetry | Ci/C1 Symmetry |
Finally, the output log file of the frequency calculations detailing the Thermochemistry:
Creating the Transition State
Whilst analysing straight chains has given us some idea of their natural energies it does not tell us how the Cope Rearrangement takes place. Whether the rearrangement is concerted or stepwise, it will have to go through a cyclic intermediate and presumably a six-membered cyclic structure can have either a chair or boat conformation.
The Chair Transition State
The chair conformation was created by optimising an allyl fragment which was subsequently placed close to an exact duplicate with an approximate orientation to produce a chair transition state. Specifically the two fragments were placed so that the two bond forming/breaking distances were 2.2 angstroms. The manually-edited structure was then subjected to an optimisation and frequency calculation, optimising to a transition state (TS Berny) for which the force constants were calculated once. This and all previous optimisations were done with a Hartree-Foch/3-21G method. The Keyword opt=noeigen was also added as one imaginary frequency was expected and this should prevent the calculation from crashing.
The output did contain an imaginary frequency which related to the forwards/backwards direction of the reaction, although the suggested optimum bond distance between the allyl fragments of 2.2 angstroms had been reduced to 2.02 angstroms. As an error was suspected the calculation was re-run with the allyl fragments 2.3 angstroms apart but this had no impact on the output and the shortening of the bond proved to be the case for all subsequent calculations as well.
An alternative, slightly more cautious, approach can be used by freezing the bonds being formed/broken so that the rest of the transition state is perfectly optimised before the bonds are then included in calculations. The Redundant Coordinate Editor was used to freeze the bonds and the transition state was optimised as before, although the force constants were not calculated and opt=modredundant had been included in the keywords. The result was then re-edited with the coordinate editor changing the bonds from frozen to derivative so that they would be included in the calculations. This inclusive transition state was optimised as a TS Berny, but the force constants were not calculated as the derivative bonds used a guess Hessian.
The results of the two methods were extremely similar, with bond lengths equal to within a picometre and bond angles differing by no more than a tenth of a degree. Images for comparison are included below and a display of the imaginary vibration which indicates the direction of the reaction.
| Method 1 | Method 2 | Imaginary Vibration |
|---|---|---|
 |
 |

|
The Boat Transition State

In this example, instead of creating the transition state manually and having Gaussian optimise it, Gaussian will be provided with a reactant and a product molecule and asked to find the transition state between them. The anti2 hexadiene created in the first part, is used as a starting point. The chain is added twice to a molceule group, in seperate windows, and then numbered according to the reaction mechanism. It was necessary to have the carbon atoms numbered in the correct order but also the hydrogen atoms needed to be numbered in the same order to maintain their relative orientation otherwise the calculation would hit difficulties very quickly. It was also necessary to manipulate the chains towards a reactive conformation, in the optimised anti2 chain the reactive chain ends are held as far away from each other as possible and subsequently will not react in this conformation. So the torsion angle across C2-C3-C4-C5 was edited from 180 to 0 degrees and the C1-C2-C3 (and C4-C5-C6) angles were edited from 111 to 100 degrees. These manipulations brought the reactive chain ends within a much greater proximity of each other so when the opt+freq calculation was run, optimising to a transtion state (QST2 this time, Hartree-Foch/3-21G), the result was a boat transition state.
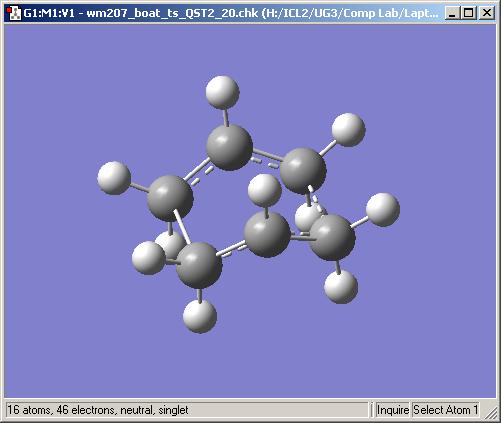
The Intrinsic Reaction Coordinate (IRC)
The boat transition structure was created using an optimised anti2 hexadiene, but by the time it had been manipulated to react more readily it was closer in appearance to one of the higher energy gauche conformations. On the other hand, the chair transition state was created using allyl fragments which bear little in relation to hexadiene chains. Knowing which conformer is most closely related to each transition state would be useful in determining which one the Cope Rearrangement is most likely to use.
IRC is a method which makes small changes in geometry towards the direction which has the steepest energy gradient. In this way it follows the reaction away from the transition state towards the nearest hexadiene conformer whilst maintaining a relatively optimised moleculur structure at each step.
The optimised chair transition structure was subjected to IRC analysis, because the reaction coordinate is symmetrical it was only necessary to follow the reaction forwards and the calculation was instructed to take 50 steps from the transition state. The result showed 26 optimised steps away from the transition state and it was quite obvious that the final step was not a lowest energy conformer. In fact the IRC plot shows that the RMS gradient has not reached zero by the end of the calculation and this is the first sign that the calculation has not reached a minimum.
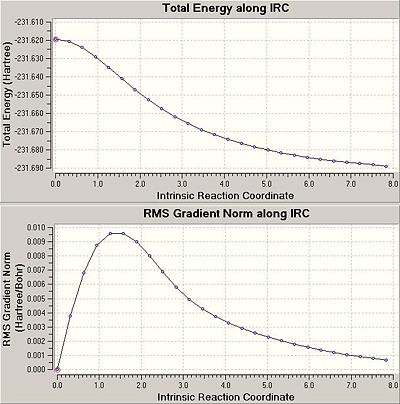
The options to reach a minimum were to simply take the final product of the IRC calculation and subject it to a normal minimization calculation, to re-run the IRC but this time with a greater number of points or to re-run the IRC calculating the force constants at every step. The first option is quickest and most straightforward, the second option requires more computing resources but offers slightly greater fidelity, the third option is most reliable for finding the correct minimum but requires a lot more computational resources.
The quickest option was used first, as it would quickly determine its usefulness, and returned a very agreeable optimised molecule which was identified as gauche2. The second option was then employed to verify the results of the first although increasing the number of steps first to 60 and then to 75 did not reach minima. The third option was not used due to time constraints.
Transition State Activation Energies
The Chair and Boat transition structures optimised earlier were optimised with a fairly low level basis set, optimising with a slightly higher level basis set means the results can be compared with experimental data more reliably. As the anti2 hexadiene is the lowest energy conformer that will be the basis for calculating activation energies and it has already been optimised at the DFT/B3LYP/6-31G* level so it followed to optimise the chair and boat transition structures at the same level (it has been noted already that it is only possible to compare calculations run at the same level of accuracy).
The geometries of the re-optimised molecules were virtually indistinguishable from the originals, however the energies changed markedly:
| Total Electronic Energy | Sum of electronic and Zero point energies |
Thermal energies | Thermal enthalpies | Thermal free energies | |
|---|---|---|---|---|---|
| Chair HF/3-21G | -231.6192 | -231.4667 | -231.4613 | -231.4604 | -231.4952 |
| Chair DFT/B3LYP/6-31G* | -234.5675 | -234.4149 | -234.4090 | -234.4081 | -234.4438 |
| Boat HF/3-21G | -231.6028 | -231.4509 | -231.4453 | -231.4444 | -231.4798 |
| Boat DFT/B3LYP/6-31G* | -234.5431 | -234.4023 | -234.3960 | -234.3951 | -234.4318 |
| anti2 HF/3-21G | -231.6925 | -231.5395 | -231.5326 | -231.5316 | -231.5709 |
| anti2 DFT/B3LYP/6-31G* | -234.6117 | -234.4692 | -234.4619 | -234.4609 | -234.5008 |
The activation energies were calculated as the difference between the energies of the ground state molecule (anti2 hexadiene) and the transition states, scaled to kcal/mol in order to compare with the experimental values.
| T=0K | T=298K | expt T=0K | |
|---|---|---|---|
| Chair HF/3-21G | 45.71 | 44.70 | 33.5 ± 0.5 |
| Chair DFT/B3LYP/6-31G* | 27.15 | 26.29 | |
| Boat HF/3-21G | 55.60 | 54.76 | 44.7 ± 2.0 |
| Boat DFT/B3LYP/6-31G* | 41.96 | 41.32 |
The calculated activation energies, when compared to experimental values seem a bit vague as they manage to have bracketed the experimental result but it can be noted that at the higher level basis-set the numbers are much closer to the correct answer. Also the boat is much higher in ernegy than the chair which is what one would expect.
The Diels-Alder Cycloaddition
Cis-butadiene and Ethene

The Diels Alder Cycloaddition is a pericyclic [4s+2s] reaction in which a diene reacts with a dieneophile. The simplest example of this reaction occurrs between ethene and butadiene. These molecules have different symmetry for their HOMO and LUMO orbitals which means the HOMO of one overlaps very well with the LUMO of the other allowing the reaction to proceed in a concerted fashion. This can be seen in the MO images below:
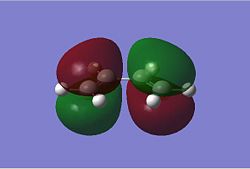 |
 |
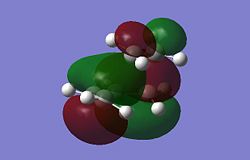 |
 |
 |
 |

The table above contains the MOs in rows that are subsequently mixed to form the MOs of the transition state. It is important to note that their symmetry is different with respect to the plane indicated in the picture on the right, they can either be symmetric (s) or asymmetric (a). The symmetry has been listed in a table below for convenience.
| Cis-butadiene | Ethene | |
|---|---|---|
| HOMO | a | s |
| LUMO | s | a |
As it has already been hinted at above the transition state was successfully calculated using the TS Berny method detailed earlier. The particular appeal of this method was that the manual editing is fairly straightforwards and once done the optimisation is fast and rarely returns errors. The ethene molecule was manipulated into a rough position above the open end of the diene (note the ethene molecule has to add to one face of the diene and cannot be in the same plane) approximately half-way between the double-bonds, most importantly the distance between the atoms forming new bonds was edited to approximately 2.2 angstroms. (This calculation was run at the HF/3-21G level) The result was verified by the presence of one imaginary frequency at -818.29cm-1 corresponding to the Diels-Alder reaction:
 |
 |
It is noteworthy that the imaginary vibration is a synchronous vibration which shows that the reaction definitely would proceed in a concerted fashion. Although the displacement vector arrows on the image above are pointing away from where the new bonds should form the atoms vibrate both towards and away from each other and the fact that both sets of arrows point in the same direction is evidence of a synchronous vibration.
Regioselectivity
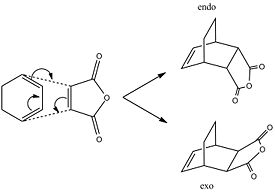
In order to examine the regioselectivity of the Diels Alder reaction it is necessary to look at a more complicated example, that of cyclohexadiene and maleic anhydride.
