Rep:Module3:mr60712789

Computational Chemistry Lab- Module 3: Physical

In this module computational chemistry will be used to model transition states on potentail energy surfaces for the Cope rearrangement and Diels Alder Cycloaddition reactions. The method of computational analysis used in module 1 is not able to be implemented in this investigation because the method does not involve the breaking and formation of bonds, which is what occurs in the formation of a transition state. The method that will be used in this section of the computational labs will implement molecular orbital methods in which the Schrodinger equation and locating transition states based on the potential energy surface. Furthermore barrier heights, reaction pathways and transition states structures will be investigated.

The Cope Rearrangement

Cope Rearrangement

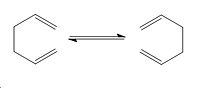
The Cope Rearrangement is a [3,3]-Sigmatropic Shift and occurs in a concerted fashion via a chair or a boat transition state. The overall aim of this investigation is to locate the low-energy minima and the transition state structures of the C₆H₁₀ molecule, by optimising and anlaysing both the products, reactants, and transitions states.

Optimising the reactants and products

	Anti Conformer
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
C1-C4 Dihedral Angle/o	176.9
Total Energy/a.u.	-231.69260
RMS Gradient/a.u.	0.000019
Dipole Moment/D	0.202
Point group	C2

The molecule was drawn in ChemBio3D and imported into Gauss View. In drawing the molecule it was ensured that the carbon structures were drawn anti-periplanar to each other (i.e. with an "anti" linkage). This was done in ChemBio by setting the dihedral angle to 180^o. Once imported into GaussView the structure was "cleaned" and then optimised using the HF/3-21G method and basis set respectively. The optimisation took 58 seconds to run and produced the following results shown to the right. It can be seen from comparison to Appendix 1 that the anti conformer produced by the optimisation is anti 1. This is because the energies are the same and that their point groups (symmetry) is aswell. It should be noted that the point group above was the point group given in the "summary", and when "Symmetrize" was selected the point group was found to be the same at C₂.

	Gauche Conformer
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
C1-C4 Dihedral Angle/o	-71.1
Total Energy/a.u.	-231.68962
RMS Gradient/a.u.	0.000015
Dipole Moment/D	0.444
Point group	C1

A gauche version of the 1,5-hexadiene was drawn in ChemBio, ensuring that the dihedral angle was set to 60^o and imported to GaussView. The molecule was optimised in the same fashion as above using the same basis set and method as in the above anti molecule (HF/3-21G). The reaction took 1 minute and 34 seconds and produced the results shown to the left. It can be seen, in comparison to the appendix, that the gauche confromer that was produced by the optimisation was the gauche 5 molecule, which has the same symmetry and energy as my optimised molecule. It should be noted that, similar to above, the point group after selecting "symmetrzie" was found to be C₁. The energy of this gauche conformer was found to be very similar to that of the anit conformer, however the anti was slightly lower in energy with a difference of 7.82kJ. It can be seen from the results above that an anti conformer is going to be more stable: it has the lower dipole and the dihedral angle of 180 ^o and will enable the bonds to be least hindered. However a small degree of gauche character will be needed to make the molecule more entropically favoured, because an anti structure is too rigid which is entropically unfavoured. Using this theory it can be assumed that the lowest energy molecule will be Anti with Gauche character (which is the same as Gauche with an Anti character). This molecule was generated in ChemBio by drawing the gauche structure, and then altering the dihedral angle from the optimum of 60 to 70 degrees. This molecule was optimised, taking 1 minutes and 10 seconds and yeidling the following results:

	Gauche Conformer with Anti Character
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
C1-C4 Dihedral Angle/o	67.7
Total Energy/a.u.	-231.69266
RMS Gradient/a.u.	0.000003
Dipole Moment/D	0.3406
Point group	C1

From this it can be seen, with repect to the appendix, that the conformer generated with this optimisation is gauche 3 as it is of the same energy and symmetry (point group). This is the conformer which is lowest in energy and therefore is the most stable. The C_i anti2 conformer of 1,5-hexadiene was drawn in ChemBio, inserted into GaussView and optimised using the HF/3-21G to ensure that C_i symmetry was present. This yielded the following results:

	Anti to get Ci
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
C1-C4 Dihedral Angle/o	180
Total Energy/a.u.	-231.69250
RMS Gradient/a.u.	0.00001
Dipole Moment/D	0.0005
Point group	C1

	Reoptimised ci
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d)
Charge	0
Spin	Singlet
C1-C4 Dihedral Angle/o	180
Total Energy/a.u.	-234.61171
RMS Gradient/a.u.	0.000014
Dipole Moment/D	0.0005
Point group	C1

It can be seen here that the optimised geometry was found to be C₁, however upon selecting "symmetrize" it was found to be C_i. This is further confirmed by the dihedral angle which was found to be 180^o, thus proving the molecule can have a centre of inversion. This output file was then further reoptimised using the DFT method and selecting the B3LYP, and using the basis set of 6-31G*. This resulted in the following data: It can be seen that the more accurate basis set of 6-31G* has optimised the molecule further to produce a lower energy of -234.61171a.u., which is a decrease in energy of 7664.39kJ. This means that the reoptimised molecule is far more stable than the one generated with the less accurate and less complex basis set. It is also important to note, similarly to the above initial optimsiation of the anti2 molecule, in the summary table shown to the right, the symmetry point group was found to be C₁. However, again similar to the initial optimisation, upon selecting "Symmetrize" and selecting the point group, the point group was found to be C_i. This is logical because the dihedral angle is found to be 180^o which is necessary for a centre of inversion. Using the file created from the reoptimisation of C_i, the frequency analysis was run using the same method (B3LYP) and basis set (6-31G*), selecting "frequency". The reaction took 2 minutes and 21 seconds and yielded the following results :

IR Spectrum of 1,5-Hexadiene

Mode Number	Frequency/cm-1	Intensity		Description
9	670	20.0	Mode9	Rocking Stretch
10	788	4.0	Mode10	Rocking Stretch
11	938	12.8	Mode11	Twisting Stretch
13	940	60.9	Mode12	Rocking Stretch
17	1036	19.7	Mode17	Twisting Stretch
19	1068	9.6	Mode19	Scissoring Stretch
22	1289	6.5	Mode22	Rocking Stretch
30	1524	5.6	Mode30	Scissoring Stretch
32	1734	18.1	Mode32	Asymmetric Stretch
34	3032	53.6	Mode34	Symmetrical Stretch
36	3080	56.2	Mode36	Asymmetric Stretch
39	3155	14.7	Mode39	Symmetrical Stretch
42	3234	45.4	Mode42	Asymmetric Stretch

The results table shows the major vibrations within the molecule. It should also be noted that there are 18 zero intensity frequencies all generated by vibrations which cause no net change in the dipole moment and thus are IR inactive. The frequency analysis was analysed to ensure that a global minima had been generated in the optimisation. The file was found to have no negative (imaginary) frequencies, and therefore a global minima had been reached. The thermodynamic data produced by the analysis was shown below:

The sum of electronic and zero-point energies: -234.46920 a.u. The sum of electronic and thermal energies: -234.46186 a.u. The sum of electronic and thermal enthalpies: -234.46091 a.u. The sum of the electronic and thermal free energies: -234.50078 a.u.

These values correspond to the potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE), the energy at 298.15 K and 1 atm of pressure including contributions from the translational, rotational, and vibrational energy modes (E = E + Evib + Erot + Etrans), an additional correction for RT (H = E + RT) , and the entropic contribution to the free energy (G = H - TS) respectively.

Optimising the chair and boat transition structures

Optimised CH₂CHCH₂ Inital Fragment

In this section the boat and the chair transition state structures were optimised using 3 different methods: by computing the force constants, using the redundant coordintate editor, and using QST2. The reaction coordinate can then be generated, an IRC will be run and the activation energies of the Cope Rearrangement for the "chair" and "boat" transition states will be generated. As the chair and boat transition states consist of C₃H₅ allyl fragments in close proximity, with differing symmetries of C_2h and C_2v, initially a CH2CHCH2 allyl fragment will be optimised using the HF/3-21G method and basis set. This optimised fragment will be used in the further calculations.

Chair

Initial Guess for Transition State Structure

The optimised fragment generated in the optimisation above was copied and pasted twice into the same window. The 2 fragments were orientated to ensure that they were 2.2A apart at the ends of each of the fragments. This molecule is the "initial guess" at the structure of the chair transition state. This initial guess structure was optimised using 2 different methods. It is important to note that optimisations of transition states are more complex than normal optimisations because the negative direction of curvature is needed to be known. The first optimisation was done by generating an initial structure that was close to the actual structure of the transition state. A downside of this is that the inital guess has to be similar to the actual structure because otherwise the potential surface will be greatly different to that of the actual transition state. The inital molecule was optimised by selecting optimisation+frequency, using the HF/3-21G method and basis set, with the optimisation set to a transition state (Berny). "Opt=NoEigen" was filled into the additional keywords section to ensure that only 1 negative curvature was generated during the optimisation. This is known as the Force Constant Method. The second optimisation method was optimisation carried out by setting the coordinates of the transitions state and stopping them from moving whilst still allowing the rest of the molecule to move. The inital guess structure was the same as the structure above. Once the molecule has been optimised holding some of the transition state points in set places, the molecule is optimised for a second time in which the points are not frozen. This second optimisation generates the transition state. This method was known as the Redundant Coordinate Editor Method. It must be noted that in this analysis imaginary frequencies are generated. These frequencies arise because the mode of vibration found in the molecule is what is happening in the reaction pathway as the transition state forms the product.

The force constant method took 32 seconds and the redundant coordinate method took 25 seconds for the first optimisation and 28 seconds for the second optimisation .

	Force Constant Method	Redundant Coordinate Method
Calculation Type	FREQ	FREQ
Calculation Method	RHF	RHF
Basis Set	3-21G	3-21G
Charge	0	0
Spin	Singlet	Singlet
Total Energy/a.u.	-231.6193224	-231.6193225
Total Energy/kJ	-608116.531	-608116.5312
RMS Gradient	0.00003141	0.00003141
Dipole Moment	0.0002	0.0002
Imaginary Frequency	1	1
Point Group	C1	C1
Distance to form/break bond /A	2.02055	-2.02053
Imaginary Frequency/cm-1	-818.05	-818.05
Time Taken To Run	32 seconds	28 seconds

It can be seen that both methods produced the same energies, dipole moments and distances between the 2 ends of the fragments. It can also be seen that upon inspection of the transition states generated and analysis of the 2 imaginary frequencies, that the molecules generated are identical. This calculation can show that the first method of using the force constant analysis is suitable for this calculation and that the second method, which invlovles 2 optimisations and so takes longer to produce the same results, does not need to be done. From this analysis the Force Constant Method is what will be implemented in the analysis of the Diels-Alder Reaction below.

Boat

Numbered Reactant

Numbered Product

The Boat conformer was optimised using the QST2 method. This method works by specifying the reactant and product structures, and works out the transition state structures by calculating the potentail energy surfaces and going through them to work out which is the best approximation for the transition state structure. The analysis was carried out on the optimised anti2 structure generated in earlier analysis. The molecule was pasted into 2 separate windows to generate both the product and the reactant molecules. These were numbered differently to ensure that the product was numbered to be consistent with the reaction. An Opt+freq calculation was run using the TS(QST2). It was discovered that an error report was generated.

Upon closer inspection of the file it can be seen that the transition state looks like a chair with crossing connection bonds, and so the boat transition state has not been generated. This is to do with how the method works: the programme works by translating the product and not including rotation around bonds. Therefore it can be seen that, in order to get the correct boat transition state, rotation around bonds is required. In order to get the optimisation to work, the product and the reactant are rotated so that their geometry is approximately the same and will produce the correct geometry of the transition state. The molecule was rearranged so that the C-C-C-C dihedral angle was set to 0^o and that the internal C-C-C angles were set to 100^o for both the reactants and the products, generating the image to the left. The molecules were optimised in this way to ensure that the initial product and reactant structures are similar in shape to the transition state. This was optimised yielding the following results:

Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy/a.u.	-231.60280
Total Energy/kJ	-608073.1577
RMS Gradient	0.000022
Dipole Moment	0.1585
Imaginary Frequency	1
Point Group	CS
Distance to form/break bond /A	2.1397
Imaginary Frequency/cm-1	-840
Time Taken To Run	22 seconds

It can be seen from the frequency analysis that the minima produced was a global minima because only 1 negative frequency was generated, which corresponded to the Cope Rearrangment itself, thus confirming that the molecule was fully optimised and the optimisation was a success. The following thermochemical data (in atomic units) was produced:

Sum of electronic and zero-point Energies= -231.4509

Sum of electronic and thermal Energies= -231.4453

Sum of electronic and thermal Enthalpies= -231.4443

Sum of electronic and thermal Free Energies= -231.4798

It can be seen, in comparison to the chair conformer, that the energy of the boat is slightly higher than the energy of the chair. This is expected because of the increase in the steric strain of the boat conformation compared to the chair. By inspecting the molecule the original conformer which underwent the reaction can't be determined. Therefore a further optimisation method was used: The Intrinsic Reaction Coordinate (IRC). This calculation method works by creating a series of small geometry steps in which the slope of the energy surface is steepest. This will enable the conformer which was used in the reaction to be calculated because every step of the reaction can be followed. The IRC calculation was carried out on an optimised chair transition state generated in an earlier optimisation. The reaction coordinate was calculated in the forward direction because of the symmetry of the reaction. The number of IRC steps was set to 50 to ensure that there were enough steps to complete the calculation. Force constants were only calculated for the beginning of the calculation by selecting "once". The reaction took 1 minute 55 seconds to run. The IRC took 16 steps and so not all of the 50 steps set were required. It can be seen from the output file that the molecule was not completely optimised (the gradient of the graph has not levelled off suggesting that a minimum has not been reached), thus the molecule has reached a local minima and not a global minia. As a result one of 3 further methods could have been used to complete the optimisation. These were: run an optimisation on the end result of the IRC, to run a second IRC from the end result of the first IRC, or to redo the IRC whilst specifying that the force constants were to be computed all the way through the optimisation. The downside of option one is that if the local minima is not close to the global minima then the global minima may not be reached. The downside to option 2 is that it is a time consuming process and may still give the wrong structure. As a result option 3 was run, taking 29 minutes and 42 seconds(51 steps)and yielding the following results.

From this it can be seen that a minimum has been reached because the graph plateaus off, unlike in the first IRC calculation. The bond length needed in the formation/breaking was found to be 1.696Å.

Comparison of Boat and Chair Activation Energies

The chair and boat transition states were optimised to a higher method and basis set (DFT, B3LYP and 6-31G*) by optimising the originally optimised boat and chair files produced earlier. The results are shown below:

	1,5-Hexadiene (anti2)		Chair Transition State		Boat Transition State
	HF/3-21G	B3LYP/6-31G*	HF/3-21G	B3LYP/6-31G8	HF/3-21G	B3LYP/6-31G8
Sum of Electronic and Zero-Point Energies at 0K	-231.540	-234.469	-231.467	-234.415	-231.451	-234.402
Sum of Electronic and Zero-Point Energies at 298.15K	-231.533	-234.462	-231.461	-234.409	-231.445	-234.396
Total Electronic Energy	-231.692	-234.612	-231.619	-234.557	-231.603	-234.543

The activation energies were calculated by subtracting the transition state sum of electronic and zero-point energies from the sum of the electronic and zero-point energies of the starting 1,5-hexadiene. This difference was then multiplied by 627.509391 to convert from atomic units to kcal/mol This yielded the following results:

	Chair TS		Boat TS
	ΔE at 0K (kcal/mol)	ΔE at298.15K (kcal/mol)	ΔE at 0K (kcal/mol)	ΔE at298.15K (kcal/mol)
HF/3-21G	45.808	45.181	55.848	55.221
B3LYP/6-31G8	33.886	33.258	42.043	41.416
Experimental	33.500	-	44.700	-

When the results are compared with the data in appendix 2 it can be seen that the energies are in good agreement because they are identical. This is to be expected because they are generated using the same methods and basis sets. The comparison between the obtained results for activation energy and the activation energies given in the appendix show that these are in good agreement, again as they were produced using the same method. It can also be seen tht the experimental values are in good agreement with the calculated computational values with small deviations (smaller as the complexity of the basis set is increased), likely to be because the experimental method for calculating activation energies is likely to be less accurate than that of the computational method. From the results obtained it can be seen that the chair transition state is lower in energu and has a lower activation energy than the boat transition state. This is likely to be due to the extra strain present in the boat conformer, and as a result the Cope Rearrangement will proceed via the chair conformer as the reaction is kinetically controlled.

Conclusion

Overall it can be seen that various methods can be used to optimise geometries of a molecule. Furthermore it can be seen that more complex methods have to be used when attempting to optimise a transition state. It can be concluded that the Cope Rearrangement, whilst kinetically controlled, will reach the product via a chair transition state because it has a lower activation energy.

Diels-Alder Cycloaddition

In this section of the investigation the Diels-Alder Reaction between ethylene and butadiene will be computationally analysed. The Diels-Alder reaction is a [4s+2s] Cycloaddition which occurs between a dienophile (ethylene) and the diene (butadiene). The pi orbital of the dienophile forms a sigma bond with the pi orbital of the diene. It is important to note that in this Diels-Alder Cycloaddition 2 sigma bonds are formed (and at the same time 2 anti bonding orbitals).The reaction is concerted and stereospecific. Therefore, depending on the electron count used, it can be either allowed or forbidden.

The Reaction Scheme for the Diels Alder Reaction of Ethylene and Butadiene

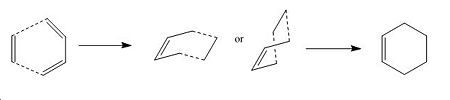
The reaction occurs when there is large orbital overlap between the diene and the dienophile. The aim of this section is to characterise the transition state using one of the methods previously used in the Cope Rearrangment Section. The orbitals involved will be generated and discussed, the tranition state will be optimised and analysed, and the regioselectivity of the molecule will be investigated.

MO Diagrams for Ethylene and Butadiene

MO Diagram for Ethylene

MO Diagram for Butadiene

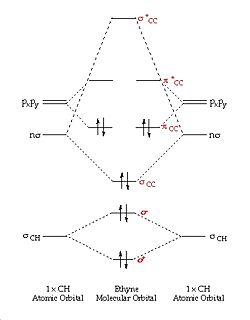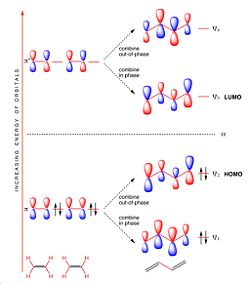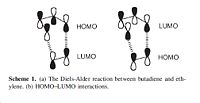
The main interaction in this reaction is the π/π* orbitals of the ethylene and the HOMO/LUMO of butadiene. It can be seen from the MO diagrams below that there are 2 degenerate filled orbitals that make up the HOMO in the ethylene, and it can be seen that there is only 1 oribtal making up the HOMO for butadiene. This is why the reaction is 4s+2s, the ethylene contributes 4 electrons and the butadiene contributes 2 electrons. Both the HOMO of ethylene and the LUMO of butadiene are symmetric with respect to the reflection plane (denoted s) and the HOMO of butadiene and the LUMO of ethylene are antisymmetric with respect to the plane of rotations (denoted a). Therefore both the HOMO and LUMOs of ethylene and butadiene can interact because they are of the correct symmetry. This interaction between the HOMO/LUMO pairs means that the HOMO of the generated Diels-Alder Product will have 2 new sigma bonds which will be a.

cis-Butadiene

Initial Optimisation of cis-Butadiene

AM1 Optimisation of cis-Butadiene

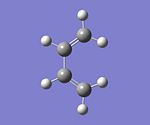
Cis butadiene was drawn in ChemBio3D and imported into Gauss View. The molecule was cleaned using the "edit-Clean" function, and initially optimised using the HF/3-21G method and basis set to ensre that further calculations ran faster. The optimised product is shown to the left. This optimised structure was reoptimised using the AM1 semi-empirical molecular orbital method, in order to generate the HOMO and the LUMO for cis-butadiene and determine the symmetry of the molecule with respect to the plane (whether the molecule was a or s). From analysis of the more optimised molecule (shown right) both are planar with a dihedral angle of 0^o. Furthermore the AM1 optimisation has an increase in C-C-C bond angles, from 125.67^o in the initially optimised molecule to 126.65^o in the AM1 optimised molecule. The MOs (HOMO and LUMO) generated are shown below:

HOMO and LUMO of cis-Butadiene

HOMO	LUMO
HOMO of cis-Butadiene	LUMO of cis-Butadiene

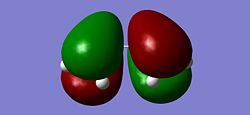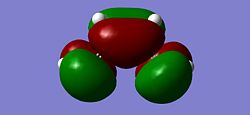The energy of the HOMO was found to be -0.34381a.u. and the energy of the LUMO was found to be 0.01797a.u. leading to a HOMO/LUMO gap of 947.49kJ, a large energy gap. It can be seen that the HOMO has 1 nodal plane. This is consistent with the MO diagram shown above which shows the combination of 2 in-phase p orbitals with 2 p orbtials which are of a different phase, thus generating a nodal plane. Therefore it can be deduced that the HOMO is antisymmetric with respect to the reflection plane (a). It can be seen that th LUMO has 2 nodal planes. Again this is consistent with the MO diagram which shows the LCAO of 2 in-phase p orbitals in the centre of the molecule and 2 out of phase p orbitals on either side, generating 2 nodal planes. The LUMO is therefore symmetrical with respect to the reflection plane (s). This confirms what is said above, that the HOMO and the LUMO of cis-Butadiene are of differing symmetries and so reaction the reaction occurs between the HOMO and LUMO in ethylene and butadiene.

Transition State of Cycloaddition of Ethylene and cis-Butadiene

As can be seen in the image, the transition state is said to have an "envelope" shape. This will enable maximum overlap of the atomic orbtials. The transition state conformation was obtained by assuming the starting geometry to be that of a bicyclic with the bridged fragement removed. The interfragment lines were guessed to be 1.6A becuase it is slightly longer than an average C-C single bond, the type of bond that will be generated in the reaction. The optimisation method that will be used is the Force Constant Matrix because a rough idea of what the transition state looks like has been found. The Frozen Reaction Coordinate Method was not chosen because the bond length between the terminal carbons is not known, and despite a guess of approximately 1.6A being made, it is likely that the calculation will not work if the guessed bond distance is not close to that of the actual bond distance. The transition state was drawn in ChemBio and imported into GaussView. An initial optimisation using the HF/3-21G method and basis set was used to basically optimise the molecule. The generated molecule, shown to the right was then reoptimised selecting AM1 and optimising to a TS(Berny). The distance between the butadiene and ethylene was decided to be 2.15A . This distance should enable a transition state structure to be generated. If the bond distance was smaller, the optimisation will just yield the product, any larger and a transition state will not be generated. The calculation yielded the following results:

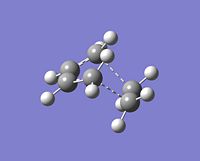	HOMO of Transition State	LUMO of Transition State

It can be seen that the butadiene character is still maintained, with 2 of the bonds which were originally double bonds having a bond length of 1.38A in the transition state. Furthermore the C(H)-C(H) bond between them, originally a single bond, has a slightly longer length of 1.40A. The ethylene fragment, originally having a double bond, has a bond length of 1.38A. This shows that the double bonds in the starting reactants increase in bond length to form a bond of 1.38A in the transtion state, which is between the literature values of a single and carbon double bond (1.54A and 1.34A respectively). This suggests that the double bonds are becoming single bonds in character, consistent with a Diels-Alder reaction. The 2 new sigma bonds that are forming have a length of 2.12A and the Van der Waals radius of carbon is 1.7A. The optimum Carbon sp² bond length is 1.30A and the optimum sp³ bond length is 1.54 A , and this, along with the Van der Waals radius of carbon, suggests that there is strong interactions between the nuclei of the atoms forming the bonds. Furthermore it can be seen that the bond is mainly sp² in character but heading towards sp³ in character, fitting with the Diels-Alder Reaction.

Orbital in the Transition State

Reaction Vibration

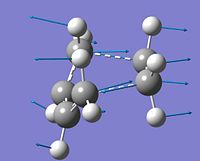
From the HOMO and LUMO generated it can be seen that the HOMO is asymmetric (a) and that the LUMO is symmetric(s). The HOMO is generated from the pi* orbital of the ethylene fragment and the HOMO of the butadiene molecule, both antisymmetric, (shown in the MO diagram above) and combine to form the HOMO Orbital generated. The LUMO is generated from the HOMO of the ethylene and the LUMO of the butadiene (both symmetric). The Orbitals involved in the transition state is shown in the image to the left. To check that the reaction had reached a global minima and not a local minima, the vibrations of the molecule were checked. It can be seen that only 1 negative frequency was generated, and this corresponded to the reaction. This frequency occured at -956cm^-1 and shows the concerted formation of the 2 new sigma bonds. The lowest vibration after the imaginary frequency corresponds to the twisting vibration of the ethene molecule within the transition state formation. This could lead to a non concerted bond formation.

A Study of the Regioselectivity of the Diels-Alder Reaction

The Diels-Alder Reaction of Maleic Anhydride and Cyclohexa-1,3-diene has 2 possible stereochemical outcomes: an exo and an endo product.

Regioselectivity of Diels Alder Reaction of Maleic Anhydride and Cyclohexa-1,3-diene

A rough image of both the exo and endo transition states were generated, based on literature structures of the transition state . An "Opt+Freq" calculation was run selecting force constants as "always", entering "Opt=NoEigen" into the additional words, "TS(Berny)" was selected to ensure a transition state was generated, and the semi-empirical AM1 method and basis set was selected. The frozen coordinate method was not chosen because the terminal bond lengths were not known. The calculations yielded the following results:

	HOMO of Exo Transition State (From Above)	HOMO of Exo Transition State (From Side)	LUMO of Exo Transition State (From Side)	LUMO of Exo Transition State (From Side)
	HOMO of Endo Transition State (From Above)	HOMO of Endo Transition State (From Side)	LUMO of Endo Transition State (From Side)	LUMO of Endo Transition State (From Side)

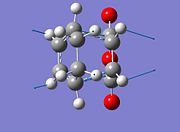
It can be seen from the MOs that the maleic anhydride C(O)-O-C(O) secondary orbital overlap with the C(H)=C(H) overlap is greater in the endo product than the exo product. This stabilises the endo product more than the stabilisation in the exo and thus decreases the total energy of the molecule (for energies see below). There is greater secondary orbital overlap on the endo becuase the 2 fragments are on the same face and so are better aligned, thus increasing the overlap in comparison to the exo. Furthermore the 2 pi bonds are on 1 face in the endo molecule, but in the exo they are not on the same face and this decreases the overlap making the exo higher in enegy. It can be seen from the MOs that both the endo and the exo have a nodal plane down the plane symmetry. Furthermore it can be seen that in the endo there is a small amount of electron density on the oxygen atom, which is in the same phase as the secondary orbital overlap which will lead to a greater interaction, thus stabilibising the endo product further. The presence of the 3 oxygens (2 carbonyls and a bridging O) mean that the mealeic anhydride is strongly electron withdrawing, and so will favour donation into the LUMO over donation from the molecule's HOMO. Therefore the interaction in the formation of the new bond is between the LUMO of the maleic anhydride and the HOMO of the cylohexandiene to produce the strongest bond in the transition state.

	Endo	Exo
Sum of electronic and zero-point Energies	0.133494	0.134881
Sum of electronic and thermal Energies	0.143683	0.144882
Sum of electronic and thermal Enthalpies	0.144628	0.145826
Sum of electronic and thermal Free Energies	0.09735	0.099118
Bond Length of Newly Formed σ bonds/A	2.16	2.17
Transition State Total Energy/a.u.	-0.0515	-0.0504
Dipole Moment/D	6.1662	5.56
RMS Gradient/a.u.	0.00000102	0.00000112

It can be seen that the endo transition state is lower in energy than the exo product with a difference of 2.89kJ between them. This is likely to have been caused by the increase in steric clash between the endo and exo forms and the secondary orbital overlap (explained above). In the exo form there is a large degree of steric clash because the the maleic anhydride has a large bulky 3 oxygen group which is on the same side as the the briding carbon thus generating a large steric clash. In contrast in the endo transition state the bridge is on the opposite side to the bulky anhydride and therefore the only clash is between the hydrogens and the group. This increase in clash in the exo molecule is reflected in the bond length of the newly formed sigma bond, which is larger in the exo than in the endo. The higher energy is also due to the endo molecule having a smaller RMS gradient and therefore is closer to the desired bond angles and lengths which each atom in the molecule would like to be at.

Endo	Exo
-812cm-1	-806cm-1

It can be seen that these negative imaginary vibrations correspond to the reaction occuring to take the reactants to the products via the transition state. The generation of the one negative frequency shows that the optimisation has reached a global minima and not a local minima. Therefore the opimisation has been successful.

Conclusion

Overall it can be seen that many methods can be used to model transition states. Furthermore the Diels-Alder Reaction is stereospecifically controlled, with the production of the more stable endo product being energetically favoured over the exo product.