Rep:Module3:JYX08
The Cope Rearrangement
The Cope Rearrangement of 1, 5-hexadiene, originally developed by Arthur C. Cope, which specifically involves a [3, 3] sigmatropic shift rearrangement of 1,5-dienes. Although it has been heavily debated whether the mechanism of Cope Rearrangement goes via a concerted, stepwise (two-stage diradical intermediate) or dissociative, but now it is accepted that the rearrangement occurs in a concerted fashion via the either the chair or the boat configuration. In this section of the reportGaussian[1] will be used with Hartree-Fock (HF) and density functional theory (DFT)[2] methods, to optimise the structures of the transition states (TS), in order to locate the low energy transition states hence determine the most preferred mechanism for this reaction.
Optimisation of 1,5-hexadiene Conformers
The reactant 1,5-hexadiene can be considered to be in either "gauche" or "anti-periplaner" arrangements based on rotations around the central four carbon atoms. Due to the 6 carbon back bone, multiple Gauche and anti configurations can arise as reported by Gung and co-workers [3] that there are twenty seven theoretical conformations. However the symmetry of 1,5-hexadiene and the enantiomerism of the conformations left only 10 possible energetically distinct conformers. Different gauche and anti-periplanar conformers can be modelled by rotating the dihedral angles created by the alkene units and the central two carbon atoms. Molecules were drawn in Gaussview and each was "cleaned" and then "optimised" by Gaussian at Hartree-Fock(HF)/3-11G level of theory.
The table below shows examples of the optimised structures of the conformers, each with an associated total energy and point group:
| Conformer | Structure | Point Group | Energy/Hartrees | Relative Energy / kcal/mol | Log File | |||
|---|---|---|---|---|---|---|---|---|
| Anti1 |
|
C2 | -231.69260 | 0.04 | https://www.ch.ic.ac.uk/wiki/images/d/dc/JYX_anti1_OPT.LOG | |||
| Anti2 |
|
Ci | -231.69254 | 0.08 | https://www.ch.ic.ac.uk/wiki/images/b/bb/JYX_anti2_OPT.LOG | |||
| Anti3 |
|
C2h | -231.68907 | 2.25 | https://www.ch.ic.ac.uk/wiki/images/1/1a/JYX_anti3_OPT.LOG | |||
| Gauche2 |
|
C2 | -231.69166 | 0.62 | https://www.ch.ic.ac.uk/wiki/images/4/40/JYX_GAU2_OPT.LOG | |||
| Gauche4 |
|
C2 | -231.69153 | 0.71 | https://www.ch.ic.ac.uk/wiki/images/e/e1/JYX_GAU4_OPT.LOG |
Prediction of the Lowest Energy Conformer
My initial guess for the lower energy conformer was the anti- conformer, because the two alkene groups are further apart from each other when the central four carbon atoms are in anti-periplanar conformation. However the calculated results were infact opposite. "Gauche 3" conformer from Appendix 1 was shown to have the lowest energy. This result can be explained in terms of the Gauche effect. There exists favourable donation of electron density from the πC=C orbital of the C=C double bond into the σ*C-H orbital of the adjacent vinyl proton[4].
Further Optimisation of Anti 2 Conformer
The anti 2 conformer were optimised again using a higher level of theory of B3LYP/6-31G(d). Table below shows the comparison of the two calculations in terms of dihedral angle, bond length and total energy.
| Carbons used for measurement | Low level theory HF/3-21G | High level theory B3LYP/6-31G* | Difference |
|---|---|---|---|
| 1234 dihedral angle | 114.637° | 118.590° | 3.953° |
| 2345 dihedral angle | 180.0° | 180.0° | 0° |
| 3456 dihedral angle | 114.654° | 118.594° | 3.904° |
| 12 bond length/Å | 1.316 | 1.334 | 0.018 |
| 23 bond length/Å | 1.509 A | 1.504 A | 0.005 A |
| 34 bond length/Å | 1.553 | 1.548 | 0.005 |
| Total Energy/HF | -231.6925 | -234.6117 | 2.9192 |
The reoptimised molecule in terms of the bond length, did not change much, but in terms of the dihedral angle, there is a difference of 4°. The energy of the reoptimised structure was also decreased compare to the molecule optimised by lower level theory by 2.9 a.u.
Frequency Analysis
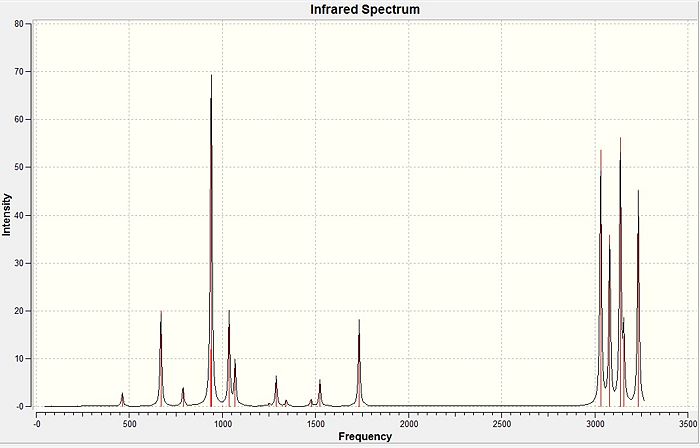
The reoptimised anti- conformer was then taken to run a frequency analysis with the same level of theory. This calculation will give the second derivative of the optimisation. This is useful as it can be used to check if we have indeed fully optimised the conformer. The frequencies must all be positive as this would indicate the minimum point on the energy curve. The frequency of the molecule was indeed all real and positive ranging from 73 cm-1 to 3233 cm-1.
Comparison of Energies at 0K and 298K
The table of values below are extracted from the Log file. Energies at 0K was recalculated by using the Freq=Readisotope option in Gaussian.
| Thermochemistry data from frequency analysis of 6-31G(d)-optimized 1,5-hexadiene | ||
|---|---|---|
| Analysis at 298.15K | Analysis at 0K | |
| Sum of electronic and zero-point energies / Eh | -234.46920 a.u. | -234.46877 a.u. |
| Sum of electronic and thermal energies / Eh | -234.46185 a.u. | -234.46143 a.u. |
| Sum of electronic and thermal enthalpies / Eh | -234.46091 a.u. | -234.46049 a.u. |
| Sum of electronic and free energies / Eh | -234.50077 a.u. | -234.50037 a.u. |
The total energy of the molecule becomes more negative as temperature increases. This is expected since the molecule absorbs more heat at higher temperatures, and thus thermal contribution to the energies increase.
Optimizing the "Chair" and "Boat" Transition Structures
Optimisation of Chair Transition State
The chair TS was optimised using HF/3-21G via two types of optimisation.
Opt 1: TS(Berny) Optimisation
Opt 2: A ModRedundant Minimisation with frozen C-C lengths, at 2.20 Å, for the C atoms involved in bond breaking/forming; followed by a TS(Berny) Optimisation with Hessian Derivative calculation for the C-C bond breaking/forming lengths
Optimisation of Chair Structure using TS(Berny)
A guessed chair TS structure was drawn on Gaussview using the optimised CH2CHCH2 structure as fragments. The distances in between the terminal carbon atoms in the two fragments were set to be 2.2 Å. The guessed strucuture was optimised to TS(Berny), and a frequency analysis was also done at the same time. The optimisation was set up so that the force constants were only calculated once with additional keywords, Opt=NoEigen, which prevents the calculation from crashing if more than one imaginary frequency is detected during the optimisation.

The frequency analysis shows that there is only one imaginary vibration at -817.85 cm-1.
It corrosponds to the bond forming and bond breaking of the [3,3]- sigmatropic rearrangement.
Optimisation of Chair Structure using Frozen Coordinates
In this method, the transition structure was generated by freezing the reaction coordinate of the terminal carbon atoms at the bond formation/cleavage positions, and then minimising the rest of the molecule using Opt=ModRedundant. Once the optimisation was done, the reaction coordinate was unfrozen and optimised to a transition state structure.
The table below shows a comparison between the two techniques:
| Properties | TS(Berny) | Frozen Coordinate |
|---|---|---|
| Final Energy / a.u. | -231.61933 | -231.61932 |
| Final Energy / kJ mol-1 | -608116.0 | -608116.5 |
| Imaginary Frequency / cm-1 | -817.85 | -818.21 |
| C-C Bond Breaking/Forming Length / Å | 2.02 | 2.02 |
As we can see from the table above, both technique gave very similar results, which means both methods are reliable enough for this calculation.
Boat Transition State Optimisation
The boat transition state was found using the QST2 method. The Ci anti 2 conformer was copied into a new window, and then pasted as "add molgroup". The reactant and product were then numbered corresponding to the reaction:
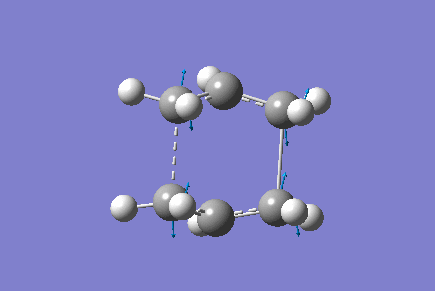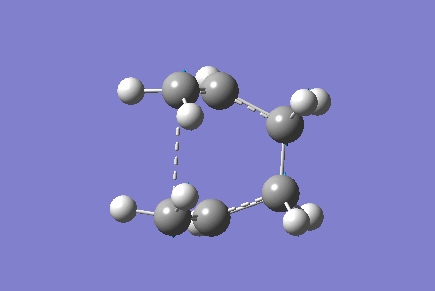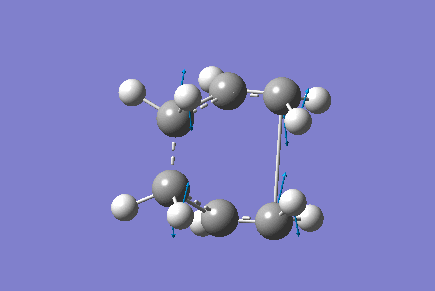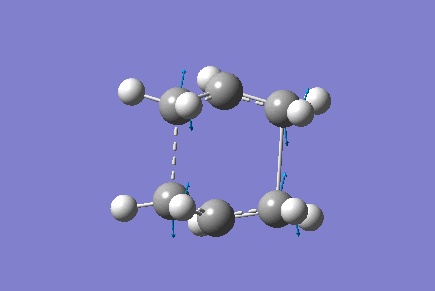
This was then sent to be optimised to a TS (QST2). The job failed to converge and so the reactant and product were altered manually so that they resemble the boat transition structure. The central C-C-C-C dihedral angle was changed to 0°, whilst the central C-C-C angles were changed to 100°. The TS (QST2) optimisation was then set up again.
The imgainary frequency was obtained at -840 cm-1
Optimised distance between the terminal ends of the allyl fragments was 2.13640 Å
Energy of transition state was -231.60280217 Hartrees
References
- ↑ Gaussian 09, Revision A.1, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian, Inc., Wallingford CT, 2009: web
- ↑ JP. Hohenberg, W. Kohn, Phys. Rev., 1964, 136, B864: DOI:10.1103/PhysRev.136.B864
- ↑ B. Gung and co-workers DOI:10.1021/ja00111a016
- ↑ B.G. Rocque, J.M. Gonzales, H.F. Schaefer III, Mol. Phys., 2002, 100, 441: DOI:10.1080/00268970110081412