Chemistry Computational Lab (Year 3)

Module 3: Transition States and Reactivity

Gaussview 5 & Gaussian09 was used in all modelling exercises.

The Cope Rearrangement

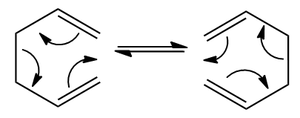
The proposed Cope rearrangement mechanism of 1,5-hexadiene is shown on the right. It has a cyclic transition state in between. To find the preferred reaction mechanism low energy minima and transition state structures must be considered.

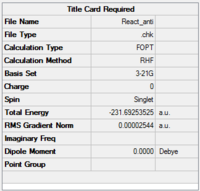
A molecule of 1,5-hexadiene with anti linkage at the centre 4 carbons was created and optimised under the conditions of HF/3-21G. This formation belongs to C_i point group. The energy was found to be the same as that of anti2 as stated in Appendix 1.

Another molecule of 1,5-hexadiene with gauche linkage was made and optimised with the methods same as above. The point group was found to be C₁. Comparing the results with Appendix 1, the structure is identified as gauche3.

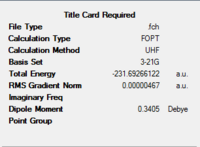
With direct comparison between the 2 conformers, gauche3 would be expected to be the less stable molecule due to steric hindrance between the double bonds. But the results show the opposite, with the energy for gauche3 (a.u.) is lower than that of anti1 (a.u.). This could be explained by the orbital overlaps at where the π orbital of C=C interacts with the σ* orbital of the adjacent C-H bond, which stabilises the gauche molecule.

We have to consider both sterically and stereoelectronically, as mentioned above, therefore gauche3 is expected to be the most stable conformer^[1]. Other conformers were produced and optimised to compare with each other.

*Table 1: Summary of the optimised gauche and anti structures of 1,5-hexadiene"*
Conformer	Energy (Hartree a.u.)	Point Group	D-space files
anti2	-231.69253525	C_i	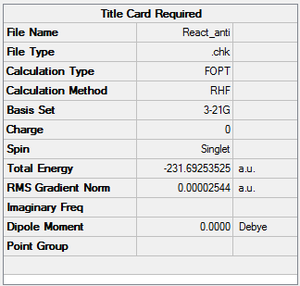DOI:10042/to-6275
gauche3	-231.69266122	C₁	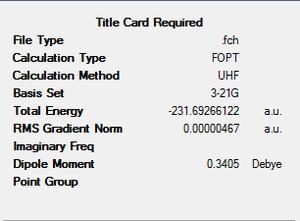DOI:10042/to-6273
anti1	-231.692260237	C₂	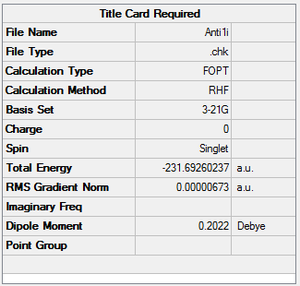DOI:10042/to-6277
gauche4	-231.69153533	C₂	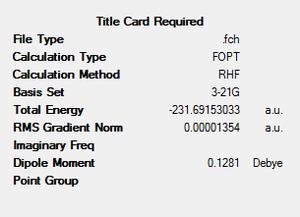DOI:10042/to-6272
gauche2	-231.69166702	C₂	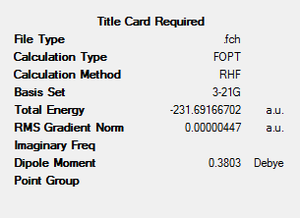DOI:10042/to-6271

The energies of different temperatures have very small differences So it is shown that the gauche3 possesses the lowest energy among all.

The C_i anti2 conformer was created and optimised (shown above) using the HF/3-21G method.

This molecule is then reoptimised with another basis set (DFT/B3LYP/6-31G*) which is a more accurate method. Comparisons are made between the 2 sets of results (3-21G and 6-21G*) in the table below.

*Table 2: Summary of the optimised anti2 structures of 1,5-hexadiene with different basis sets"*
Molecule
Basis set	HF/3-21G	B3LYP/6-31G*
File Type	.log	.log
Calculation Type	FOPT	FOPT
Calculation Method	RHF	RB3LYP
Final Energy / Hartree a.u.	-231.69253525	-234.55970425
RMS Gradient Norm / a.u.	0.00002544	0.00004599
Dipole Moment / Debye	0.000	0.000
Point Group	C₁	C₁

The geometry of the compounds have not changed much but there is a difference in energies of the two different calculation method. The 6-31G* method gives an energy which is lower by about 3 a.u. and a lower RMS Norm. This shows that the 6-31G is better at optimising compounds to lower energies. The table below shows the geometric data obtained from the 2 differently optimised compounds.

Table 3: Geometric properties of 2 differently optimised (anti2) 1,5-hexadiene
	Dihedral Angle (^o)			Bond Length (Å)
Basis set	C2-C3-C4-C5	C1-C2-C3-C4	C3-C4-C5-C6	C1-C2 & C5-C6	C2-C3 & C4-C5	C3-C4
'HF 3-21G	180.0	118.8	118.8	1.32	1.51	1.55
B3LYP 6-31G*	180.0	118.8	118.8	1.32	1.51	1.55

There is not a large difference between the geometric values two differently optimised compounds. Bond lengths differ by 0.01 Å at parts. Comparing with the lit. values (C=C 1.34Å, C-C 1.54Å, both simulations give good agreements.

Frequency analysis was carried out using the anti2 conformer, under 6-31G* optimisation. The IR spectrum of this compound is shown on the right.

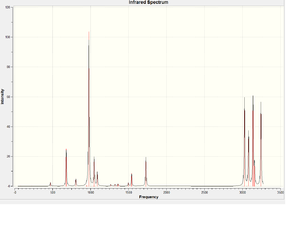
File on D-space: DOI:10042/to-6276 No imaginary frequencies were observed and this means it is optimised to its minimum.

Another analysis was carried out at 0K, and the results are shown below.

*Table 4: Thermochemical data from frequency analysis of optimised anti2 structures of 1,5-hexadiene with 6-31G* at different temperatures*
	298.15K	0K
Final Energies (E_h)	-234.559704	-234.559704
Sum of electronic and zero-point energies (E_h)	-234.416244	-234.416244
Sum of electronic and thermal energies (E_h)	-234.408954	-234.408370
Sum of electron and thermal enthalpies (E_h)	-234.408010	-234.406438
Sum of electronic and free energies (E_h)	-234.447849	-234.447398

The energies do not differ by a lot, and in general the energy of the compound at 0K is less negative than that at 298.15K. This might be because the energies at a lower temperature hinders electronic movements.

Optimising "Chair" and "Boat" Transition Structures

In this experiment and "chair" and "boat" transition structures of the Cope rearrangement are looked at and compared against each other.

An allyl fragment (CH₂CHCH₂) was created and optimised under the method of HK/3-21G. A transition state could also be hypothesised. The diagrams below shows the allyl fragment and the proposed Transition State (TS) structure.

Optimisation and frequency analysis of the TS structure was carried out under the HF/3-21G basis set. An imaginary frequency at 818cm^-1 was observed at the results. The animation also proves that this corresponds to the Cope arrangement.

A same calculation is carried out with ModRedundant Minimisation with frozen C-C bond lengths fixed at 2.20Å. Now the imaginary frequency is.

The table below shows the results obtained in the two simulations.

*Table 5: Results obtained for different optimisation methods at TS*
	TS (Berny)	Redundant Coordinate
Allyl C-C bond length	2.021	2.200
Final Energy (Hartree a.u.)	-231.619322	-231.614023
RMS Gradient (a.u.)	0.00005006	0.006031
Dipole Moment (Debye)	0.0017	0.0103
Point Group	C_2h	C_2h
Imaginary Vibration Frequency (cm^-1)	-818	-672.
Jmol

As for the Boat structure, a new method (QST2) was introduced to optimise the compound, which takes the coordinates of the reactants and products into account of the calculation. The Opt+freq job was done with a basis set of HF/3-21G. The outcome was a failure because the reactant and product were too similar and that it could not give the correct transition state geometry. See diagram for the failed optimisation.

Jmol of failed TS:

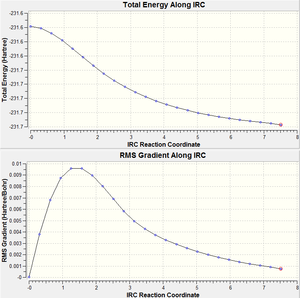
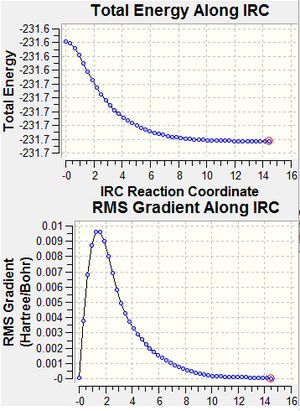
We cannot deduce the geometry of the final product of the reaction between 2 allyl fragments even though both transition state geometries of the boat and chair conformers were obtained. The Intrinsic Reaction Coordinate (IRC) was introduced to calculate the model and this method follows the minimum energy path from a transition structure down its local minimum energy path. This method is applied in two ways: once with only one calculation, the other with calculations at every single step. The second method provides a more accurate result, shown by the lower total energy value by 0.0 a.u. and that the IRC energy curve is closer to the minimum.

From the energy and the point group of the final structure, we may conclude that the chair TS leads to a formation of the Gouche2 conformer, as shown in Appendix2.

*Table 6: Summaries obtained for two IRC optimisation methods at the Chair TS*
	Single Calculation	Calculations at multiple steps
Points on IRC	25	47
IRC energy pathway & RMS Gradient
Structure
Energy/a.u.	-231.688635	-231.691664
Point Group	C₂	C₂

These compounds do not geometrically differ a lot, but as the every step method produces a lower energy, it is believed to be a more accurate method.

In order to compare results between basis sets and boat & chair TS at different temperatures, (@298.15 and 0K)

*Table 7: Summary for the chair and boat transition structures under different temperatures and methods*
	HF/3-21G			B3LYP/6-31G*
	Electronic energy (a.u.)	Sum of electronic and zero-point energies @0K (a.u.)	Sum of electronic and thermal energies @298.15K (a.u.)	Electronic energy (a.u.)	Sum of electronic and zero-point energies @0K (a.u.)	Sum of electronic and thermal energies @298.15K (a.u.)
Chair TS	-231.619322	-231.466345	-231.461344	-234.556983	-234.414599	-234.409001
Boat TS	-231.602802	-231.450586	-231.445302	-234.543093	-234.402063	-234.396007
Reactant Anti2	-231.692535	-231.539170	-234.559704	-234.611705	-234.468904	-234.461875

With the data in the table above, the activation energy of the boat and chair TS reactions could be worked out, shown in the table below:

"Table 8: Summary of activation energies"
	HF/3-21G		B3LYP/6-31G*		Expt.
	@0K	@298.15K	@0K	@298.15K	@0K
Chair TS ΔE	45.70	44.69	34.08	33.18	33.5 ±0.05
Boat TS ΔE	55.59	54.76	41.94	41.33	44.7 ±2.0

The Activation Energies agree with the lit. values at 0K. Since for all temperatures the chair TS ΔE is always lower than that of the boat TS, the chair structure should be the preferred pathway of this reaction.

The Diels-Alder Cycloaddition

Cycloaddition between Cis-Butadiene and Ethylene

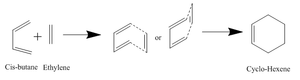
In this part we are investigating the Diels-Alder cycloaddition of butadiene and ethylene. Mechanism of reaction shown in diagram on the right. The molecular orbitals of the reactants and the transition state are looked at.

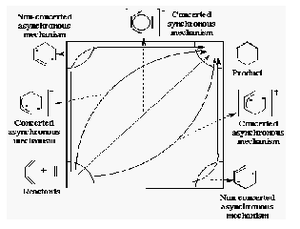
There are two ways of how the reaction transition state could go, synchronous or asynchronous, i.e. either concerted: bond broken then formation, or vice versa. They are shown in the diagram on the right.

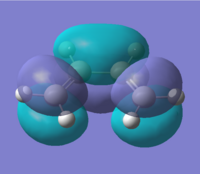
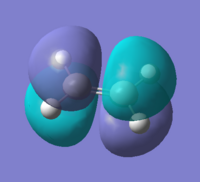
Firstly the cis-butadiene and ethylene were created and optimised using the AM1 semi-empirical molecular orbital method. The interacting molecular orbitals of the reactants are shown below.

*Table 8: HOMO & LUMOs of cis-butadiene & ethylene and their energies*
Molecule	HOMO	HOMO energy (a.u.)	Symmetry	LUMO	LUMO energy (a.u.)	Symmetry
Cis-butadiene		-0.34380	Asymmetric		0.01707	Symmetric
Ethylene		-0.38775	Symmetric		0.05284	Asymmetric

By observing the shapes of the orbitals one would expect the HOMO of the cis-butadiene to react with the LUMO of the ethylene. Also looking at the energy differences between the HOMO-LUMO it is also shown that the HOMO@Butadiene-LUMO@Ethylene has a smaller difference than the other way round. This agrees well with the assumption that cis-butadiene acts as an electron acceptor, with the ethylene being the donor.

The QST2 method was chosen over the TS(Berny) method to investigate the transition state of this experiment due to the accuracy and reasons discussed above. The new bonds formed in the transition state is found to be 2.12Å, which is longer than any C-C bond or the Van der Waals radius (1.70Å). The original sigma bonds are shortened from a typical 1.54Å (C_sp3-C_sp3) to 1.40Å, and the double bond of ethylene about 1.38Å, which is about 0.04Å longer than a typical C=C (C_sp2-C_sp2) bond, which is 1.34Å

[[image:]] The imaginary vibration of this transition state is found to be at -956cm^-1, which indicates the bond formation. The animation of this vibration shows that the vibration is synchronous, i.e. concerted reaction.

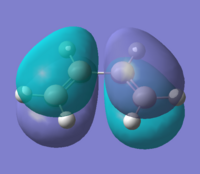
By looking at the HOMO and LUMO at the transition states we could see that they correspond to the HOMOs and LUMOs of the reactants. The HOMO is the interaction between HOMO@Butadiene and LUMO@Ethylene, and the LUMO shows characteristics of HOMO@Ethylene and LUMO@Butadiene.

*Table 9: HOMO & LUMO Cyclohexene and its energies*
HOMO	HOMO energy (a.u.)	Symmetry	LUMO	LUMO energy (a.u.)	Symmetry
Cyclohexene		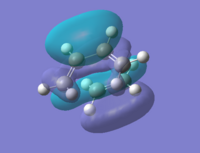-0.34380	Symmetric		0.01707	Asymmetric

Uploaded on D-Space:DOI:10042/to-6330

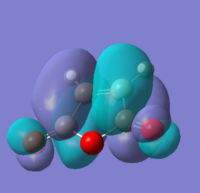
Cycloaddition between Maleic Anhydride with Cyclohexadiene

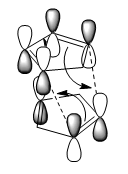
The exo product should be thermodynamically the major product due lower energy, but in real life it is the endo product that dominates.^[2] This could be explained by the Endo Addition Rule,image below shows the secondary orbital interactions, where the non-bonding carbons interact with each other, thus lowering the activation energy of the reaction.

*Table 10: HOMO & LUMOs of Maleic Anhydride & hexadiene and their energies*
Molecule	HOMO	HOMO energy (a.u.)	Symmetry	LUMO	LUMO energy (a.u.)	Symmetry
Maleic Anhydride		-0.059	Symmetric		0.034	Asymmetric
Hexadiene		-0.321	Asymmetric		0.016	Symmetric

References

↑ B.G. Rocque, J.M. Gonzales, H.F. Schaefer III, Mol. Phys., 2002, 100, 441[1]
↑ W.C. Herndon, C.R. Grayson, J.M. Manion, J. Am. Chem. Soc.., 2002, 124, 1130 DOI:10.1021/jo01278a003

[1] B.G. Rocque, J.M. Gonzales, H.F. Schaefer III, Mol. Phys., 2002, 100, 441[1]

[2] W.C. Herndon, C.R. Grayson, J.M. Manion, J. Am. Chem. Soc.., 2002, 124, 1130 DOI:10.1021/jo01278a003

[1]

[2]