Rep:Module2rh1909

Module 2

Structural Analysis of TlBr₃

The ground state geometry of TlBr₃ was optimised using the 'B3LYP' method. The medium level basis set of LanL2DZ was used, which is suitable for heavier elements like those in question here.

Optimised Thallium(III) Bromide

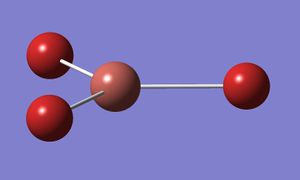
The optimisation gave the following results:

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LanL2DZ
Charge	0
Spin	Singlet
E(RB3LYP) (a.u.)	-91.22
RMS Gradient Norm (a.u.)	0.00
Dipole Moment (Debye)	0.00
Point Group	D3H
Tl-Br Bond Distance (Angstroms)	2.65
Br-Tl-Br Bond Angle (o)	120.0

You can find the TlBr₃ optimisation file by clicking this link. Media:TLBR3_OPTIMISATION.LOG

The Tl-Br bond distance is in relatively good agreement with the observed value of 2.52 Angstroms. The bond angle is also as expected for this molecule with D_3H point group symmetry.

The optimised TlBr₃ molecule was then subjected to a frequency analysis. It is vital that the same method and basis were used otherwise the results are not relative and are uncomparable. The optimised structure is found by the computer after a series of trial and error calculations until the gradient of the Potential Energy Surface curve is equal to zero. The frequency analysis must be carried out in order to confirm that the optimised structure is at the energy minimum and not a maximum. This is done by calculating the second derivative of the PES curve. For the structure to be at an energy minimum, none of the frequency values should be negative. This was the result obtained, all frequencies and intensities are listed in the table below:

Vibrational Mode No.	Frequency (cm-1)	Intensity
1	46	4
2	46	4
3	52	6
4	165	0
5	210	25
6	210	25

See here for a link to the frequency analysis file. Media:ROSEANNA_TLBR3_FREQACTUAL.LOG

This file tells us that the 'low frequencies' are -3, 0, 0, 0, 4 and 4cm^-1. These frequencies correspond to vibrations of the centre of mass of the molecule and are much smaller than the vibrational modes seen in the table. The table shows that the lowest “real” normal mode is 46cm^-1, this corresponds to two vibrational different vibrational modes and would be found at the energy minimum. The first vibration involves two of the bromine atoms moving towards and away from each other with other atoms stationary. The second vibration involves only one bromine atom moving from side to side with all other atoms stationary.

The IR spectrum shows only two peaks. This is because one of the vibrational modes would not show up as it is completely symmetric (all bromine atoms moving in and out in concerted manner with thallium stationary). The other four vibrations are paired off into two sets of degenerate vibrations, so there is no separation of peaks.

IR Spectrum for TlBr3

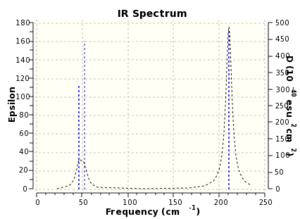
The spectrum is in good agreement with observed literature values for vibrations.

Molecular Orbital Analysis of BH₃

Using the ‘B3LYP’ method with a basis set of ‘3-21G’ a molecule of BH₃ was optimised. The resultant molecule was viewed in Gaussview and it appeared that the bonds had disappeared. Of course, they haven’t disappeared in reality, it’s just that the optimised value for the bond distance is outside a value that was previously defined by Gaussian.

In reality, a bond is an overlapping of orbitals between two atoms, and the electron density from both atoms is spread across the new molecular orbital (of course depending on other properties such as electronegativity). One model describes the LCAO method, whereby atomic orbitals of the same symmetry are linearly combined to give molecular orbitals. These can be depicted in an MO diagram, which has been drawn in this section, along with qualitatively calculating the MOs using Gaussian.

The optimised BH₃ molecule was then subjected to a frequency analysis in order to confirm the structure was at an energy minimum. The table below describes the form of the vibrations, their frequency and intensity, and the symmetry of the vibration in the D_3H point group.

Form of Vibration	Frequency (cm-1)	Intensity	Symmetry D3H Point Group
1 All atoms moving up and down. Three Hs moving in opposite direction to B. ADD MOVIE	1144	93	a2”
2 Two Hs moving simultaneously towards each other, with other B-H stationary	1204	12	e’
3 Two Hs rock left to right in seesaw motion, whilst other H moves left and right simultaneously	1204	12	e’
4 All Hs move in and out in a concerted manner with B stationary	2598	0	a1’ totally symmetric
5 Two Hs move in and out in unconcerted manner with other H stationary	2737	104	e’
6 Two Hs move in and out simultaneously, and other H moves in out in unconcerted manner	2737	104	e’

As you can see, there are no negative frequencies, so the optimised structure is at an energy minimum. Media:ROSEANNA_BH3_FREQ.LOG. The IR spectrum reflects the data. There are only three peaks shown as the dipole moment in vibration 4 is cancelled out due to total symmetry, and there are two

sets of degenerate vibrations.

Infrared Spectrum for BH3

.

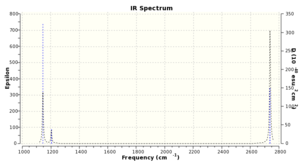
The MOs of the optimised structure were then investigated, and the population analysis can be found by clicking this link. DOI:10042/to-12894 .

Please find here, a diagram of a drawn MO diagram of BH₃ depicting the LCAOs and the MOs calculated from the population analysis. Media:BH3 Molecular Orbital Diagram.docx.

The qualitatively calculated MOs are very similar to the LCAOs for the bonding (and non-bonding) orbitals. So for calculation of the occupied orbitals, the qualitative modelling method seems very accurate. For the anti-bonding orbitals, however, the qualitative MOs have quite different, odd-shaped MOs. For example, the MO corresponding to the 3a₁^’ anti-bonding LCAO, is very different. It actually appears that this MO and the MO for one of the higher energy anti-bonding orbitals should in fact be switched round! This would suggest that the quantum mechanical calculations for determining the energies for these orbitals was not very accurate. In practise however, the need to know a lot of information about these orbitals may not be necessary, because they are so high in energy compared to the HOMO that they may never be occupied or involved in the chemistry of the molecule.

Analysis of the cis and trans Isomer of Mo(CO)₄(PCl₃)₂

The purpose of this section is to analyse the two isomers to find out which one is more stable. Each isomer was first optimised using the ‘LanL2MB’ basis set, the torsion angles between Cl-P-Mo-C were then altered appropriately in the resulting molecules. They were then subjected to another optimisation using the ‘LanL2DZ’ basis set. For the optimisation files for the cis isomer, click this link here. DOI:10042/to-12895 . For the trans isomer, click this link here. DOI:10042/to-12897 .

These isomers can thermally interchange between one another. The results show that the total energy for the cis-isomer is -1637211kJ/mol and for the trans-isomer is -1637208kJ/mol. This means that the trans-isomer is less stable by 3kJ/mol. The calculations for energy are accurate to around 10kJ/mol, so these results cannot be verified. It would be expected that the trans-isomer would be the most stable, mainly due to steric reasons.

By changing the R groups on the PR₃ ligand, you can ‘fine-tune’ the complex in order to make one or the other isomer more stable. Increasing the steric bulk of the PR₃ ligand, greatly increases the stability of the trans-isomer, e.g. PPh₃. In order to make the cis-isomer, a bidentate phosphine ligand could be used.

The frequency analysis of the cis-isomer can be found here. DOI:10042/to-12899 . In the CO stretching region, there are four peaks.

Frequency (cm-1)	Form of vibration
1945	Equatorial COs move in and out in unconcerted manner
1949	Axial COs move in and out, unconcerted
1958	Axial COs move in and out in a concerted manner, whilst equatorial COs move OUT and in
2023	All COs move in and out in concerted fashion

There are some very low frequencies present in the results at 11cm^-1 and 18cm^-1. After animating the vibration, it was seen that they correspond to a twist in the Mo-P bond. For example, the vibration corresponding to 11cm^-1, involves Mo-P bond twisting in opposite directions causing the whole complex to tilt forwards and backwards in

an oscillating motion.

Picture showing form of low frequency vibration in cis-Mo(CO)4(PCl3)2

These vibrations are of such low energy that they will

be occurring rapidly and constantly at room temperature.

The frequency analysis of the trans-isomer can be found here. DOI:10042/to-12900 . This time in the CO stretching region there is only one peak.

Frequency (cm-1)	Form of vibration
1950.47	Two equatorial trans-COs move in and out in concerted manner
1951.12	Other two equatorial trans-COs move in and out in concerted manner

There is only one peak for the trans-isomer compared to the cis-isomer due to the increase in symmetry of the CO groups in the trans-isomer. If you look at the frequencies in the CO stretching region, there are actually four, however, these correspond to totally symmetric vibrations, therefore no dipole moment, and no intensity on the IR spectrum. The cis-isomer has COs in non-symmetric positions, therefore the CO stretched are all visible on the spectrum.

There are also some very low frequencies present in the results for the trans-isomer, e.g. 5cm^-1 and 6cm^-1. These also correspond to a twisting of the P-Mo bond. For example, the vibration corresponding to 5cm^-1 is a twisting of P-Mo bonds in same direction. The fact that these vibrations are of such a low energy, suggests that the P-Mo bond itself must be relatively weak. This is as expected because the PCl₃ ligand is known to be a poor π-donor (due to electronegative chlorine atoms). This also helps to explain the high frequency values for both complexes. As PCl₃ is donating little to the metal centre, less electron density is available for Mo-C back-donation, and therefore the CO bond remains very strong.

Below are bond distances and angles measured for each isomer.

Bond or Angle	Cis-isomer (distance in angstroms, angle in deg)	Trans-isomer (distance in angstroms, angle in deg)	Difference
Mo-P	2.51	2.44	0.07
Mo-C(eq)	2.01	2.06	-0.05
Mo-C(ax)	2.06	-	-
C-O	1.17	1.17	0
P-Cl	2.24	2.24	0
Mo-P-Cl	116.0	117.3	-1.3
Cl-P-Cl	100.2	99.1	1.1

The Mo-P bond in the cis isomer is 0.07 angstroms longer than in the trans isomer. This is as expected if the trans isomer is more stable. The steric strain in the cis isomer weakens the Mo-P bond slightly. The Mo-P-Cl bond angle is 1.3^o smaller in the cis isomer. The PCl₃ ligand is under more strain in the cis isomer, this is demonstrated by this result. All bond distances and angles are comparable to literature values.

Exploring Bonding in Aluminium Halides

It is known that aluminium halides Al₂X₆ (X = Cl, Br) form 3 centre-2 electron bonds, with the halides in a bridging position. In this modelling experiment, the bonding situation will be investigated for three isomers of Al₂Br₂Cl₄ in order to determine the effect of bromine atoms on the compound and the stability of each isomer. The three isomers in question are shown in the

picture.

Al2Br2Cl4 Isomers

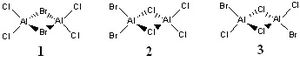
First, the bonding in Al₂Cl₆ will be investigated. Before being optimised, the bond lengths and angles were altered to be as near to observed values as possible. . The molecule was then subjected to an optimisation and then frequency analysis using the ‘B3LYP’ method with the ‘6-31G’ basis set. The total energy of this molecule was found to equal -3246.320a.u. Click these links for the result of these analyses. Optimisation file DOI:10042/to-13028 . Frequency analysis DOI:10042/to-13030 .

Below is a table describing the geometry of the compound. As expected for a 3c-2e bond, the bridging chlorine atoms have longer bond lengths than the terminal ones.

Bond Distances (Angstroms)	Bond Angles (o)
Al-Clt	2.17	Clt-Al-Clb	110.3
Al-Clb	2.41	Clb-Al-Clb	86.4
		Clt-Al-Clt	123.3

Below is a table showing the results of the frequency analysis. The IR spectrum shows seven peaks. The higher frequency vibrations correspond to movements of the aluminium atoms, and the lower frequencies correspond to chlorine atom vibrations. This is expected because the chlorine atoms are more freely able to move without affecting the whole molecule (compared to the aluminium atoms).

No.	Form of Vibration	Frequency (cm-1)	Intensity
1	Al atoms move up and down, concerted, with all other atoms stationary	580	258
2	Al atoms move side to side, concerted, with all others stationary	437	365
3	Al atoms move into and out-of-plane	355	153
4	Clb atoms shorten and lengthen in concerted manner	277	103
5	Clb atoms move up and down in concerted manner	159	18
6	Clt atoms move towards and away from each other, causing seesaw motion of molecule	124	25
7	Clt atoms move into and out-of-plane, concerted.	113	14

In order to analyse the bonding correctly, (and to calculate the energy of formation of the dimer), two AlCl₃ fragments will be used, and the NBO analysis results studied. The optimisation and frequency analysis of this fragment were carried out using the same method and basis set as for the dimer. Optimisation file: DOI:10042/to-13033 . Frequency analysisDOI:10042/to-13034 . The total energy of the fragment was found to be equal to -1623.144a.u. This can be used to calculate the energy of formation via this equation:

ΔE = E(Al₂Cl₆)-E(AlCl₃)+E(AlCl₃)

This gives a value of -83.49kJ/mol (4s.f.)

The .log file containing the NBO analysis was then studied: DOI:10042/to-13035 . This describes the bonding in the molecule, and we are able to see that an sp² hybridised Al orbital forms a bond with a chlorine atomic p-orbital. Looking at the ‘Perturbation Theory Analysis’ section, gives us details of the acceptor and donor ability of each atom in the molecule and can be used to see why AlCl₃ readily dimerises. These results shows that if a lone pair on a chlorine atom (LP) were to donate itself into an empty p-orbital on an aluminium atom (LP*) this gives a stabilisation energy (E(2)) of 67.82kJ/mol. This gives the largest stabilisation energy of all possible donations, and so would be the expected method of bonding in the dimer.

Now to look at the three Al₂Br₂Cl₄ isomers. Below is a table showing the geometries of the three isomers. See optimisation files here. Isomer 1: DOI:10042/to-13036 . Isomer 2: DOI:10042/to-13037 . Isomer 3: DOI:10042/to-13038 .

Bond Distances (Angstroms)	Bond Angles (o)
	Isomer 1	Isomer 2	Isomer 3		Isomer 1	Isomer 2	Isomer 3
Al-Clt	2.18	2.17	2.17	Clt-Al-Clt	123.0	122.5	-
Al-Brt	-	2.29	2.29	Clt-Al-Brt	-	-	124.3
Al-Clb	-	2.42	2.41	Brt-Al-Brt	-	129.1	-
Al-Brb	2.52	-	-	Clt-Al-Clb	-	110.3	110.3
				Clt-Al-Brb	109.6	-	-
				Brt-Al-Clb	-	108.2	108.2
				Clb-Al-Clb	-	86.7	87.2
				Brb-Al-Brb	90.4	-	-

These results show that the bromine bridging bond is larger than the chlorine bridging bond and possible, therefore, less stable. This could be due to steric strain in the four atom central ring.

Below is a table showing the results of the frequency analysis for all three isomers. The frequencies have been paired up with the same vibrations described for Al₂Cl₆. See frequency analysis files here. Isomer 1: DOI:10042/to-13039 . Isomer 2: DOI:10042/to-13040 . Isomer 3: DOI:10042/to-13041 .

Vibration No.	Frequency (cm-1)	Intensity
	Isomer 1	Isomer 2	Isomer 3	Isomer 1	Isomer 2	Isomer 3
1	571	571	561	239	160	249
1(a)	-	531	-	-	88	-
2	431	465	399	321	91	396
2(a)	-	388	-	-	293	-
3	332	353	352	144	137	137
4	233	289	260	93	38	54
4(a)	-	250	-	-	27	-
5	126	152	149	11	15	14
6	112	109	109	16	16	19
7	103	108	107	11	9	10

From the IR spectra, you can see that isomer 2 has three more peaks than 1 & 3. This is because it is less symmetrical compared to the other isomers. These extra peaks correspond to vibrations 1(a), 2(a) and 4(a). The pairs of vibrations correspond to one large stretching motion on the terminal chlorine side and little on the bromine side, and vice versa for the other vibration (a) in the pair. As a result, the intensities of these vibrations are also smaller than for the other isomers. The majority of the frequencies for isomer 2 are all also higher energy than the others. This may be due to the two terminal bromine atoms being in a closer proximity to each other.

Using the same method as for Al₂Cl₆, the energy of formation of the three isomers was calculated.

	Isomer 1	Isomer 2	Isomer 3
Total Energy (a.u.)	-7469.1311	-7469.1311	-7469.1312
ΔE (kJ/mol)	-104	-105	-106

As you can see, there is little difference between the total energies of the molecules and the energy of formations. However, one thing to notice is the difference between these values for ΔE and the value of ΔE for Al₂Cl₆, which is considerably ‘less negative’, showing that the addition of bromine into these molecules makes them overall more stable.

In order to calculate which isomer is most stable, we must look at the NBO analysis of each possible fragment. These fragments are AlBrCl₂ and AlBr₂Cl. File for AlBrCl₂ fragment: DOI:10042/to-13042 . File for AlBr₂Cl fragment: DOI:10042/to-13043 . For isomer 1, the .log file was studied and showed that the stabilisation energy, E(2), for the dimerization where a lone pair in a p-orbital on a bromine atom (LP) was to be donated into the antibonding Al-Cl bond (BD*) is 29.00kJ/mol. All results are tabulated below.

	Orbitals involved in Donation	Stabilisation Energy (kJ/mol)
Isomer 1	p-Br LP à Al-Cl BD*	29.00
Isomer 2	p-Cl LP à p-Al LP*	69.71
Isomer 3	p-Cl LP à Al-Br BD*	66.74

From these results, you can see that the most stable isomer is isomer 2. The stabilisation energy for isomer 1 is more than half the other two, showing bromine’s in a bridging position are less stable than chlorine atoms.

Isomer 2 shows different orbitals being involved in the bond formation. Rather than the chlorine lone pair being donated into the Al-X antibond, it is donated into an empty non-bonding p-orbital of lower energy.

Conclusion

As you can see, the in-depth study of Al₂Cl₆ and the three isomers of Al₂Cl₆ showed a number of things. The optimisation and frequency analysis of Al₂Cl₆ showed that it’s energy of formation is ‘less negative’ than when bromine atoms are involved, showing that bromine stabilises the isomers in some way.

The geometric analysis of all compounds showed that the bridging bonds were longer than the terminal ones. This is in accordance with the known 3c-2e bonding present in these molecules. The bridging bonds are weaker and have a lower bond order because of this.

The frequency analysis of all compounds showed that the higher energy vibrations are due to movement of aluminium atoms, with vibrations largely involving the halide atoms at lower energy vibrations. There appears to be little difference between chlorine and bromine vibrations.

The total energies and ΔE values are very similar for all three isomers. The NBO analysis of all three isomers allowed us to find out the stabilisation energy upon donation of electrons to the aluminium atoms. These results were more decisive and showed that isomer 2 was the most stable.