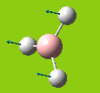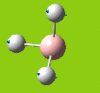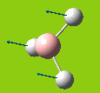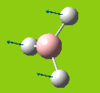Rep:Module2:scastiglione1

Module 2: Bonding (Ab Initio And Density Functional Molecular Orbitals)

Computational Lab Module 2

S.Castiglione

Introduction

Computational chemistry gives us insight into the structure and bonding of complexes. Whilst bonding in organic systems is, mostly, relatively straight forward, for inorganic compounds it is often more complex. Computational studies can not only be used to differentiate between the energy of stable conformers, but also to discover the location of transition states and activated complexes that may be difficult to characterise experimentally.

Thermodynamic information can be obtained from the energy of stable states, and from the energy of a transition state, and we can also obtain kinetic data. With recent advancements an increasing number of properties can be evaluated, for example many spectra and dipole moments, and analysis of the electron density can give us information on the bonding and local interactions between atoms.

A number of experiments will be carried out which will analyse certain molecules to extract some of the information mentioned above.

Many of the pictoral files below are present as thumbnails and should be opened to show the larger file. This is to speed up the loading of the page.

All errors stated below are assumed henceforth;

Energies will have an error of ≈ 10 kJ/mol ~ 3.8 x10^-3 a.u. The dipole moment will be accurate to ~ 2 decimal places ~ 0.01 Deby. Frequencies (cm^-1) are accurate to 0 decimal places, (systematic error of around 10%). Intensities are rounded to the nearest whole integer although the accuracy is much less that this. Bond distances are accurate to ≈ 0.01 Å . Bond angles are accurate to ≈ 0.1°.

Part 1: Optimising a Molecule of BH₃

The first part of this module involves familiarisation with the neccessary procedures used on gaussview to effect the optimisation of a molecule of BH₃.

BH₃

Pre And Post Optimisation BH₃ Values

[Pre] H-B Bond Length	1.18 Angstroms	[Post] H-B Bond Length	1.19 Angstroms
[Pre] H-B-H Angle	120.0oC	[Post] H-B-H Angle	120.0oC

Optimised BH3

Generated BH3 Summary

RMS And Energy Gradient Graphs

After drawing the BH₃ molecule an initial optimisation was run using the B3LYP method and 3-21G basis set. The Pre and Post optimisation values for the bond lengths and angles are shown in the table to the left. The angle in both cases is 120 degrees which is unsurprising and agrees with VSEPR Theory. The original and optimised geometries have D3h point group symmetry.

From the summary file one can extract information about the calculation, for instance one can see that the calculation type is FOPT, the calculation method is RB3LYP, the basis set is 3-21G, the final energy in atomic units is -26.46 a.u., the dipole moment is 0.00 Debye and the gradient is 0.00 a.u. One can see that the gradient is nearly zero (the exact number presented is 0.00004507 a.u.). This shows the calculation has not gone awry. The log file can also be examined to see the details of the calculations.

The RMS and Energy curves (with relation to number of optimisations) can be viewed also when an optimisation has been run. The graphs' final point represent the energy and RMS gradient of the final geometry, and if the lowest energy geometry is present, the gradient is zero. The RMS shows the derivative of the energy with respect to the spatial separation of atoms and the optimisation searches for when the rate of change of energy with respect to distance becomes zero.

Jmol rotatable BH₃ molecule.

Press the buttons below to open up Jmol files for the molecule.

Part 1.1: MO Diagram Of BH₃

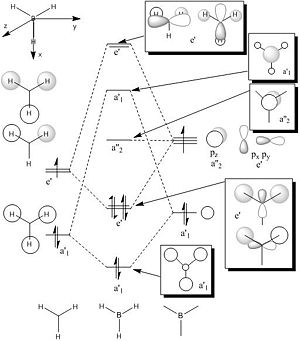
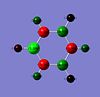
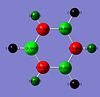
The BH₃ (D3h symmetry) molecular orbitals were calculated and visualised in Gaussview.

Orbitals

Orbital Symmetry	LCAO representation	Gaussview Visualisation
a1'
e'
e'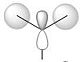
a2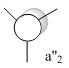
a1'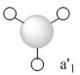
e'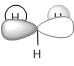
e'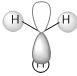

MO Diagram Of BH₃

To calculate the molecular orbitals an nbo analysis was run .The MOs can be seen in the table below alongside their LCAO counterpart. The MO diagram for BH3 was drawn in ChemDraw. The atomic orbitals of the same symmetry are mixed to form the corresponding molecular orbitals.

The 'nbo' part of the calculations is for the 'natural bond orbital' method. The nbo investigates the charge distribution and the molecular orbitals in a more localised manner, and upon invesigation of the log file one can see the total charge is equal to zero, as one would expect for a neutral molecule, and the hydrogens all have the same value, as one would expect from the symmetry. The log file shows, for the hydrogen atom a full s contribution (unsurprisingly) and for the boron atom, a 1/3 contribution from the s orbital and a 2/3 contribution from the p orbitals so it would appear the boron bonds are sp2 hybridised.

One must consider is the difference between the qualitative and quantiative MOs. The calculated and qualitative counterparts are very similar despite the different prediction methods. If one takes the qualitative drawings and imagines how the orbitals of the same phase would interact one might reasonably be expected to come up with an image similar to that which was predicted in the calculation. The closer in energy the atomic orbital is to the MO the more it contributes to that MO. The issue with this is that in order to get quantitative energies of the MOs one must use quantitative MO calculations.

The phase distribution in both models match well which would suggest that the theories work well in predicting relative energies for simple molecules. It is difficult to predict however how stabilised or destabilised the bonding and anti-bonding orbitals are, but this is where computational chemistry is useful to determine the energies of said orbitals relative to one another.

Part 1.2: Vibrations Of BH₃

Vibrations Of BH₃

Number	Image	Form	Frequency / cm-1	Intensity	D3h Symmetry Sub Group
1		Stationary boron, hydrogens move synchronously	1118	96	a2' ' wagging
2		Boron and one hydrogen stationary, two B-H bonds bend	1186	11	e' scissoring
3		Boron stationary, B-H bonds bend	1186	11	e' scissoring
4		Boron stationary whilst B-H bonds stretch symmetrically	2688	0	a1' symmetric stretch
5		Boron and one hydrogen stationary, asymmetric stretch of B-H bonds	2834	102	e' asymmetric stretch
6		Boron stationary, two B-H bonds stretch in phase, out of phase with the other	2834	102	e' symmetric / asymmetric stretch

BH3 Frequency Summary

BH3 Frequency Real File

BH3 IR Spectrum

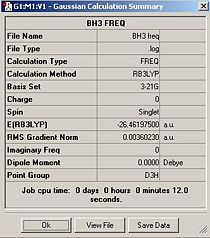
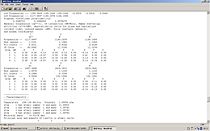
The vibrations of trigonal planar BH₃ were calculated and visualised in Gaussview. They are summarised in the table.

Whilst there are six BH₃ molecule vibrations, only 3 peaks are visible on the IR spectrum.

This is because the 6 vibrations have only 4 different frequencies, and the intensity of one of these vibrations is zero. This intensity is zero as there is no change in dipole moment during the vibration. The degenerate peak pairs (at 1186.21 and 2834.38 cm^-1) show up only once and the zero intensity vibration at 2687.50 cm^-1 does not show up.

In the literature the peaks are at 1206, 1387 and 1995 cm^-1 instead of 1117.58, 1186.21 and 2834.38 cm^-1. This is not a brilliant match and means the calculations used are not perfect.

Part 2: Optimising a Molecule of BCl₃

BCl₃

Pre And Post Optimisation BCl₃ Values

[Pre] Cl-B Bond Length	1.87 Angstroms	[Post] Cl-B Bond Length	1.86 Angstroms
[Pre] Cl-B-Cl Angle	120.0oC	[Post] Cl-B-Cl Angle	120.0oC

Optimised BCl3

Generated BCl3 Summary

Pseudo potentials and larger basis sets will be used to run an optimisation for a moelcule of BCl₃. The method is much as before except the symmetry is being restrained to D3h and the medium-level basis set of LanL2MB will be used.

The angles and bond lengths before and after optimisation are shown in the table. The summary shows the details of the optimisation (The file type is .log, the calculation type is FOPT, the calculation method is RB3LYP. the basis set is LanL2MB, the final energy is -69.44 a.u. , the dipole moment is 0.00 Debye, the point group is D3h and the calculation time is 21.0 seconds).

BCl₃ Frequencies

Mode	Frequency / cm-1	Intensity	Image	Mode	Frequency / cm-1	Intensity	Image
1	214	4		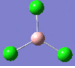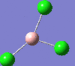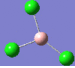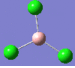2	214	4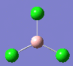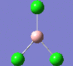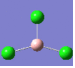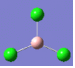
3	380	44		4	413	0
5	932	259		6	932	259

Generated BCl₃ Frequency Summary

The same basis set was used for the frequency calculation as the geometry optimisation. It is important to use the same basis set as the frequency is the second derivative of the potential energy curve, and so if a different basis set was used one might have a different potential energy curve and you would not accurately be able to compare the two. The energy calculated for the optimisation and frequency calculations was the same as the same basis set was used.

One must carry out a frequency analysis to find out if the molecule you have is at the minimum energy for the molecule. The frequency is the second derivative of the potential energy curve so if the value is greater than zero, the energy is at a minimum.

As you can see here, all of the wavenumbers are positive and so this means the BCl3 molecule must be in a potential well and therefore at a minimum energy. Because all of the values are positive, it means I am at the total minimum of the molecule, the lowest global minimum. If say one of them was negative, this would mean I could be in a local minimum with respect to the potential energy, but not the total global minimum energy of the whole molecule.

The calculated optimised bond length is 1.866 angstroms whilst the literature cites 1.73±0.02 angstroms. The angle cited from the same reference is 120±3 degrees which matches the 120 degrees calculated in the optimisation. The bond length value is quite different to the literature value so the basis set is obviously still limited. Perhaps a larger basis set would have produced a better result. One would expect the molecule to have D3h symmetry and this is what Gaussview produces (unsurpisingly as we constrained the symmetry to D3h). Gaussview can used the specified point group to quickly optimise the molecule as it knows what symmetry elements to aim for.

When Gaussview runs optimisations it does not initially draw in the bonds. Gaussview has programmed limits and when the two bonded atoms are at a distance too large for the electron interactions to be considered 'bonding' the bonds are not drawn. Gaussview sees the bonds as the localisation of electron interactions and when they are too far apart the bond is too weak and is not initially drawn in. It doesn't mean the bond is not there.

A bond can be seen as a pair of electrons shared between a pair of atoms or as an area of electron density holding two positive nuclei together, i.e. a molecular orbital, formed from atomic orbitals of the previously aforementioned positive nuclei. An occupied molecular orbital between two atoms is a bond regardless of the distance between them, but if the distance is larger than that specified by Gaussviews parameters it will not see it as a bond.

Jmol rotatable BCl₃ molecule.

Press the buttons below to open up the Jmol file for the molecule.

Part 3: Cis And Trans Isomerism

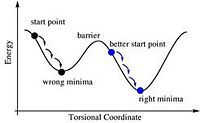
In this section the molecule MoCO)₄L₂ where L=PPh₃. The number of CO vibrational bands active is related to the symmetry of the complex, with four carbonyl absorption bands expected from the compound with cis ligands whilst only one band is expected from the compound with trans ligands. Calculating the full molecule is too expensive in computing resources, so the phenyl rings will be replaced the less computationally demanding Cl atoms which have been shown to have a similar electronic contribution to the bonding as phenyl groups, and they are sterically quite large. I will use calculations to predict the relative thermal stability and the spectral characteristics of the two isomers to determine which isomer is more stable and what the vibrational modes look like.

It is easy, if you don't start in exactly the right orientation, to find a minima that is not the lowest energy one, as shown in the diagram to the above left. For this reason a specific starting point was described and used to get the correct orientation. For the cis conformer one Cl points up parallel to the axial bond, and one Cl of the other group points down, and for the trans conformer, both PCl₃ groups are eclipsed and one Cl of each group lies parallel to one Mo-C bond.

Carbonyl IR Frequencies

Molecule	Mode	Frequency/ cm-1	Intensity	Visualisation	Explanation
Trans	42	1939	1606		2 opposite CO asymmetric stretch
Trans	43	1940	1606		Other 2 opposite CO asymmetric stretch
Trans	44	1967	6		4 CO asymmetric stretch
Trans	45	2025	5		4 CO symmetric stretch
Cis	42	1939	1597		4 CO symmetric stretch
Cis	43	1942	821		4 CO asymmetric stretch
Cis	44	1953	592		4 CO asymmetric stretch
Cis	45	2019	541		4 CO symmetric stretch

Cis Mo(CO)4(PCl3)2 IR Spectrum

Trans Mo(CO)4(PCl3)2 IR Spectrum

These molecules were first optimised using the B3YLP method and the LANL2-MB basis set, and then using this geometry they were further optimised using the more advanced LANL2-DZ basis set which was used for the frequency calculations also. Using this second optimisation the dihedral angles are mostly zero degrees. This more advanced basis set takes into accound d orbitals and all the frequency results were positive which is indicative of the global minimum.

The carbonyl stretches are shown in the table to the left. Whilst there are 4 C=O vibrations for both only 2 are of high intensity for the trans ligand, and as they are at the same frequency it gives only one peak on the spectrum. For the cis liagnd all 4 C=O stretches have high intensity and are at different frequencies so they are resolved individually.

Low Frequency Vibrations

Cis	Cis	Trans	Trans

The experimental values for the cis ligand are at 1867, 1896, 1924, and 2026 cm^-1, and for trans at 1889 cm^-1. Only the 2026 cm^-1 band is a good match. The others are a fair bit off, but the literature is for a PPh₃ ligand and I have used PCl₃ so perhaps this is not so surprising.

There are some very low frequency stretches which are localised throughout the whole molecule and appear in both the cis and trans isomers. These are shown in the table to the left and all appear at frequencies below 50 cm^-1. Theese vibrations are extremely asymmetric and are likely to be due to thermal excitation.

Energies Of The Isomers
(Please excuse the large no. of
decimal places, they are neccessary to see
the difference)

	Cis Isomer	Trans Isomer
Energy / a.u.	-623.69291196 a.u	-623.69414907 a.u
Energy / kJ/mol	-1637508.988 kJ/mol	-1637505.74 kJ/mol

These energies are very similar with the cis form being slightly more stable. The energy difference is 3.248 kJ/mol which is a fairly small amount compared to the energy of the molecule. The cis isomer is more stable due to back bonding from the Moylbdenum d orbitals into the C=O ligands. In the trans configuration, the C=O ligands will compete for the back donation of the same metal d-orbital, resulting in less stabilising back bonding in total as some of the d orbitals are not in the correct geometry to donate into an empty C=O anti bonding orbital. The cis compound has more opportunity for back bonding so there is a stabilisation in energy. The triphenylphosphine/ trichlorophosphine ligands are also capable of participating in this back donation and so they will compete with the carbonyl ligands.

Isomer Mo-P Bond
Lengths (Angstroms)

Cis Isomer	Trans Isomer
2.48	2.42

The literature cites the bond length (trans only) as 2.5 angstroms. This literature value is quite similar to the computed values, although closer to that for the cis isomer which has a longer bond than the trans.

The cis Cl-Mo-Cl bond angle was computed to be 94.3 degrees and the trans angle was 176.8, ie. very nearly right angles and a linear arrangement respectively, suggesting a nearly perfect octahederal arrangement.The literature cites the cis angle as 104.5 degrees, 10 degrees larger, however the reference molecule is for a PPh₃ ligand which is larger and will sterica;ly require more space and may distort this angle.

Jmol rotatable molecules.

Press the buttons below to open up Jmol files for the molecules.

Part 3.1: (Optional) Fine Tuning Catalytic Behaviour

Energies Of The Mo(CO)4(P(CH₃)₃)₂ Isomers

	Cis Isomer	Trans Isomer
Energy / a.u.	-773.36024021 a.u	-773.35736965 a.u
Energy / kJ/mol	-2030457.311 kJ/mol	-2030449.774 kJ/mol

There are two clear ways to change the behaviour of this ligand, to change the steric bulk or to alter the electronic properties by introducing more electron withdrawing or donating groups. In an attempt to fine tune the catalytic behaviour and to stabilise the trans isomer over the cis isomer I have replaced the Cl atoms on the PL₃ ligands with methyl groups. This gives cis and trans Mo(CO)₄(P(CH₃)₃)₂ and we can now see what the effect of changing the ligands are. It turns out that by replacing the Cl's with methyl groups, the trans isomer becomes relatively more stable, by 7.5371152kJ/mol, in agreement with the literature I found on this product which confirms this computed observation. Whilst not as large as a triphenylphosphine group this trimethylphospine group is larger than the standalone Cl ligands. Larger groups will favour the increased separation of the ligands and so as we can see the trans isomer becomes more stable. Interestingly this would suggest that the trans isomer of Mo(CO)₄(PPh₃)₂ may be more stable than the cis isomer as the electronic contribution of the PCl₃ ligand is similar to that of the PPh₃ ligand.

Carbonyl IR Frequencies

Molecule	Frequency/ cm-1	Intensity
Trans	1844	1979
Trans	1844	1983
Trans	1885	5
Trans	1956	2
Cis	1851	1949
Cis	1855	1040
Cis	1873	676
Cis	1960	352

Isomer Mo-P Bond
Lengths (Angstroms)

Cis Isomer	Trans Isomer
2.65	2.53

The comparative CO stretches to the previous molecule are shown in the table, and as can be seen, there are 4 cis C=O peaks of resolvable intensity and one trans peak. The literature places the peaks for the cis isomer at 2019, 1922,1905 and 1899 cm^-1 and at 1895 cm^-1 for the trans isomer. These values are all c. 50cm^-1 off the computed values which is not too bad.

The Mo-P bond lengths are longer in this molecule, as I would expect as this places the bulkier ligands further out and I would expect them to be even longer in a Mo(CO)₄(PPh₃)₂ molecule.

Jmol rotatable molecules.

Press the buttons below to open up Jmol files for the molecules.

Published Optimisation Files;

(LANL2-MB)

Trans Mo(CO)4(PCl3)2 OptimisationCis Mo(CO)4(PCl3)2 Optimisation

(LANL2-DZ)

Trans Mo(CO)4(PCl3)2 OptimisationTrans Mo(CO)4(PCl3)2 FrequencyCis Mo(CO)4(PCl3)2 OptimisationCis Mo(CO)4(PCl3)2 Frequency

Trans Mo(CO)4(PMe3)2 OptimisationTrans Mo(CO)4(PMe3)2 FrequencyCis Mo(CO)4(PMe3)2 OptimisationCis Mo(CO)4(PMe3)2 Frequency

Part 4: (Optional) The Quantum Nature Of Ammonia

Ammonia Inversion

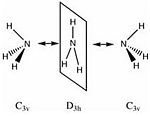
A low potential barrier exists between two the inverted structures of ammonia, this processes is achieved by the hydrogen atoms quantum tunnelling from one side of the nitrogen atom to the other. This purely quantum phenomenon causes "inversion doubling" of the vibrational modes of ammonia. The ammonium molecule can thus be used as a " a quantum information unit. Then the ammonia molecule flips between these two states many times a second. However a linear combination of these two states forms a "stationary state" (a state that does not change over time). The two physical states form '+' and '-' stationary states (which are eigenvectors of the system Hamiltonian). A quantum computer will force a change from one state to the other and this is equivalent to the 0 and 1 of ordinary electron based computing.

6-31g Optimised NH₃

Symmetry	C3v	C1	D3h
Bond Angle (degrees)	109.5	116.0	120.0
Bond Length (angstroms)	1.00	1.01	1.01

Ammonia Molecule

631-G D3h Summary

NH₃

In the first part of this section I will look at different isomers for NH₃ and the effect of symmetry on the structures, energies and optimisation time of these structures. The 3 symmetries for NH₃, C1, C3v, and D3h are related to one-another; C1 is a sub-group of C3v which is a sub-group of D3h.

The molecule was first optimised with the B3LYP method and 6-31G basis set, which is more advanced than the 3-21G basis set., and optimised into the C3v, C1 and D3h symmetries. The D3h symmetry is most dissimilar to the other two, as expected as a dummy atom was used in its creation.

When optimising a molecule, the atoms are moved and the program will try to maintain the symmetry of the molecule. The more symmetrical the molecule the shorter the time it should take to optimise. This is because the program does not have as many different choices for moving the atoms because any movement would need to conserve the said symmetry. The most asymmetric molecule, therefore, would take the longest time to optimise because if the ignore symmetry option is utilised any movement of the atoms is possible and more calculations can be run. These calculations have more possible geometries and thus take longer to optimise.

IR Frequencies Of NH₃ And Literature Values

C3v	C3v	C3v	C3v	C3v	D3h	D3h	D3h	D3h	D3h
Frequency / cm-1	Intensity	Image	Description	Symmetry	Frequency / cm-1	Intensity	Image	Description	Symmetry
459 Lit. 932	595		wagging	a1	89 Lit. 932	838		wagging	a' '2
1681 Lit. 1626	41		scissoring	e	1658 Lit. 1626	53		scissoring	e'
1681 Lit. 1626	41		scissoring	e	1658 Lit. 1626	53		scissoring	e'
3576 Lit. 3337	0		symmetric stretch	a1	3524 Lit. 3337	0		symmetric stretch	a'1
3776 Lit. 3444	7		asymmetric stretch	e	3737 Lit. 3444	18		asymmetric stretch	e'
3776 Lit. 3444	7		symmetric/asymmetric stretch	e	3737 Lit. 3444	18		asymmetric stretch	e'

631-G C3v Summary

631-G C1 Summary

IR Spectrum of C3v NH₃

IR Spectrum of D3h NH₃

In most cases the literature frequencies and computed values match well, apart from the lowest energy frequency. This is likely due to quantum effects not taken into account by the simple basis set. As C3v is a sub-set of D3h equivalent vibrations can be found in each case and the corresponding modes shown are very similar with modes 4, 5 and 6 at almost exactly the same frequencies.

In general, a molecule with greater symmetry is higher in energy than an isomer of lower symmetry, so it is unsurprising to find that the C1 structure is lowest in energy, closely followed by C3v, then D3h, as shown in the summary files. These energy differences are due to the difference in symmetry. Second order Jahn-Teller (distortion due to non degenerate orbital mixing) effects stabilise the D3h molecule by breaking its symmetry via an umbrella motion of the hydrogens converting into a C3v symmetry molecule which allows ground and excited state orbitals to mix. The umbrella motion was visualised using the provided log file, and this umbrella motion is behind the inversion. This alteration of the geometry lowers the total energy. On a potential energy surface the D3h is the transition state and the C3v molecule is the minimum. The C1-C3v energy difference is very small because the pre-optimisation difference, a small change in bond length, is only a small change. The Jahn-Teller effect lowers the energy of a high symmetry molecule by distorting it to a lower symmetry.

Using the more advanced 6311-G basis set and the MP2 method including all electrons (which takes into account the dynamic positions of electrons), we can probe the planar transition state and looking at the vibrations one can see the D3h molecule now has a negative frequency vibration at -320cm^-1. This negative frequency is characteristic of a transition state. This vibration is the mode 1 vibration and corresponds to the mode 1 vibration in C3v also. This vibration follows the inversion reaction path. This is the only vibration which causes the molecules to appear the same as they should from the inversion mechanism. This more advanced calculation takes approximately 8 seconds longer than the prior calculations.

The energy difference between the D3h and C3v conformers is larger with this second calculation (0.01 a.u.(~ 26.25 kJ/mol) compared to 0.00034 a.u.) and is close to the experimental value of 24.3kJ/mol. Thermal energy at room temperature is much lower than the calculated inversion barrier when calculated with the advanced basis set. This means that temperature induced vibrations are not responsible for interconversion at room temperature. It is in fact believed to be due to quantum tunneling. Taking this into account the inversion doesn't need to overcome the energy barrier as tunneling has little temperature dependance.

Jmol rotatable NH₃ molecules.

Press the buttons below to open up Jmol files for the molecules.

Part 5: Mini Project: Benzene, Borazine, Hypothetical Intermediaries And The Effect Of Atom Subsitution

Part 5.1: Introduction

This project is split into two parts. In the first I intend to examine and compare the known compounds Benzene, Borazine and 1,2,Azaborine, and the unknown compounds 1,2,3,4 Diazadiborine and 1,2,4,5 Diazadiborine which are known only when stabilised by ligands or in large spherical buckminster fullerine - like structures. In the latter I intend to examine the effect of replacing an atom in benzene or borazine by a silicon or phosphorous atom and to investigate the reprocussions of these alterations on the properties of the molecules.

For all structures examined the molecules were first optimised using Gaussview on the laptop and then subsequent analysis was achieved using the SCAN web service. Structures were optimised with the DFT:B3LYP method and 6-311G (d,p) basis set and checked afterwards by frequency analysis. This basis set is appropriate for these quite small molecules. All subsequent calculations were performed with this method and basis set also.

Part 5.2: Rotatable Jmol Files

Press the buttons below to open up Jmol files for the molecules.

1,2,3,4 Diazadiborine

1,2,4,5 Diazadiborine

Benzene

1,2 Azaborine

Borazine

Benzene To Borazine

Hypothetical Compounds

P Replacing N Borazine

Si Replacing B Borazine

Si Replacing N Borazine

P Replacing C Benzene

Si Replacing C Benzene

P Replacing B Borazine

P and Si Benzene/Borazine

Part 5.3: Benzene To Borazine

Benzene, 1.2 Azaborine and Borazine

Hypothetical 1,2,3,4 Diazadiborine and 1,2,4,5 Diazadiborine

In this first section I mean to examine and compare the known compounds Benzene, Borazine and 1,2,Azaborine, and the unknown compounds 1,2,3,4 Diazadiborine and 1,2,4,5 Diazadiborine which are known only when stabilised by ligands or in large spherical buckminster fullerine - like structures. Borazine, first prepared by Stock and Pohland in 1923, is a compound isoelectronic to benzene and is often called 'inorganic benzene'. Like benzene it is a 6 pi-electron, 6 membered ring which exhibits cyclic delocalisation, however not to such a great degree as in benzene. This reduction in delocalisation is due to the large difference in electronegativity between nitrogen and boron, compared to the carbon atoms which are all the same. The often trivalent Boron and Nitrogen have different bonding properties to tetrahederal Carbon but as one can see the resonance of borazine allows a strikingly similar bonding picture to that of benzene (although we know in reality these are not alternating single and double donds but six intermediaries between the two). However, it has been noted that the chemical properties of boarazine suggest little aromatic character, and the contrast between the chemical and physical properties of benzene and boarazine suggest that hybrid stuctures with both [HCCH] and [HNBH] moieties, of which there are 11 possible theoriesed molecules might exhibit a mixture of the properties of both. The most commonly examined hybrid is 1,2, azaborine. 1,2, Azaborine is reckoned commonly as being an intermediate of benzene and borazine with properties between those of borazine and benzene, and was initially very difficult to isolate. Of 1,2,3,4 Diazadiborine and 1,2,4,5 Diazadiborine, I have found nothing indicating their isolation, although they have been examined theoretically, in the forms shown here, and so by investigating properties across the 5 molecules I intend to observe whether these two molecules are similarly intermediary of benzene and borazine. The difficulty presented in the attempted isolation of these hybrids suggests that these compounds are reactive and chemically unstable.The aim of this part of the project is to compare these molecules by observing the structure, energies, charge distribution, vibrational and NMR spectra and molecular orbitals, and to see if there are any observable trends and whether the 3 intermediary compounds are true hybrids of benzene and borazine.

Part 5.3.1: Structural Analysis

The optimised benzene consists of 6 carbon atoms in a planar ring, each carbon with a single hydrogen atom bonded to it which are also planar to the molecule. The planarity is due to the delocalised pi systems above and below the plane and is a good indication of the said system being present. In a similar molecule like cyclohexane without the said system, the planarity is not observed and a chair conformation is achieved. The C-C-C and C-C-H bond angles are all 120 degrees, all C-H bond lengths are 1.08 angstroms and the C-C bond lengths are all 1.39 angstroms, between the lengths of a typical C-C single (1.47 angstroms) and C=C double(1.35 angstroms) bond. This is exactly in acordance with the literature.

For borazine, all the atoms are planar, suggesting a large degree of delocalisation of electron density above and below the ring. The B-N bond lengths are all 1.43 angstroms, the B-H bond lengths are all 1.19 angstroms and the N-H bond lengths are all 1.00 angstroms. The N-B-N bond angle is 117.0° and the B-N-B angle is 123.0°. It is interesting to see that the N-B-H and B-N-H bond angles are not the same, (122 and 118 degrees respectively). The electronegativity of boron and nitrogen differs from that of carbon and so it is unsurprising that the B-N bonds are a different length (longer due to overall increased electronegativity) to the C-C bonds. The N-H bond lengths are shorter than in benzene and the B-H longer due to the differing electronegativity. Nitrogen being more electronegative, pulls the hydrogen atom closer whilst boron is unable to pull it as close as carbon as it is less electronegative. The bond angles (internal) are quite close to 120 degrees and the alternation helps retain a strong degree of symmetry.

In 1,2-azaborine the B-N bond length is 1.44 angstroms, similar to the 1.43 angstroms in borazine, intermediate of a typical single and double B-N bond (1.51 and 1.31 angstroms respectively). This bond is of a very similar length to that in the literature, 1.43 angstroms. This suggests that there is some delocalisation of electron density on this bond, possibly from the nitrogen lone pair. The hydrogen to B/C/N bond lengths are equal to those of benzene and borazine and so are determined by the atom to which it is bonded and can be considered a typical single bond. There are two carbon-carbon bond lengths (1.37 and 1.42 angstroms(lit. 1.35 and 1.44 angstroms)), both of which are intermediary of a single and double bond, although one is much closer to the former and the other to the latter. Nonetheless, this indicates a degree of pi electron delocalisation. This confers some stability to the molecule. The N-C and N-B bond lengths are 1.37 and 1.51 angstroms respectively (lit. 1.36 and 1.52 angstroms). The B-N-C angle is 124 degrees and the N-B-C angle is 115 degrees. The latter angle is much less than the borazine and benzene angles. The C-C-C angles are 120 and 122 degrees very close to that of benzene. All the atoms of 1,2,azaborine are planar and this with the other properties indicate that 1,2 azaborine is intermediate of benzene and borazine and still retains some cyclic electron delocalisation.

In 1,2,3,4 diazadiborine the hydrogens are slightly out of the plane of the ring, the atoms of which are nearly totally planar, with a leverage of about 0.1 to 0.2 degrees. The H-C-C angles are 120 and 121 degrees with the B-C-H angle at 120 degrees and the N-C-H angle at 117 degrees. These are all quite close to 120 degrees and initially show promise as an intermediate. Also, all the internal ring angles are 120 degrees. The C-C bond length is 1.43 angstroms, close to that of a single bond, and the two distinct B-N bond lengths, 1.50 angstroms and 1.29 angstroms are descriptive of a single and double bond. This would insinuate a high degree of bond localisation despite the planarity.

In 1,2,4,5 diazadiborine the hydrogens are again, ever so slightly out of the plane of the ring, and the ring atoms are nearly totally planar. The C-N-B angles are 120 and 119 degrees and the C-B-N angles are 119 and 117 degrees. There is a large difference between the B-C-B angle and the N-C-N angle (117 and 127 degrees respectively). The nitrogen atom lone pairs repel and so the angle is greater. Both C-N bonds are 1.33 angstroms long despite the structure suggesting one being a single and one double bond, suggesting delocalisation along the N-C-N. The N-B and B-C bonds show two distinct lengths (1.29 and 1.50 angstroms, and 1.37 and 1.59 angstroms respectively) suggesting a distinct alternation of single and double bonds and lack of delocalisation of the N-B-C-B-N region. This partial delocalisation is interesting and suggests not an intermediary of benzene and borazine but a half breed between aromatic and non aromatic.

Part 5.3.2: IR Frequencies

Notable Selected IR Frequencies

Reference Number	Benzene	Benzene Frequency /cm-1	Borazine	Borazine Frequency /cm-1	1,2,3,4 Diazadiborine	1,2,3,4 Diazadiborine Frequency /cm-1	1,2,4,5 Diazadiborine	1,2,4,5 Diazadiborine Frequency /cm-1	1,2 Azaborine	1,2 Azaborine Frequency /cm-1
1		688 (Intensity 111)		856 (Intensity 0)		488 (Intensity 1)		359 (Intensity 2)		758 (Intensity 8)
2		1013 (Intensity 0)		942 (Intensity 0)		958 (Intensity 2)		467 (Intensity 0)		894 (Intensity 4)
3		1060 (Intensity 5)		951 (Intensity 0)		982 (Intensity 2)		613 (Intensity 6)		909 (Intensity 0)
4		1512 (Intensity 9)		1000 (Intensity 273)		1695 (Intensity 333)		1019 (Intensity 1)		978 (Intensity 6)
5		3180 (Intensity 44)		2761 (Intensity 0)		3124 (Intensity 16)		1277 (Intensity 29)		1000 (Intensity 0)
6		3180 (Intensity 44)		3251 (Intensity 0)		3270 (Intensity 0)		1695 (Intensity 344)		1100 (Intensity 16)
IRs	Benzene		Borazine		1,2,3,4 Diazadiborine		1,2,4,5 Diazadiborine		1,2 Azaborine

For all the examined molecules there are a great number of vibrations, (ranging from 18 to 30!), and so only the most notable and interesting ones are listed here. These vibrations include contractions of the entire ring and so one would expect similar vibrations in all the molecules.

Whilst benzene has a large number of zero intensiy vibrations due to its high symmetry the other molecules have more as they have less symmetry, especially the diazadiborines. I have selected a few vibrations to show in the table. The vibrations of the diazadiborines are quite different to those of the other molecules, as they are structurally quite different, with not all atoms vibrating at the same time like in the other molecules. Not a great deal about the electronics can be determined on sole observation of the stretching frequencies, compared to the other analyses, but they are interesting nonetheless.

Borazine, azaborine and benzene have relatively similar motions. For the known compounds we can compare some stretches with the literature. to check we have the compounds correctly optimised. The calculated frequencies will be a little off the experimental as Gaussian tends to overestimate the stretching frequencies and the higher frequency modes.The literature gives, for borazine, a B-N stretch for 1465 - 1330 cm^-1 (calculated 1526,1392 cm^-1)and a B-N stretch for 1,2 azaborine at 1613, 1533 , 1453 , 1427 and 1350 cm^-1 (calculated 1629, 1560, 1486, 1392 and 1242cm^-1 ). The literature and calculations match quite well. The 1,2 azaborine B-N stretches are at a higher frequency than those for borazine, suggesting a stronger bond despite the similar bond lengths. This can be interpreted to mean an increased degree of aromatic stability in 1,2 azaborine comparative to borazine, as suggested in the literature. 1,2 Azaborine has more C-H stretches than benzene in the 3000-3200 region which suggests a far greater non equivalence of the azaborine hydrogens. The 1,2 azaborine C=C stretches are at 1625 and 1560 cm^-1, benzene at 1512 cm^-1. That 1,2 azaborine has more C=C stretches suggests more non degeneracy than in benzene.

The diazadiborines do not have more than one C=C double bond but have a greater number of B-N bonds and so are better compared to borazine which has B-N stretches at 1526 and 1392 cm^-1. Both of these diazadiborines, along with borazine, show two distinct B-N stretches (1,2,3,4 diazadiborine, 1695, 1592 cm^-1 ; 1,2,4,5 diazadiborine, 1695, 1505 cm^-1) suggesting non equivalent single and double B-N bonds.

Part 5.3.3: Molecular Orbitals And Charge Distribution

Molecular Orbitals

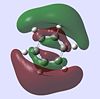
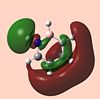
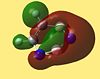
Molecule	HOMO - 4	HOMO - 3	HOMO - 2	HOMO - 1	HOMO	LUMO	LUMO +1	LUMO +2	LUMO +3	LUMO +4
Benzene
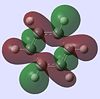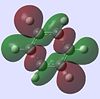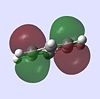1,2, Azaborine
1,2,3,4 Diazadiborine
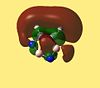
1,2,4,5 Diazadiborine
Borazine

The molecular orbitals provide some of the most interesting information about these molecules. In benzene there are delocalised pi clouds above and beneath the plane of the ring, bringing great stability to the molecule. This cloud of circular delocalisation is best visualised in the HOMO-4 , LUMO +2 , LUMO +3 and LUMO+4 orbitals where one can clearly see the circular patterns of electron density. As benzene comprises totally of equal atoms the majority of orbitals are entirely C₂ symmetric. This is not so for the other molecules where heteroatoms distort the orbitals. The benzene and borazine orbitals are very similar, though more distorted in borazine, with the orbital lobes having different sizes on account of the boron-nitrogen electronegativity difference.

HOMO -5 Molecular Orbitals

1,2,3,4 Diazadiborine	1,2,4,5 Diazadiborine

The LUMO+2 of 1,2 Azaborine is disconnectred unlike that for benzene and borazine. Despite this 1,2 Azaborine is known to show greater aromaticity than borazine. This MO therefore is most likely to show the regions where the delocalised electron density are greatest, at the nitrogens in borazine and around the carbons in 1,2 azaborine. The LUMO+2 for the diazadiborines is not similar at all and so it is harder to analyse it in the same manner. The LUMO+3 and +4 are very interesting orbitals across the series. For benzene they show great symmetry all about the molecule, descriptive of the aromaticity about the entire ring. The lobes are more skewed in the other molecules indicative of the lesser degree of electron delocalisation. The LUMO+4 of the diazadiborines show that there is at least partial delocalisation even though it doesnt appear to span the whole molecule. The HOMO-4 for borazine still shows evidence of a cyclic delocalised pi-electron cloud indicative of an aromatic system. In borazine the cloud is not fully circular but more triangular showing parts of the ring, specifically the nitrogen components harbour more of the electron density about them. This makes the system not perfectly aromatic but multiply polar. This is in accordance with the literature which states the aromatic stabilised energy for borazine is half that of benzene. The HOMO-4 for 1,2 azaborine retains a more fully circular character than that for borazine. As can be seen in the higher LUMO orbitals the lobes are primarily centred around the carbons where most of the aromaticity is centred. The HOMO's of all 5 molecules look remarkably similar, as do the LUMO+1, but generally the orbitals of the diazadiborines are much distorted compared to the others. The HOMO-4 which is usually descriptive of the cyclic delocalisation of these aromatic compounds, is not. The HOMO-5 however, is. One might expect these compounds therefore to show some aromaticity but all things considered, less than the other 3 compounds.

Charge Distribution

Molecule	Charge Distribution	Colour Coded Charge Distribution	Molecule	Charge Distribution	Colour Coded Charge Distribution
Benzene			1, 2 Azaborine
1, 2, 3, 4 Diazadiborine			1, 2, 4, 5 Diazadiborine
Borazine			Oh what can ail thee, knight-at-arms, Alone and palely loitering? The sedge has withered from the lake, And no birds sing.	Oh what can ail thee , knight-at-arms, So haggard and so woe-begone? The squirrel's granary is full,And the harvest's done.	I see a lily on thy brow, With anguish moist and fever-dew,And on thy cheeks a fading rose Fast withereth too. La Belle Dame Sans Merci - John Keats

In the coloured charge distribution representations, luminescent green is indicative of a high positive charge and bright red of a high negative charge. Black is indicative of a neutral charge. The charge distribution for benzene is much as expected with equal charge on all carbon atoms which are negative due to the electron delocalisation, and equal and opposite positive charge on all the hydrogens. In the borazine ring there is an alternating positive and negative charge distribution as expected from boron and nitrogen due to the great difference in electronegativity. Hydrogens bonded to the nitgrogens have a positve charge and the opposite is true for those attached to boron. The hydrogen-ring atom pairs do not cancel out exactly in charge but each H-B-N-H group adds to zero. It is interesting to note that the hydrogens attached to boron have only a very low negative charge and are nearly neutral. I imagine this is due to hydrogen's aversion to be negatively charged. Both benzene and borazine have an overall zero charge.

In 1,2-azaborine, the H atom connected to the N atom has a positive charge as does the hydrogen attached to the carbon adjacent to the nitrogen. As this carbon is also positively charged it is evident that there are two atoms of positive charge adjacent to one another. This is likely to cause repulsion between the two atoms and so this hydrogen, and that attached to the nitrogen are likely to be susceptible to easy removal and protic. The boron is more positively charged than in borazine and 3 of the 4 carbons, especially the one adjacent to the boron and the one adjacent to the positively charged carbon, have quite considerable negative charge, greater even than in benzene. These varied charges mean that certain regions are more prone to certain attacks than others, the positive areas to nucleophilic attack and the more negative regions to electrophilic attack. In general, a molecule such as this with varied potential for reaction is very reactive and may contribute to why 1,2 azaborine is reputedly unstable.

The diazadiborines also have very varied charge distribution. In both diborines, one carbon has a positive and one a negative charge and all hydrogens have a slight positive charge. The nitrogens are as always negatively charged, the borons positively. The varied charge distribution, like in 1,2 azaborine suggests a mixture of potential reactivity so these molecules are likely to be even more reactive, contributing to the difficulty in their isolation.

Part 5.3.4: NMR

Multiple Benzene NMR (inc. 13C)	Multiple 1,2,Azaborine NMR (inc. 13C)	Multiple 1,2,3,4,Diazadiborine NMR (inc. 13C)	Multiple 1,2,4,5,Diazadiborine NMR (inc. 13C)	Multiple Borazine NMR

All NMR are quoted in ppm and are of the relevant atom NMR (¹H ,¹³C ,¹¹B ,^14/15N ,²⁹Si ,³¹P). It is worth noting that it is the shielding calculated here as the DFT calculations did not work.

In benzene, as one would expect, all hydrogens are shown equivalent, and all carbons are shown as equivalent. The carbons are at 55 ppm and the hydrogens are at 24 ppm. 24 ppm is rather high for protons on an aromatic ring, usually they are at about 7 ppm (lit 7.2ppm). This is something I have come across before when trying to predict NMR, that the hydrogen shifts are unusually large. Comparatively, the shift for benzene is too small, as it is usually 128.5 ppm.

Borazine comprises of 3 equivalent nitrogen atoms (120 ppm, lit. 373PPM), 3 equivalent boron atoms (77 ppm, Lit.22 ppm) and two types of hydrogen atoms, those attached to nitrogen (25 ppm) and those attached to boron (27 ppm). The hydrogen NMR here is flawed compared to the literature which says the boron hydrogens are at 4.4ppm and the nitrogen hydrogens at 5.6ppm, which makes more sense than them being the other way around.

For 1,2 Azaborine the H shifts are far too high again, between 22 and 27 ppm when the literature places the shifts at 4 to 9 ppm. The literature places the H nmr peaks in the opposite order to those discovered here (N-H, 22.6 ppm, C-H (opposite to N), 23.4 ppm, C-H (next to N), 23.6 ppm, C-H (next to B), 24.3ppm, C-H (opposite to B), 24.6 ppm, B-H, 26.7 ppm). The C NMR shows 4 distinct peaks for 4 distinct carbons, the C opposite N at 35 ppm, the C next to N at 41 ppm, the C next to B at 51 ppm and the C opposite B at 67 ppm. The N appears a 72 ppm and B at 11 ppm on their respective spectra.

The diazadiborines have been assigned thus. 1,2,3,4 Diazadiborine (respective shielding spectra); C (next to N) -2ppm, C (next to B) 105 ppm, N (B-N-B) 59 ppm, N (C-N-B) 65 ppm, B (C-B-N) 62 ppm, B (N-B-N) 73 ppm, H-CN 23 ppm, N-CB 27 ppm. 1,2,4,5 Diazadiborine (respective shielding spectra); The N's (13 ppm) and the B's (57 ppm) are eqivalent, C (N-C-N) 20 ppm, C (B-C-B) 133 ppm, H (H-CN) 24 ppm, H (H-CB) 28 ppm.

I am fairly certain that the values calculated here are related to the usual NMR but tend to predict the reverse assignments, high values appearing low and vice versa. This makes sense given the assignments made. It is a shame the DFT calculations did not work.

Part 5.3.5: NBO Analysis

NBO Analysis

Benzene	Benzene	Benzene	Borazine	Borazine	Borazine	1,2, Azaborine	1,2, Azaborine	1,2,Azaborine	1,2,3,4 Diaza diborine	1,2,3,4 Diaza diborine	1,2,3,4 Diaza diborine	1,2,4,5 Diaza diborine	1,2,4,5 Diaza diborine	1,2,4,5 Diaza diborine
Bond	Atomic Contribution	Orbital Contribution	Bond	Atomic Contribution	Orbital Contribution	Bond	Atomic Contribution	Orbital Contribution	Bond	Atomic Contribution	Orbital Contribution	Bond	Atomic Contribution	Orbital Contribution
C-C	50% from C; 50% from C	C:36.09%(s), 63.87%(p), 0.04%(d);C: 36.09%(s), 63.87%(p), 0.04%(d)	B-N	75.76% from N; 24.24% from B	N:39.51%(s), 60.46%(p), 0.03%(d);B: 31.44%(s), 68.42%(p), 0.14%(d)	C-C	50.55% from C; 49.45% from C	C: 35.59%(s), 64.37%(p), 0.04%(d); C: 34.17%(s), 65.78%(p), 0.05%(d)	C-C	51.51% from C; 48.49% from C	C: 34.40%(s), 65.54%(p), 0.05%(d); C: 39.84%(s), 60.11%(p), 0.05%(d)	(N)C-H	64.00% from C; 36.00% from H	C: 35.70%(s), 64.20%(p), 0.01%(d); H: 99.95%(s), 0.05%(p)
C-H	60.12% from C; 39.88% from H	C: 27.79%(s), 72.16%(p), 0.05%(d);H: 99.95%(s), 0.05%(p)	B-H	45.18% from B; 54.82% from H	B: 37.21%(s), 62.75%(p), 0.04%(d);H: 99.92%(s), 0.08%(p)	C-C	46.91% from C; 53.09% from C	C: 0.00%(s), 99.95%(p), 0.05%(d); C: 0.00%(s), 99.96%(p), 0.04%(d)	C-B	64.28% from C; 35.72% from B	C:33.03%(s), 66.92%(p), 0.05%(d);B: 55.78%(s), 44.19%(p), 0.03%(d)	(B)C-H	59.57% from C; 40.43% from H	C: 30.81%(s), 69.13%(p), 0.06%(d); H: 99.94%(s), 0.06%(p)
My heart aches, and a drowsy numbness pains	My sense, as though of hemlock I had drunk,	Or emptied some dull opiate to the drains	N-H	70.28% from N; 29.72% from H	N: 20.89%(s), 79.06%(p), 0.04%(d);H: 99.93%(s), 0.07%(p)	C-C	50.02% from C; 49.98% from C	C: 40.91%(s), 59.05%(p), 0.04%(d); C: 36.11%(s), 63.84%(p), 0.05%(d)	C-N	40.27% from C; 59.73% from N	N:34.26%(s), 65.65%(p), 0.09%(d);C: 31.58%(s), 68.31%(p), 0.11%(d)	C-N	39.24% from C; 60.76% from N	N:34.79%(s), 65.12%(p), 0.08%(d);C: 34.69%(s), 65.20%(p), 0.11%(d)
One minute past, and Lethe-wards had sunk:	'Tis not through envy of thy happy lot,	But being too happy in thine happiness,	That thou, light-wingèd Dryad of the trees,	In some melodious plot Of beechen green, and	shadows numberless, Singest of summer in full-throated ease.	C-N	37.703% from C; 62.30% from N	C: 29.13%(s), 70.76%(p), 0.11%(d); N: 33.34%(s), 66.62%(p), 0.05%(d)	(C)N-B	25.91% from B; 74.09% from N	B: 49.60%(s), 50.33%(p), 0.08%(d); N: 28.70%(s), 71.00%(p), 0.30%(d)	N-B	26.69% from B; 73.31% from N	B: 44.76%(s), 53.13%(p), 0.11%(d); N: 42.88%(s), 57.04%(p), 0.08%(d)
O for a draught of vintage! that hath been	Cool'd a long age in the deep-delvèd earth,	Tasting of Flora and the country-green,	Dance, and Provençal song, and sunburnt mirth!	O for a beaker full of the warm South!	Full of the true, the blushful Hippocrene,	C-B	65.18% from C; 34.82% from B	C: 38.37%(s), 61.60%(p), 0.03%(d); B: 36.73%(s), 63.24%(p), 0.04%(d)	(C)B-N	25.56% from B; 74.44% from N	B: 44.05%(s), 55.87%(p), 0.08%(d); N: 36.35%(s), 63.37%(p), 0.28%(d)	B-C	66.80% from C; 33.20% from B	B: 55.08%(s), 44.88%(p), 0.04%(d); C: 32.02%(s), 67.92%(p), 0.06%(d)
With beaded bubbles winking at the brim,	And purple-stainèd mouth;	That I might drink, and leave the world unseen,	And with thee fade away into the forest dim:	Fade far away, dissolve, and quite forget	What thou among the leaves hast never known,	B-N	23.31% from B; 76.69% from N	B: 27.54%(s), 72.30%(p), 0.15%(d); N: 42.79%(s), 57.19%(p), 0.02%(d)	(B)C-H	62.16% from C; 37.84% from H	C: 32.45%(s), 67.52%(p), 0.03%(d); H: 99.95%(s), 0.05%(p)
The weariness, the fever, and the fret	Here, where men sit and hear each other groan;	Where palsy shakes a few, sad, last grey hairs,	Where youth grows pale, and spectre-thin, and dies;	Where but to think is to be full of sorrow	And leaden-eyed despairs;	B-N	14.54% from B; 85.46% from N	B: 0%(s), 99.79%(p), 0.21%(d); N: 0%(s), 100%(p)	(N)C-H	59.96% from C; 40.04% from H	C: 28.62%(s), 71.33%(p), 0.06%(d); H: 99.95%(s), 0.05%(p)
Where beauty cannot keep her lustrous eyes,	Or new Love pine at them beyond to-morrow.	Away! away! for I will fly to thee,	Not charioted by Bacchus and his pards,	But on the viewless wings of Poesy,	Though the dull brain perplexes and retards:	N-H	70.31% from N; 29.69% from H	N: 21.84%(s), 78.11%(p), 0.05%(d); H: 99.92%(s), 0.08%(p)
Already with thee! tender is the night,	And haply the Queen-Moon is on her throne,	Cluster'd around by all her starry Fays	But here there is no light,	Save what from heaven is with the breezes blown	Through verdurous glooms and winding mossy ways.	B-H	46.10% from B; 53.90% from H	B: 35.79%(s), 64.36%(p), 0.04%(d); H: 99.92%(s), 0.08%(p)		Ode To A Nightingale -	John Keats

As these molecules are not isomers and comprise of different amounts of different atoms the energies cannot be compared with great certainty but they are all quite similar, being -232 a.u. (benzene), -243 a.u (borazine), -236 a.u (1,2,azaborine), -237a.u (both diazadiborines). Benzene and borazine have dipole moments of 0.00 Debye whilst 1,2,azaborine has a dipole moment of 2.16 debye, 1,2,3,4 diazadiborine has a dipole moment of 1.81 debye and 2.20 debye for 1,2,4,5 diazadiborine. Generally there is a very low d orbital contribution from these molecules. There are pi interactions in all molecules, even the diazadiborines across the B-N bonds indicating some delcoalisation. 1,2,azaborine exhibits more of this than the diazadiborines. In many cases there is a roughly even contribution from each atom except where a nitrogen ( very electronegative) is bonded to a B or a H (very electropositive) in which case the nitrogen contributes considerably more. This is to be expected.

Part 5.3.6: Conclusion

With special consideration with regards to the molecular orbitals and all other data considered, one can see that 1,2 azaborine definitely exhibits a good deal of delocalisation, between that of benzene and borazine, and can certainly be considered an intermediary of the two, though its mixed charge distribution is likely to cause it to react very readily and render it unstable. This latter point is true of the diazadiborines. They have some delocalised character, as seen by the HOMO-5 orbitals, but this is to a much lesser extent than in the other molecules, though 1,2,3,4 diazadiborine shows more aromatic promise than 1,2,4,5 diazadiborine as the adjacent carbon molecules are able to help effect a more benzene-like delocalisation. Were there more time I would have liked to investigate more molecules of this kind to see if any other azaborine type ring structures exhibit aromaticity like 1,2 azaborine, benzene and (to a lesser degree) borazine, and whether any of these are likely to be at all more stable.

Part 5.4: Replacing An Atom

Substituted Benzene

Substituted Borazine

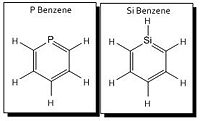
In this section of the project I intend to investigate the effect of substituting an atom of the known compounds benzene and borazine. Both these compounds exhibit cyclic delocalisation which may be affected by a substitution. Silicon and Phosphorous atoms will be substituted into these compounds (for borazine, they will be substituted on both the nitrogen and boron positions). Silicon has the same number of valence electrons as carbon, as phosphorous does with nitrogen so the the insertion of Si into benzene is expected to have less of an effect as the insertion of a P atom, likewise, the substitution of a P atom for an N in borazine is expected to have less of an effect than the other possible substitutions, nonetheless, the altering of the number of valence electrons will be interesting. Si benzene and P benzene, often called silabenzene and phosphabenzene, are known compounds, with the P analogue being considerably more stable and known to exhibit aromaticity. The borazine equivalents however are unknown and no reference to them could be found on the beilstein/gmelin databases, even in kinetically stabilised forms.

Part 5.4.1: Structural Analysis

The structures of benzene and borazine have already been commented upon in the previous component of this project. Next our attentions turn to the substituted versions. The benzene structures have been optimised with alternating single and double bonds, with the valencies regarding the number of hydrogen atoms attached varied accordingly. The borazine structures have been optimised all with single bonds as per the uncharged state of borazine. Again the number of hydrogens per atom have been adjusted accordingly to satisfy valence demands.

In order to preserve the valency of phosphorous it is without a H atom attached. The atoms nonetheless are still planar and all C-C bonds are 1.39 angstroms long, intermediate of a single and double bond, and the P-C bonds are 1.74 angstroms long. The optimised structure suggests aromaticity about the carbons but not the phosphorous, unsurprising as the phosphorous atom does not have an equal valency to carbon and may not be able to delocalise an electron.

Si Benzene has the majority of atoms planar to c. 1 or 2 degrees. The C-Si bonds are long, at 1.77 angstroms each, but this equality of length stands against the notion of a Si-C single and Si=C double bond but two bonds of equal length. All C-C bonds are 1.40 angstroms long, intermediate of a single and double bond and suggests that despite the replacement that delocalisation is retained. The Si-H bond is larger than the C-H bonds but this is to be expected as Silicon is a larger atom.

The Si substituted borazine (replacing boron) is still totally planar, with exception of the Si Hydrogens (Si has two as the valency of Si must be preserved) and all B-N bonds are 1.43 angstroms. This suggests delocalisation about the boron and nitrogen atoms as this length is intermediate of boron-nitrogen single and double bonds. The Si-N bonds are both 1.74 angstroms. Both N-B-N angles are 120 degrees, the B-N-B angle is 126 degrees, both B-N-Si angles are 125 degrees and the N-Si-N angle is 103 degrees.

The Si substituted borazine (replacing nitrogen) is still totally planar, with exception of the Si Hydrogens. All B-N bonds are 1.43 angstroms, as are the two Si-B bonds. This suggests delocalisation about the whole ring as this length is intermediate of boron-nitrogen single and double bonds. Both B-N-B angles are 123 degrees, the N-B-N angle is 117 degrees as are both N-B-Si angles. The B-Si-B angle is 123 degrees. These are all reasonably close to 120 degrees. The considerably out-of-plane Si hydrogens are likely to affect the system and may hinder aromaticity about the ring.

The P substituted borazine (replacing boron) is almost completely planar. The B-N bonds closest to to P are 1.41 angstroms long and those furthest are 1.44 angstroms. This non equivalence is not initially suggesive of delocalisation however the lengths are intermediate of boron-nitrogen single and double bonds. The P-N bonds are both 1.73 angstroms. Both N-B-N angles are 121 degrees, the B-N-B angle is 127 degrees, both B-N-P angle are 122 degrees and the N-P-N angle is 107 degrees.

The P substituted borazine (replacing nitrogen) is still planar and all B-N bonds are 1.43 angstroms long. The two P-B bonds are 1.85 angstroms long. This suggests delocalisation about the borons and nitrogens however the P-B bond does seem rather long. Both B-N-B bonds are 130 degrees, the N-B-N bond is 122 degrees, both N-B-P angles are 113 degrees. The B-P-B angle is 111 degrees. There certainly seems to be some delcoalisation.

The Si substituted borazine (replacing nitrogen) seems to be the most likely candidate for retention of aromatic behaviour at a first glance.

Part 5.4.2: IR Frequencies

For all the examined molecules there are a great number of vibrations and so only the most notable and interesting ones are listed here.

The IR vibrations for the ring atoms are very similar across the series and the frequency ranges for certain vibrations are similar across the series. In general, there is a great deal of consistency, unsurprising as only an atom at a time has been changed.

Notable Selected IR Frequencies

Ref. No.	Benzene	Benzene Frequency /cm-1	P Benzene	P Benzene Frequency /cm-1	Si Benzene	Si Benzene Frequency /cm-1	Borazine	Borazine Frequency /cm-1	P Rep N Borazine	P Rep N Borazine Frequency /cm-1	Si Rep N Borazine	Si Rep N Borazine Frequency /cm-1	P Rep B Borazine	P Rep B Borazine Frequency /cm-1	Si Rep B Borazine	Si Rep B Borazine Frequency /cm-1
1		688 (Intensity 111)1		470 (Intensity 4)		429 (Intensity 11)		856 (Intensity 0)		631 (Intensity 33)		630 (Intensity 45)		187 (Intensity 0)		325 (Intensity 9)
2		1013 (Intensity 0)		710 (Intensity 65)		714 (Intensity 68)		942 (Intensity 0)		753 (Intensity 3)		682 (Intensity 0)		944 (Intensity 0)		813 (Intensity 83)
3		1060 (Intensity 5)		766 (Intensity 0)		768 (Intensity 2)		951 (Intensity 0)		896 (Intensity 0)		855 (Intensity 0)		1163 (Intensity 10)		925 (Intensity 4)
4		1512 (Intensity 9)		1016 (Intensity 1)		972 (Intensity 1)		1000 (Intensity 273)		2619 (Intensity 137)		887 (Intensity 4)		1396 (Intensity 221)		982 (Intensity 15)
5		3180 (Intensity 44)		1211 (Intensity 0)		1084 (Intensity 4)		2761 (Intensity 0)		3623 (Intensity 10)		2602 (Intensity 92)		2624 (Intensity 60)		1391 (Intensity 141)
6		3180 (Intensity 44)		3177 (Intensity 20)		3175 (Intensity 8)		3251 (Intensity 0)		3624 (Intensity 53)		3607 (Intensity 2)		3635 (Intensity 35)		2620 (Intensity 124)
IR	Benzene		P Benzene		Si Benzene		Borazine		Borazine N P Rep		Borazine N Si Rep		Borazine B P Rep		Borazine B Si Rep

Part 5.4.3: Molecular Orbitals And Charge Distribution

Molecular Orbitals

Molecule	HOMO - 4	HOMO - 3	HOMO - 2	HOMO - 1	HOMO	LUMO	LUMO +1	LUMO +2	LUMO +3	LUMO +4
Benzene
Si Benzene
P Benzene
Borazine
Si (Rep N) Borazine
P (Rep N) Borazine
Si (Rep B) Borazine
P (Rep B) Borazine

Both Si and P benzene show promise for aromaticity with the tell-tale double ring structure in the HOMO-4 with P Benzene mirroring the LUMO+2 LUMO+3 and LUMO+4 of benzene closely also. The LUMO+4 of Si benzene seems to be the mirror of the LUMO+2 of benzene. Both the P and Si benzene equivalents have the ring broken at this point at the heteroatom, but as we have seen in 1,2 azaborine, this is not neccessarily an indicator of non-aromaticity. The inner ring of the P benzene is nearly complete however which is a promising sign. The HOMO and LUMO of P benzene are its pi and pi* orbitals with the lone pair in the HOMO. Thus this molecule can act as a sigma acceptor and pi donor ligand.

HOMO -5 Molecular Orbitals

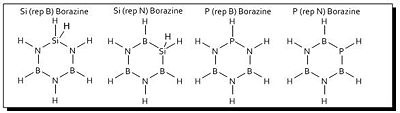
Borazine P (B Rep)	Borazine Si (B Rep)

HOMO -6 Molecular Orbital

Borazine Si (N Rep)

Of the substituted borazines, P (Rep N) Borazine is encouraging, and in fact, the LUMO+2 bears more resemblance to that of benzene than borazine. It would be interesting to see the experimental details of this molecule if it is ever synthesised. The over molecules, however, would, I imagine exhibit very low delocalisation, especially Si (Rep N) Borazine where the delocalised cloud is as low as the HOMO-6 and is very distorted over the out-of-plane hydrogens. The symmetry breaking of the introductions leads to some very irregular looking molecular orbitals such as the LUMO+3 and +4 of Si (Rep B) Borazine.

Charge Distribution

Molecule	Charge Distribution	Colour Coded Charge Distribution	Molecule	Charge Distribution	Colour Coded Charge Distribution	Molecule	Charge Distribution	Colour Coded Charge Distribution	Molecule	Charge Distribution	Colour Coded Charge Distribution
Benzene			Si Benzene			P Benzene			Borazine
Si Rep N Borazine			P Rep N Borazine			Si Rep B Borazine			P Rep B Borazine

For the most part, the atom replacements do not have a very drastic effect on the charge distribution, that is to say that no red area is now green or vice versa (with the exception of the replaced atoms themselves), but there are a great deal more neutral areas. The benzene substitutions lead to the carbons adjacent to the heteroatom being considerably more negative than the others, and so to here would an electrophilic attack be made. A nucleophilic attack would probably go to the heteroatom as they show a more positive charge than the hydrogens. Despite the aromaticity being somewhat preserved, the substitution has changed the potential reactivity of the compounds, and Si benzene indeed is, as a result, very hard to isolate (P Benzene is easier to isolate due to the similar electronegativities of P and C thus rendering less change on the molecule and allowing it to retain its stability). The bond in Si benzene ( C-Si) is very polar and so quite easy to break as Si is not very capable of forming pi bonds to C.

The borazine analogues seem to have undergone relatively little charge distribution alterations. The most notable is for Si and P Rep N borazine where there are now three electropositive atoms next to one another. This is more of an issue for Si rep N and may contribute to the loss of aromaticity. The B replacements have a very similar distribution to borazine.

Part 5.4.4: NMR

I shall not go into detail here as the important thing is the non equivalence induced by the addition of the substituted atom which can clearly be seen. The same notes apply as before, each atom is listed under its own NMR and it is the shielding here recorded in ppm as the GIAO method was employed (as the DFT methods failed repeatedly). A link to a summary of the NMR is given also. The assignments going from 0 -> infinity are in the opposite direction to that which a normal NMR, i.e from the literature, would state. This is only relevant within an atom group, i.e for all carbon assignments.

Multiple P Benzene NMR (inc. 13C)	Multiple Si Benzene NMR (inc. 13C)	Multiple P Rep N Borazine NMR	Multiple Si Rep N Borazine NMR	Multiple P Rep B Borazine NMR	Multiple Si Rep B Borazine NMR
P Benzene Summary	Si Benzene Summary	Borazine N P Rep Summary	Borazine N Si Rep Summary	Borazine B P Rep Summary	Borazine B Si Rep Summary

Part 5.4.5: Conclusion

In conclusion, I would be most interested in looking into the synthesis of P Rep N borazine to examine if experimentally it shows aromaticity as expected. In general, the atom substitution seems to break the aromaticity to a degree, but that said, P Benzene is known to enjoy 88% of the aromaticity of benzene and so it is not impossible that other such compounds exist.

Part 5.5: Conclusion

In conclusion I am very happy with the work I have undertaken and it has been interesting to look at various ways of obtaining semi-aromatic compounds. It has been interesting also to look at compounds of which there is no record of synthesis, such as the borazine analogues, and to predict what kind of properties they may have.

Part 5.6: Published Files

Optimisations (DFT, B3LYP, 6-311G(d,p)) were run on the provided laptop and so are not presented here.

Part 5.6.1: Frequencies/MOs

Benzene 1,2 Azaborine 1,2,3,4 Diazadiborine 1,2,4,5 Diazadiborine Borazine P (replacing C) Benzene Si (replacing C) Benzene P (replacing B) Borazine Si (replacing B) Borazine P (replacing N) Borazine Si (replacing N) Borazine

Part 5.6.2: GIAO NMRs (d-DCM Solvent)

Benzene 1,2 Azaborine 1,2,3,4 Diazadiborine 1,2,4,5 Diazadiborine Borazine P (replacing C) Benzene Si (replacing C) Benzene P (replacing B) Borazine Si (replacing B) Borazine P (replacing N) Borazine Si (replacing N) Borazine