Module 2

This module involves using the program Gaussian to model inorganic molecules. The aim of this course is to become more familiar in how the program works by increased understanding for example of how one can use different pseudo potentials and basis sets when optimizing a molecule.

Modelling a molecule of BH₃

This section of the course involves the modelling of a molecule of BH₃ and then using tools within Gaussian to study it.

Optimizing a molecule of BH₃

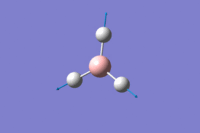
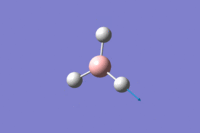
Firstly a trigonal planar molecule of BH₃ was created using Gaussview. The bond lengths were manually set to 1.5A^o. The molecule of BH3 was then optimized using the method B3LYP and the basis set 3-21G and the calculation type was set to optimization. The summary table for the optization can be seen below to the right.

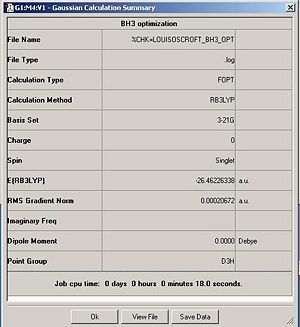
The optimized bond angle was found to be 1.19A^o. The H-B-H bond angle was 120 degrees.

The graphs below show how the gradient and energy changed over the course of the optimization.

Both the graphs show the same relationship, as the number of optimization steps increases the total energy and gradient decrease. The gradient decreases to around zero and this is expected as the lowest energy configuration will be when the gradient equals zero as this is a minima. A gradient is defined as the rate of change of a physical quantity or dimension.

Molecular Orbitals of BH₃

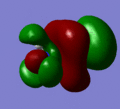
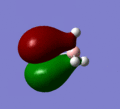
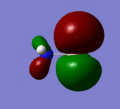
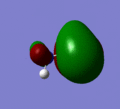
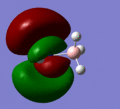
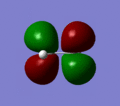
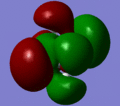
The molecular orbitals of BH₃ were computed using the optimized form of the molecule and the calculation type was set to energy, the basis set to to 3-21g and under the NBO tab, full NBO was selected as well as the words "pop=full" were added to the additional keywords section. The first eight molecular orbitals of BH₃ can be seen in the gallery below.

MO 1
MO 2
MO 3
MO 4
MO 5
MO 6
MO 7
MO 8

NBO ANALYSIS

The images corresponding to the NBO analysis are shown below. The first image shows the atoms coloured by charge, with the bright green boron having a high positive charge and the dark red hydrogens having a negative charge. The second image shows the atoms "NBO charge".

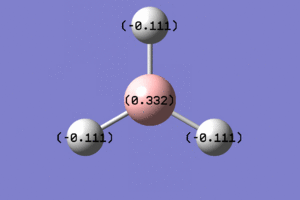https://www.ch.imperial.ac.uk/wiki/images/a/ae/%25CHK%3DLOUISOSCROFT_BH3_POP.LOG

Vibrational Analysis

A frequency calculation was then carried out on the optimized BH₃. The basis set used was 3-21g, corresponding to the level used for the original optimization and the additional keywords added were "pop=(full,nbo)". The frequency summary table can be seen below. The frequency analysis was carried out on the correct molecule because the frequency summary energy matches the summary energy for the optimization, which is shown earlier.

The six vibrations were then animated and recorded in the table below.

Table of bH₃ Vibrations
No.	Mode	Frequency/cm^-1	Intensity (IR)	Symmetry D_3h point group
1	B-H wagging	1144	92	A2"
2	H-B-H scissoring	1203	12	E'
3	H-B-H rocking	1203	12	E'
4	B-H symmetric stretch	2598	0	A1'
5	B-H asymmetric stretch	2737	103	E'
6	B-H asymmetric stretch	2737	103	E'

The IR spectrum was also produced:

Even though there are six modes of vibration only three peaks are observed in the IR spectrum and this is due to one of the vibrations (vibration 4) having an intensity of zero and so is not observed. The other reason is that vibrations 2 and 3 are degenerate as well as vibrations 5 and 6. They are degenerate because they occur at the same frequency. This therefore leads to only three observable peaks.

The MO diagram of BH₃

Comparison of Computed orbitals and LCAO representations
Orbital	Computed Molecular orbital	LCAO representation
MO 1
MO 2
MO 3
MO 4
MO 5
MO 6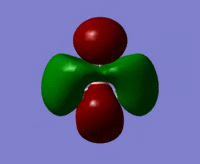
MO 7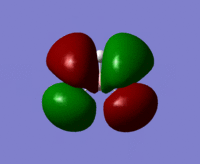
MO 8

Pleaae note that the LCAO representations need to be rotated by 180 degrees (apart from the first one) to match up properly with the orientations of the computed molecular orbitals.

From the above table it can be seen that the computed orbitals match up well with the LCAO representations. The only real difference is that the LCAO representations give a better view of the contributions from individual orbitals whereas the computed orbital diagrams merge the orbitals together. This therefore shows that the LCAO method is good for approximating molecular orbitals. Qualitative MO theory is good for determining the position of molecular orbitals in an MO diagram in terms of energy but it is more accurate to look at the actual energies of the molecular orbitals which is possible when they have been modelled using Gaussian.

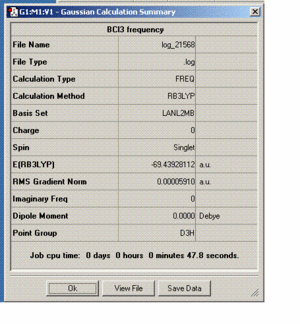
BCl₃ Optimization

The method used was B3LYP and the basis set used was LanL2MB. The same method and basis set must be used for an optimization and a frequency analysis so that an accurate result is produced as a certain method and basis set has set parameters and if these are mixed then the calculation will fail. A frequency analysis needs to be carried out to make sure that the form of the molecule you have is the fully optimized version as otherwise you need to repeat the optimization. A fully optimized molecule is one that has the lowest potential energy and this is represented as a minima on a potential enrgy diagram, where the gradient is zero.

The optimized B-Cl bond length was found to be 1.86A^o and the Cl-B-Cl bond angle was found to be 120 degrees, which is expected as the symmetry was restricted to D_3h, which the is also the ground state symmetry of the molecule. From the literature the B-Cl bond length is 1.75A^o.^[1]. This is the optimized structure as all the frequencies produced were positive. Gaussview does not draw in bonds sometimes even though there is abond present and this is due to certain criteria which governs it, as Gasussview will only draw in a bond when the stregth of the bond between two nuclei falls within a certain range of values. The strength of the bond is related to the distance between the two nuclei concerned,as the further away the nuclei are, the weaker the bond is (as thought of by Gaussian). A bond is defined as an attraction between two atoms or ions but which can flucuate in length and therefore strength, but remains stable as the atoms are still associated with each other. The process of forming/breaking a bond requires an input/output of energy. The optimization calculation took around 14 seconds to complete which is a relatively short amount of time whereas the frequency calculation took 47 seconds. The summary table for the optimization and frequency analysis can be seen below.

Cis and Trans

This section involves the modelling of the cis and trans forms of the complex Mo(CO)₆(PCl₃)₂. The structures will be optimized and then the frequencies will be calculated.

Optimization

Firstly the two structures were drawn in Gaussview and then an optimization calculation was set up and the method used was B3LYP and the basis set used was LANL2MB. "Opt=loose" was also added to the additional keywords section. The resulting structures can be seen below.

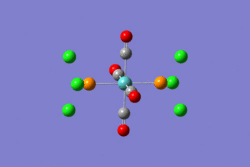output files: cis- (DOI:10042/to-3356 ) trans- (DOI:10042/to-3355 )

From the images it can be seen that after the first optimization Gaussview did not draw in the bonds between Mo and P and P and Cl. This however does not mean that there is no bond there. This approximation was good for bonds lengths and angles but not for the dihedral angles and so the structures needed to be tweaked by changing the torsion angles of the PCl3 groups, as described in the lab tutorial. The structures were then optimized again but using the basis set LANL2DZ and the method B3LYP. The additional keywords "int=ultrafine scf=conver=9" were also added. The fully optimized structures can be seen below.

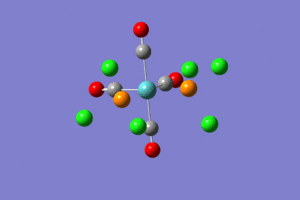output files: cis. https://www.ch.imperial.ac.uk/wiki/index.php/Image:Lo.Log_20885.out trans. https://www.ch.imperial.ac.uk/wiki/index.php/Image:Lo.Log_20884.out

The trans isomer was found to have an energy of -623.576 Hartree which equates to -1637198 KJ/mol. The cis isomer was found to have an energy of -623.577 Hartree which equates to -1637201 KJ/mol. The cis isomer is therefore of a lower energy and can be regarded as the most stable form. The cis form may be lower in energy due to increased backbonding by the carbonyl groups, which is less in the trans form. The difference in energy between the two isomers is 3 KJ/mol. This is a relatively low difference when compared to the overall energies of the ismoers. The overall dipole for the cis form was 1.3 compared with 0.3 for the trans form. The dipole of the trans isomer is lower due to the dipoles of the carbonyl groups cancelling each other out due to them being opposite each other. Even though the cis form is lower in energy when Cl's were used instead of phenyl groups, it would be expected that if the actual molecule modelled had the phenyl groups present then it would be the trans isomer which would be lower in energy due to the lower amount of steric intereations of the phenyl groups.

Comparison of bond lengths
Bond	cis/A^o	trans/A^o	cis-Mo(CO)₄(PPh₃)₂^[2]
Mo-C	2.06	2.06	2.04
Mo-P	2.51	2.44	2.57
P-Cl	2.24	2.24	-
C=O	1.17	1.17	-

The Mo-P bond length is longer in the cis isomer than the trans isomer and this is likely due to steric interactions between the chlorine atoms as in the trans isomer the PCl₃ groups are far aprt from each whereas in the cis case they are adjacent to each other. Only a literature value for the cis isomer could be found and this relates to the original compound with phenyl groups instead of chlorine, which makes the comparison slightly unfair due to the large size difference of the groups. Though it can be seen that when the phenyl groups are present the Mo-P bond length in the cis isomers is larger and this would be the case for the trans isomer as well if a comaprison were to be made.

The P-Mo-P bond angle in the trans isomer is 177 degrees whichis not quite 180. This may be due tothe fact that the PCl3 groups are eclipsed and so slightly repel each other. The C-Mo-C bond angle in the trans isomer was 179.9 degrees compared to 178 degrees in the cis isomer.

Frequency Analysis

The frequencies produced by the frequency analysis were all positive for both the isomers implying that the structures obtained were the fully optimized ones. Some of the frequencies obtained were very low and are shown below.

trans isomer
Vibration form	frequency cm^-1	description
	4.82	rocking
	6.11	rocking

Cis isomer
Vibration form	frequency cm^-1	description
	10.7	rocking
	17.6	rocking

The low frequency vibrations are those occuring due to thermal excitation, as they are not localised and are of low energy.

output files: cis- (DOI:10042/to-3358 ) trans- (DOI:10042/to-3357 )

The IR spectra for the two compounds:

Comparison of carbonyl stretching frequencies:

trans isomer
mode	freq/^cm-1	Intensity
42	1950	1475
43	1951	1466
44	1977	0.7
45	2031	3.8

cis isomer
mode	freq/cm^-1	Intensity
42	1945	762
43	1948	1498
44	1958	632
45	2023	597

From the tables above it can be seen that the frequencies and the intensities at which the vibrations occur differ, with the trans stretches occuring at a higher frequency compared to the corresponding cis mode. Four peaks would be seen in a real IR spectrum for the cis isomer, but only two would be seen for the trans isomer and this sort of shown by the results as two of the vibrations in the trans isomer have very low intensities. This is due to the symmetrical nature of those vibrations.

Mini project: Ammonia Borane

Ammonia Borane has the structure BH₃NH₃. Ammonia borane will be modelled using Gaussview so that its properties can be investigated. Where possible comparisons to ethane will be made due to the similarities in their structures.

Optimization and Conformers of Ammonia Borane

Firstly a molecule of ammonia borane was modelled in Gaussview with no real constraints put on its geometry. An optimization calculation was then performed using the method B3YLP and the more accurate basis set 6-31G,d to find the optimized form of the molecule. The image below shows the resulting structure.

output file: https://www.ch.imperial.ac.uk/wiki/index.php/Image:Lo.AB_OPT_1.LOG

As you can see from the image above the optimized form of ammonia borane is the staggered form. The total energy of the staggered form is -83.2132 a.u which equates to -218476 KJ/mol. This is the fully optimized form as the frequency analysis returned all postive vibrations.

freq. output: https://www.ch.imperial.ac.uk/wiki/index.php/Image:Lo.AB_FREQ_2.LOG

The eclipsed form of ammonia borane was then modelled using Gaussview and this was achieved by taking the optimized staggered form and rotating about the N-B bond until the hydrogens were eclipsed. An energy calculation was then performed on this structure using the same method and basis set as above. An energy calculation had to be done because when an eclipsed form was optimized it would come out as the staggered form.

output file: https://www.ch.imperial.ac.uk/wiki/index.php/Image:Lo.ECLIPSED_AB.LOG

The total energy of the eclipsed conformer is -83.2097 a.u which is equal to -218467 KJ/mol, which is a higher energy when compared to that of the staggered conformer. The staggered conformer is therefore the most stable as it is lower in energy and this is why the initial optimization produced the staggered form of ammonia borane. The difference in energy between the two conformers is 9 KJ/mol and this is the rotational barrier for ammonia borane.

Staggered and Eclipsed conformers of ethane

The staggered and eclipsed conformers of ethane were then modelled in Gaussview and optimized in the same way as the ammonia borane molecules.

staggered output: https://www.ch.imperial.ac.uk/wiki/index.php/Image:Lo.ETHANE_OPT_1.LOG eclipsed output: https://www.ch.imperial.ac.uk/wiki/index.php/Image:Lo.ETHANE_ECLIPSED_2.LOG

The staggered form of ethane is the fully optimized form, as shown by the frequency analysis where all the vibrations were positive.

Optimized staggered ethane freq: https://www.ch.imperial.ac.uk/wiki/index.php/Image:Lo.ETHANE_FREQ_STAG.LOG

The total energy of the staggered ethane conformer is -79.8304 a.u which equals -209594 KJ/mol, whereas the total energy of the eclipsed conformer is -79.8252 a.u which equals -209582 KJ/mol. Therefore, the staggered conformer is lower in energy and the difference in energy between the two conformers is 12 KJ/mol. The reason the staggered form is more stable is due to donation of electron density from a C-H bond into the antibonding orbital of an aligned C-H bond on the opposite methyl group.

The difference between the staggered and eclipsed conformers is greater in ethane than ammonia borane, 12 KJ/mol compared to 9 KJ/mol and this may be due to the C-C bond length (1.53A^o) being shorter than the B-N bond length (1.67A^o) as rotation about the C-C bond will be harder as the hydrogens are closer to each other and therefore more likely to sterically interact. The longer B-N bond allows better rotation about it as the hydrogen atoms are further away from each other. The bond lengths were taken from the optimized structures of the molecules.

All the above was submitted before 5pm on the Tuesday the 8th but everything below that is part of the mini project was added afterwards.

A closer look at the geometry of ammonia borane

The values listed below were taken from the staggered form of ammonia borane as this is the lowest energy configuration.

Bond lengths in ammonia borane
Bond	Length/A^o
B-N	1.67
B-H	1.21
N-H	1.02

The B-H bond length in ammonia borane is slightly larger than the B-H bond length observed in BH₃ (1.19A^o. The N-H bond length is considerably shorter than the B-H bond length and this is because nitrogen is more electronegative than borane and so draws its hydrogens closer to it.

Bond Angles in ammonia borane
Bond	Angle/degrees
H-N-B	111.1
H-B-N	104.5
H-B-H	113.9
H-N-H	107.7

The H-N-B bond angle is greater than the H-B-N bond angle and this could be because the B-H bond length is slightly larger. The H-B-H bond angle is halfway between a tetrahedral angle of 109.5 degrees and the bond angle of 120 degrees found in trigonal planar BH₃. The H-N-H bond angle is very close to the angle of 107 degrees found in ammonia as in principle the B-N bond acts in a similar way to the lone pair of nitorgen in ammonia in terms of repeling the N-H bonds. The H-N-H bond is slightly larger than the angle found in ammonia because the electron density is shared between the boron and the nitrogen in ammonia borane and not centred over the nitrogen is it is in ammonia.

Bonding in ammonia borane and ethane

The Molecular orbitals of ammonia borane were computed using the method B3LYP and the basis set 6-31G,d. In the additional keywords section "pop=full" was added so that the MO's would be calculated. Under the NBO tab "Full NBO" was selected.

MO 1
MO 2
MO 3
MO 4
MO 5
MO 6
MO 7
MO 8
MO 9
MO 10
MO 11
MO 12
MO 13
MO 14

output file: https://www.ch.imperial.ac.uk/wiki/index.php/Image:Lo.AB_POP_1.LOG

The molecular orbitals of ethane were also computed using the same criteria as for ammonia borane.

MO 1
MO 2
MO 3
MO 4
MO 5
MO 6
MO 7
MO 8
MO 9
MO 10
MO 11
MO 12
MO 13
MO 14

output file: https://www.ch.imperial.ac.uk/wiki/index.php/Image:LO_ETHANE_POP.LOG

From observing the molecular orbitals the main difference seems that the orbitals of ethane are more symmetrical about the central bond than those of ammonia borane and this is expected because ammonia borane contains two different atoms which possess different electronegativities and this therefore will scew the electron density. In ammonia borane most of the electron density is located over the borane atom and this is beacuse the N-B is a dative bond as the nitrogen donates its lone pair of electrons into an empty p orbital of the borane and so the electrons reside closer to the borane atom, even though nitrogen is more electronegative. In ethane the electron density shared between the two carbon atoms is equal as there is just a normal covalent bond between them.

NBO Analysis of Ammonia Borane and Ethane

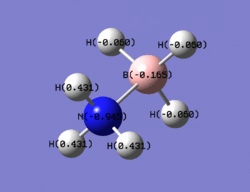The images above help to show the charge distribution over the two different molecules. The charge distribution over ethane is symmetrical and even whereas it is not in ammonia borane. What is interesting to note is how the hydrogens bonded to the borane atom have a very similar charge to the borane whereas the hydrogens bonded to the nitrogen have very different charges to the nitrogen and this is again due to the electronegativity of the nitrogen atom. From the previous study of BH₃ it cane seen how the donation of the nitrogen lone pair into an empty p orbital on the borane atom has changed its charge, as it has become more negative.

In order to understand why ammonia borane has a high melting point and is therefore a solid at room temperature you would need to model more than one molecule and so looking at bulk ammonia borane would be best, as it is the intermolecular forces you are wanting to study. The only evidence from the calculations done during this investigation which can give an idea of why ammonia borane has a high melting point when compared to ethane is if the dipole moments are looked at. From the original optimization of ammonia borane the dipole moment was 5.6 wheras the dipole moment of modelled ethane molecule was zero. Due to ammonia borane having a high dipole moment the intermolecular attractions between ammonia borane molecules are greater and this can help to explain why ammonia borane has a high melting point of 110 ^oC. Ethane has a low melting point because it has weak intermolecular interactions as it only possesses van der waals interactions which are weaker in the case of ethane because it is a small molecule.

Conclusion

The similarities and differnces between the two molecules ammonia borane and ethane have been addressed. The main similarity being that they both prefer a staggered geeometry and the main difference being how they bond.

References

↑ M. Atoji and W. N. Lipscomb – B-Cl Distance in Boron Trichloride - J. Chem. Phys. 27, 195 (1957)
↑ D. J. Darensbourg, R. L. Kump, Inorg. Chem., 1978, 17, 2680-2682. DOI:10.1021/ic50187a062

[1] M. Atoji and W. N. Lipscomb – B-Cl Distance in Boron Trichloride - J. Chem. Phys. 27, 195 (1957)

[ic50187a062-2] D. J. Darensbourg, R. L. Kump, Inorg. Chem., 1978, 17, 2680-2682. DOI:10.1021/ic50187a062

[1]

[2]