Rep:Module2:Dima1407

TlBr3 optimisation

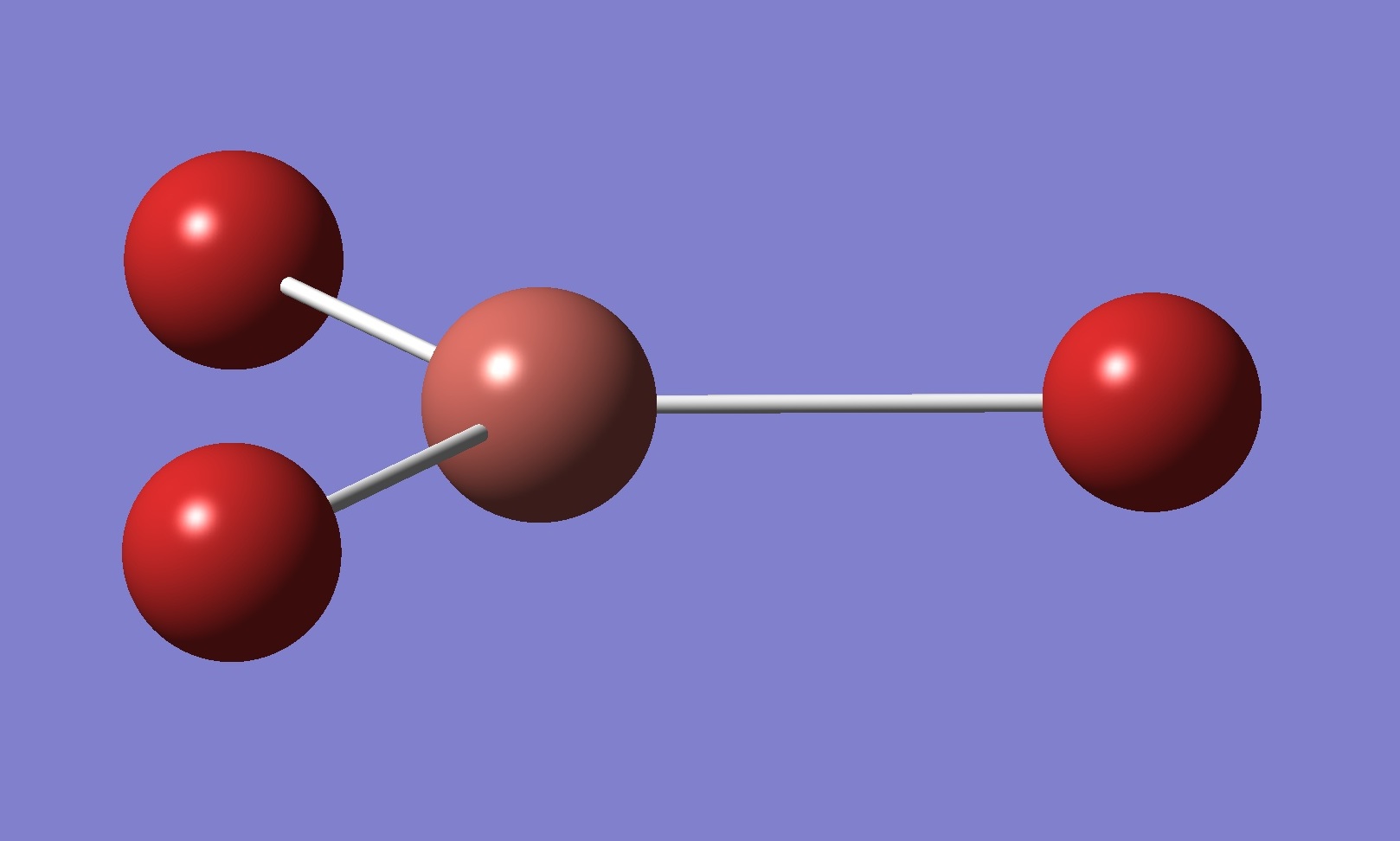
Bond length = 2.65 angstroms

Angle = 120,0 degrees

TlBr3 optimisation file

Molecular Orbitals and Vibrations of BH3

Completed population analysis for BH₃ - DOI:10042/to-5800

Vibrations

No.	Form of vibration	frequency	intencity	symmetry D3h point group		No.	Form of vibration	frequency	intencity	symmetry D3h point group
1	Vibration	1150	93	A2"		4	Vibration	2590	0	A1'
2	Vibration	1200	12	E'		5	Vibration	2730	104	E'
3	Vibration	1200	12	E'		6	Vibration	2730	104	E'

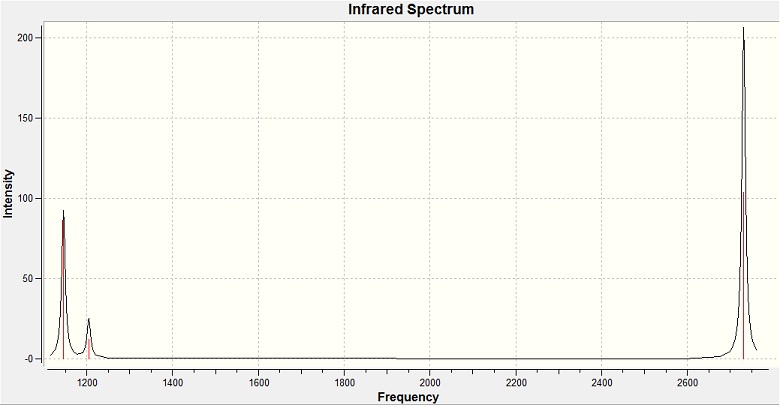
In our IR we have 3 peaks instead of 6. It is due to 2 peaks correspond to double degenerate vibration energy levels and intensity of fourth peak is 0, so we can't see it.

Calculations on TlBr3

Calculation method - RB3LYP

Basis set - LANL2DZ

We have to use the same method and basis set for both calculations because we want to do frequency analysis for a certain calculation we used. So if we used one method and basis set - we should use the same once in frequency analysis.

Because gradient could be zero in case of a maximum as well as in case of minimum, we need an additional test - frequency analysis, which is actually second derivative of potential energy surface.

Log file info

Low frequencies	-3.4226	-0.0026	-0.0004	0.0015	3.9361	3.9361
Low frequencies	46.4288	46.4291	52.1449	165.2685	210.6948	210.6949

As we can see all normal mode vibrations are positive, so optimised molecula is in the ground state (in its lowest energy level)

Vibrations

Frequencies	46 cm-1	46 cm-1	52 cm-1	170 cm-1	210 cm-1	210 cm-1
Intensity	4	4	6	0	25	25

Tl-Br bond length calculated with Gaussian is 2.65 angstroms, which is in a quite good agreement with literature value - 2.52.

GaussViw uses average bond length for all structures. So for example the bond length for PtCl₂ and PtCl₄ is the same. Sometimes when bond is bigger than an average bond, GaussiView does not draw in the bonds where we expect.

The MO diagram of BH₃

	"real" MO	"LCAO" MO
LUMO
HOMO
HOMO-1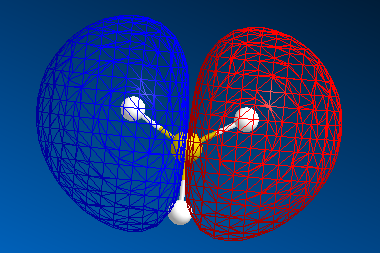
HOMO-2

As we can see from the table the difference between "real" and "LCAO" MOs is quantitative - "real" MO can tell us energy and exact shape. But if we need relative energy levels and approximative shapes - LCAO is much better due to its simplicity.

Isomers of Mo(CO)₄L₂

Optimised trans-isomer of Mo(CO)₄(PCl₃)₂ - DOI:10042/to-5928

Optimised cis-isomer of Mo(CO)₄(PCl₃)₂ - DOI:10042/to-6107

IR vibration table of cis isomer DOI:10042/to-6110

Vibration	Vibration	Vibration	Vibration	Vibration	Vibration
Calculated values	freq. = 483cm-1, Intens. = 251	freq. = 1938cm-1, Intens. = 1605	freq. = 1942cm-1, Intens. = 813	freq. = 1952cm-1, Intens. = 588	freq. = 2019cm-1, Intens. = 545
Literature value		1986cm-1	2004cm-1	2004cm-1	2072cm-1

IR vibration table of trans isomer DOI:10042/to-6111

Vibration	Vibration	Vibration	Vibration
Calculated value	freq. = 435cm-1, Intens. = 801	freq. = 1940cm-1, Intens. = 1606	freq. = 1940cm-1, Intens. = 1606
Literature value		1986cm-1	1986cm-1

Bond length

Bond	Mo-P trans	Mo-P cis	Mo-C trans	Mo-C cis1	Mo-C cis12	C-O
Calculated value, trans	2.42 ang.	2.48 ang.	2.06 ang.	2.05 ang.	2.02 ang.	1.17 ang.
Literature value	2.49* ang.	2.49* ang.	2.02-2.06 ang.	1.98 ang.	2.02 ang	1.15 ang.

The total energy of the cis- and trans-isomer are -623.69291203 a.u. and -623.69415610 a.u. The energy difference is 0.00124407 a.u. or 3.3 kJ/mol. Trans-isomer is more stable because bulky PCl₃ groups are surrounded by small CO groups, but in case of cis-isomer two bulky PCl₃ groups are near each other and this causes repulsion, which effects angles between the bonds (increase bending energy). Trans-isomer is also destabilized due to one P-Cl in PCl₃ is eclipsed with C=O bond which causes angle C-Mo-P to differ from 90 degrees (), that is why energy difference etween two isomers are so small.

Doing our frequency test we did not get any negative values for both isomers, so we get ground state structures. Comparing carbonyl stretches obtained from the GaussView and found in literature we can say that values we have get are very close.

Also we have good results for bond lengths comparing to the literature values, so we can assume that our method is good and GaussView could be used for studding such a structures.

Mini-project: Complex compounds geometry

Complex compound with coordination number 4 could have 2 different geometries: square planar and tetrahedral. We are going to investigate using GaussView which one will Be lover In energy for Pt(NH₃)Cl₂ and Co(NH₃)Cl₂.

Completed optimisation for Pt(NH₃)Cl₂ - DOI:10042/to-6143

Completed optimisation for Co(NH₃)Cl₂ - DOI:10042/to-6142

Pt(NH₃)Cl₂ has a square planar structure which is as predicted for Pt compounds with d⁸ electron structure. Trans isomer is more stable due to its symmetry, but difference is negligible. Co complex has tetrahedral geometry

Ion such As [Ni(CN)₅]^3- could have 2 geometric isomers: square pyramidal and trigonal bipyramidal. As we can see from the optimised files square pyramidal structure is more stable which is in accord with literature.

Bond length

Compound	Ni-C	Ni-C	Ni-C	C-O
Square pyr.	1.87	1.90	1.83	1.19
Trigonal bipyr.	2.06	2.06	2.06	1.15
Lit. sq. pyr.	1.86	2.17	1.86
Lit. tr. bipyr.	1.91	1.99	1.84

Completed optimisation for Square pyramidal - DOI:10042/to-6145

Completed optimisation for trigonal bipyramidal - DOI:10042/to-6144

From two examples we have viewed it is clear that GaussView is very powerful program to predict the geometry and MO for Complex compounds.