Rep:Module2:AYKLeung

Chemistry Computational Lab (Yr3)

Module 2: (inorganic) Molecular Modelling (Structures and Spectroscopy)

Gaussview 3 was used in all modelling exercises

BH₃molecule analysis

Optimisation

BH₃ Optimisation summary

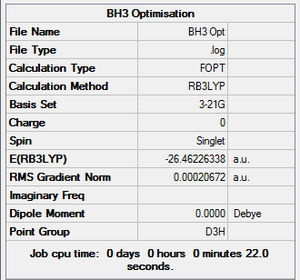
Using Gaussview5.0, a BH3 molecule was created and optimized under the calculation type FOPT, method = RB3LYP and basis = 3.21G. Final energy was found to be – Hartree a.u., and dipole moment = 0.00 Debye. B-H bond length was 1.18 Angstroms. H-B-H bond angle = 120^o. The point group of BH3 is D3H. The summary table is shown on the right.

BH₃total energy vs Opt Step

BH₃RMS vs Opt Step

The total energy and RMS gradient VS calculation steps graphs could be viewed after the optimization. From the .log file where the results were shown, and the fact that the RMS value almost reaching zero (=0.00 ), it could be assumed that the lowest energy geometry was obtained by the software. The RMS represents the derevative of the energy with respect to the spatial separation between the atoms, which becomes 0 when the molecule reaches the optimal geometry.

The molecule could be viewed below:

NBO analysis

BH₃ charge distribution

The NBO analysis looks at the charge distribution of the molecule and the respective molecular orbitals. The overall charge of the molecule is zero according to the .log file, as expected because of the symmetry of the molecule. The 3 H atoms provide complete s contribution, while the B atom has 33.3% s-contribution and 66.6% p-contribution. This shows the boron is sp3 hybridised in terms of the VSEPR model. The charge distribution shows that electron pair between the B-H bonds are likely to be closer to the Boron atom than the Hydrogen atom. So the borane molecule have partial positive charges on Hydrogen atoms and partial negative charge on the Boron atom.

Molecular Orbitals

According to the Mulliken Population Analysis, the molecular orbital’s of BH3 were computed and the results were compared against orbitals predicted using the linear combination of atomic orbital (LCAO) method. Results are shown below.

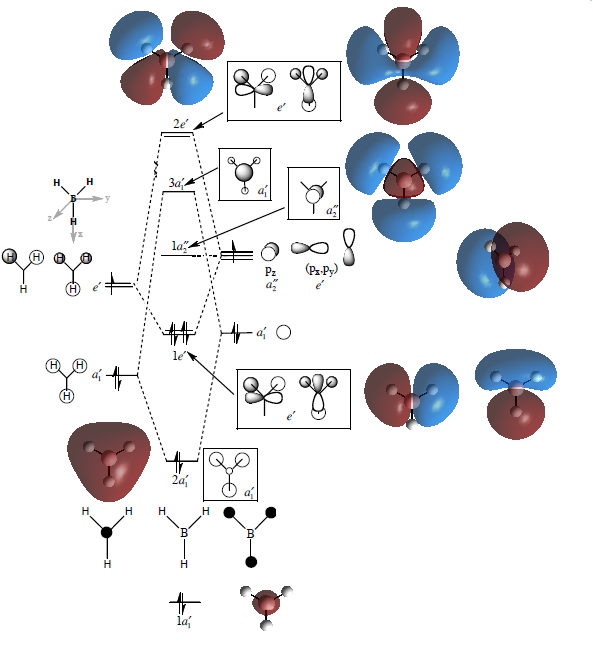
The predictions agree well, which shows that the qualitative prediction is reliable in determining the shape of the orbitals, but not the energies. The quantitative information does not include data regarding the energies. E.g. it is not shown whether the 2e’ or 3a1’ orbitals have the lower energies. This has to be confirmed by running a computational calculation. So in BH3, the 3a1’ orbital is lying 4 kJ mol-1 higher than the 2e’ orbital.

Vibrational analysis

BH3 is a non-linear molecule, and it is expected to have 3N-6=6 vibration modes (N=4). The results match the predictions, where 6 vibration modes were found. Therefore 6 peaks should be expected in the IR spectrum of BH3, whereas only 3 peaks were only found. This is because there are 2 sets of degenerate vibrations at 1210cm-1 and 2175cm-1 and one vibration IR inactive (since there is no change in the dipole moment due to the symmetry of the borane molecule from the a1’ symmetric stretching). Comparing the literature and the computational values errors could be found (largest ~ 4.3% at 2715cm-1). The calculations should be used for identification of the number of vibration, but not for the exact numerical value of the vibrations.

Table 1: Vibrational Frequencies of BH₃

Mode	Calculated Frequency (cm-1)	Vibration	Literature Frequency (cm-1)	Vibration description	Symmetry Point Group
1	1144.15		1148	Boron atom stationary, with Hydrogen atoms moving in sync in and out of plane, wagging	A2
2	1144.15		1197	Boron and a Hydrogen atom stationary, with the other two hydrogen atoms bending along plane	E'
3	1144.15		1197	Boron atom stationary, with all three Hydrogen atoms bending	E'
4	1144.15		2502	Boron atom stationary, whilst all three Hydrogen atoms stretching in sync, on the same plane	A1
5	1144.15		2602	Boron and a Hydrogen stationary, with other two Hydrogen atoms stretching out of sync	E'
6	1144.15		2602	Boron atom stationary, whilst all three Hydrogen atoms stretching, where one of them is out of sync	E'

Part 2: TlBr3 analysis

Optimisation

TlBr₃ Summary Table

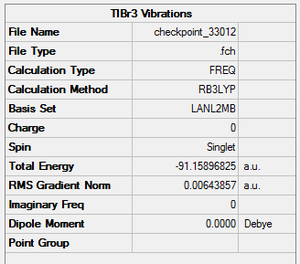
A similar optimization was carried out for TlBr3, with the same method as BH3, FOPT & RB3LYP, but with a medium-level basis set, LanL2DZ, to provide a more accurate optimization. The final energy was found to be -91.1589 Hartree a.u. and the dipole moment was 0.00 Debye (as expected from the symmetry of the compound). The Tl-Br bond length was 2.65 Angstroms, and the Br-Tl-Br angle was 120^o. Both values agrees with the literature value (2.55 Angstroms and 120^o). The point group was D3H. The summary table is shown on the right.

This job is published on D-Space: http://hdl.handle.net/10042/to-5905

Vibrational Analysis

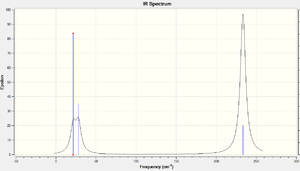
The vibrational analysis was computed and results are shown below. The calculated IR spectrum is shown on the right. Similar to the spectrum obtained for BH₃, there are only 3 visible peaks - but there are 6 vibration modes! This is because of the 2 sets of degenerate modes and a vibration that is IR inactive.

IR Spectrum of TlBr₃

Table 2: Vibrational Frequencies of TlBr₃

Mode	Calculated Frequency (cm-1)	Vibration	Literature Frequency (cm-1)	Vibration description	Symmetry Point Group
1	21.65		5.4401	Tl atom stationary, with Cl atoms moving in sync in and out of plane	A2
2	28.17		2.9816	Tl and a Cl atom stationary, with the other two Cl atoms bending along plane	E'
3	28.17		2.9817	Tl atom stationary, with all three Cl atoms bending	E'
4	172.90		0.0000	Tl atom stationary, whilst all three Cl atoms stretching in sync, on the same plane	A1
5	233.41		14.0436	Tl and a Cl atom stationary, with other two Cl atoms stretching out of sync	E'
6	233.41		14.0445	Tl atom stationary, whilst all three Cl atoms stretching, where one of them is out of sync	E'

Lost bond in Gaussview

Different Types of Chemical Bonds

During the optimization, Gaussview 5.0 sometimes excludes the bons between the atoms, but this does not mean there is no bonding interactions in between. The bonds do not appear because the interactions are not large enough to be considered as any specified bond lengths in the database, so the Gaussview does not recognize and thus could not show them in the model. This happens exclusively for inorganic compounds, since bond lengths in the database are largely based on organic molecules.

Chemical Bond

A chemical bond could be viewed as an attraction force between two or more atoms, which lowers the energy of the compound. There 3 examples of typical strong bonds,:electromagnetic interactions between positively-charged nuclei sharing negatively-charged electrons in a covalent bond; or electrostatic interactions between a positive cation and a negative anion as an ionic bond; or electrostatic interactions between positive metallic cations with a sea of electrons forming metallic bonds. Common weak bonds include: electrostatic attraction between dipoles such as hydrogen bonding and induced dipole interactions (Van der Waals forces).

Mo(CO)₄(PCl₃)₂ cis- and trans- isomers analysis

Mo(CO)₄(PCl₃)₂ has cis and trans isomer. The most significant vibration bands are the CO stretching. This is relative to the symmetry of the compound: cis would have for active whilst trans would only have one. Vibrations of both of these isomers are investigated below.

Optimisation

Summary table for cis-Mo(CO)₄(PCl₃)₂

Summary table for trans-Mo(CO)₄(PCl₃)₂

Two optimisations were carried out in this experiment. First we used DFT-B3LYP method under the basis set of LanL2MB, with additional comments: "opt=loose". Turns out the trans-isomer reached minimum energy when the PCl3 groups are in a staggered conformation, whereas the cis-isomer does not show any particular symmetry. The P-Cl bonds disappeared, probably due to the reasons discussed above. A second optimisation was carried out using the primarily optimised structures.This time the basis set was changed to LanL2DZ. The LanL2DZ uses more functions than LanL2MB which produces more accurate results. The summary tables for the optimised compounds are shown on the right. Comparing the 2 optimisations, the second optimisation produces lower energies for both isomers. This is because the system might have more than one energy minima and the calculations might take false assumptions, which leads to a very low value of RMS convergence gradient. The initial structure of the isomers are therefore very important.

Frequency and Vibration

The frequency calculations are carried out using the doubly optimised log files, with the same method and basis set. The numerical structure of the compounds are shown below. (cis-Mo(CO)₄(PCl₃)₂ could not be found, therefore values from Cr(CO)₄(PCl₃)₂ was taken instead, under the assumption that they are similar in reactivity, since they belong to the same group)

Table 3: Experimental and literature values of cis- and trans- Mo isomers

Isomer	Mo-C Length(Angstoms)	Mo-P Length(Angstoms)	P-Mo-P angle (o)	C-Mo-P angle (o)
Cis-Mo(CO)4(PCl3)2	2.012	2.512	94.168	(cis-) 89.4 (trans-) 176.08
Lit Cis-Mo(CO)4(PCl3)2	2.04	2.58	104.6	(cis-) 80.6 (trans-) 163.7
Trans-Mo(CO)4(PCl3)2	2.043	2.403	177.38	89.98
Lit Trans-Mo(CO)4(PCl3)2	1.87	2.36	176.7	89.5

The experimental bond lengths are similar to the literature values as shown above, proving that the calculations provides good predictions of reality. But the bonds angles do not agree very well. This is because of the difference in the P-R group. R = Cl in our experiment, but R = Ph in the literature values, which is much bigger. Therefore steric effects have to be taken into account. But since the shape of the molecule is generally within the prediction range, it could be viewed as a successful prediction of the structure.

The cis-isomer is in the C_2v symmetry point group, whereas the trans-isomer belongs to the D_4h point group.

The energies obtained for both isomers are very similar, with the trans- isomer slightly lower in energy by 0.0112 Hartree a.u., which is equivalent to 3.3 kJ/mol-1. This could be explained by the steric repulsion by the bulky PCl₃ groups in the cis-isomer, where in the trans-isomer they are separated very far apart.

Cis-isomer vibration calculations submitted to D-space: http://hdl.handle.net/10042/to-5926

Trans-isomer vibration calculations submitted to D-space: http://hdl.handle.net/10042/to-5927

IR Spectrum of Cis-isomer

IR spectrum of Trans-isomer

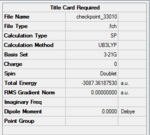
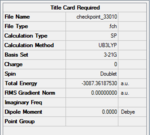
The table below shows the frequencies of C=O stretchings for both isomers. Once again the experimental and literature values might differ mre than expected because the PR₃ are different:

Table 4: Frequencies of C=O stretchings

Cis-Mo(CO)4(PCl3)2
Calculated Vibration Frequency cm-1	Calculated Intensity	Experimental Vibration Frequency cm-1	Point group symmetry
1945.34	763.132	1986	B2
1948.68	1498.15	1994	B1
1958.39	632.558	2004	A1
2023.33	597.833	2072	A1
Trans-Mo(CO)4(PCl3)2
1992.21	1524.95	1896	Eu
1992.62	1516.19	1896	Eu
2020.58	0.3848	N/A	B1g
2075.05	3.6488	N/A	A1g

The results do agree with each other very well. This might be due to the fact that the PR₃ does not play a large part in the C=O stretching vibrations.

Mini-Project: Investigating PX₆^- and AsX₆^- species, X = F, Cl, Br

The molecular structures of PX₆^- and AsX₆^- were looked at extensively in our first and second years. Their VSEPR models and in main group chemistry. In this part we will concentrate on looking at the vibration modes of these octahedral compounds.

Optimisation

Similar to previous optimisations, a method of DFT, RB3LYP was used, and basis set was 3-21G. The summary tables and jmol's are shown below.

Table 5: Summary tables and Molecule Models for PX₆^- and AsX₆^-

PF6-	PCl6-	PBr6-	AsF6-	AsCl6-	AsBr6-

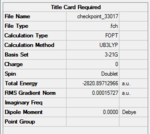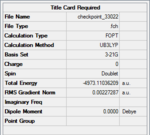The energies and bond lengths of the species are shown below.

Table 6: Optimised values for PX₆^- and AsX₆^-

Species	PF6-	PCl6-	PBr6-	AsF6-	AsCl6-	AsBr6-
Energy (Hartree a.u.)	-935.3	-3087	-3087	-2821	-4973	-17600
Energy kJ mol-1	-2.456e+6	-8.105e+6	-8.105e+6	-7.407e+6	-1.306e+7	-4.621e+7
Bond length (Angstoms)	1.631	2.040	2.519	1.757	2.382	2.561

The energies of the species demonstrate interesting behaviours. The fluoride compounds are significantly higher in energy than the other compounds. This could be explained by the fact that the fluoride bonds are very short and for steric reasons increasing the energy of the compound as a whole. The Phosphorous and Arsenic compounds do not show the same trend. This might be because of the sizes of the central atoms which influences the steric space in between the X compounds. Therefore PCl₆^- and PBr₆^- have similar energies, whereas AsCl₆^- and AsBr₆^- have a much larger energy difference.

Vibration

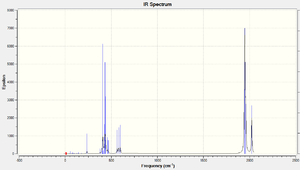
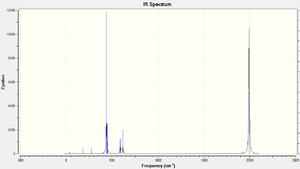
There are 15 vibration modes for all compounds, which is expected according to the 3N-6 rule for non-linear compounds. The IR spectra for PF₆^- and PCl₆^- are shown on the right. There are errors found with larger compounds and therefore other spectra were not included. View results on D-Space: PF₆^-: DOI:10042/to-6095 , PCl₆^-:

PF₆^- IR Spectrum

PCl₆^- IR Spectrum

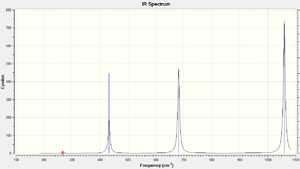
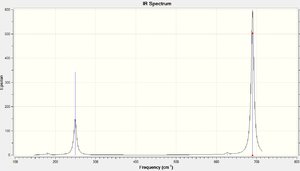
As this is an Octahedral compound a lot of vibrations were found to be degenerate, thus there are less peaks than expected on the spectra.

Table 7: Vibrations of PF₆^- and PCl₆^-

Mode number	PF6- Frequencies (cm-1)	PF6- calculated intensity	PCl6- Frequencies (cm-1)	PCl6- calculated intensity
1	208.59	0.000	169.8	0.000
2	267.32	0.605	180.6	0.9208
3	267.32	0.605	180.6	0.9208
4	276.23	0.000	186.4	16.31
5	324.48	70.785	186.4	16.31
6	324.48	70.785	204.53	0.000
7	390.73	0.000	249.2	42.80
8	390.73	0.000	284.81	0.000
9	432.27	54.16	284.8	0.000
10	531.19	0.000	421.1	0.000
11	655.34	0.000	437.9	0.000
12	681.42	68.883	536.9	0.000
13	681.42	68.883	626.9	1.191
14	732.62	0.000	626.9	1.191
15	1059.23	214.69	689.90	173.3

Surprisingly it is calculated that a smaller molecule produces peaks at higher frequencies, which is unexpected because usually a larger molecule would produce a larger energy.

Conclusion

Gaussview5.0 predicts the shape of the molecule quite well, given that the optimisation method and basis set were correctly assigned. The vibrations were also well predicted for some molecules, but has limitations for large molecules or special bondlengths, as the database does not register everything that has to be calculated. Overall Gaussview5.0 and Gaussian9 are powerful tool when predicting the shapes, energies and other properties of molecules.